- \(10^{10}\)を\(2020\)で割った余りを求めよ。
- \(100\)桁の正の整数で各位の数の和が\(2\)となるもののうち,\(2020\)で割り切れるものの個数を求めよ。
(一橋大)
解答
\(2020\)を法として考える.以下,\(\mod 2020\)を省略して記述する.
\(10000\equiv10000+2020\cdot(-5)\equiv-100\)であるから,
\begin{align*}
10^{10}\equiv&10^2\cdot(10^4)^2\\
\equiv &10^2\cdot(-100)^2\\
\equiv &10^2\cdot10000\\
\equiv &10^2\cdot(-100)\\
\equiv &-10000\\
\equiv &-(-100)\\
\equiv &100
\end{align*}
ゆえに\(10^{10}\equiv100\)(\(1.\)の答え)
\(100\)桁の正の整数で各位の数の和が\(2\)であるような数は
\begin{align*}
\mathrm{(i)}\quad &2\underbrace{0\cdots0}_{99\text{個}}=2\times10^{99}\\
\mathrm{(ii)}\quad &1\underbrace{0\cdots01\overbrace{0\cdots0}^{k\text{個}}}_{99\text{個}}=10^{99}+10^k\quad(0\leq k \leq 98)
\end{align*}のいずれかである.
\(\mathrm{(i)}\)のとき
\(1.\)により\(10^{10}\equiv10^2\)であることに注意して,
\begin{align*}
2\times10^{99}\equiv&2\cdot10^{9}\cdot(10^{10})^9\\
\equiv&2\cdot10^{9}\cdot(10^{2})^9\\
\equiv&2\cdot 10^{27}\\
\equiv&2\cdot(10^{10})^2\cdot10^7\\
\equiv&2\cdot(10^{2})^2\cdot10^7\\
\equiv&2\cdot10^{11}\\
\equiv&2\cdot10^{10}\cdot10\\
\equiv&2\cdot10^{2}\cdot10\\
\equiv&2000\\
\end{align*}ゆえにこの数は\(2020\)で割り切れない.
\(\mathrm{(ii)}\)のとき
\(10^{99}+10^{k}\equiv 1000 + 10^{k}\)より(なぜならば\(\mathrm{(i)}\)の途中過程により\(10^{99}\equiv1000\)),\(1000+10^k\equiv 0(\Leftrightarrow 10^{k}\equiv -1000)\)を満たす\(k~(0\leq k \leq 98)\)の個数を調べればよい.\(k\)の値は高々\(99\)個なので,実際に調べてみると(やる気),
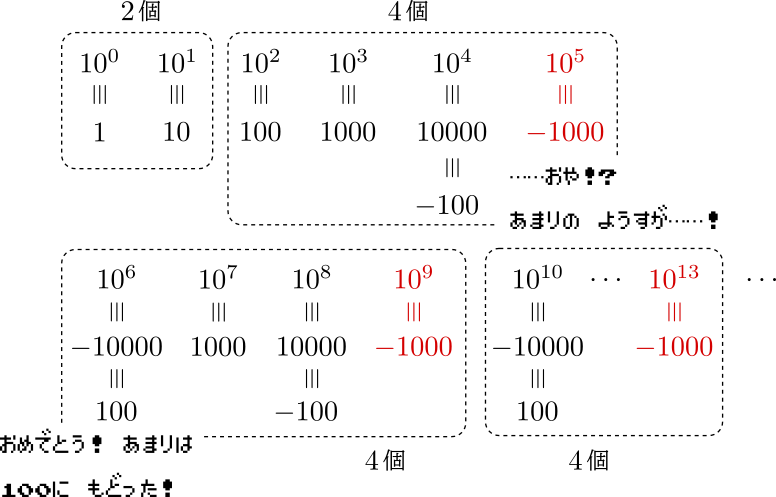
\(1,10\)から始まり,\(100,1000,-100,-1000\)と繰り返すことがわかる.したがって,\(99=2+4\times 24+1\)により求める個数は\(24\)個とわかる.(\(2.\)の答え)
解答終

