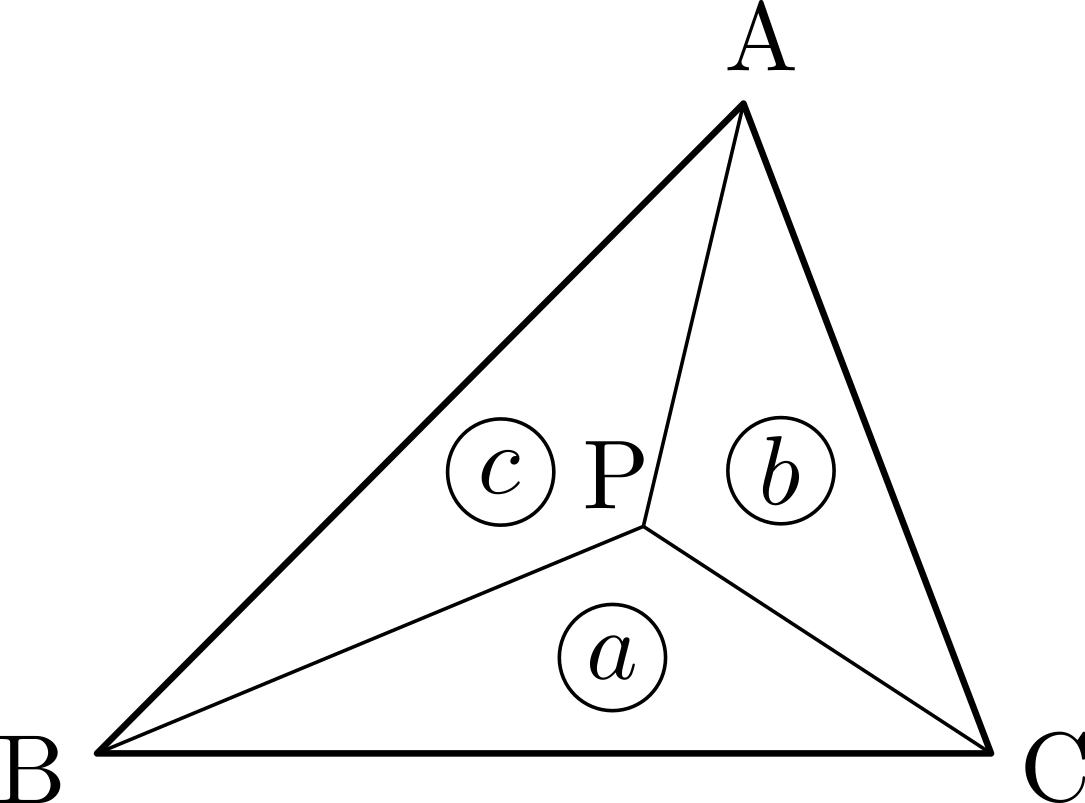
 \(\triangle{\mathrm{ABC}}\)において,\(\triangle{\mathrm{PBC}}:\triangle{\mathrm{PCA}}:\triangle{\mathrm{PAB}}=a:b:c~\)のとき,\[\overrightarrow{\mathrm{AP}}=\frac{1}{a+b+c}(b\overrightarrow{\mathrm{AB}}+c\overrightarrow{\mathrm{AC}})\]
\(\triangle{\mathrm{ABC}}\)において,\(\triangle{\mathrm{PBC}}:\triangle{\mathrm{PCA}}:\triangle{\mathrm{PAB}}=a:b:c~\)のとき,\[\overrightarrow{\mathrm{AP}}=\frac{1}{a+b+c}(b\overrightarrow{\mathrm{AB}}+c\overrightarrow{\mathrm{AC}})\]
証明
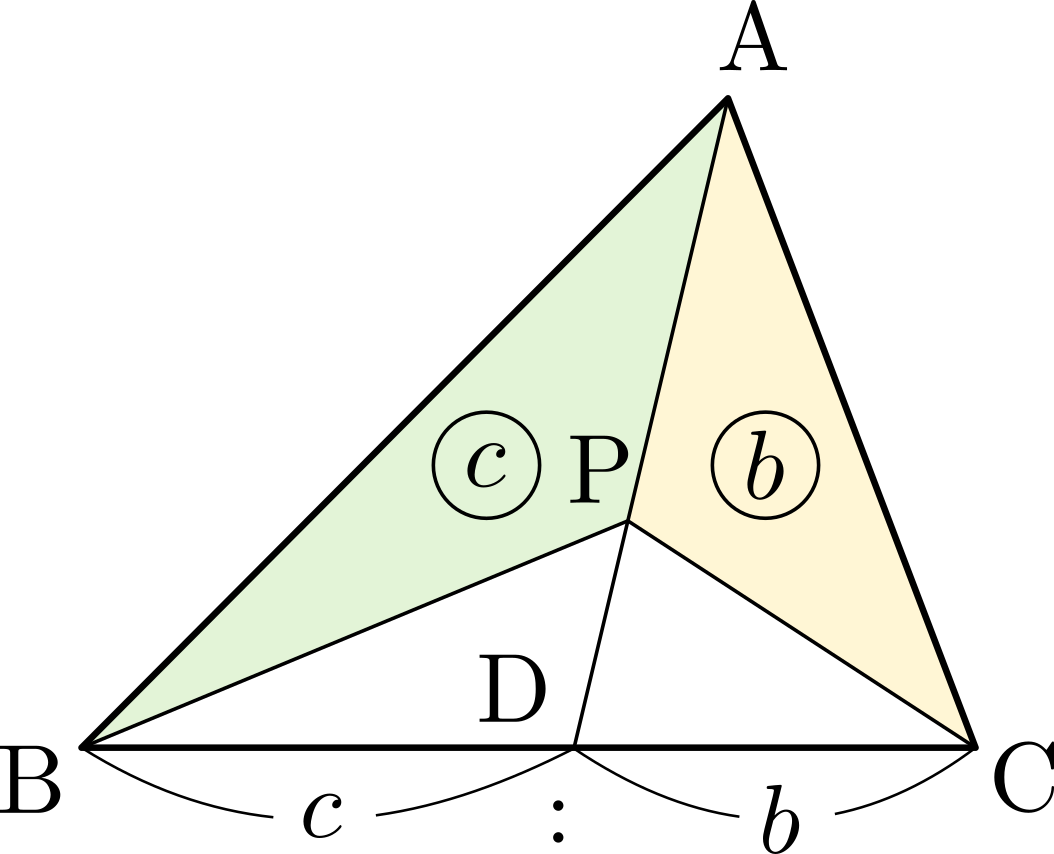 直線\(\mathrm{AP}\)と辺\(\mathrm{BC}\)との交点を\(\mathrm{D}\)とおくと,\(\triangle{\mathrm{PCA}}:\triangle{\mathrm{PAB}}=b:c\)より\(\mathrm{BD}:\mathrm{DC}=c:b\)であるから,内分の公式により\[\overrightarrow{\mathrm{AD}}=\frac{b\overrightarrow{\mathrm{AB}}+c\overrightarrow{\mathrm{AC}}}{c+b}\]
直線\(\mathrm{AP}\)と辺\(\mathrm{BC}\)との交点を\(\mathrm{D}\)とおくと,\(\triangle{\mathrm{PCA}}:\triangle{\mathrm{PAB}}=b:c\)より\(\mathrm{BD}:\mathrm{DC}=c:b\)であるから,内分の公式により\[\overrightarrow{\mathrm{AD}}=\frac{b\overrightarrow{\mathrm{AB}}+c\overrightarrow{\mathrm{AC}}}{c+b}\]
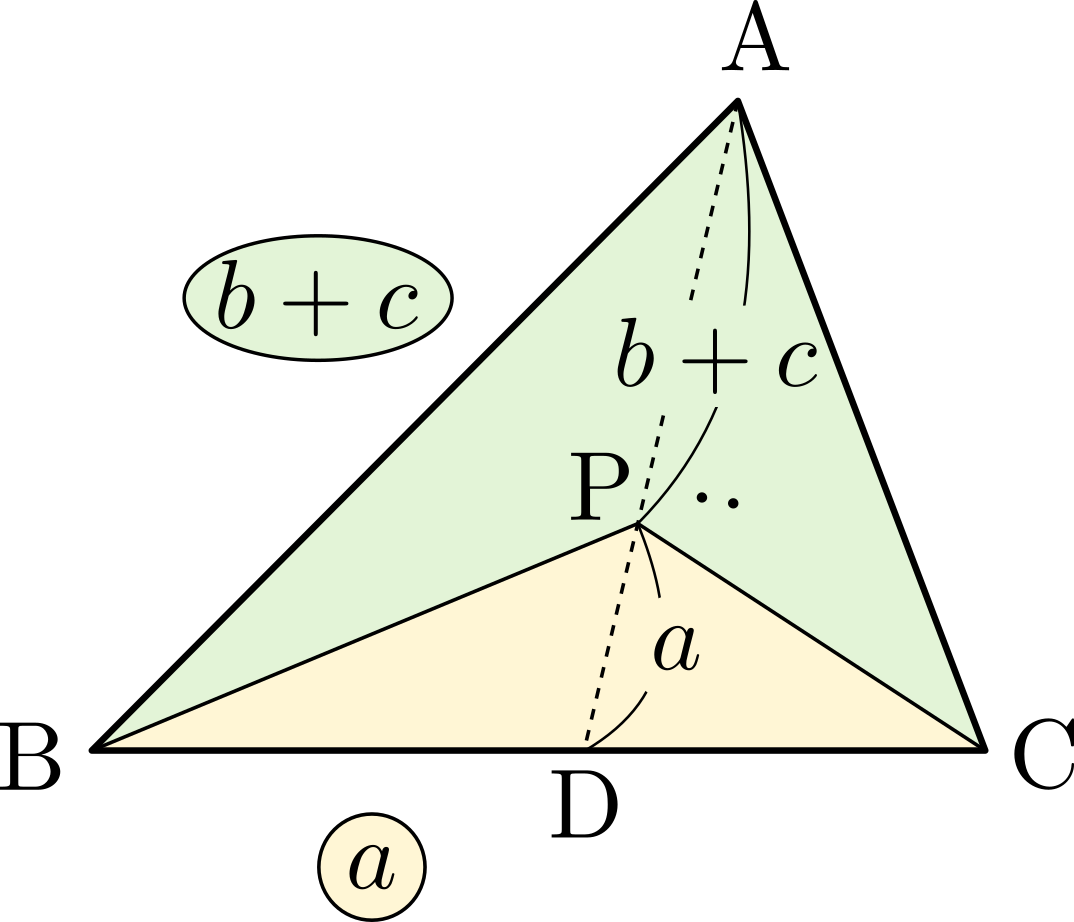 また,凹四角形\(\mathrm{ABPC}\)と\(\triangle{\mathrm{PBC}}\)の面積比が\(b+c:a\)であることから\(\mathrm{AP}:\mathrm{PD}=b+c:a\)だから\[\overrightarrow{\mathrm{AP}}=\frac{b+c}{a+b+c}\overrightarrow{\mathrm{AD}}\]
また,凹四角形\(\mathrm{ABPC}\)と\(\triangle{\mathrm{PBC}}\)の面積比が\(b+c:a\)であることから\(\mathrm{AP}:\mathrm{PD}=b+c:a\)だから\[\overrightarrow{\mathrm{AP}}=\frac{b+c}{a+b+c}\overrightarrow{\mathrm{AD}}\]
この\(2\)式により
\begin{align*}
\overrightarrow{\mathrm{AP}}=&\frac{b+c}{a+b+c}\overrightarrow{\mathrm{AD}}\\
=&\frac{b+c}{a+b+c}\frac{1}{b+c}(b\overrightarrow{\mathrm{AB}}+c\overrightarrow{\mathrm{AC}})\\
=&\frac{1}{a+b+c}(b\overrightarrow{\mathrm{AB}}+c\overrightarrow{\mathrm{AC}})
\end{align*}
証明終
幾何の問題でおなじみ「底辺が等しければ面積比=高さの比」を利用します。この公式は例のあの問題で役立ちます:
解答
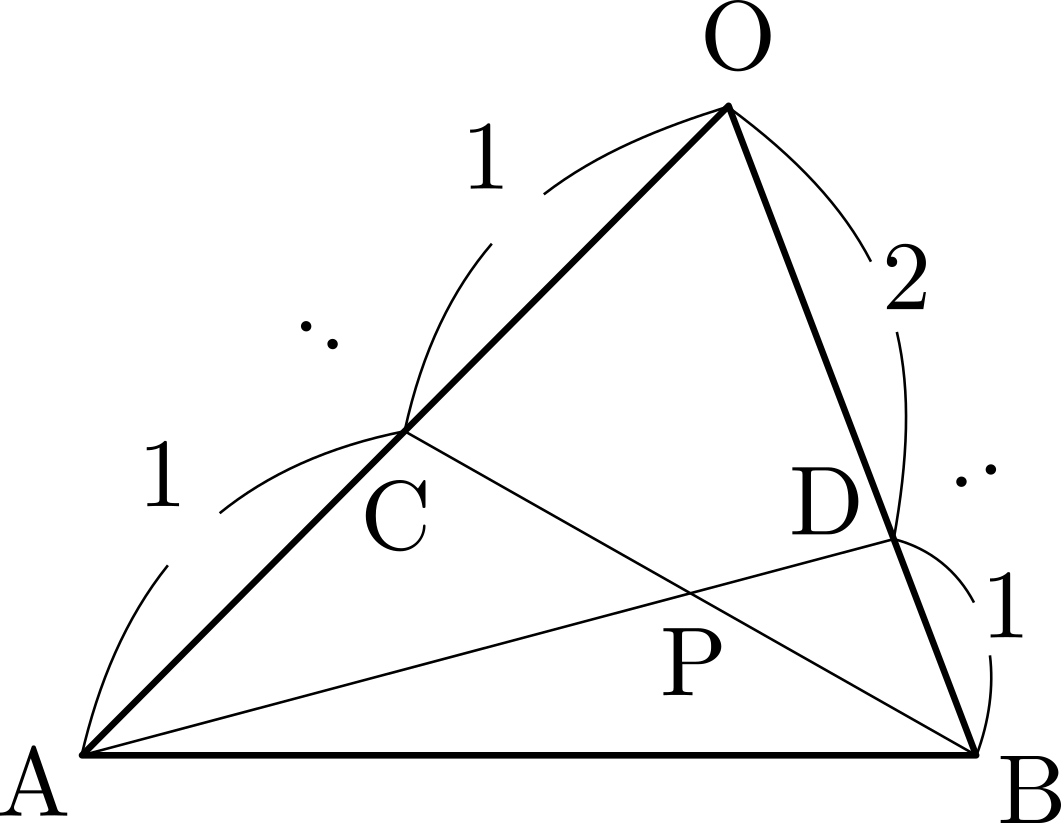
\(\mathrm{OC:CA}=1:1\)であるから,\(\triangle{\mathrm{PBO}}:\triangle{\mathrm{PBA}}=1:1\)
また,\(\mathrm{OD:DB}=2:1\)であるから,\(\triangle{\mathrm{PAO}}:\triangle{\mathrm{PAB}}=2:1\)
よって,\(\triangle{\mathrm{PAO}}:\triangle{\mathrm{PAB}}:\triangle{\mathrm{PBO}}=2:1:1\)
上の公式により,
\begin{align*}
\overrightarrow{\mathrm{OP}}=&\frac{1}{2+1+1}(1\overrightarrow{\mathrm{OA}}+2\overrightarrow{\mathrm{OB}})\\
=&\frac{1}{4}\overrightarrow{\mathrm{OA}}+\frac{1}{2}\overrightarrow{\mathrm{OB}}
\end{align*}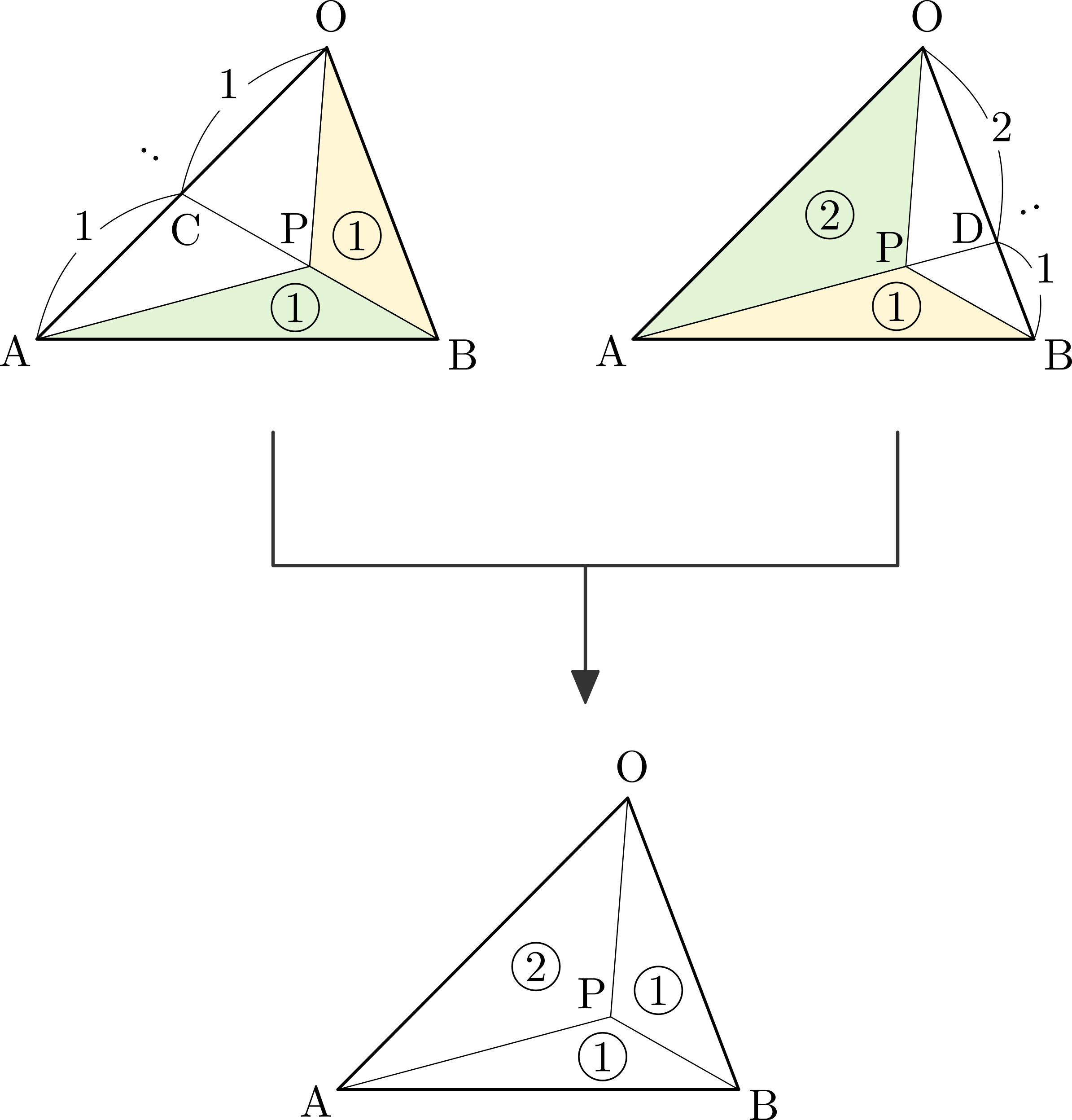
解答終
というように早くて楽…なんですが,しかしこれは教科書に載っていないため,試験で使ってよいかというと微妙なところだと思います。(証明を含めてかけばもちろん問題はないけど,それだと時間がかかり本末転倒)
なので,検算に用いるとよいと思います。

