前記事の証明は
\(n=1\)のとき，\((3+i)^1=3+i\)は虚数．
\(n=2\)のとき，\((3+i)^2=18+26i\)より，実部と虚部を\(10\)で割った余りはそれぞれ\(8,6\)である．\((3+i)^n=\alpha+\beta i,~\alpha\equiv 8 \pmod{10},~\beta\equiv 6 \pmod{10}\)と仮定する．このとき，
\begin{align*}
(3+i)^{n+1}=&(3+i)(3+i)^n\\
=&(3+i)(\alpha+\beta i)\\
=&(3\alpha-\beta)+(\alpha+3\beta)i\\
\end{align*}ここで，
\begin{align*}
&3\alpha-\beta \equiv 3\cdot 8 -6=18\equiv 8\pmod{10}\\
&\alpha+3\beta \equiv 8 + 3\cdot 6=18\equiv 6\pmod{10}\\
\end{align*}
であるから，上の仮定のもとで\[(3+i)^{n+1}=\alpha^{\prime}+\beta^{\prime} i,~\alpha^{\prime}\equiv 8 \pmod{10},~\beta^{\prime}\equiv 6 \pmod{10}\]が成り立つ．したがってすべての\(n\in\{2,3,\cdots\}\)で\[(3+i)^n=\alpha+\beta i,~\alpha\equiv 8 \pmod{10},~\beta\equiv 6 \pmod{10}\]が成り立つ，よって\((3+i)^n\)は虚数となる．以上によりすべての\(n\in\mathbb{N}\)で\((3+i)^n\)は虚数となる．
証明終
となります。この解答の流れを図示すると，以下のようになります：
ここで「解法を覚える」ということはどういうことかを考えてみます。「解法を覚える」というと，上の図で示した解法を「パターン」として機械的に覚えるもの…と解釈する人は少なくないようです。しかし「パターン」として機械的に覚えるだけでは例えばなぜ冒頭でいきなり\(n=1\)と\(n=2\)をあのような形で別々に扱ったのか，なぜ\((3+i)^n=\alpha+\beta i,~\alpha\equiv 8 \pmod{10},~\beta\equiv 6 \pmod{10}\)と仮定しようと思いついたのか，その動機がまったく不明瞭なままです。実際の試験場では当然ながら自分にヒントを与えてくれる人はおらず頼りになるのは自分しかいないわけですから，その解法自体を思いつくためのきっかけ（必然性）こそが重要なはずです。
そこで改めて上の解答に至った経緯を見直してみます。「\(\alpha\equiv 8,\beta \equiv 6\)」と仮定したのは幾度かの試行錯誤の末得られたものでした。そしてそれにより「\(n=2\)のとき別個に調べる」必要が生じました。図示すれば，以下のようになります。
したがって，覚えるべきは流れは以下のようになります。
冒頭の図で示したような直線的な流れではなく，紆余曲折があり，そこから必然性が生まれる，ということです。覚えるのならば，この必然性を含めて覚える。数学における「覚える」とはこのような姿勢でなければなりません。
尚，このような「必然性」は，一般には解答・解説には載っていません。指導してれる人がいない限り，基本自分でそれを読み取らなければならない。だから数学の解答を読む際は「なぜ？」と問いかけながら，あたかも本と対話するように読むことが重要です。もし本の解答解説が必然性が感じられない，天下り的なものであれば，自分の手で発見的な解答に作り直す，くらいの気持ちをもつべきだと思います。
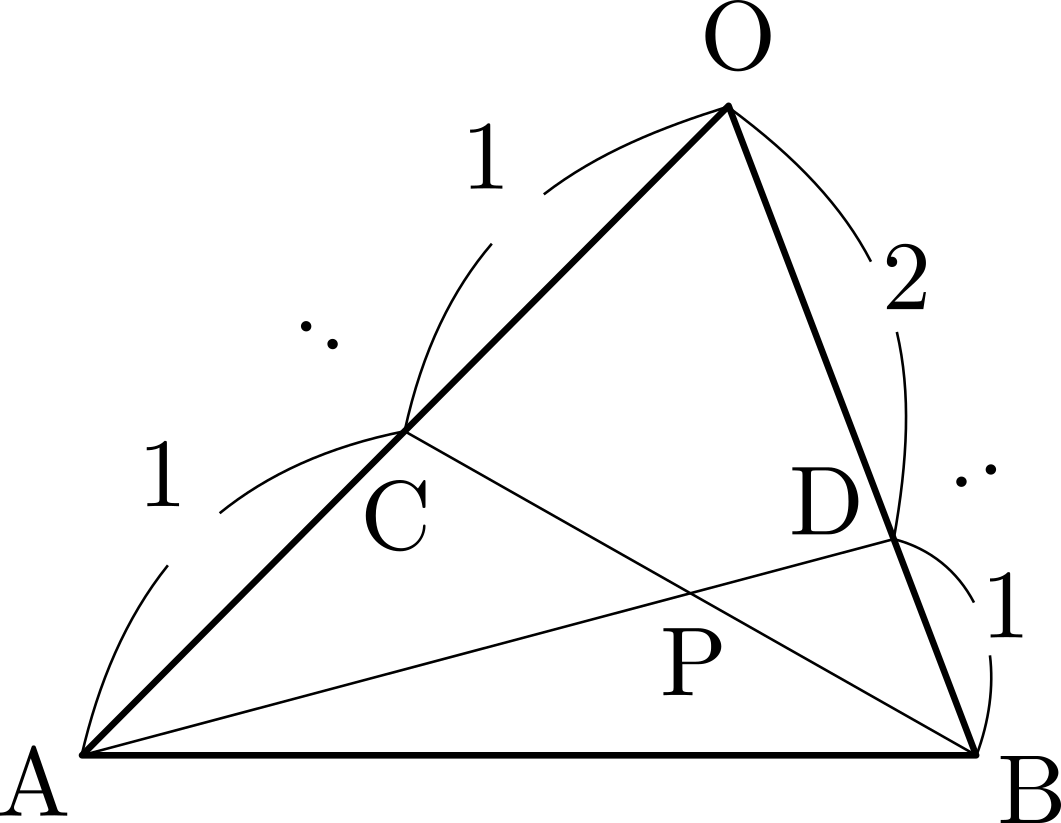
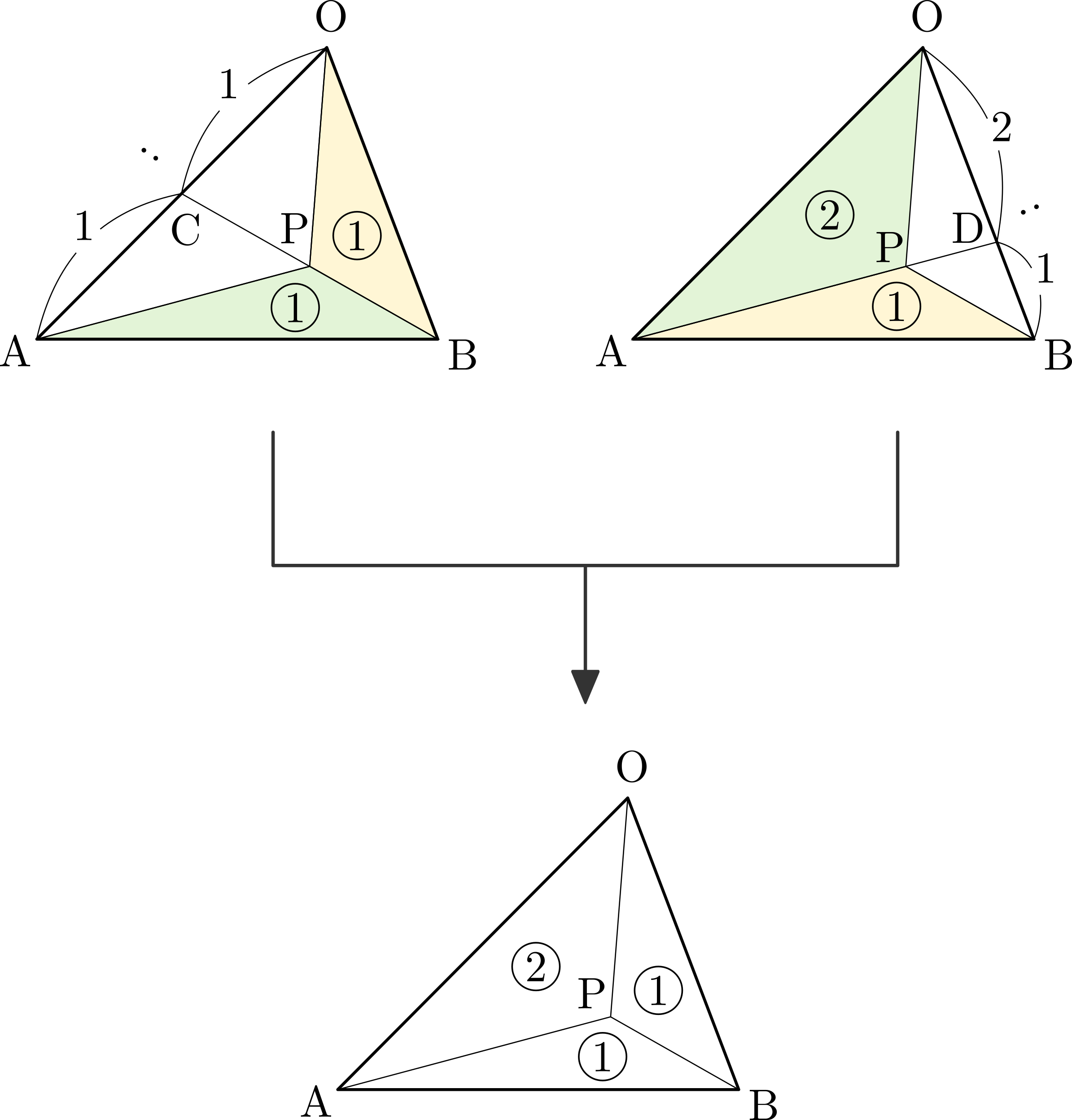
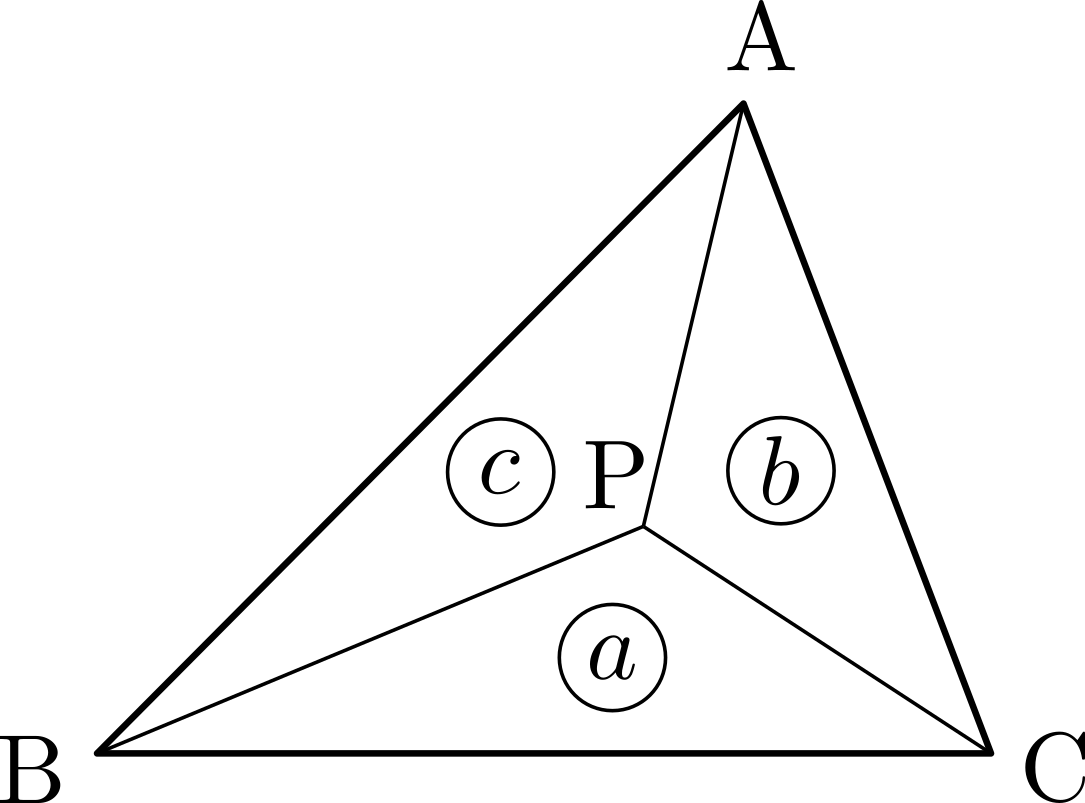\(\triangle{\mathrm{ABC}}\)において，\(\triangle{\mathrm{PBC}}:\triangle{\mathrm{PCA}}:\triangle{\mathrm{PAB}}=a:b:c~\)のとき，\[\overrightarrow{\mathrm{AP}}=\frac{1}{a+b+c}(b\overrightarrow{\mathrm{AB}}+c\overrightarrow{\mathrm{AC}})\]
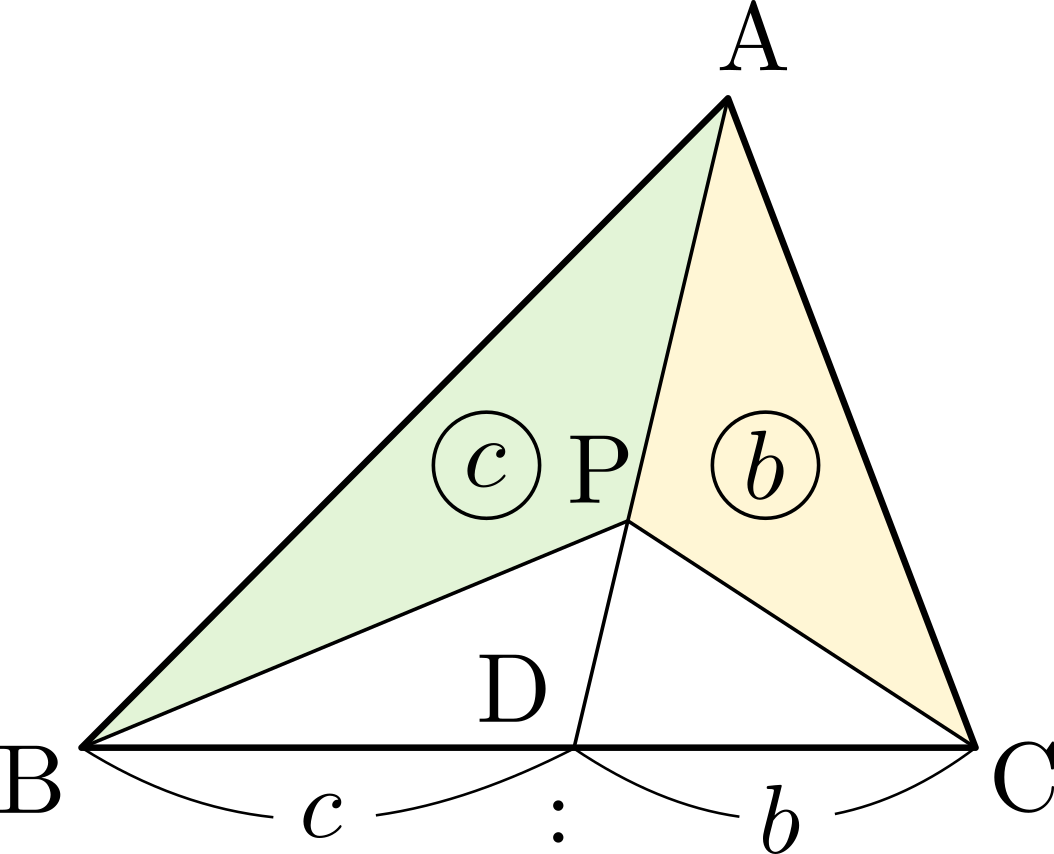直線\(\mathrm{AP}\)と辺\(\mathrm{BC}\)との交点を\(\mathrm{D}\)とおくと，\(\triangle{\mathrm{PCA}}:\triangle{\mathrm{PAB}}=b:c\)より\(\mathrm{BD}:\mathrm{DC}=c:b\)であるから，内分の公式により\[\overrightarrow{\mathrm{AD}}=\frac{b\overrightarrow{\mathrm{AB}}+c\overrightarrow{\mathrm{AC}}}{c+b}\]
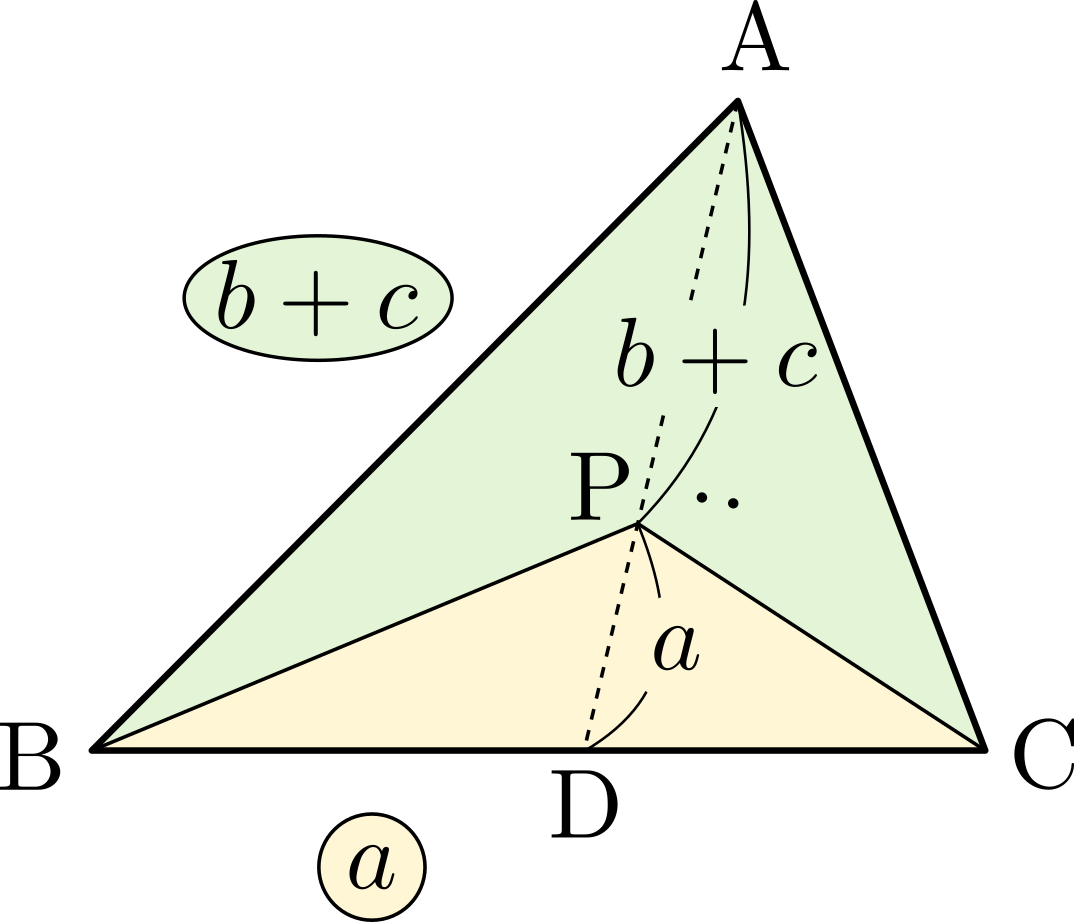また，凹四角形\(\mathrm{ABPC}\)と\(\triangle{\mathrm{PBC}}\)の面積比が\(b+c:a\)であることから\(\mathrm{AP}:\mathrm{PD}=b+c:a\)だから\[\overrightarrow{\mathrm{AP}}=\frac{b+c}{a+b+c}\overrightarrow{\mathrm{AD}}\]
