(田島一郎解析入門P16問16)
(証明)
与えられた仮定は\(\displaystyle \lim_{x \Rightarrow a}g(x)=\beta\)すなわち
\[\forall \epsilon>0 \exists \delta>0 \big[0<|x-a|<\delta \Longrightarrow |g(x)-\beta|<\epsilon \big]\tag{\(\ast\)}\] である.問15より,この仮定から \[\beta >0 \text{のとき,}0 < \frac{|\beta|}{2} < g(x) < \frac{3}{2}|\beta|\tag{1}\]
\[\beta <0 \text{のとき,}-\frac{3}{2}|\beta| < g(x) < -\frac{|\beta|}{2} < 0\tag{2}\]
という結論を得たのだった.\((1),(2)\)から,
\[
\begin{align*}
(1)\Longrightarrow~& \frac{|\beta|}{2} < |g(x)| < \frac{3}{2}|\beta|\\
(2)\Longrightarrow~&-\frac{3}{2}|\beta| < g(x) < -\frac{|\beta|}{2}\\
\Longrightarrow~&-\frac{3}{2}|\beta| < -|g(x)| < -\frac{|\beta|}{2}\\
\Longrightarrow~&\frac{|\beta|}{2} < |g(x)| < \frac{3}{2}|\beta|\\
\end{align*}
\]
となり結局\(\beta\)の正負に関わらず\[\frac{|\beta|}{2} < |g(x)| < \frac{3}{2}|\beta|\tag{\(\ast\ast\)}\]が得られることになる.
さて,今示したいのは \[\displaystyle \lim_{x \rightarrow a} \frac{1}{g(x)}=\frac{1}{\beta}\] すなわち \[\forall \epsilon>0 \exists \delta’>0 \left[0<|x-a|<\delta’ \Longrightarrow \left|\frac{1}{g(x)}-\frac{1}{\beta}\right|<\epsilon \right]\]
であった.ここで任意の\(\epsilon\)に対応する\(\delta’\)として\(\delta\)ととることにする.すると,この\(\delta\)のもとで
\[0<|x-a|<\delta \Longrightarrow \left|\frac{1}{g(x)}-\frac{1}{\beta}\right|<\epsilon\]
が成り立つかどうか,すなわち
\[
\begin{align*}
&\left|\frac{1}{g(x)}-\frac{1}{\beta}\right|=\left|\frac{\beta-g(x)}{\beta g(x)}\right|=\frac{|g(x)-\beta|}{|\beta| |g(x)|}
\end{align*}
\]
より
\[0<|x-a|<\delta \Longrightarrow \frac{|g(x)-\beta|}{|\beta| |g(x)|}<\epsilon\]
が成り立つかどうかが問題となるが,これは仮定\((\ast)\),\((\ast\ast)\)より
\[\frac{|g(x)-\beta|}{|\beta| |g(x)|}<\frac{\epsilon}{|\beta|\frac{|\beta|}{2}}=\frac{2\epsilon}{\beta^2}\]
となり確かに成り立つ.(証明終)


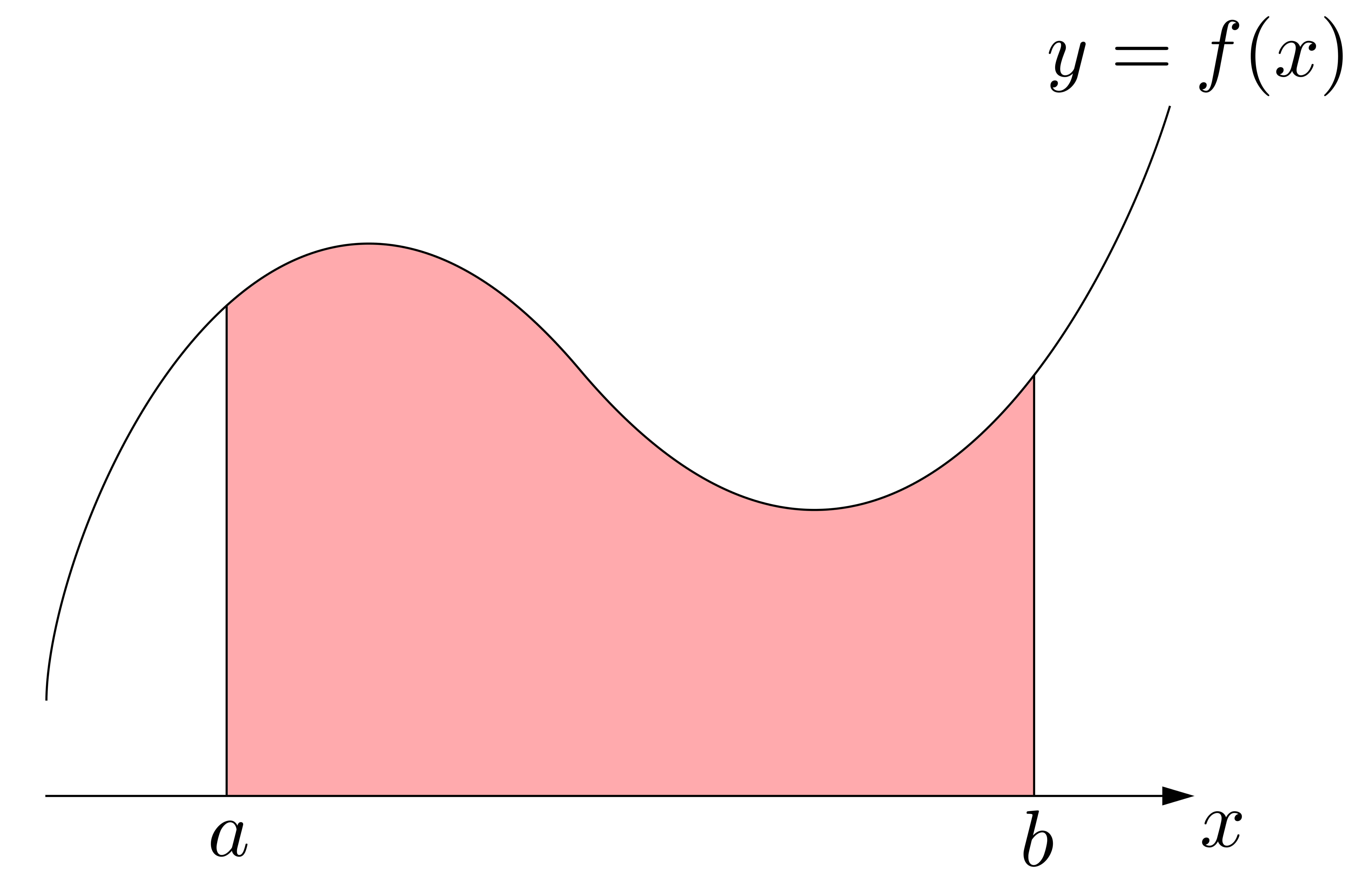
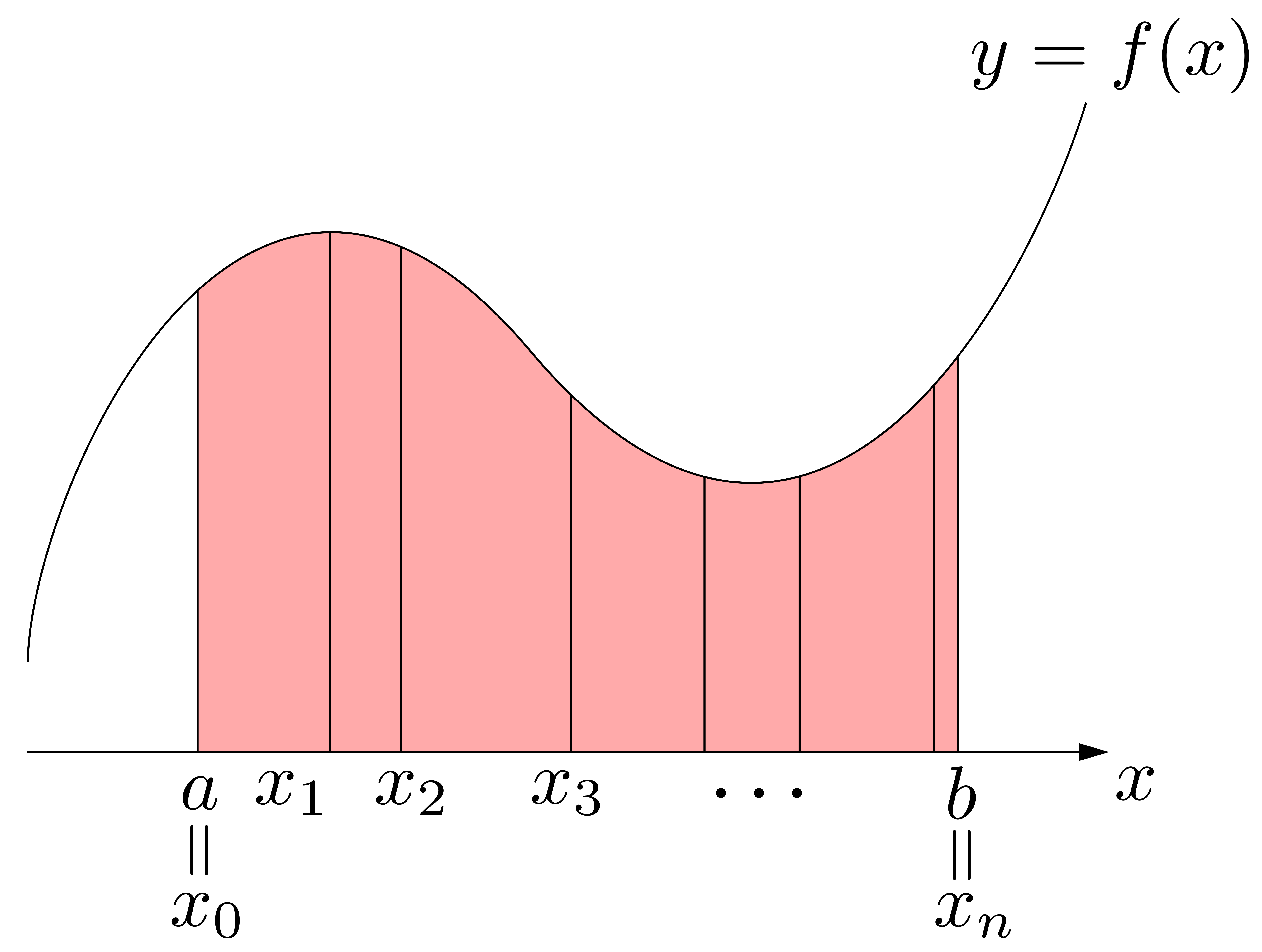
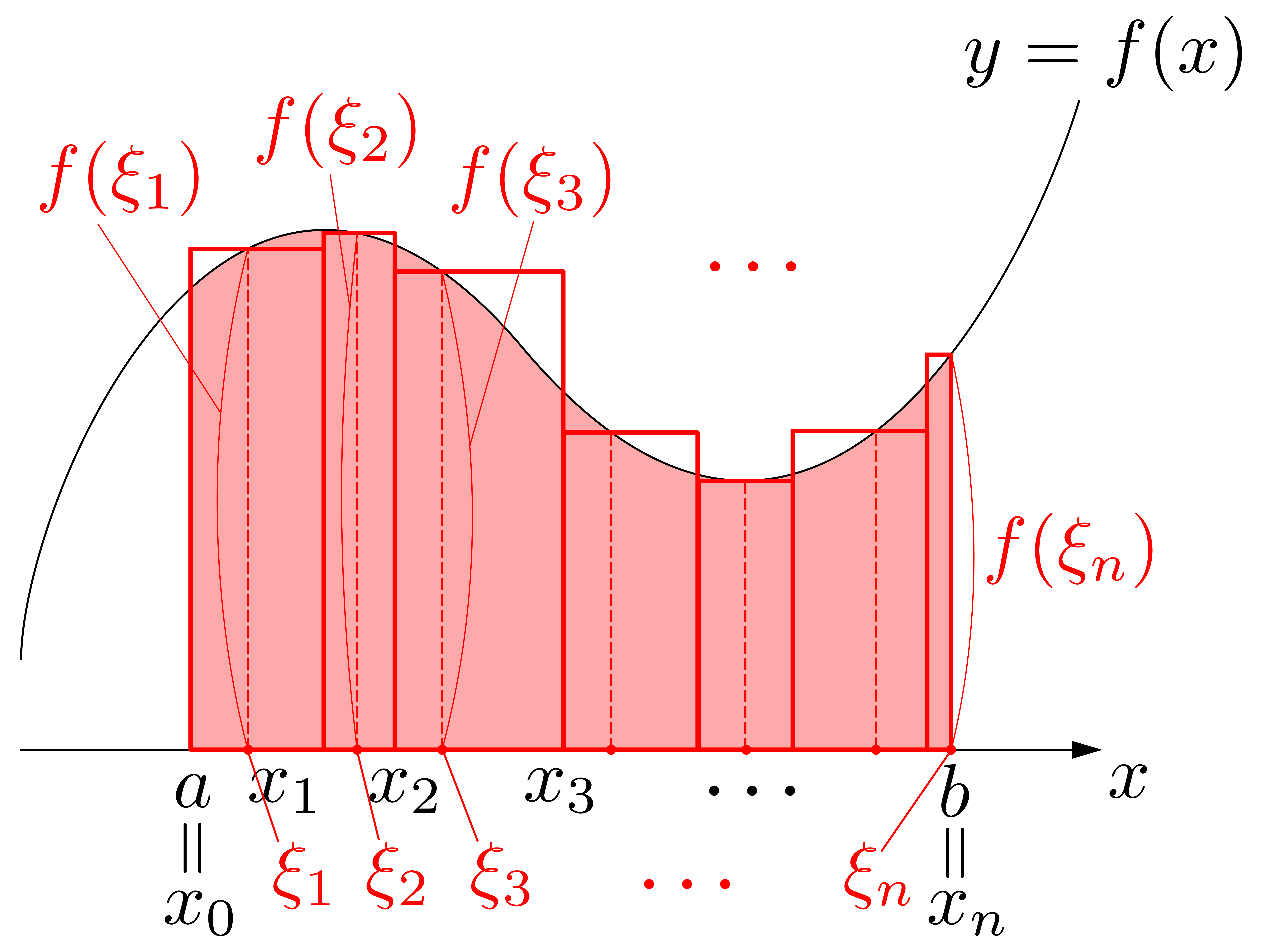

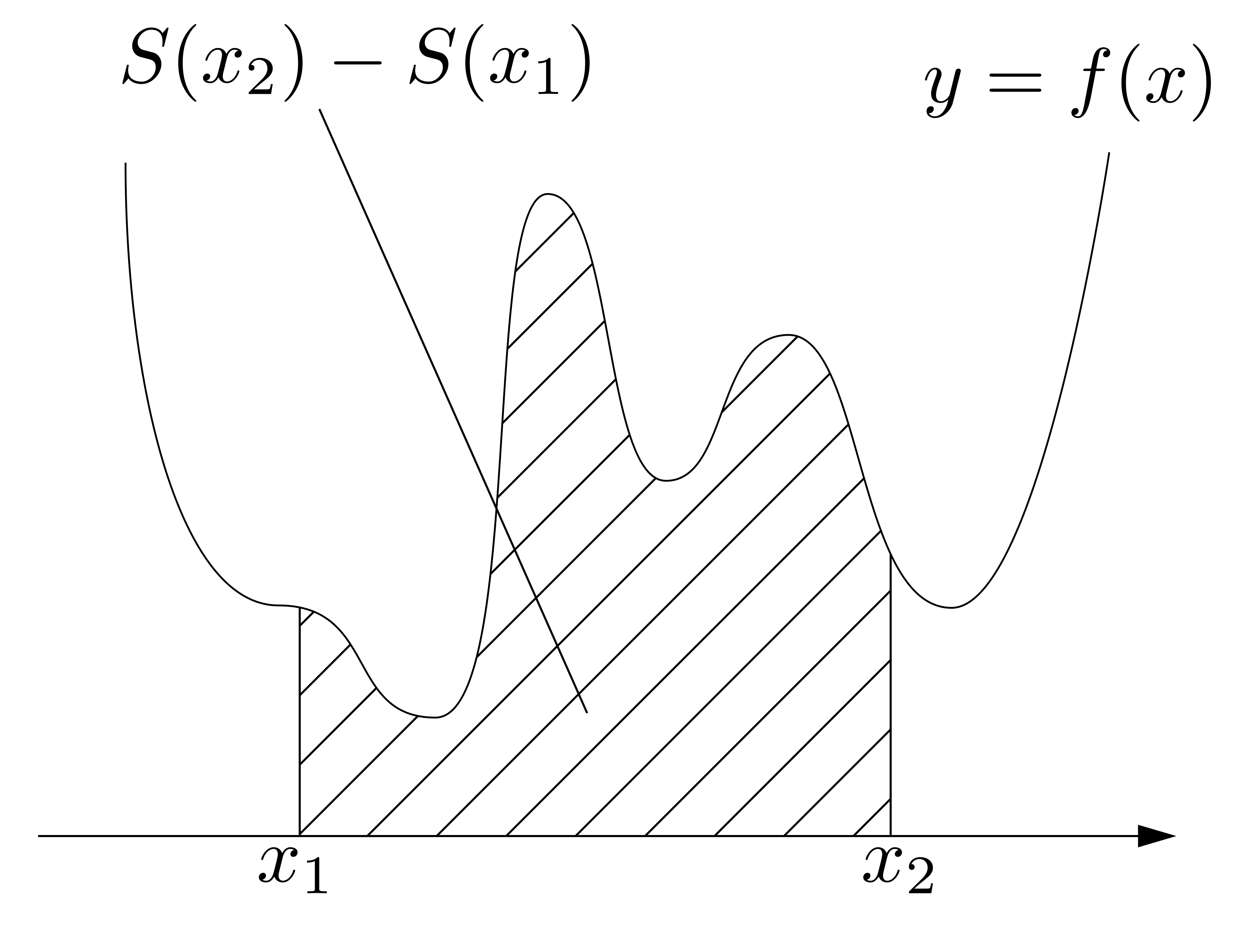
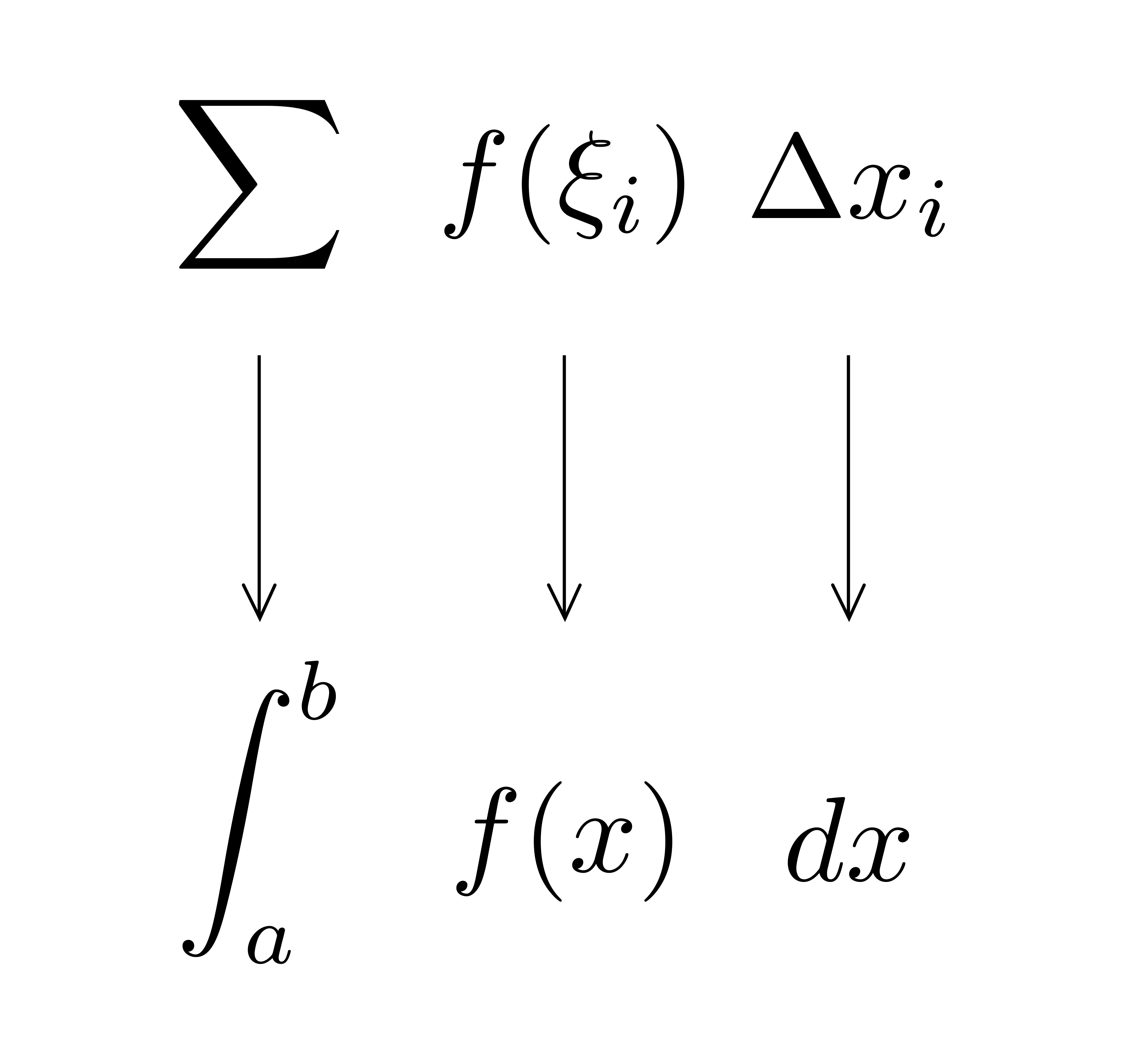 以上を見ると,\(\displaystyle \int^b_a f(x)dx\)の\(\displaystyle \int\)や\(dx\)の「イメージ」が見えてきます.右図に示すように,\(\displaystyle \sum\)が\(\displaystyle \int\)に,\(\Delta x_i\)が\(dx\)と対応しているわけです.
以上を見ると,\(\displaystyle \int^b_a f(x)dx\)の\(\displaystyle \int\)や\(dx\)の「イメージ」が見えてきます.右図に示すように,\(\displaystyle \sum\)が\(\displaystyle \int\)に,\(\Delta x_i\)が\(dx\)と対応しているわけです.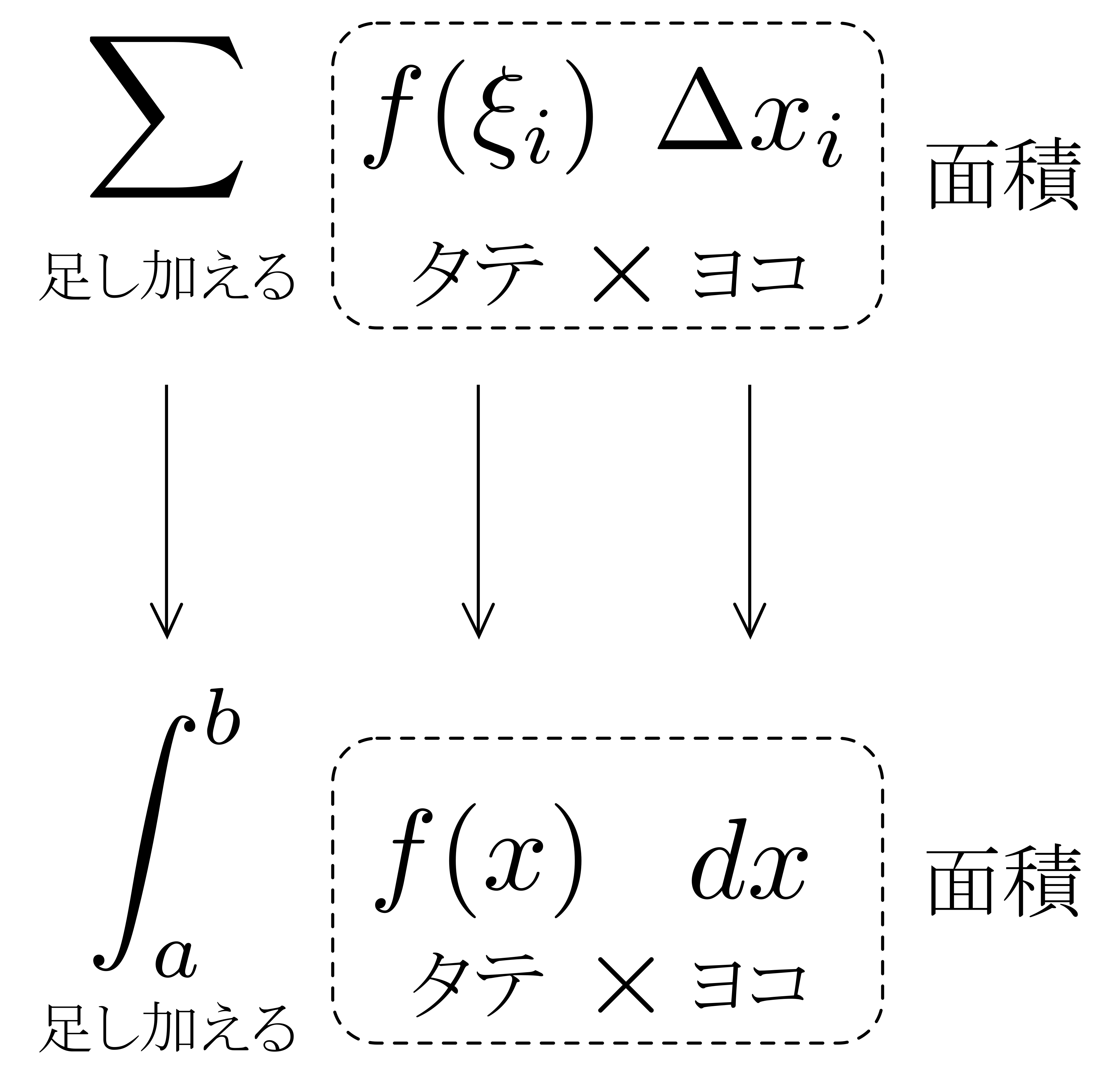 以上を踏まえて\(\displaystyle \int^b_a f(x)dx\)を眺めると,これは「微小面積\(f(x)\times dx\)を\(\displaystyle \int\)したもの(連続的に足し加えたもの)」と読み取れることが分かります!
以上を踏まえて\(\displaystyle \int^b_a f(x)dx\)を眺めると,これは「微小面積\(f(x)\times dx\)を\(\displaystyle \int\)したもの(連続的に足し加えたもの)」と読み取れることが分かります!