命題や条件は,分配することができます.すなわち,
\[(p\lor q)\land r \Longleftrightarrow (p \land r)\lor (q \land r)\]や\[(p\land q)\lor r \Longleftrightarrow (p \lor r)\land (q \lor r)\]などが成り立ちます.
証明
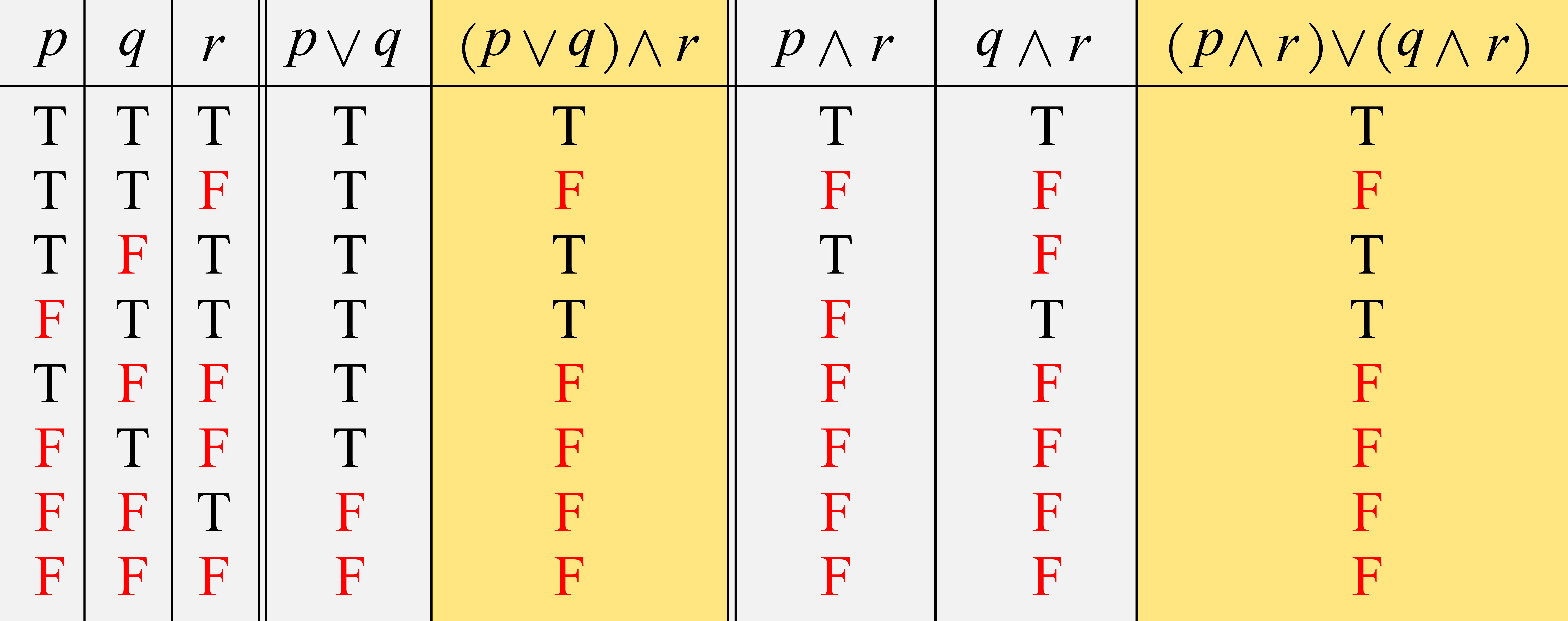
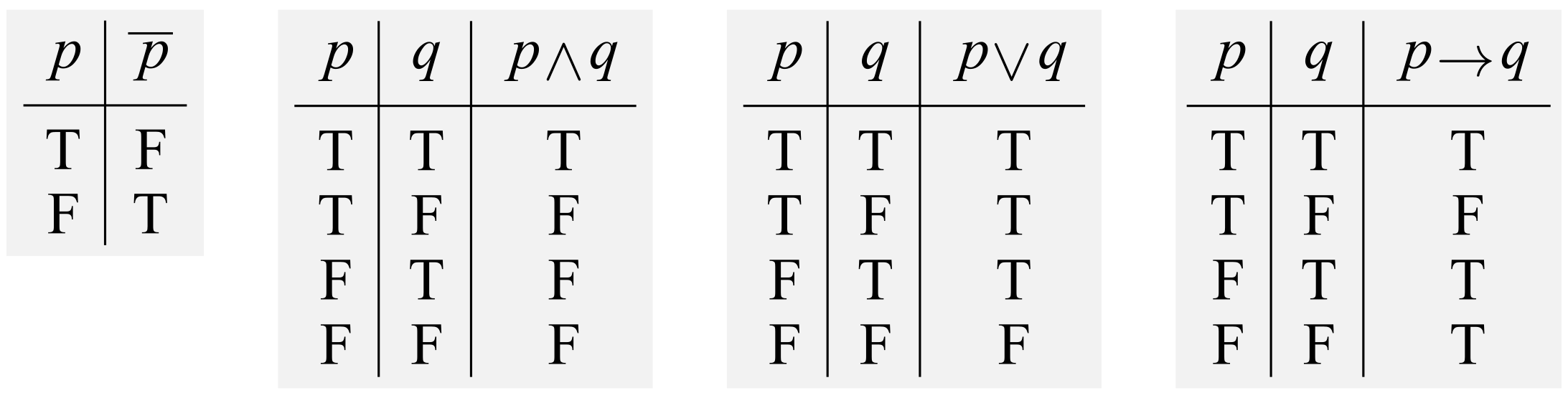
真理表で確認します.
まず,\(p,~q,~r\)の真偽は\(2^3=8\)通りあることに注意して,

と書けます.見やすさのためにFを赤色にしました.
次に\(p\lor q\)を書き,その列を埋めましょう.\(p\)の列と\(q\)の列に着目して,\(\lor\)の定義に従うと,

と書けます.次に\((p\lor q)\land r\)を書き,その列を埋めます.\(p\lor q\)と\(r\)の列に着目して,\(\land\)の定義に従うと,

と書けます.
今度は\( (p \land r)\lor (q \land r)\)について調べます.そのためにはまず\((p \land r)\)と\((q \land r)\)を調べなくてはなりません.なのでまず,\(p\lor r\)と\(q \land r\)を書き,それぞれの列を埋めましょう.\(p\)の列と\(r\)の列,そして\(q\)の列と\(r\)の列に着目して\(\land\)の定義に従うと,

と書けます.さて,準備ができたので\( (p \land r)\lor (q \land r)\)を書いてその列を埋めていきましょう.先ほど書いた\( (p \land r)\)と\((q \land r)\)の列に着目して\(\lor\)の定義に従うと,

と書けます.
さて,ここで\((p\lor q)\land r\)と\((p \land r)\lor (q \land r)\)の列に着目しましょう.すると,真理値が同じですね.同値\(\leftrightarrow\)の定義より,\((p\lor q)\land r\)と\((p \land r)\lor (q \land r)\)が同値であることが分かります.
これで,\((p\lor q)\land r \Longleftrightarrow (p \land r)\lor (q \land r)\)であることが証明できました.同様にして,\((p\land q)\lor r \Longleftrightarrow (p \lor r)\land (q \lor r)\)が証明できます.






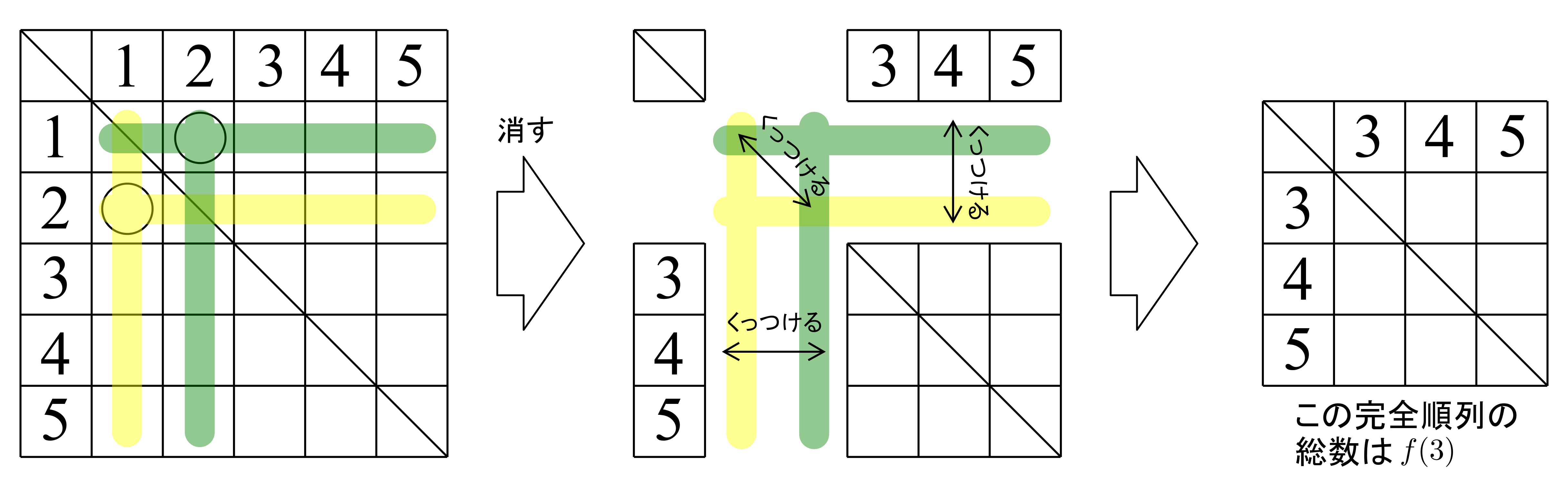
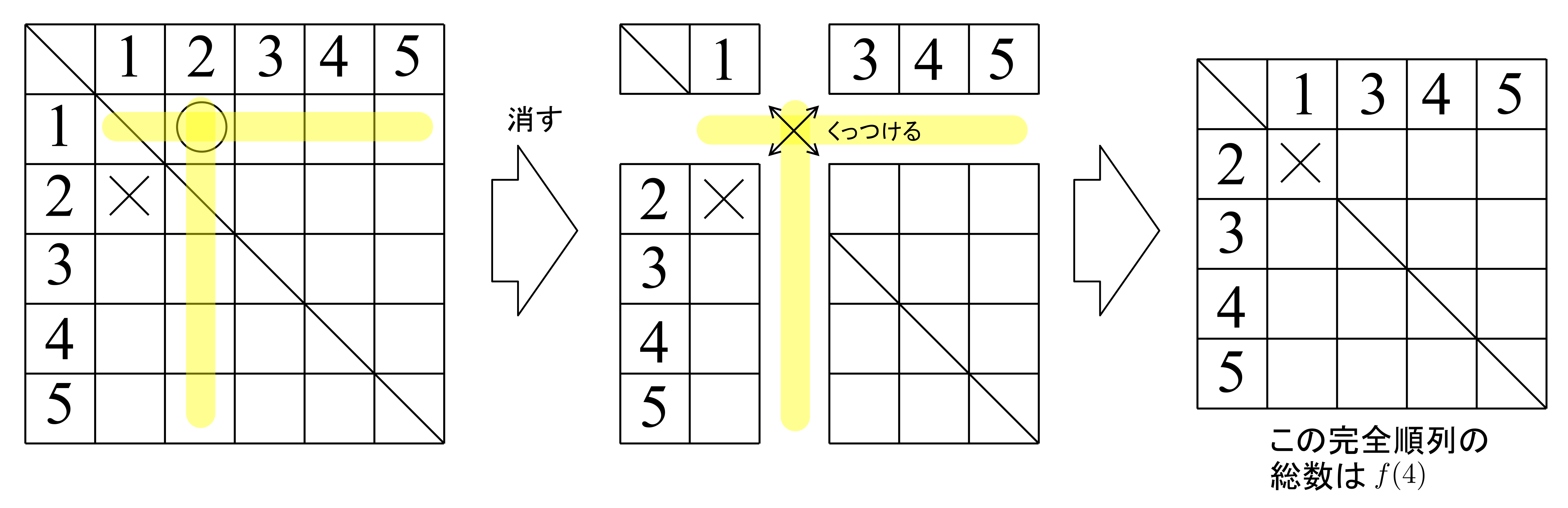
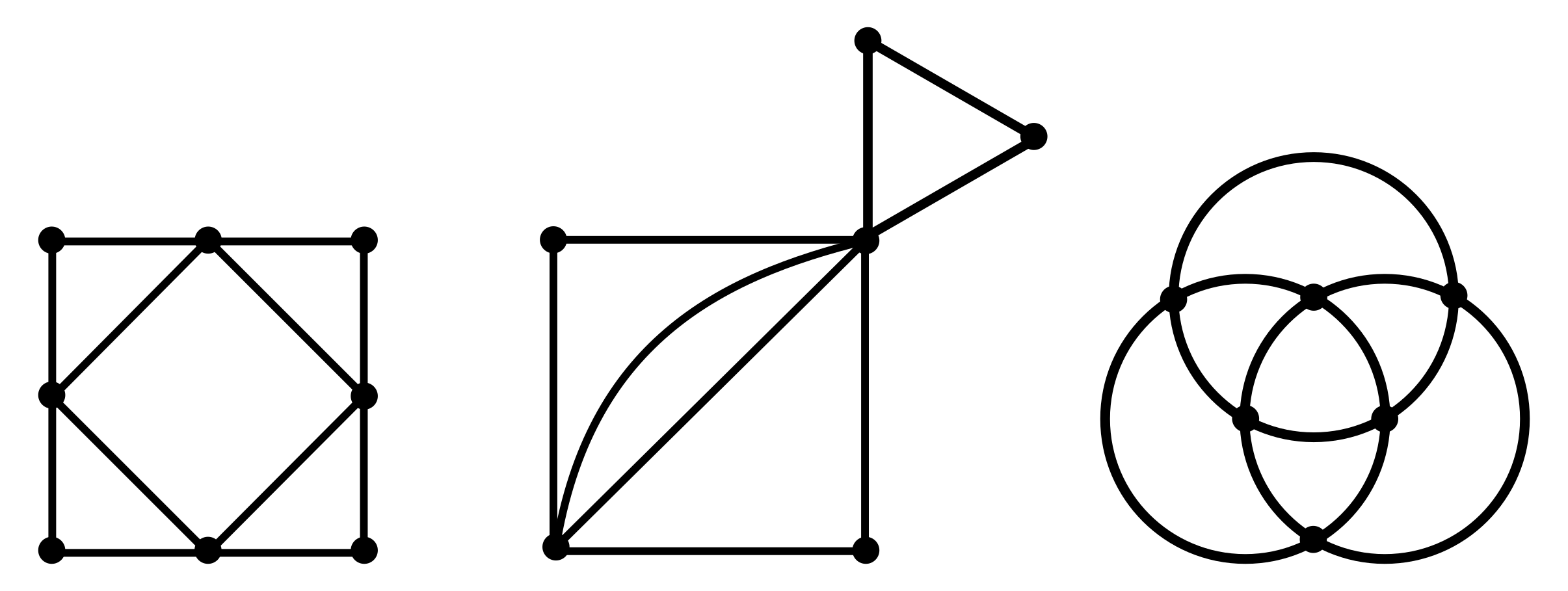
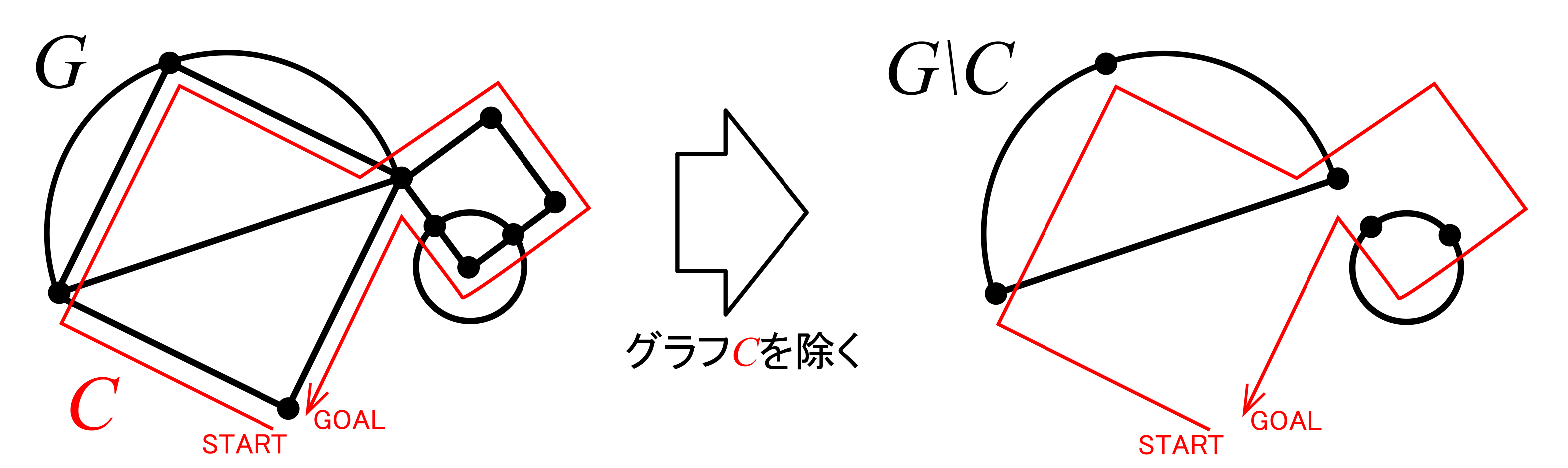
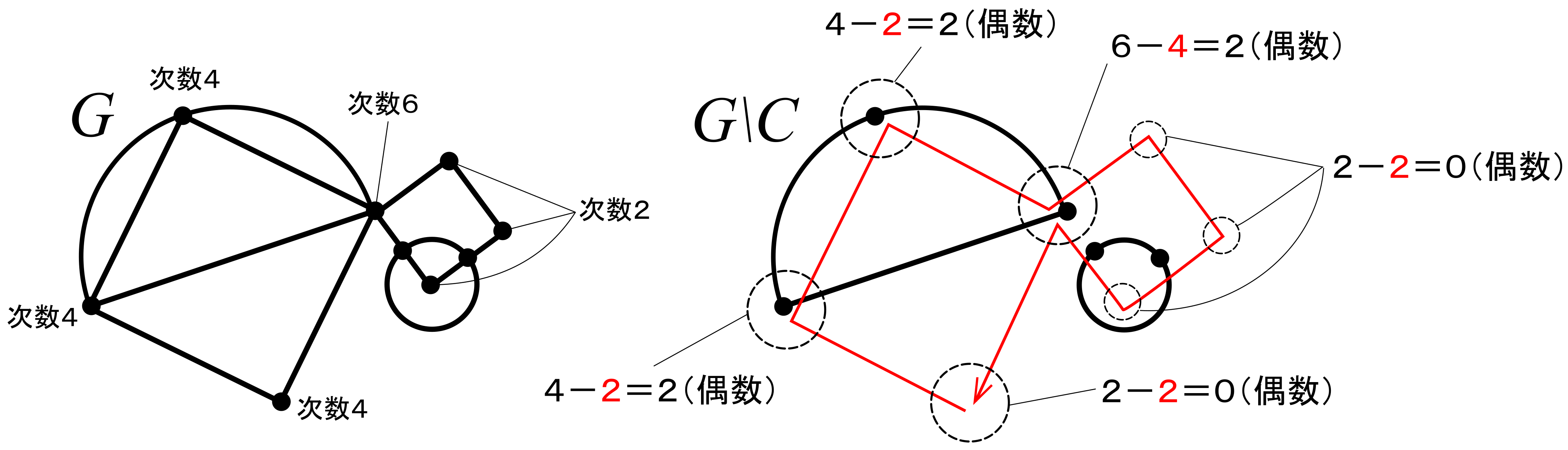
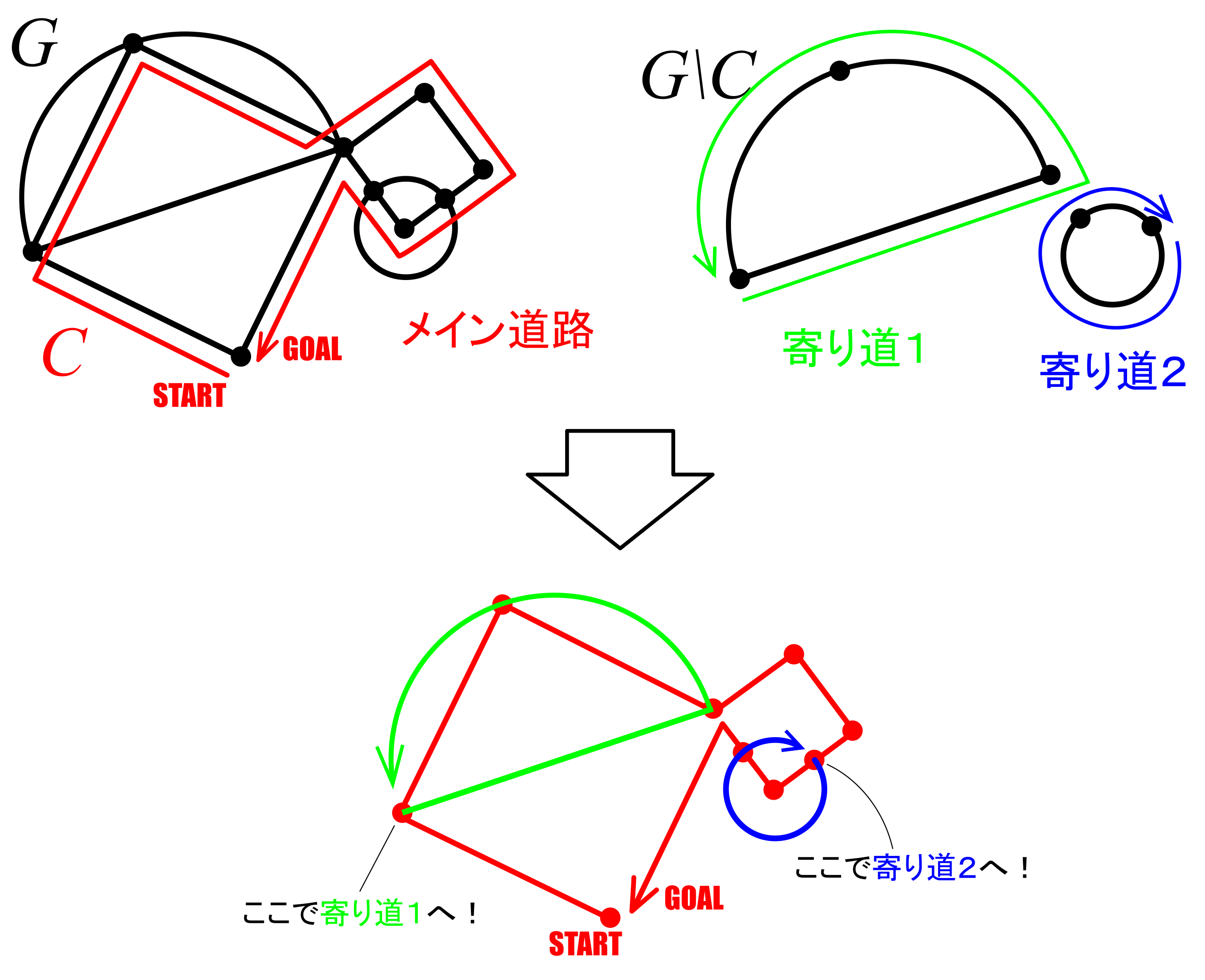
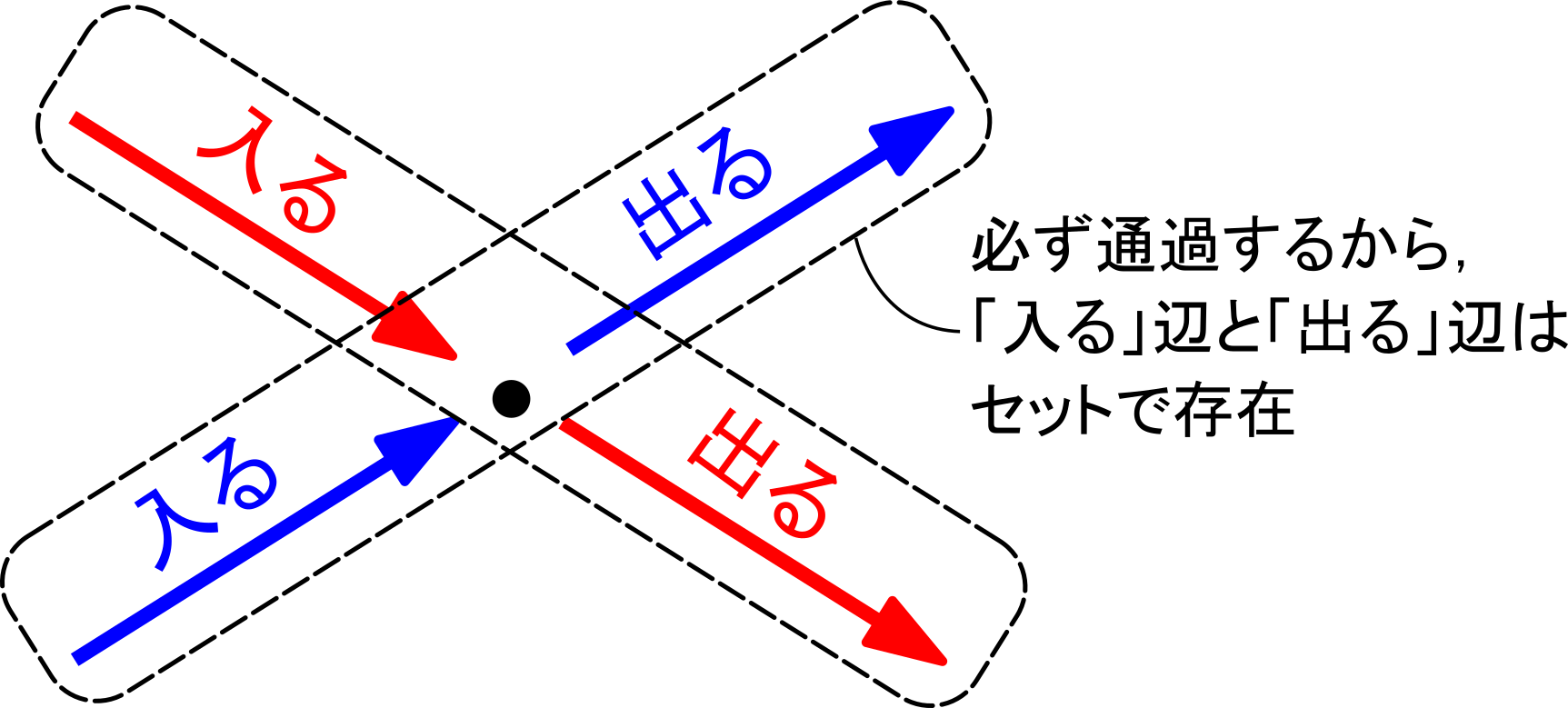 グラフがオイラーグラフであるとする.オイラーグラフとはいわば「一筆書きして出発点に戻ってこられる」ようなグラフであるから,各頂点において,その頂点で袋小路になることなく通過できることになる.これはその頂点に「入る」辺があれば必ず「出ていく」辺もセットで存在することを意味する(2本がセットとなる).したがって各頂点における次数は2の倍数となる.ゆえに,すべての頂点は偶点であるといえる.
グラフがオイラーグラフであるとする.オイラーグラフとはいわば「一筆書きして出発点に戻ってこられる」ようなグラフであるから,各頂点において,その頂点で袋小路になることなく通過できることになる.これはその頂点に「入る」辺があれば必ず「出ていく」辺もセットで存在することを意味する(2本がセットとなる).したがって各頂点における次数は2の倍数となる.ゆえに,すべての頂点は偶点であるといえる.