カテゴリー: 数学Ⅲ

（数学Ⅲ）

不等式の証明のアプローチのひとつとして微分法の利用があります。

証明

まず\(b\geq 0\)を固定して，\[ab \leq \frac{a^p}{p}+\frac{b^q}{q} \Longleftrightarrow~ \frac{1}{p}a^p-ba+\frac{b^q}{q}\geq 0\]と変形し，左辺を\(a\)の関数と見なす．この関数を\(f(a)\)とおく：\[f(a)=\frac{1}{p}a^p-ba+\frac{b^q}{q} \quad (a\geq 0)\]\(f^{\prime}(a)\)を調べると，\[f^{\prime}(a)=a^{p-1}-b\]\(a^{p-1}\)の概形が分からないので，もう一度微分することで\(f^{\prime}(a)\)がどんな概形かを調べる（※）．すると\[f^{\prime\prime}(a)=(p-1)a^{p-2}\geq 0\]したがって\(f^{\prime}(a)\)は増加関数であることが分かる．\(a\geq 0\)であったことに注意して\(a=0\)のときの\(f^{\prime}(a)\)の値を調べると\[f^{\prime}(0)=-b\]

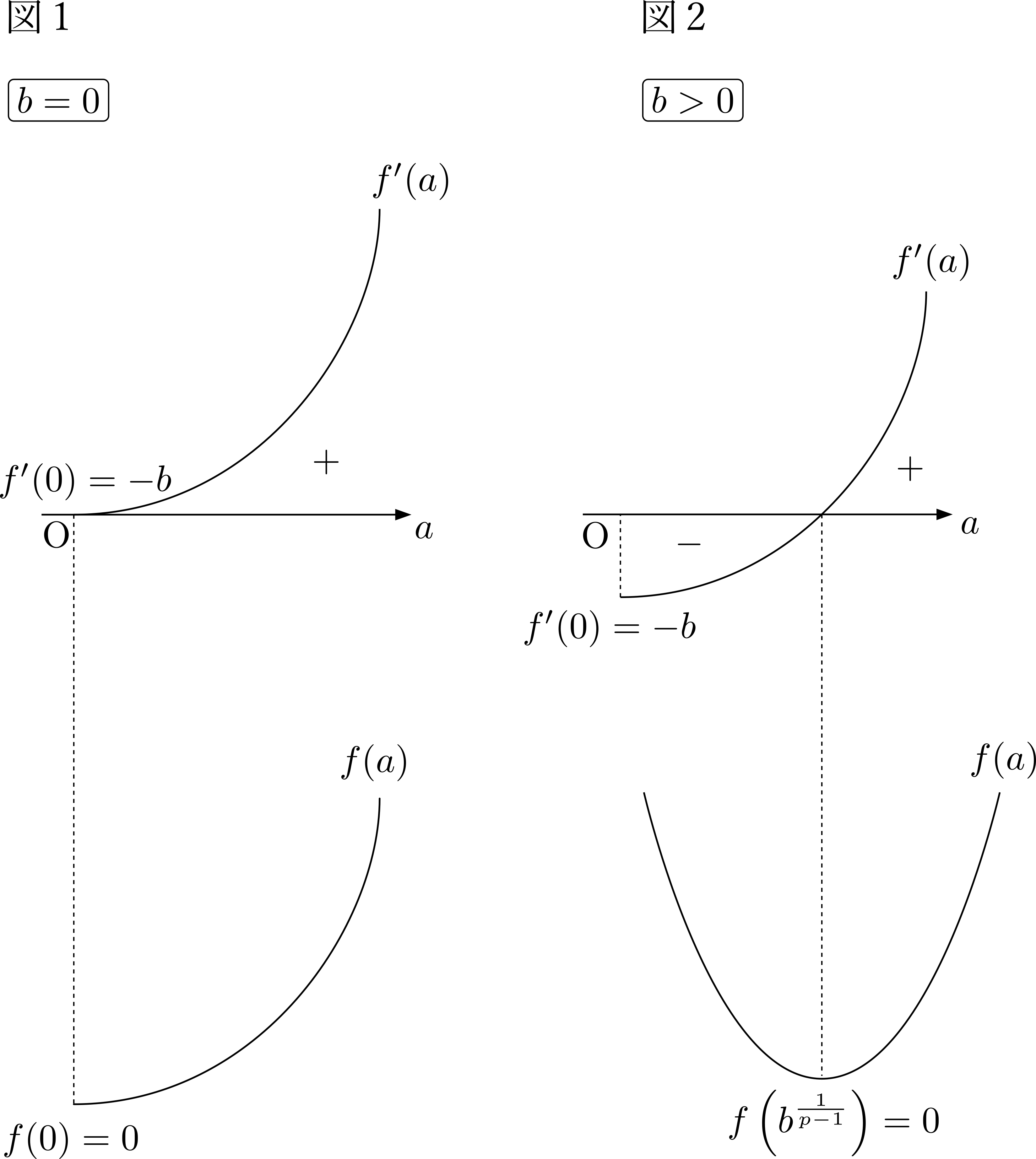
\(b=0\)のときは，\(f^{\prime}(0)=0\)であるから\(f^{\prime}(a)\geq 0\)となる．\(f(0)\)を調べると\(f(0)=\frac{b^q}{q}= 0\)であるから\(f(a)\geq 0\)．（図１）

\(b>0\)のときすなわち\(-b<0\)のときは，\(f^{\prime}(a)=a^{p-1}-b=0 \Longleftrightarrow a=b^{\frac{1}{p-1}}\)で最小値をとる．

そこで\(f\left(b^{\frac{1}{p-1}}\right)\)を調べると
\begin{align*}
f\left(b^{\frac{1}{p-1}}\right)=&\frac{1}{p}\left(b^{\frac{1}{p-1}}\right)^p-b\cdot b^{\frac{1}{p-1}}+\frac{b^q}{q}\\
=&\frac{1}{p}b^{\frac{p}{p-1}}-b^{\frac{p}{p-1}}+\frac{b^q}{q}
\end{align*}
ここで，\(\frac{1}{p}+\frac{1}{q}=1\Leftrightarrow q=\frac{p}{p-1}\)であるから，\[f\left(b^{\frac{1}{p-1}}\right)=\frac{1}{p}b^q-b^q+\frac{1}{q}b^q=\left(\frac{1}{p}+\frac{1}{q}-1\right)b^q=0\]したがって\(f(a)\geq 0\)．（図２）

以上により\[ab \leq \frac{a^p}{p}+\frac{b^q}{q}\]が示された．

証明終

※は概形が図示できず，かつ「差」とみても把握できないタイプなのでもう一回微分して\(f^{\prime\prime}(a)\)を調べました。この記事の「増減表のかきかた」の②”にあたる状況です。

上の放物線と直線で囲まれる部分の面積\(S\)は，いずれの場合も\[S = \frac{|a|(\beta-\alpha)^3}{6}\]で表される．

証明

\(a>0\)の場合と\(a<0\)の場合とで場合を分けて考える．

（\(a>0\)の場合）

被積分関数\(g(x)-f(x)\)がどんな関数になるかを考える．これは，

• • • \(2\)次式で，
    • 次数が一番大きい項の係数は\(-a\)で，
    • 交点が\(\alpha,\beta\)すなわち\(g(x)-f(x)=0\)を解いて得られる\(2\)つの解が\(\alpha,\beta\)である

ことに着目すると，\[f(x)-g(x)=-a(x-\alpha)(x-\beta)\]とかける．したがって求める部分の面積は
\begin{align*}
&\displaystyle \int_{\alpha}^{\beta} -a(x-\alpha)(x-\beta) dx \\
=~&\displaystyle a\int_{\alpha}^{\beta} -(x-\alpha)(x-\beta) dx\\
=~&\frac{a(\beta-\alpha)^3}{6}\tag{1}\\
=~&\frac{|a|(\beta-\alpha)^3}{6}
\end{align*}

（\(a<0\)の場合）

被積分関数は\(f(x)-g(x)\)であるから，上と同様に考え，\[f(x)-g(x) = a(x-\alpha)(x-\beta)\]したがって求める部分の面積は
\begin{align*}
&\displaystyle \int_{\alpha}^{\beta} a(x-\alpha)(x-\beta) dx \\
=~&\displaystyle -a\int_{\alpha}^{\beta} -(x-\alpha)(x-\beta) dx\\
=~&\frac{-a(\beta-\alpha)^3}{6}\tag{1}\\
=~&\frac{|a|(\beta-\alpha)^3}{6}
\end{align*}
以上により，いずれの場合も面積\(S\)は\[\frac{|a|(\beta-\alpha)^3}{6}\]で表されることになる．

証明終

大事なポイントは被積分関数\(g(x)-f(x),~f(x)-g(x)\)を書くところです。これを実際に書き出して項を整理して因数分解を考え…などと愚直に計算するのは間違いではありませんがあまりよい手とは言えません。上で見たように，\(g(x)-f(x),~f(x)-g(x)\)を特徴付ける（３つの）要素さえ分かってしまえば即答できるわけですから。また，\((1)\)は定積分の有名公式によります。あの公式は具体的にはこんなシチュエーションで役に立つ，ということです。

結局，交点\(\alpha,\beta\)と係数\(a\)という情報だけで面積が求まってしまうということになります．

模試以上の問題ならばこの公式は（そのレベルの問題だとこれは単なる‘途中計算’に過ぎませんから）証明抜きで使っても問題ないと思われます．しかし学校のテストなどは立式～定積分の計算を問う意図もあるかと思うのでもしかしたら嫌がられるかもしれません．とはいえ，学校のテスト（＝教科書の例題・練習題）だとぐちゃぐちゃ計算させようとする問題も多く，そんなのに付き合わせられるのもうざったらしいので，この証明を解答欄の脇にでもササっと記述して以降の問題を公式で済ませてしまうというのもひとつの手だと思います（証明する必要があるかどうかは，作問する先生に事前に確認しておくとよいでしょう）．

他にも覚えておくと便利な公式があります。随時更新していきます．

この曲線を減衰曲線といいます。入試でよく見られるのはこれに絶対値をとったもの，すなわち\[|y|=|e^{-x}\sin x|=e^{-x}|\sin x|\]です．これを\(f(x)\)とおき，その性質について見てみます．

\(f(x):=e^{-x}|\sin x|\)とする．\(f(x+\pi)\)について調べる．
\begin{align*}
f(x+\pi)&=e^{-(x+\pi)}|\sin (x+\pi)|\\
&=e^{-\pi}e^{-x}|\sin x|\\
&=e^{-\pi}f(x)
\end{align*}
これは翻訳すればいわば「現在地点より\(\pi\)だけ先の関数の値は，現在の関数の値を\(e^{-\pi}\)倍したもの」ということです．

これを減衰曲線の性質としてまとめておきます．

このことから，\(y=f(x)~((k-1)\pi \leq x \leq k\pi,k\in \mathbb{N})\)と\(x\)軸で囲まれる部分の面積を\(S(k)\)とおくことにすれば，となりの山に対して縦に\(e^{-\pi}\)だけ縮むわけですから，

が言えることが分かります．

これは，山の面積の間には等比数列の関係があることを意味します．※直観的に明らかですが，念のため計算して確かめておくと，
\begin{align*}
S(k+1)&=\displaystyle \int_{k\pi}^{(k+1)\pi}f(x)dx=\displaystyle \int_{k\pi}^{(k+1)\pi} e^{-x}|\sin x|dx\\
&=\displaystyle \int_{(k-1)\pi}^{k\pi} e^{-(x+\pi)}|\sin(x+\pi)| dx\\
&=\displaystyle e^{-\pi}\int_{(k-1)\pi}^{k\pi} e^{-x}|\sin x| dx\\
&=\displaystyle e^{-\pi}\int_{(k-1)\pi}^{k\pi} f(x) dx\\
&=\displaystyle e^{-\pi}S(k)\\
\end{align*}となり確かに成り立ちます．

さて，以上の準備のもとに次の問題を考えてみましょう．

【解答】
\(\displaystyle \int_0^{n\pi}e^{-x}|\sin x| dx\)は下図の曲線と\(x\)軸で囲まれる部分の面積である．

\(f(x)=e^{-x}|\sin x|\)そして\(~y=f(x)~((k-1)\pi \leq x \leq k\pi,~k = 1,2,\cdots, n)\)と\(x\)軸で囲まれる部分の面積を\(S(k)\)とおくと，\[\displaystyle \int_0^{n\pi}e^{-x}|\sin x| dx= \sum_{k=1}^n S(k)\]となる．\((2)\)により，各山の面積は初項\(S(1)\)，公比\(e^{-\pi}\)の等比数列であるから，これはさらに\[\displaystyle \frac{S(1)(1-e^{-n\pi})}{1-e^{-\pi}}\]とかける．\(S(1)\)を求める．
\begin{align*}
\displaystyle S(1)&=\int_{0}^{\pi}f(x)dx\\
&=\int_{0}^{\pi} e^{-x}|\sin x| dx\\
&=\int_{0}^{\pi}e^{-x}\sin x dx\\
&=\left[\frac{-1}{2}\left(e^{-x}\sin x+e^{-x}\cos x\right)\right]_0^\pi\\
&=-\frac{1}{2}(-e^{-\pi}-1)\\
&=\frac{e^{-\pi}+1}{2}
\end{align*}したがって，求める極限は\[\frac{e^{-\pi}+1}{2}\frac{1-e^{-n\pi}}{1-e^{-\pi}}\xrightarrow{n\rightarrow \infty}\frac{e^{-\pi}+1}{2(1-e^{-\pi})}\]となる．【解答終】

\(f(x)=e^{-x}|\sin nx|\)などでも同様に「山の面積は等比数列」が成り立ちますので（調べてみましょう），多少状況が変化しても同様の方針で計算できます。

以下，\(a>c>0\)は議論の‘大前提’としておく．
\begin{align*}
&PF+PF’=2a\\
\Longleftrightarrow~&\sqrt{(x+c)^2+y^2}+\sqrt{(x-c)^2+y^2} = 2a\\
\Longleftrightarrow~&\sqrt{(x+c)^2+y^2} = 2a – \sqrt{(x-c)^2+y^2}\\
\Longleftrightarrow~&(x+c)^2+y^2 = \left( 2a – \sqrt{(x-c)^2+y^2} \right)^2 \land 2a – \sqrt{(x-c)^2 + y^2} \geq 0 \\
\Longleftrightarrow~&a\sqrt{(x-c)^2+y^2} = a^2 – cx \land 4a^2 \geq (x-c)^2 + y^2\\
\Longleftrightarrow~&a^2\left((x-c)^2+y^2\right) = (a^2 – cx)^2 \land a^2 – cx \geq 0 \land 4a^2 \geq (x-c)^2 + y^2\\
\Longleftrightarrow~&\frac{x^2}{a^2}+\frac{y^2}{a^2-c^2}=1 \land a^2 – cx \geq 0 \land 4a^2 \geq (x-c)^2 + y^2\\
\Longrightarrow~&\frac{x^2}{a^2}+\frac{y^2}{a^2-c^2}=1\tag{\(\ast\)}
\end{align*}
\((\ast)\)の十分性を示す．そのためには，次の二つの命題が示せればよい．
\begin{align*}
&\frac{x^2}{a^2}+\frac{y^2}{a^2-c^2}=1 \Longrightarrow a^2 – cx \geq 0 \tag{1}\\
&\frac{x^2}{a^2}+\frac{y^2}{a^2-c^2}=1 \Longrightarrow 4a^2 \geq (x-c)^2 + y^2 \tag{2}
\end{align*}
まず\((1)\)を証明する．まず仮定\(\frac{x^2}{a^2}+\frac{y^2}{a^2-c^2}=1\)により，\(\frac{x^2}{a^2} \leq 1\)が言える．すなわち\(-a \leq x \leq a\)．このとき，
\[a^2-cx \geq a^2-ca = a(a-c) > 0 \]
よって，\(a^2-cx > 0\)．これで\((1)\)が示された．

次に\((2)\)を証明する．まず仮定\(\frac{x^2}{a^2}+\frac{y^2}{a^2-c^2}=1\)により，\(\frac{y^2}{a^2-c^2} \leq 1 \Leftrightarrow y^2 \leq a^2 – c^2\)が言える．また，前半と同様にして\(\frac{x^2}{a^2}+\frac{y^2}{a^2-c^2}=1\)から\(-a \leq x \leq a\)が言えることにも注意する．以上の準備の下に，\((2)\)を示す．
\begin{align*}
(x-c)^2 + y^2 \leq &~(x-c)^2 + a^2-c^2\\
= &~x^2-2cx+a^2\\
\leq &~a^2-2cx+a^2\\
= &~2(a^2-cx)\\
\leq &~2(a^2+ca)\\
< &~2(a^2+a^2)=4a^2
\end{align*}
ゆえに，\((x-c)^2 + y^2 < 4a^2\)．これで\((2)\)も示された．

以上により\((\ast)\)の十分性，すなわち
\begin{align*}
\frac{x^2}{a^2}+\frac{y^2}{a^2-c^2}=1 \land a^2 – cx \geq 0 \land 4a^2 \geq (x-c)^2 + y^2&\\
\Longleftarrow~\frac{x^2}{a^2}+\frac{y^2}{a^2-c^2}=1&
\end{align*}
が言えた．よって，
\[PF+PF’=2a~\Longleftrightarrow~\frac{x^2}{a^2}+\frac{y^2}{a^2-c^2}=1\]
が得られる．

\(\ast\)　　　　\(\ast\)　　　　\(\ast\)

教科書では必要性だけを追っていき最後に「逆に，\(\frac{x^2}{a^2}+\frac{y^2}{a^2-c^2}=1\)を満たす点\(\mathrm{P}(x,y)\)は，\(PF+PF’=2a\)を満たす」としか書いておらず，なぜ逆が成り立つのかについては触れていません．

この軌跡を楕円と呼びます．

教科書では，この公式の下で，次のような問題と解答を用意しています．

\(x^2+1=u\)とおくと\(2xdx = du\)

\begin{align*}
\displaystyle \int x \sqrt{x^2+1}dx &= \frac{1}{2}\int \sqrt{x^2+1}\cdot 2x dx\\
\displaystyle &= \frac{1}{2}\int \sqrt{u} du=\cdots\\
\displaystyle &=\frac{1}{3}(x^2+1)\sqrt{x^2+1}+C
\end{align*}

引用元：『高等学校　数学Ⅲ』数研出版

置換してますね．

ところで，\(\int f(u) du\)って\(f(u)\)の原始関数なんだから，上の公式は
\begin{align*}
\displaystyle \int f(g(x))g'(x) dx&=\int f(u) du \quad\text{ただし，}g(x)=u\\
\displaystyle &=F(u) + C\quad\text{ただし，}g(x)=u\\
\displaystyle &=F(g(x)) + C\\
\end{align*}

と変形して，

とも書けますね．というか，これを公式としたほうが良くない…？そうすれば「被積分関数が\(f(g(x))g'(x)\)という形をしていれば，\(f(\quad)\)の原始関数を求めて，その’中身’である\(g(x)\)をそのまま放り込めばいい」という簡単な使い方に変わると思うんですが…．

あと教科書の解説だと全ッ然強調してないのですが，この公式が使えることにそもそもどうやって気付くのか？が実用（受験）上では極めて重要です．たとえこの公式を知識として持っていても気付かなければ使おうという発想に至りませんからね．気付くためのポイントは被積分関数に\(g(x)\)と\(g'(x)\)という二人がいるかどうか？です．この「\(g,~g’\)」が見つかったら，まずこの公式のタイプだと思って間違いないでしょう．そして見つかった\(g(x)\)と\(g'(x)\)のうち，\(g(x)\)を\(X\)などとおいて浮かび上がってくる関数が\(f(X)\)です．そしてその\(f(X)\)の原始関数（の１つ）さえ見つけらればこの積分計算はそれで終わりです．

上の例でやってみましょう．\(x^2+1\)と\(x\)の間にその\(g,~g’\)関係がありそうですね．でも惜しいことに\(x^2+1\)を微分すると\(2x\)です．今あるのは\(x\)だからちょっと違う．まあでも，係数の違いは微調整して\(x=\frac{1}{2}\cdot 2x\)と思っておけばいいでしょう．これで\(g(x)\)が見つかりました．これを\(X\)とおいてその部分を眺めてみましょう．すると\(\sqrt{X}=X^{\frac{1}{2}}\)となります．これが知りたかった\(f(X)\)です．あとはこれの原始関数（の１つ）を求めればいい．\[\frac{1}{\frac{1}{2}+1}X^{\frac{1}{2}+1}=\frac{2}{3}X^{\frac{3}{2}}\]
あとは\(\frac{2}{3}(\quad)^{\frac{3}{2}}\)にもともとあった\(g(x)=x^2+1\)を放り込んで\(\frac{1}{2}\cdot\frac{2}{3}(x^2+1)^{\frac{3}{2}}\)．たったこれだけで終了．置換などする必要がない．ちなみに先頭の\(\frac{1}{2}は\)先ほど\(g'(x)\)を\(\frac{1}{2} \cdot 2x\)と微調整しておいてときの\(\frac{1}{2}\)です．以上解答としてまとめると

\begin{align*}
\displaystyle \int x \sqrt{x^2+1}dx &= \frac{1}{2}\cdot\frac{2}{3}(x^2+1)^{\frac{3}{2}}+C\\
&= \frac{1}{3}(x^2+1)^{\frac{3}{2}}+C
\end{align*}

ほぼ一行で終わります．「\(f,g,g’\)」タイプにおいてすべきことは\(f(\quad)\)を見つけ出しその原始関数（の１つ）を求めるだけです．教科書のようにダラダラと置換してはいけません．

（高校生へ注意）この記事を読む際は，教科書の定積分の定義は忘れて読んで下さい．一旦無の状態に戻るのが理解のポイントです．

私たちは四角形の面積なら求められます．タテ\(\times\)ヨコ．さらにここから，三角形の面積やら台形の面積やらをも求められることになります．では，下のような曲線を含む図形Aの面積はどうやって求めればいいのでしょうか．というか，何を指して曲線を含む図形Aの「面積」とすればいいのでしょうか？

下図のような\(x\)軸，\(y=f(x)\)，\(x=a\)，\(x=b\)状況を仮定した上で，次のように考えてみます：

まず，図形を分割します．何個に分割してもいいのですが，ここでは\(n\)個に分割（等分でなくともよい）することにします．\[a=x_0<x_1<x_2<x_3<\cdots<x_{n-1}<x_{n}=b\]という分割です．

次に，これら\(n\)個の図形を，長方形に近似します．区間\([x_{i-1},~x_{i}]\)において「高さ」をとる\(x\)を\(\xi_i\)とします．区間\([x_{i-1},~x_{i}]\)上のどの点\(x\)を\(\xi_i\)とするかは任意です（ちなみに\(\xi\)はギリシャ文字で「グザイ」「クシー」などと読みます）．

これらの長方形の面積を求めます．例えば左から\(i\)番目の長方形の面積なら，横幅は\(x_{i}-x_{i-1}\)です．高さは\(f(\xi_i)\)です．したがって左から\(i\)番目の長方形の面積は
\[f(\xi_i)(x_{i+1}-x_i)\]
と書けます．さらに，\(x_{i+1}-x_i=\Delta x_i\)とおけば，
\[f(\xi_i)\Delta x_i\]
と書けます．これを\(n\)個寄せ集めるのですから，敷き詰めた長方形の面積の和は
\[\sum^{n}_{i=0}f(\xi_i)\Delta x_i\]
と表されることになります．これをリーマン和と呼びます．

この「リーマン和」をもってして図形Aの「面積」とするのはどうでしょうか？…それはちょっとマズイ気がします．なぜなら，図形Aとリーマン和とではスキマ（誤差）が大きすぎますから（下図参照）．

どうすればスキマ（誤差）は小さくなるでしょうか？各長方形の幅を小さくすれば，細長い長方形になって，スキマは小さくなります．当然，スキマは小さければ小さいほど，今私たちにとって欲しいものが正確に求まりそうな気がします．各長方形の幅を小さくするには，\(n\)を大きく，すなわち分割の数を大きくしてやればいいでしょう．

式で表すと，
\[\lim_{n\rightarrow \infty}\sum^{n}_{i=0}f(\xi_i)\Delta x_i\]
これなら，図形の「面積」と呼んでも差し支えなさそうです．そこで，この極限値を図形Ａの「面積」と定義し，「定積分」と名付け，記号\[\int^b_a f(x)dx\]で表すことにします．

\(:=\)は「左辺を右辺で定義する」という意味です．

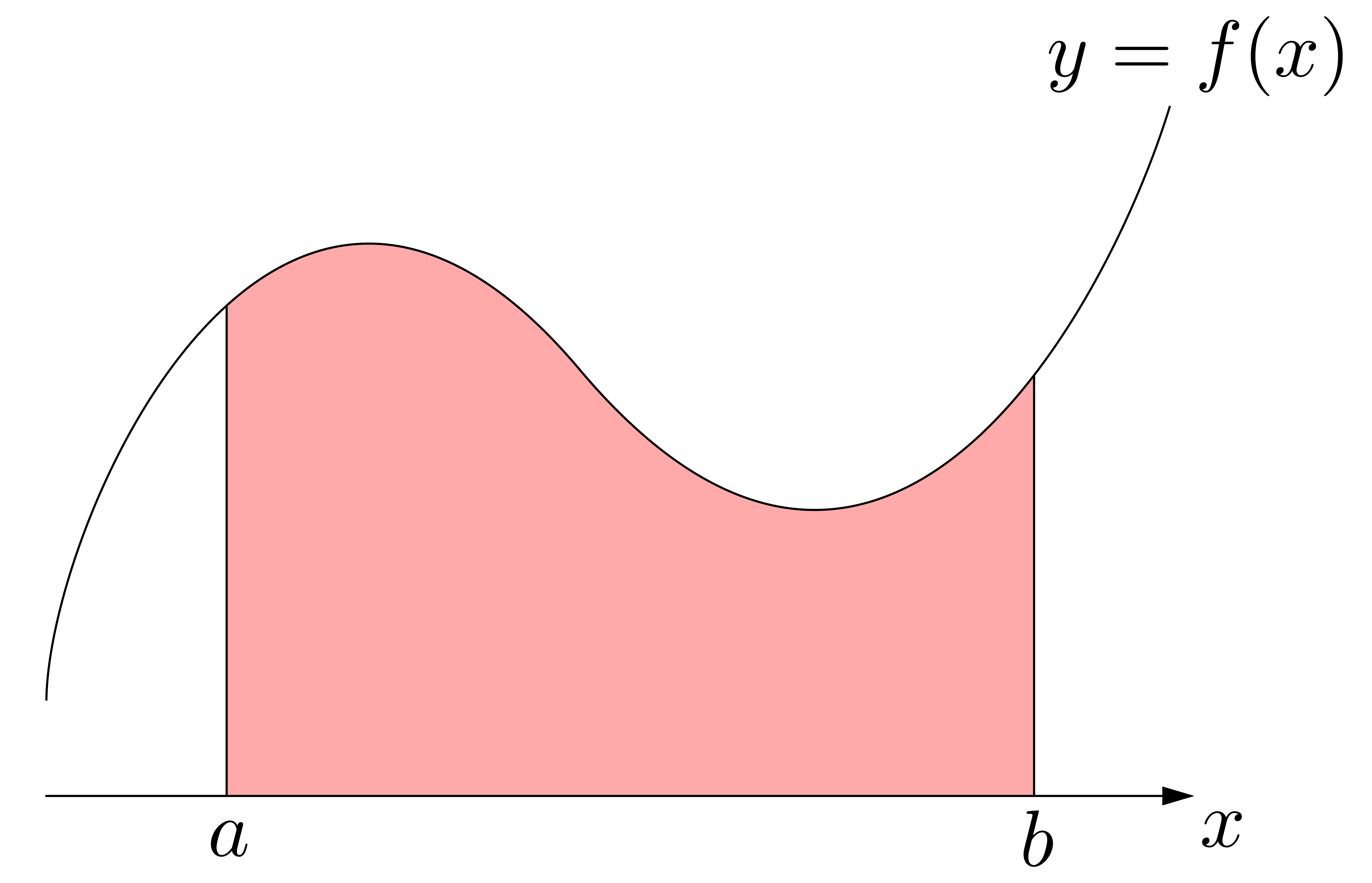
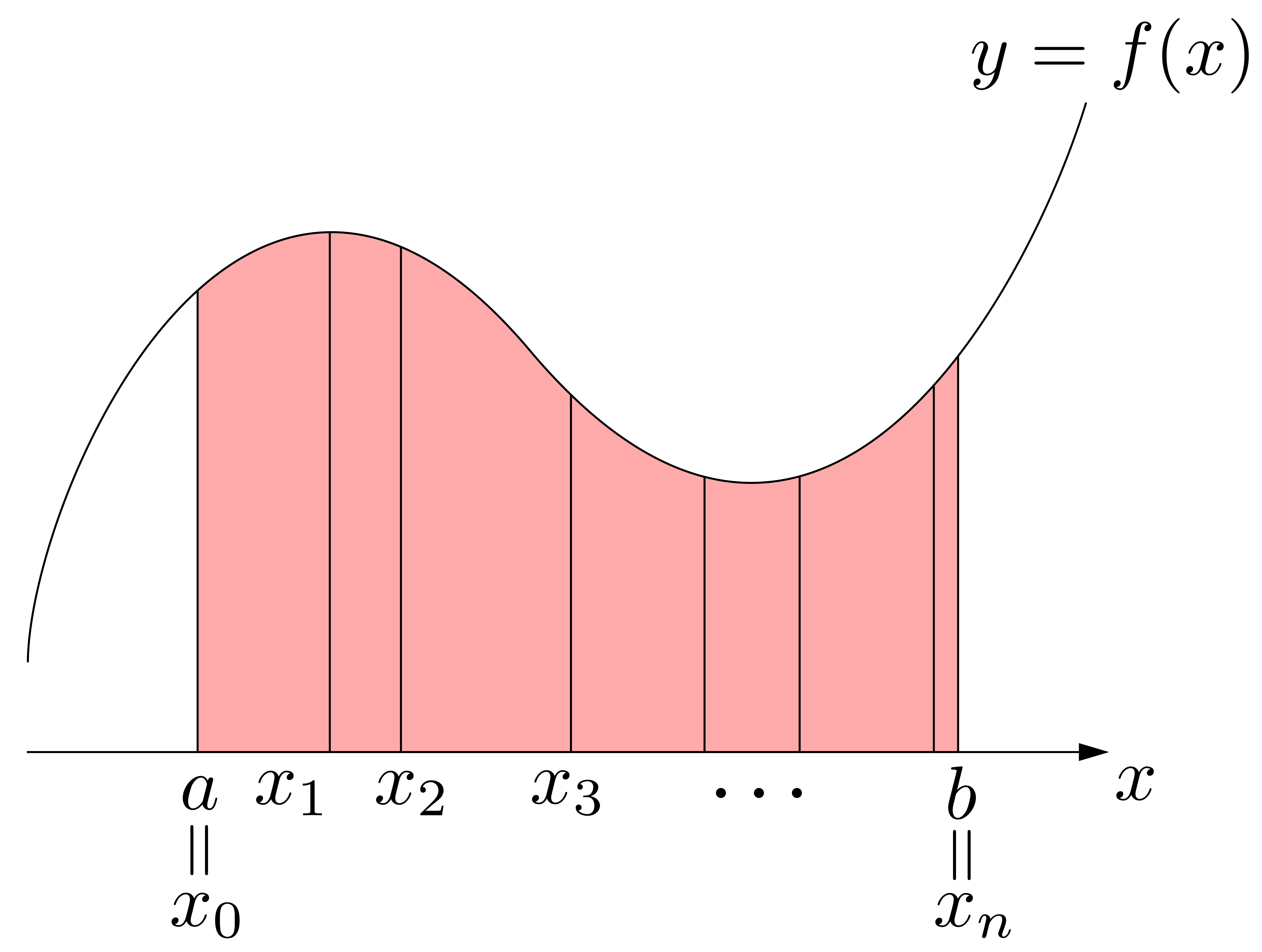
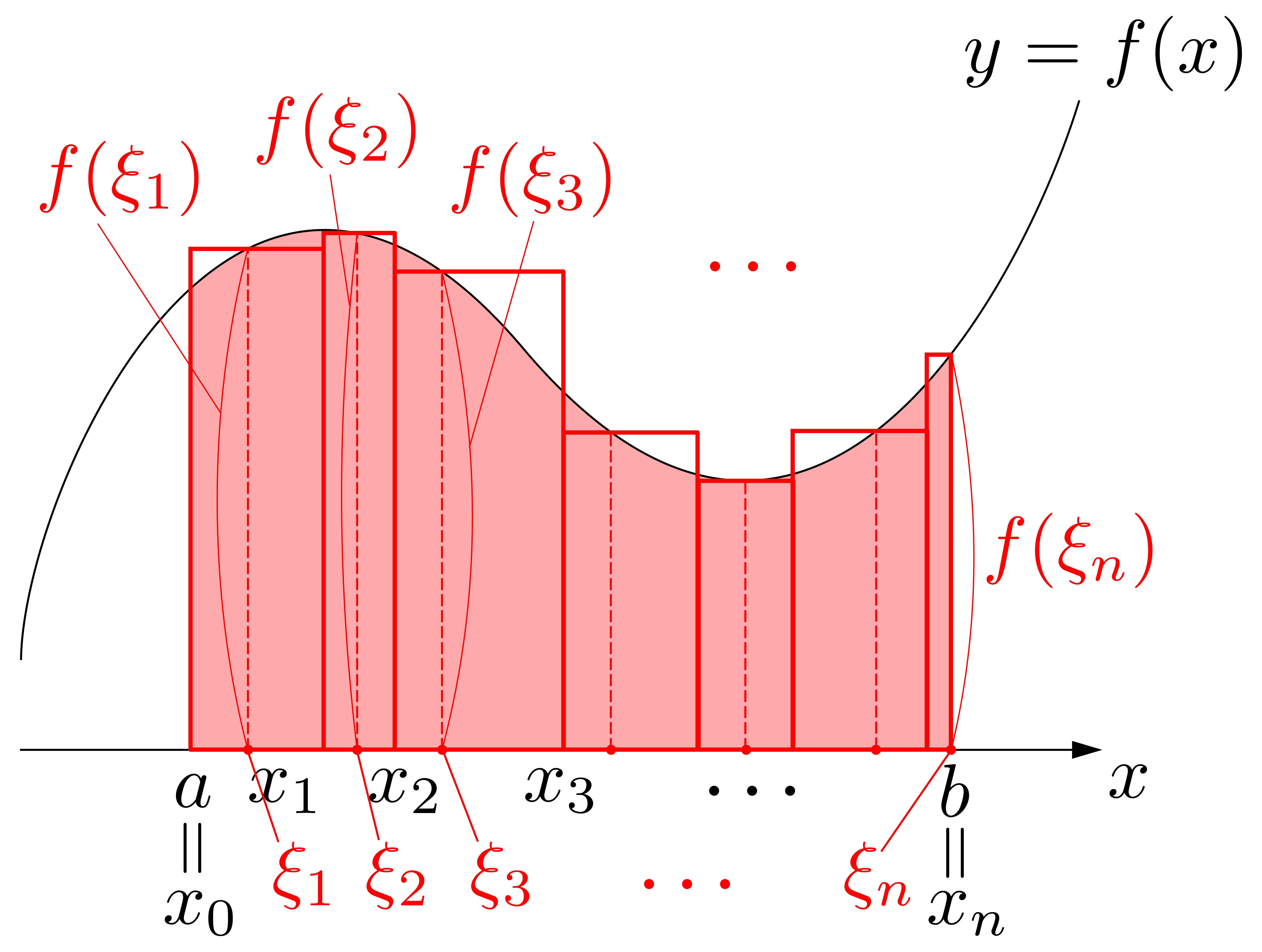
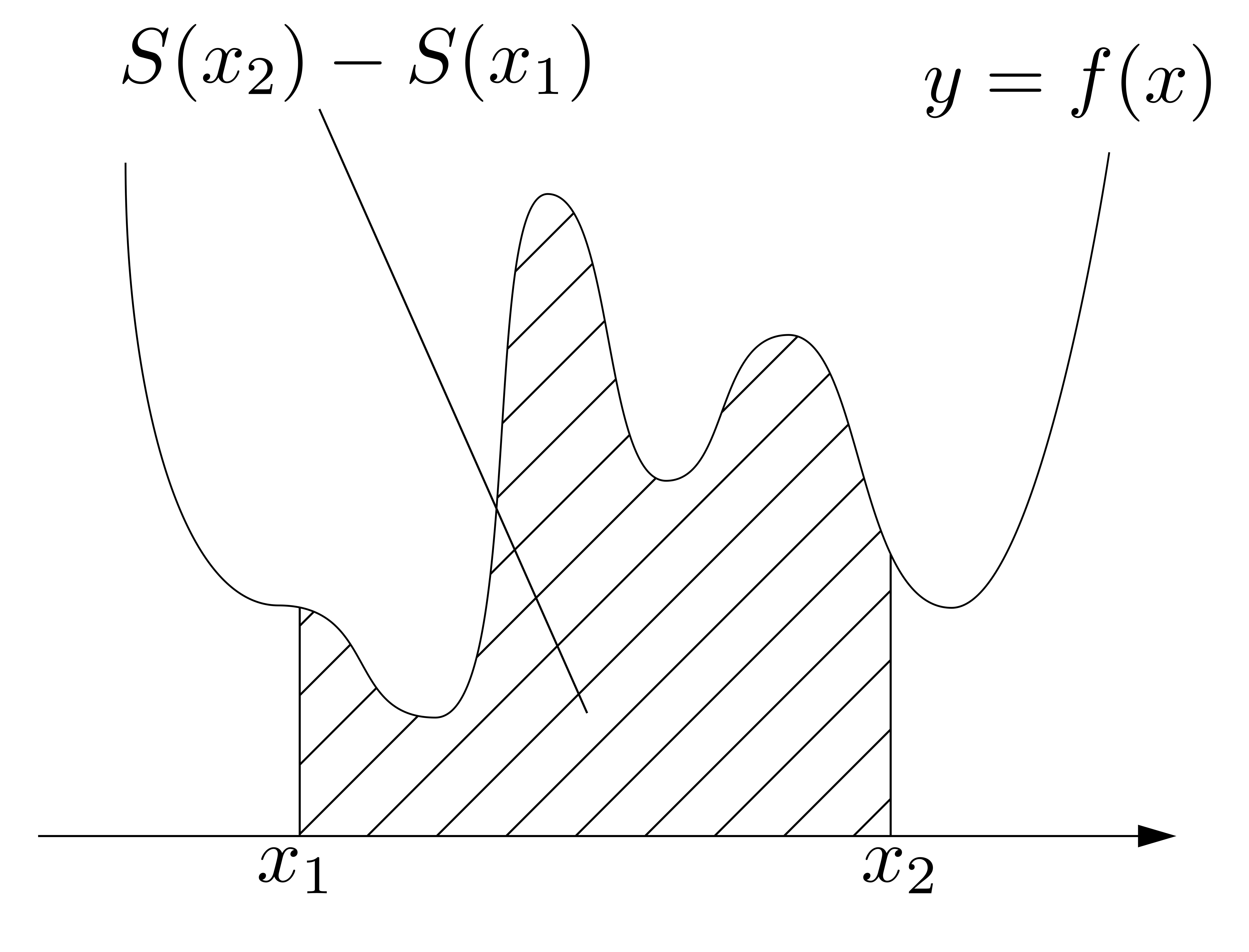
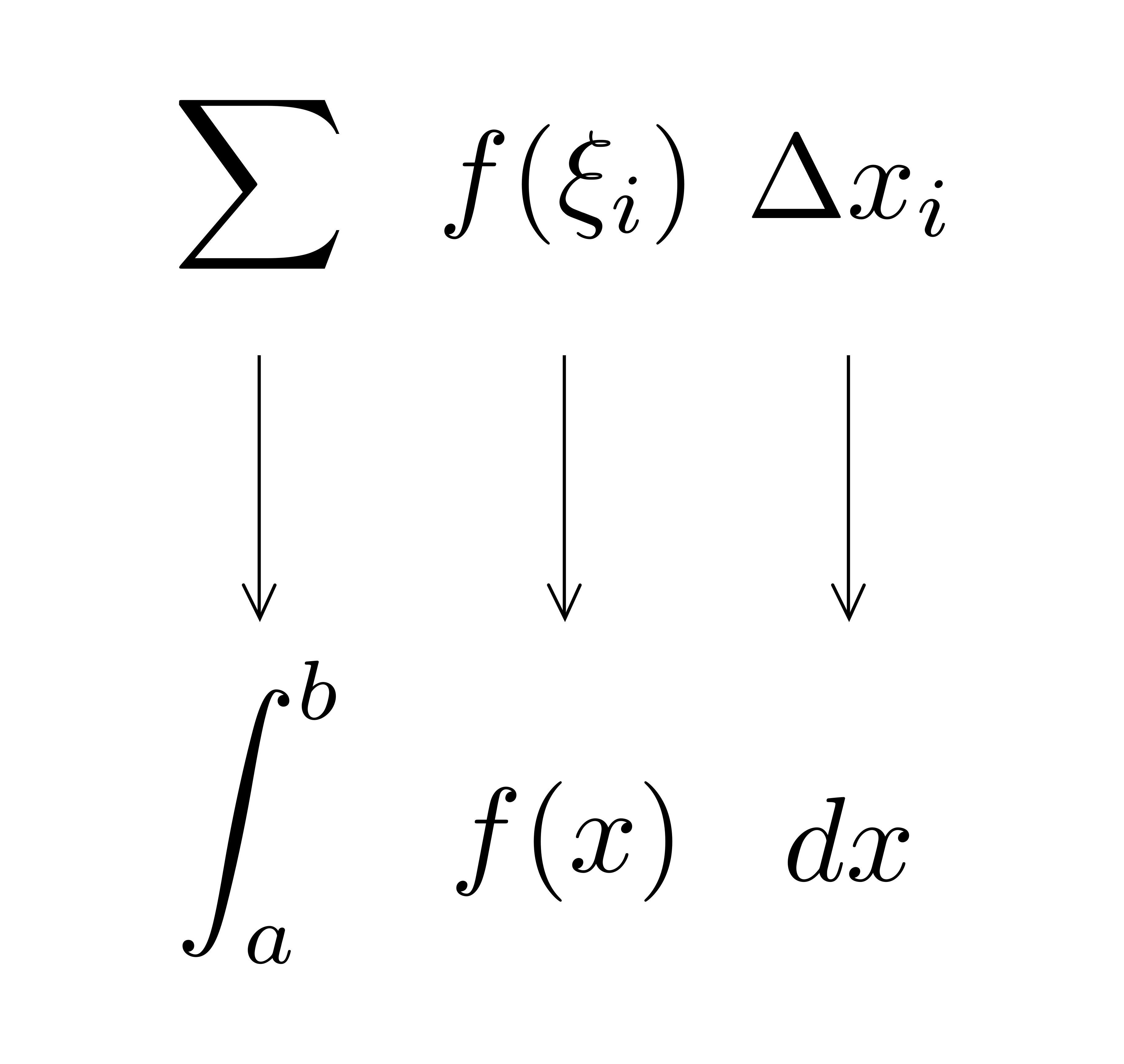以上を見ると，\(\displaystyle \int^b_a f(x)dx\)の\(\displaystyle \int\)や\(dx\)の「イメージ」が見えてきます．右図に示すように，\(\displaystyle \sum\)が\(\displaystyle \int\)に，\(\Delta x_i\)が\(dx\)と対応しているわけです．

ここで，\(\displaystyle \sum\ f(\xi_i)\Delta x_i\)の意味を思い出しましょう．\(f(\xi_i)\)が「タテ」，\(\Delta x_i\)が「ヨコ」を表すのでしたから，\(f(\xi_i)\times\Delta x_i\)は「長方形の面積」を意味し，その長方形の面積\(f(\xi_i)\Delta x_i\)を\(\displaystyle \sum\)する（足し加える），という意味でした．

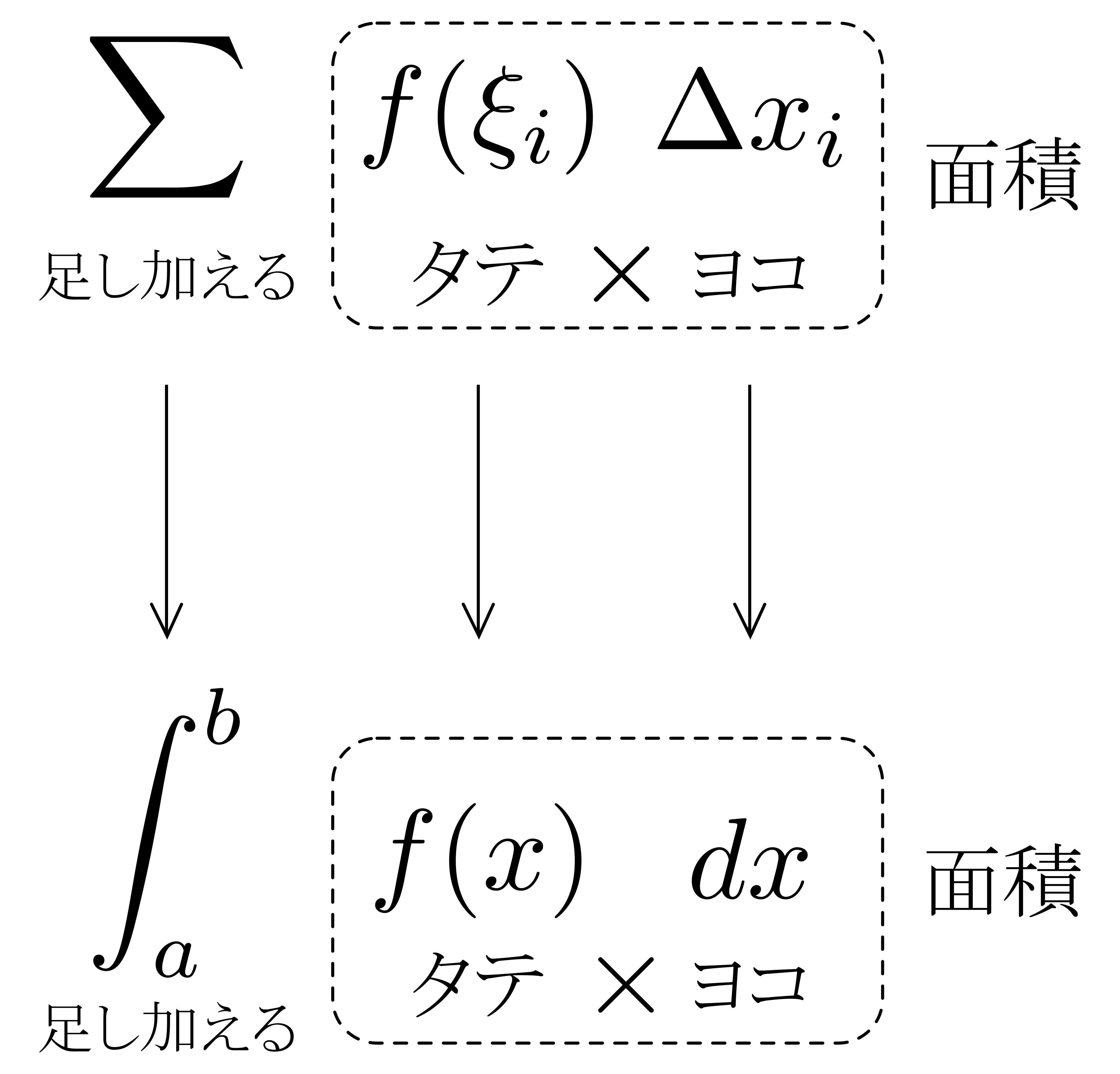以上を踏まえて\(\displaystyle \int^b_a f(x)dx\)を眺めると，これは「微小面積\(f(x)\times dx\)を\(\displaystyle \int\)したもの（連続的に足し加えたもの）」と読み取れることが分かります！

定積分を「リーマン和の極限」とみなす捉え方は，とても自然で，記号の導入も全く違和感がありません．さらに，右図に示した記号の解釈は，定積分の問題を扱う上で極めて重要な解釈になります．

次回はこの定積分の定義に従って図形の面積を計算してみます．すると，大きな問題に直面します…．

高校教科書では，定積分を次のように定義しています．

そして，数学Ⅱまたは数学Ⅲで積分を既習の人はこの定積分を計算することによって「面積が求まる」ということも知っていると思います．

しかし，ここでひとつ疑問．なぜ定積分で面積が求まるのでしょうか？定積分の定義は上に示したようにあくまで「原始関数の差を『定積分』と呼ぶことにしましょう」と言っているに過ぎず，「面積」云々には一切触れていません．つまり（定積分の「定義」から）「面積が求まる」ということが「定理」として得られるはずですが，その理由はどこにあるのでしょうか？その辺を理解しないままにただただ計算している人も多いのではないでしょうか．

調べてみましょう．

今，\(y=f(x),~x\leq k,~y=0\)で示される部分の面積を\(S(k)\)と表すことにします．

すると，\(y=f(x),~x=x_1,~x=x_2,~y=0\)で囲まれる部分の面積は，\[S(x_2)-S(x_1)\]で表されることになります．

この斜線部分の面積を評価することを考えます．斜線部分の面積\(S(x_2)-S(x_1)\)は，区間\([x_1,~x_2]\)の幅\(x_2-x_1\)を「ヨコ」，区間\([x_1,~x_2]\)で一番大きい\(y\)の値\(f(x_{max})\)を「タテ」としたときの長方形の面積\((x_2-x_1)f(x_{max})\)より小さく，区間\([x_1,~x_2]\)の幅\(x_2-x_1\)を「ヨコ」，区間\([x_1,~x_2]\)で一番小さい\(y\)の値\(f(x_{min})\)を「タテ」としたときの長方形の面積\((x_2-x_1)f(x_{min})\)よりも大きいと言えます（下図参照．一番大きい，または小さい\(y\)の値を取るときの\(x\)をそれぞれ\(x_{max},~x_{min}\)とおきました）．

したがって，以下の不等式が成り立ちます．
\[(x_2-x_1)f(x_{min})\leq S(x_2)-S(x_1)\leq (x_2-x_1)f(x_{max})\]
さらに，辺々を\(x_2-x_1\)で割ることで，
\[f(x_{min})\leq \frac{S(x_2)-S(x_1)}{x_2-x_1}\leq f(x_{max})\]
が得られます．

ここで，\(x_2\)を\(x_1\)に近づけてみます．すなわち，
\[\lim_{x_2\rightarrow x_1}f(x_{min})\leq \lim_{x_2\rightarrow x_1}\frac{S(x_2)-S(x_1)}{x_2-x_1}\leq \lim_{x_2\rightarrow x_1}f(x_{max})\]
まず中辺ですが，これは導関数の定義から\[S'(x_1)\]と書けます．

次に左辺と右辺について．\(x_2\)を\(x_1\)に近づけるというのは，区間\([x_1,x_2]\)の幅を縮めるということですから，図から\(f(x_{max}),~f(x_{min})\)はどちらも\(f(x_1)\)に近づくことが分かります（下図参照）．

すなわち，
\[\lim_{x_2\rightarrow x_1}f(x_{max})=\lim_{x_2\rightarrow x_1}f(x_{max})=f(x_1)\]

したがって，はさみうちの原理から
\[S'(x_1)=f(x_1)\]
が得られますが，この式は
\[S(x_1)=\text{\(f(x_1)\)の原始関数}\]
であることを示しています．添え字がちょっとうるさいので\(x_1\)を\(x\)に置き換えておきます．
\[S(x)=\text{\(f(x)\)の原始関数}\]
準備は整いました．定積分の定義\(\displaystyle \int^b_a f(x)dx=F(b)-F(a)\)を変形してみます．
\[
\begin{align}
\int^b_a f(x)dx=&F(b)-F(a)\\
=&\text{\(f(x)\)の原始関数}|_{x=b}-\text{\(f(x)\)の原始関数}|_{x=a}\tag{1}\\
=&S(x)|_{x=b}-S(x)|_{x=a}\tag{2}\\
=&S(b)-S(a)
\end{align}
\]
\((1)\)は定義の仮定：「\(F(x)=\text{\(f(x)\)の原始関数}\)」から，
\((2)\)は先に導いた式：「\(S(x)=\text{\(f(x)\)の原始関数}\)」によるものです．

結局，
\[\int^b_a f(x)dx=S(b)-S(a)\]
が得られますが，\(S(b)-S(a)\)は\(y=f(x),~x=a,~x=b,~y=0\)で囲まれた面積を表しますから，定積分すなわち原始関数の差は確かに面積を表すことが確認でしました．

以上により定積分で面積が求められることが一応納得はできました．しかしながら，この「納得」は上でみたように複雑で，お世辞にも「直観的」とは言えません．一般に求積問題は図形が絡むので視覚情報から解法に繋げていくことが多いのですが，その視覚情報を数式に落とし込むにはある種の「直観的」な理解が必要になってきます．教科書の定義のままでは直観的な理解が伴わないゆえに求積問題等ではうまく発想・立式ができず，ほとんど使い物になりません．数学が得意な人，これから得意にしたい人，あるいは将来的に数学を使う学部学科に進みたい人は違う角度で定積分というものを捉える（理解する）べきです．

次回，「定積分」を教科書とは違う角度から（リーマン和の極限として）再定義し，今度は逆に「定積分が原始関数の差である」ことを定理として導いてみようと思います．すなわち，教科書が「定積分とは原始関数の差である（定義）→定積分は面積である（定理）」という流れであったのに対し，逆に「定積分はリーマン和の極限（＝面積）である（定義）→定積分は原始関数の差である（定理）」という流れで定積分というものを捉え直します．この考え方自体がとりもなおさず受験数学における求積問題の肝にもなります．

（証明）

積の微分法より\[(F(x)g(x))’=f(x)g(x)+F(x)g'(x)\]
この式は「微分して\(f(x)g(x)+F(x)g'(x)\)になるような関数が，\(F(x)g(x)\)」ということですから，不定積分が原始関数を表すことを思い出すと\[F(x)g(x)=\int \big( f(x)g(x)+F(x)g'(x) \big)dx\]と書けます．不定積分の線形性より，
\[F(x)g(x)=\int f(x)g(x)dx+\int F(x)g'(x) dx\]
移項すると，\[\int f(x)g(x)dx=F(x)g(x)-\int F(x)g'(x) dx\]（証明終）

教科書等だと部分積分の公式は\[\int f'(x)g(x)dx=f(x)g(x)-\int f(x)g'(x) dx\]などと書かれていることが多いので，「まず被積分関数（の一部）を\(f'(x)\)の形にしてから公式を適用する」と認識されがちですが，その使い方はちょっと面倒だと思います．そうではなく，上のように\[\int f(x)g(x)dx=F(x)g(x)-\int F(x)g'(x) dx\]と認識しておけば，結局「片方\(f(x)\)の原始関数（の１つ）を求めて，もう片方\(g(x)\)を微分する」と読め，やるべきことが明解です．もちろん，やっていることは同じなんですがこんな地味なレベルでの認識の違いで覚えやすさ，計算のスピードが変わってくるので意外と大事です．

覚え方：代ゼミの荻野暢也先生の言葉をお借りすれば…「片方積分して，放っておかれたほう微分して引く積分」です！（僕はこの荻野先生の覚え方で覚えました＾＾；．部分積分するときは未だにこれを頭の中で唱えながら部分積分しています．おすすめです）