\[\exists s \exists t \left[s = \frac{2Y}{2-X} \land t = \frac{X}{2-X} \land s^2=4t \right]\]という主張の同値変形について見てみます.
【変形1】
\begin{align*}
&\exists s \exists t \left[s = \frac{2Y}{2-X} \land t = \frac{X}{2-X} \land s^2=4t \right]&(0)\\
\Longleftrightarrow~&\exists s \exists t \left[s = \frac{2Y}{2-X} \land t = \frac{X}{2-X} \land \frac{4Y^2}{(2-X)^2}=\frac{4X}{2-X}\right]&(1)\\
\Longleftrightarrow~&\exists s \exists t \left[s = \frac{2Y}{2-X} \land t = \frac{X}{2-X} \land Y^2=X(2-X) \land X \neq 2 \right]&(2)\\
\Longleftrightarrow~&\exists s \exists t \left[s = \frac{2Y}{2-X} \land t = \frac{X}{2-X} \right] \land Y^2=X(2-X) \land X \neq 2&(3)\\
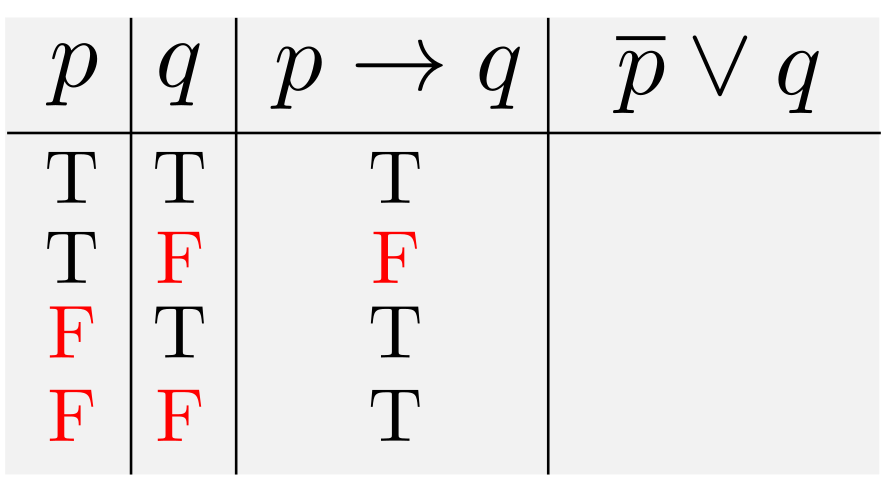
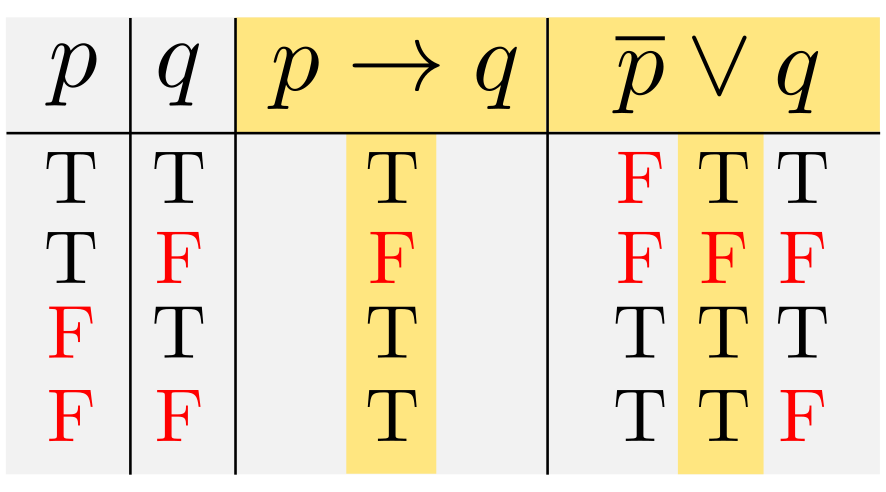
\Longleftrightarrow~&X \neq 2 \land Y^2=X(2-X) \land X \neq 2&(4)\\
\Longleftrightarrow~&Y^2=X(2-X) \land X \neq 2&(5)\\
\Longleftrightarrow~&(X-1)^2+Y^2=1 \land X \neq 2
\end{align*}
\((2)\)は\(\frac{4Y^2}{(2-X)^2}=\frac{4X}{2-X} \Longleftrightarrow Y^2=X(2-X) \land X \neq 2\)
\((3)\)は\(Y^2=X(2-X) \land X \neq 2\)が変数\(s,t\)を含まないので,\(\exists s\exists t\)の支配域を変更することができるから
\((4)\)は\(\exists s \exists t \left[s = \frac{2Y}{2-X} \land t = \frac{X}{2-X} \right] \Longleftrightarrow X \neq 2\)より
\((5)\)は
\[p \land q \Leftrightarrow q \land p,\quad p \land p \Leftrightarrow p\]
によります(いずれも真理値表から明らか)
【変形2】
\begin{align*}
&\exists s \exists t \left[s = \frac{2Y}{2-X} \land t = \frac{X}{2-X} \land s^2=4t \right]&(0)’\\
\Longleftrightarrow~&\exists s \left[ \exists t \left[s = \frac{2Y}{2-X} \land t = \frac{X}{2-X} \land s^2=4t\right]\right] &(1)’\\
\Longleftrightarrow~&\exists s \left[s = \frac{2Y}{2-X} \land \exists t\left[ t = \frac{X}{2-X} \land s^2=4t\right]\right] &(2)’\\
\Longleftrightarrow~&\exists s \left[s = \frac{2Y}{2-X} \land s^2=\frac{4X}{2-X}\right] &(3)’\\
\Longleftrightarrow~&\left(\frac{2Y}{2-X}\right)^2=\frac{4X}{2-X} &(4)’\\
\Longleftrightarrow~&Y^2=X(2-X) \land X \neq 2&(5)’\\
\Longleftrightarrow~&(X-1)^2+Y^2=1 \land X \neq 2
\end{align*}
\((1)’\)はそもそも\(\exists s\left[ \exists t[p(s,t)]\right]\)の略記が\(\exists s \exists t[p(s,t)]\)だから
\((2)’\)は支配域の変更.\((2)\)と同じ
\((3)’\)は\(\exists t\)の処理
\((4)’\)は\(\exists s\)の処理
\((5)’\)は\((1)\)と同様の同値変形によります
\((0)’\)から\(~(4)’\)までの同値変形はこのように書くと厳ついですがやってることは結局\(s,t\)の消去です.通常は\((0)’\)から\((4)’\)まで一気に一行で処理してしまうところだと思います.
\((0)\)から\((1)\)への変形と\((0)’\)から\((4)’\)への変形に違いに注意しましょう(詳しくはこの記事にて.関連:「『存在する』の扱い」,「連立方程式の解法は…『文字を減らす』方針?」).文字を「消去する」ことを正しく認識していないとこういう箇所で間違えてしまうので注意.
【変形1】【変形2】いずれにしても同じ結論です.途中のアプローチが違えど,論理式を正しく扱いすれば必然的に同じ結論が得られる,ということでした.