タグ: 数学Ⅱ

\(\rm(i\hspace{-.08em}i\hspace{-.08em}i)\)のとき．
\begin{align*}
&\text{円と放物線が接する}\\
\overset{def}{\Longleftrightarrow}~&\text{円と放物線が\(1\)点\(\mathrm{T}\)を共有し，点\(\mathrm{T}\)における両者の接線が一致する}\\
\Longleftrightarrow~&\text{放物線上の点\(\mathrm{T}\)を通り，その点における接線に垂直な直線が円の中心を通る}\\
\end{align*}
であることに着目する．\(\mathrm{T}(t,t^2+k)\)とおく．放物線上の点\(\mathrm{T}\)を通り，その点における接線に垂直な直線の方程式は\((t^2+k)’=2t\)であることから
\[y-(t^2+k)=-\frac{1}{2t}(x-t)\]
とかける．これが原点を通るから，
\[0-(t^2+k)=-\frac{1}{2t}(0-t) \Longleftrightarrow t^2=-k-\frac{1}{2}\]
これを満たす\(t\)が存在すればよいから（点\(\mathrm{T}\)は円上の点であることにも注意して），
\begin{align*}
&\exists t\begin{cases}t^2+(t^2+k)^2=4 \\ t^2=-k-\frac{1}{2}\end{cases}\\
\Longleftrightarrow~& \exists t\begin{cases}\left(-k-\frac{1}{2}\right)+\frac{1}{4}=4 \\ t^2=-k-\frac{1}{2}\end{cases}\\
\Longleftrightarrow~& \exists t\begin{cases}k=-\frac{17}{4}\\ t^2=-k-\frac{1}{2}\end{cases}\\
\Longleftrightarrow~& \exists t\left[k=-\frac{17}{4} \land t^2=\frac{15}{4}\right]\\
\Longleftrightarrow~& k=-\frac{17}{4} \land \exists t\left[t^2=\frac{15}{4}\right]\\
\Longleftrightarrow~& k=-\frac{17}{4}
\end{align*}

「円と放物線」の定番問題です．多くの解答では「重解条件」を用いていますが，どこか気持ち悪い．「重解条件」を使わない解法について見てみます．

\((2)\)別解

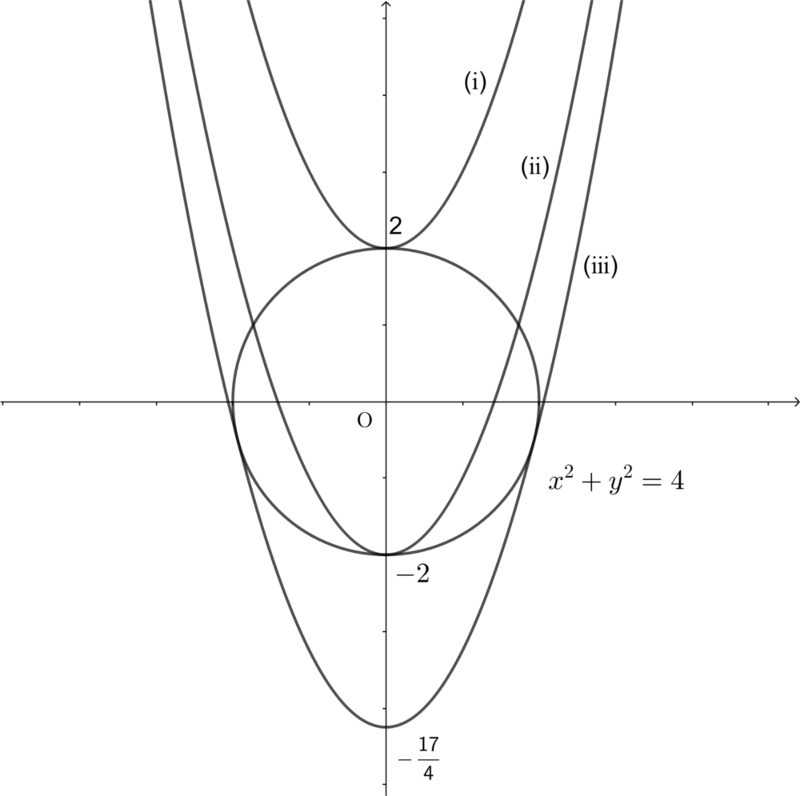
図により，
\[\text{接する}~\Longleftrightarrow \rm(\hspace{.18em}i\hspace{.18em})\text{または}\rm(\hspace{.08em}ii\hspace{.08em})\text{または}\rm(i\hspace{-.08em}i\hspace{-.08em}i)\]である．

\(\rm(\hspace{.18em}i\hspace{.18em})\)のとき，図より明らかに\(k=2\)．逆も成り立つ．

\(\rm(\hspace{.08em}ii\hspace{.08em})\)のとき，図より明らかに\(k=-2\)．逆も成り立つ．

\(\rm(i\hspace{-.08em}i\hspace{-.08em}i)\)のとき．
\(y=x^2+k\)上の点を\(P(s,s^2+k)\)とおく．線分\(OP\)を調べる．
\begin{align*}
OP^2=&s^2+(s^2+k)^2\\
=&t+(t+k)^2&(s^2=t\text{とおいた})\\
=&t^2+(2k+1)t+k^2\\
=&\left(t+k+\frac{1}{2}\right)^2-k-\frac{1}{4}&(t\geq 0)\\
\end{align*}
図より\(k<-2\)であるから\[-k-\frac{1}{2} > \frac{3}{2}\]
であることに注意すると，\(OP^2\)の最小値は\(-k-\frac{1}{4}\)．これが円の半径\(2\)と一致するとき，かつそのときに限り円と放物線は\(\rm(i\hspace{-.08em}i\hspace{-.08em}i)\)のように接する．したがって
\[\sqrt{-k-\frac{1}{4}}=2\Longleftrightarrow k=-\frac{17}{4}\]
以上により求める条件は\(k=\pm 2\)または\(k=-\frac{17}{4}\)となる．

\(\ast\)　　　　\(\ast\)　　　　\(\ast\)

（\(\rm(i\hspace{-.08em}i\hspace{-.08em}i)\)の別解はこちら）

という定番の問題についてみてみます．これは\(x+y=u,xy=v\)とおいたあと，「\(x,y\)が実数」という条件を\(u,v\)に反映させるのがポイントなのでした．すなわち，\(t^2-ut+v=0\)の判別式を\(\geq 0\)とすることにより
\[u^2-4v \geq 0\]
この不等式に注意しながら\(x+y+xy\)の最大値・最小値を調べる，という流れが定石でした（虎は死んで皮を残す，人は死んで名を残す，文字は死んで変域を残す…）．この，\(u^2-4v \geq 0\)を得る流れは論理的にはどうなっているのか，調べてみます．

解答
\begin{align*}
&\text{\(x+y+xy\)が\(k\)という値をとる}\\
\Longleftrightarrow~&\exists x \exists y[x+y+xy=k \land 2x^2+3xy+2y^2=1]\\
\Longleftrightarrow~&\exists x \exists y \left[x+y+xy=k \land 2x^2+3xy+2y^2=1 \land \exists u \exists v \begin{cases}x+y=u\\xy=v\end{cases}\right]\\
\Longleftrightarrow~&\exists x \exists y \exists u \exists v\left[x+y+xy=k \land 2(x+y)^2-xy=1 \land \begin{cases}x+y=u\\xy=v\end{cases}\right]\\
\Longleftrightarrow~&\exists x \exists y \exists u \exists v\left[u+v=k \land 2u^2-v=1 \land \begin{cases}x+y=u\\xy=v\end{cases}\right]\\
\Longleftrightarrow~&\exists u \exists v\left[u+v=k \land 2u^2-v=1 \land \exists x \exists y \begin{cases}x+y=u\\xy=v\end{cases}\right]\tag{\(\ast\)}
\end{align*}
ここで，
\begin{align*}
&\exists x \exists y \begin{cases}x+y=u\\xy=v\end{cases}\\
\Longleftrightarrow~&\exists x \exists y \begin{cases}x+y=u\\ \frac{1}{4}((x+y)^2-(x-y)^2)=v\end{cases}\\
\Longleftrightarrow~&\exists x \exists y \begin{cases}x+y=u \\ (x-y)^2=u^2-4v\end{cases}\\
\Longleftrightarrow~&\exists x \exists y \begin{cases}x+y=u \\ |x-y|=\sqrt{u^2-4v}\end{cases}\\
\Longleftrightarrow~&\exists x \exists y \begin{cases}y=u-x \\ (x-y=\sqrt{u^2-4v} \land x-y \geq 0 ) \lor (y-x=\sqrt{u^2-4v} \land x-y < 0 )\end{cases}\\ \Longleftrightarrow~&\exists x \left[\left(x=\frac{1}{2}\left(u+\sqrt{u^2-4v}\right) \land x \geq \frac{u}{2} \right) \lor \left(x=\frac{1}{2}\left(u-\sqrt{u^2-4v}\right) \land x < \frac{u}{2} \right)\right]\\ \Longleftrightarrow~&\frac{1}{2}\left(u+\sqrt{u^2-4v}\right) \geq \frac{u}{2} \lor \frac{1}{2}\left(u-\sqrt{u^2-4v} \right) < \frac{u}{2} \\ \Longleftrightarrow~&\sqrt{u^2-4v} \geq 0 \lor \sqrt{u^2-4v} < 0\\ \Longleftrightarrow~&\sqrt{u^2-4v} \geq 0\\ \Longleftrightarrow~&u^2-4v \geq 0\\ \end{align*} であるから，
\begin{align*}
(\ast)\Longleftrightarrow~&\exists u \exists v\left[u+v=k \land v=2u^2-1 \land u^2-4v \geq 0\right]\\
\Longleftrightarrow~&\exists u \left[u+(2u^2-1)=k \land u^2-4(2u^2-1) \geq 0\right]\\
\Longleftrightarrow~&\exists u \left[k = 2u^2+u-1 \land -\frac{2}{\sqrt{7}} \leq u \leq \frac{2}{\sqrt{7}}\right]\\
\Longleftrightarrow~&-\frac{9}{8} \leq u \leq \frac{1}{7}+\frac{2}{\sqrt{7}}
\end{align*}
ゆえに，最大値\(\displaystyle \frac{1}{7}+\frac{2}{\sqrt{7}}\)，最小値\(\displaystyle -\frac{9}{8}\).

\(\ast\)　　　　\(\ast\)　　　　\(\ast\)

「ここで，～であるから」までがいわゆる「実数の存在条件」の処理です．前回の「\(m^2<\frac{1}{12}\)を満たす実数の存在条件は～」と同じ考え方で導出してみました．

とある軌跡の問題の模範解答に関して次のような質問がありました．

模範解答では，\(X=\frac{16m^2}{4m^2+1}\)を得たのち
\[\text{「\(m^2<\frac{1}{12}\)を満たす実数の存在条件は\(0 \leq m^2<\frac{1}{12}\)だから，\(0 \leq X <1\)」}\]
とあるが，これは論理的にはどのように導いたのか？

模範解答だとたしかに何をやっているのか，というか何をいっているのかよくわかりません．

そこで論理式で考えます．模範解答の論理の流れはおそらくは以下です（代入法による解答との分岐点は\((1)\)からです）：

\begin{align*}
&\exists m \left[X=\frac{16m^2}{4m^2+1} \land Y=m(X-4)\land m^2<\frac{1}{12}\right]\\
\Longleftrightarrow~&\exists m\left[X=\frac{16m^2}{4m^2+1} \land Y=m(X-4)\land m^2<\frac{1}{12} \land (X=4 \lor X \neq 4)\right]\\
\Longleftrightarrow~&\exists m\left[\left(X=\frac{16m^2}{4m^2+1} \land Y=m(X-4)\land 0\leq m^2<\frac{1}{12} \land X=4 \right)\right.\\
&\lor \left.\left(X=\frac{16m^2}{4m^2+1} \land Y=m(X-4)\land m^2<\frac{1}{12} \land X \neq 4\right)\right]\\
\Longleftrightarrow~&\exists m\left[X=\frac{16m^2}{4m^2+1} \land m=\frac{Y}{X-4}\land m^2<\frac{1}{12} \land X \neq 4\right]\tag{0}\\
\Longleftrightarrow~&\exists m\left[X=\frac{16m^2}{4m^2+1} \land m=\frac{Y}{X-4}\land m^2<\frac{1}{12} \land X \neq 4 \land \exists t\geq 0 [t=m^2]\right]\tag{1}\\
\Longleftrightarrow~&\exists m\left[X=\frac{16m^2}{4m^2+1} \land m=\frac{Y}{X-4}\land m^2<\frac{1}{12} \land X \neq 4 \land \exists t[t\geq 0 \land t=m^2]\right]\tag{2}\\
\Longleftrightarrow~&\exists m \exists t\left[X=\frac{16m^2}{4m^2+1} \land m=\frac{Y}{X-4}\land m^2<\frac{1}{12} \land X \neq 4 \land t \geq 0 \land t=m^2\right]\tag{3}\\
\Longleftrightarrow~&\exists m \exists t\left[X=\frac{16t}{4t+1} \land m=\frac{Y}{X-4}\land t<\frac{1}{12} \land X \neq 4 \land t \geq 0 \land t=m^2\right]\tag{4}\\
\Longleftrightarrow~&\exists t\left[t=\frac{1}{4}\left(\frac{X}{4-X}\right) \land 0\leq t<\frac{1}{12} \land X \neq 4 \land t=\left(\frac{Y}{X-4}\right)^2\right]\tag{5}\\
\Longleftrightarrow~&0\leq \frac{1}{4}\left(\frac{X}{4-X}\right)<\frac{1}{12} \land X \neq 4 \land \frac{1}{4}\left(\frac{X}{4-X}\right)=\left(\frac{Y}{X-4}\right)^2\tag{6}\\
\Longleftrightarrow~&\frac{(X-2)^2}{4}+Y^2 = 1 \land 0 \leq X < 1 \land X \neq 4 \\
\Longleftrightarrow~&\frac{(X-2)^2}{4}+Y^2 = 1 \land 0 \leq X < 1
\end{align*}

\((0)\)ここまでこれと同じ
\((1)\)恒真条件\(\exists t \geq 0 [t=m^2]\)の追加．\(\exists m\)の支配域の下で考えているので，当然\(m^2\)すなわち\(0\)以上の\(t\)が存在しますから，恒真条件です．
\((2)\)略記の書き直し
\((3)\)\(\exists t\)の支配域の変更．自分\((t=m^2)\)以外はどれも変数\(t\)を含んでいないのでいちばん外側に追い出せます．
\((4)\)代入法（\(m^2\)に\(t\)を代入）
\((5)\)\(\exists m\)の処理
\((6)\)\(\exists t\)の処理

こうしてみると，模範解答での「（\(X=\frac{16m^2}{4m^2+1}\)において）\(m^2<\frac{1}{12}\)を満たす実数の存在条件は\(0 \leq m^2<\frac{1}{12}\)だから，\(0 \leq X <1\)」とは，厳密には以下のような操作を指して言っているのだと分かります：

• • \(m^2\)を\(t\)とおき\(\left((0) \Leftrightarrow (1)\right)\)，
  • 支配域の変更を経て\(\left((3)\right)\)，
  • 代入法により\(X=\frac{16t}{4t+1}\left(\Leftrightarrow t=\frac{1}{4}\left(\frac{X}{4-X}\right)\right)\)と（★）\(0\leq t<\frac{1}{12}\)が出現するわけですが\(\left((4)\right)\)，
  • 前者は\(t\)についての１次式ですから，\(\exists t\)により\(t\)を同値変形として「消去」できて，\(\left((5) \Leftrightarrow (6)\right)\)
  • 結果，（★★）同値性を保ったまま\(0 \leq X < 1\)が得られる．

模範解答にある
\[\text{「\(m^2<\frac{1}{12}\)を満たす実数の存在条件は\(0 \leq m^2<\frac{1}{12}\)だから，」}\]
に対応する部分が（★），そして
\[\text{「\(0 \leq X <1\)」}\]
に対応する部分が（★★），であろうとおそらくは考えられます．…確かに，このような内容になると「端折る」ことも必要になってくるのかもしれません．

他方，次のような「置き換え」をしない変形も考えられます．

（別解釈）
\begin{align*}
&\exists m \left[X=\frac{16m^2}{4m^2+1} \land Y=m(X-4)\land m^2<\frac{1}{12}\right]\\
\Longleftrightarrow~&\exists m\left[X=\frac{16m^2}{4m^2+1} \land Y=m(X-4)\land m^2<\frac{1}{12} \land (X=4 \lor X \neq 4)\right]\\
\Longleftrightarrow~&\exists m\left[\left(X=\frac{16m^2}{4m^2+1} \land Y=m(X-4)\land m^2<\frac{1}{12} \land X=4 \right)\right.\\
&\lor \left.\left(X=\frac{16m^2}{4m^2+1} \land Y=m(X-4)\land m^2<\frac{1}{12} \land X \neq 4\right)\right]\\
\Longleftrightarrow~&\exists m\left[X=\frac{16m^2}{4m^2+1} \land m=\frac{Y}{X-4}\land m^2<\frac{1}{12} \land X \neq 4\right] \tag{0}\\
\Longleftrightarrow~&\exists m\left[m^2=\frac{1}{4}\left(\frac{X}{4-X}\right)\land m=\frac{Y}{X-4}\land m^2<\frac{1}{12} \land X \neq 4 \right] \tag{1}\\
\Longleftrightarrow~&\exists m \left[m^2=\frac{1}{4}\left(\frac{X}{4-X}\right) \land m=\frac{Y}{X-4}\land \frac{1}{4}\left(\frac{X}{4-X}\right)<\frac{1}{12} \land X \neq 4 \right]\tag{2}\\
\Longleftrightarrow~&\left(\frac{Y}{X-4}\right)^2=\frac{1}{4}\left(\frac{X}{4-X}\right) \land \frac{1}{4}\left(\frac{X}{4-X}\right)<\frac{1}{12} \land X \neq 4 \tag{3}\\
\Longleftrightarrow~&\frac{(X-2)^2}{4}+Y^2 = 1 \land (X < 1 \lor 4 < X) \land X \neq 4\\
\Longleftrightarrow~&\left(\frac{(X-2)^2}{4}+Y^2 = 1 \land X \neq 4 \land X < 1 \right) \lor \left( \frac{(X-2)^2}{4}+Y^2 = 1\land X \neq 4 \land 4 < X \right) \\
\Longleftrightarrow~&\frac{(X-2)^2}{4}+Y^2 = 1 \land X \neq 4 \land X < 1 \tag{\(\ast\)}\\
\Longleftrightarrow~&\frac{(X-2)^2}{4}+Y^2 = 1 \land 0 \leq X < 1 \tag{\(\ast\)}
\end{align*}

\((1)\)は第一式を\(m^2\)について解いた
\((2)\)代入法
\((3)\)\(\exists m\)の処理

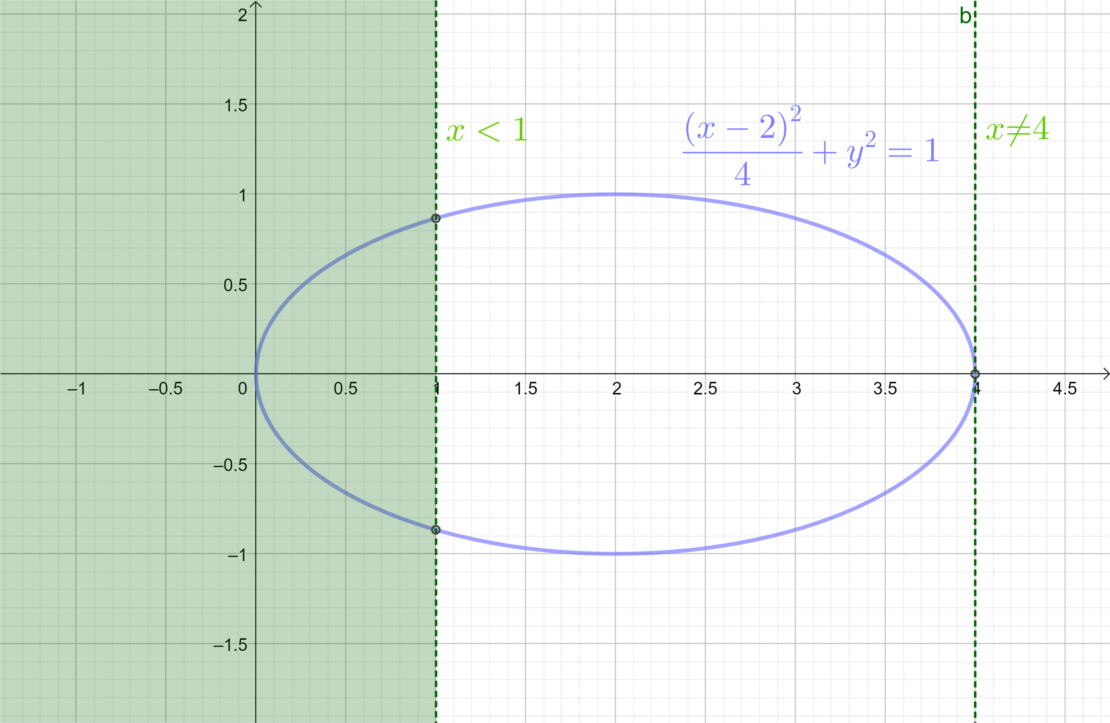
\((\ast)\)は下図による．

数学Ⅱ教科書の「軌跡と領域」における最後に登場する中ボス的な有名問題です．いわゆる「線型計画法」によって解く問題ですね．「領域を描いて～直線がその領域に触れる範囲内で切片が最大・最小のものを答えて～」みたいなやつ．

これを教科書のように絵に頼らず，論理式で記述してみます．

解答

\begin{align*}
&x+yがkという値をとる\\
\Longleftrightarrow~& \exists x \exists y [x+y=k \land x \geq 0 \land y \geq 0 \land 2x+y \leq 8 \land 2x+3y \leq 12]\tag{1}\\
\Longleftrightarrow~& \exists x \exists y[y=k-x \land x \geq 0 \land y \geq 0 \land 2x+y \leq 8 \land 2x+3y \leq 12]\tag{\(\ast\)}\\
\Longleftrightarrow~& \exists x [x \geq 0 \land k-x \geq 0 \land 2x+(k-x) \leq 8 \land 2x+3(k-x) \leq 12\tag{2}]\\
\Longleftrightarrow~& \exists x [x \geq 0 \land k \geq x \land x \leq 8-k \land 3k-12 \leq x]\\
\Longleftrightarrow~& \exists x [(x \geq 0 \land k \geq x \land x \leq 8-k \land 3k-12 \leq x)\land (3k-12<0 \lor 0 \leq 3k-12)]\tag{3}\\
\Longleftrightarrow~& \exists x [(x \geq 0 \land k \geq x \land x \leq 8-k \land 3k-12 \leq x \land 3k-12<0) \\
&\lor (x \geq 0 \land k \geq x \land x \leq 8-k \land 3k-12 \leq x \land 0 \leq 3k-12)]\tag{4}\\
\Longleftrightarrow~& \exists x [x \geq 0 \land k \geq x \land x \leq 8-k \land 3k-12 \leq x \land 3k-12<0] \\
&\lor \exists x[x \geq 0 \land k \geq x \land x \leq 8-k \land 3k-12 \leq x \land 0 \leq 3k-12]\tag{5}\\
\Longleftrightarrow~& \exists x [0 \leq x \leq k \land 3k-12 \leq x \leq 8-k \land 3k-12<0] \\
&\lor \exists x[0 \leq x \leq k \land 3k-12 \leq x \leq 8-k \land 0 \leq 3k-12]\\
\Longleftrightarrow~& (0 \leq k \land 3k-12 \leq 8-k \land 3k-12<0) \\
&\lor (0 \leq k \land 3k-12 \leq 8-k \land 0 \leq 3k-12)\tag{6}\\
\Longleftrightarrow~& (0 \leq k \land k \leq 5 \land k < 4) \lor (0 \leq k \land k \leq 5 \land 4 \leq k)\\
\Longleftrightarrow~& 0 \leq k < 4 \lor 4 \leq k \leq 5\\
\Longleftrightarrow~& 0 \leq k \leq 5
\end{align*}

したがって，最大値\(5\)，最小値\(0\)．

\((1)\)は式の主張そのままなのですが，慣れないとこの言い換えが一番難しいかも知れません．この記事と同じ考え方です．
\((2)\)は存在記号の処理
\((3)\)は恒真条件\(3k-12<0 \lor 0 \leq 3k-12\)の追加
\((4)\)は分配法則
\((5)\)は存在記号の分配
\((6)\)はこちらの記事

…と，この解法はもはや完全に趣味ですね＾＾；大人しく教科書と同じく線型計画法で解いた方が明快でスマートだと思います．しかし，この解法のおもしろポイントは絵に頼らない（数直線はイメージしますが…）で論理を’計算’する感覚で機械的に答えにたどりつく，という点です（以前紹介した軌跡の問題と同じ）．視覚的に解く以外にも，こういった論理だけでゴリゴリ攻める姿勢も身に付けておいても決して無駄にはならないと思います．

ちなみに教科書の解法（線型計画法）は\((\ast)\)の段階で視覚化を考えた，と考えられます．ですからいずれの解法にしても\((1)\)の言い換えは本来教科書レベルであっても必要なものだと思います．例によって「解ければいいや」で覚えて済ましがちですけどね．

（高校生へ注意）この記事を読む際は，教科書の定積分の定義は忘れて読んで下さい．一旦無の状態に戻るのが理解のポイントです．

私たちは四角形の面積なら求められます．タテ\(\times\)ヨコ．さらにここから，三角形の面積やら台形の面積やらをも求められることになります．では，下のような曲線を含む図形Aの面積はどうやって求めればいいのでしょうか．というか，何を指して曲線を含む図形Aの「面積」とすればいいのでしょうか？

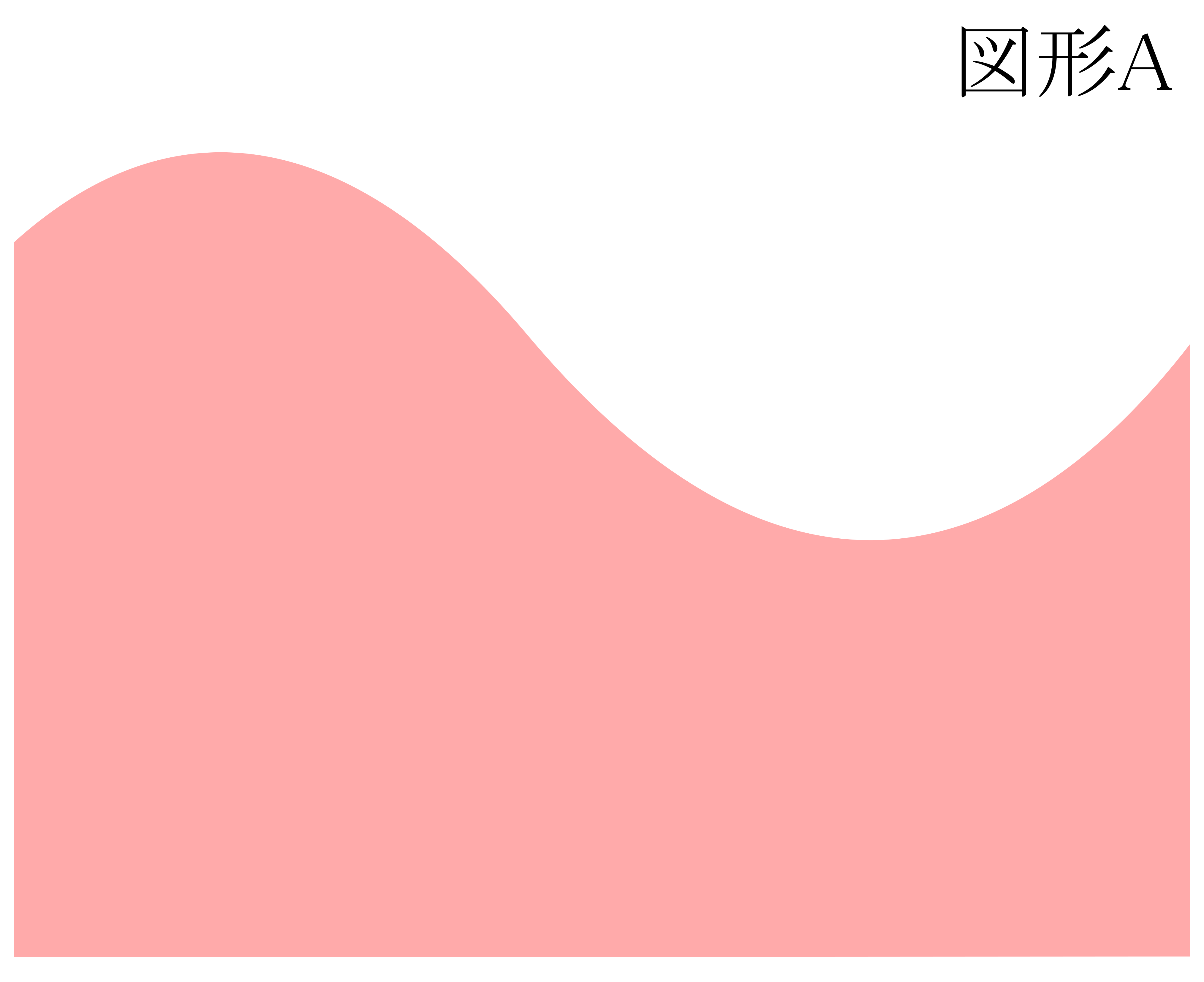
下図のような\(x\)軸，\(y=f(x)\)，\(x=a\)，\(x=b\)状況を仮定した上で，次のように考えてみます：

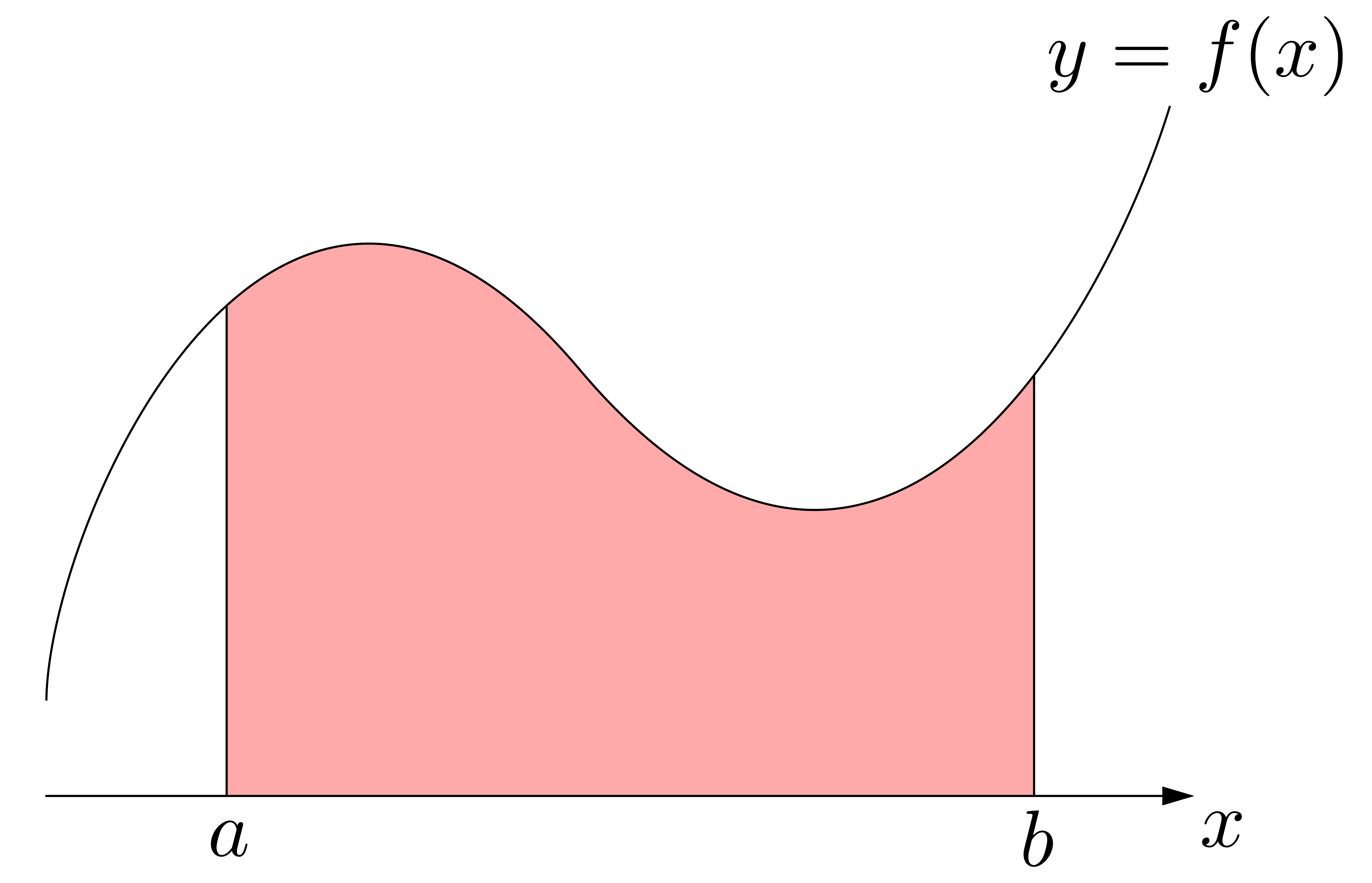
まず，図形を分割します．何個に分割してもいいのですが，ここでは\(n\)個に分割（等分でなくともよい）することにします．\[a=x_0<x_1<x_2<x_3<\cdots<x_{n-1}<x_{n}=b\]という分割です．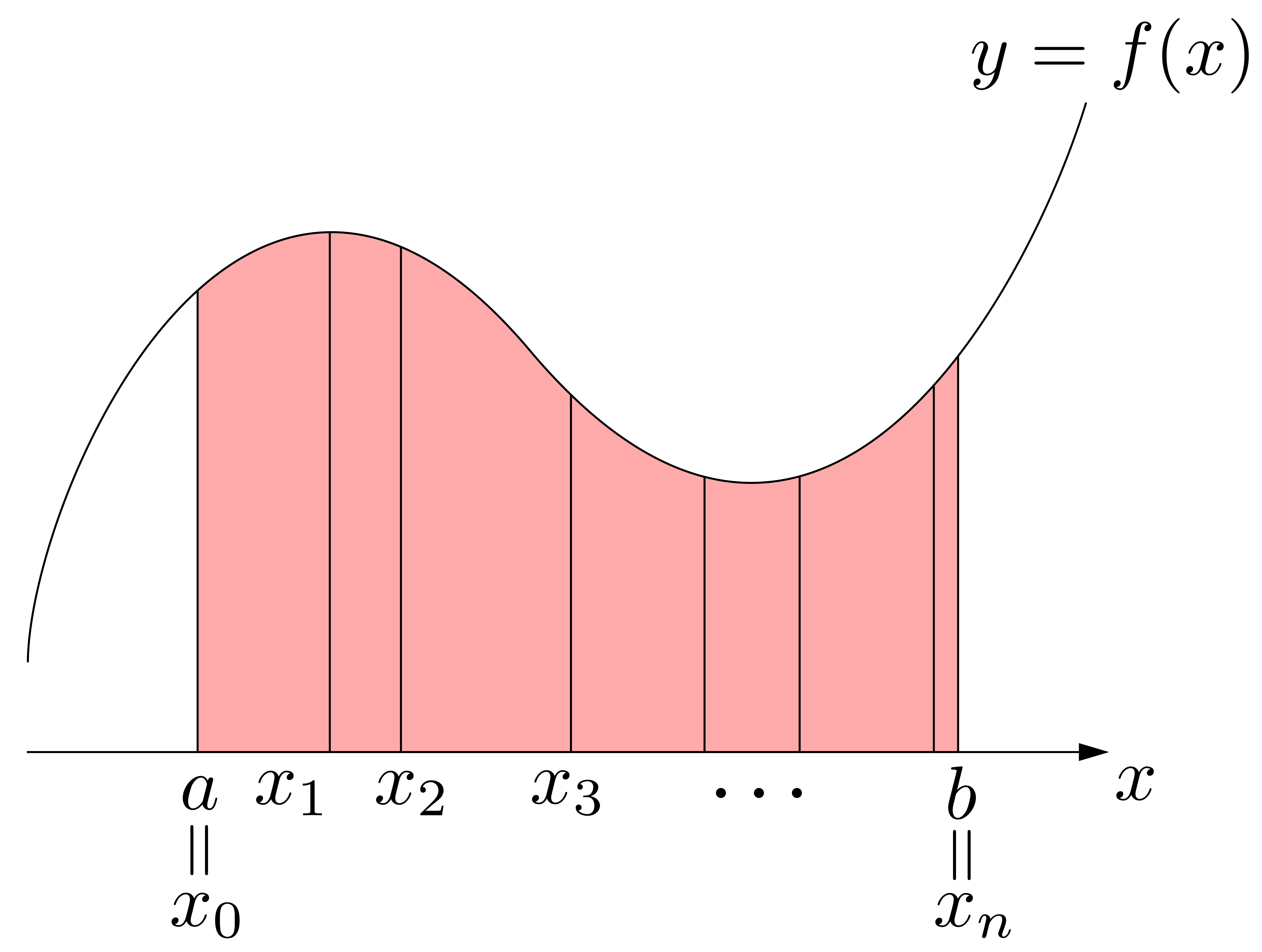

次に，これら\(n\)個の図形を，長方形に近似します．区間\([x_{i-1},~x_{i}]\)において「高さ」をとる\(x\)を\(\xi_i\)とします．区間\([x_{i-1},~x_{i}]\)上のどの点\(x\)を\(\xi_i\)とするかは任意です（ちなみに\(\xi\)はギリシャ文字で「グザイ」「クシー」などと読みます）．

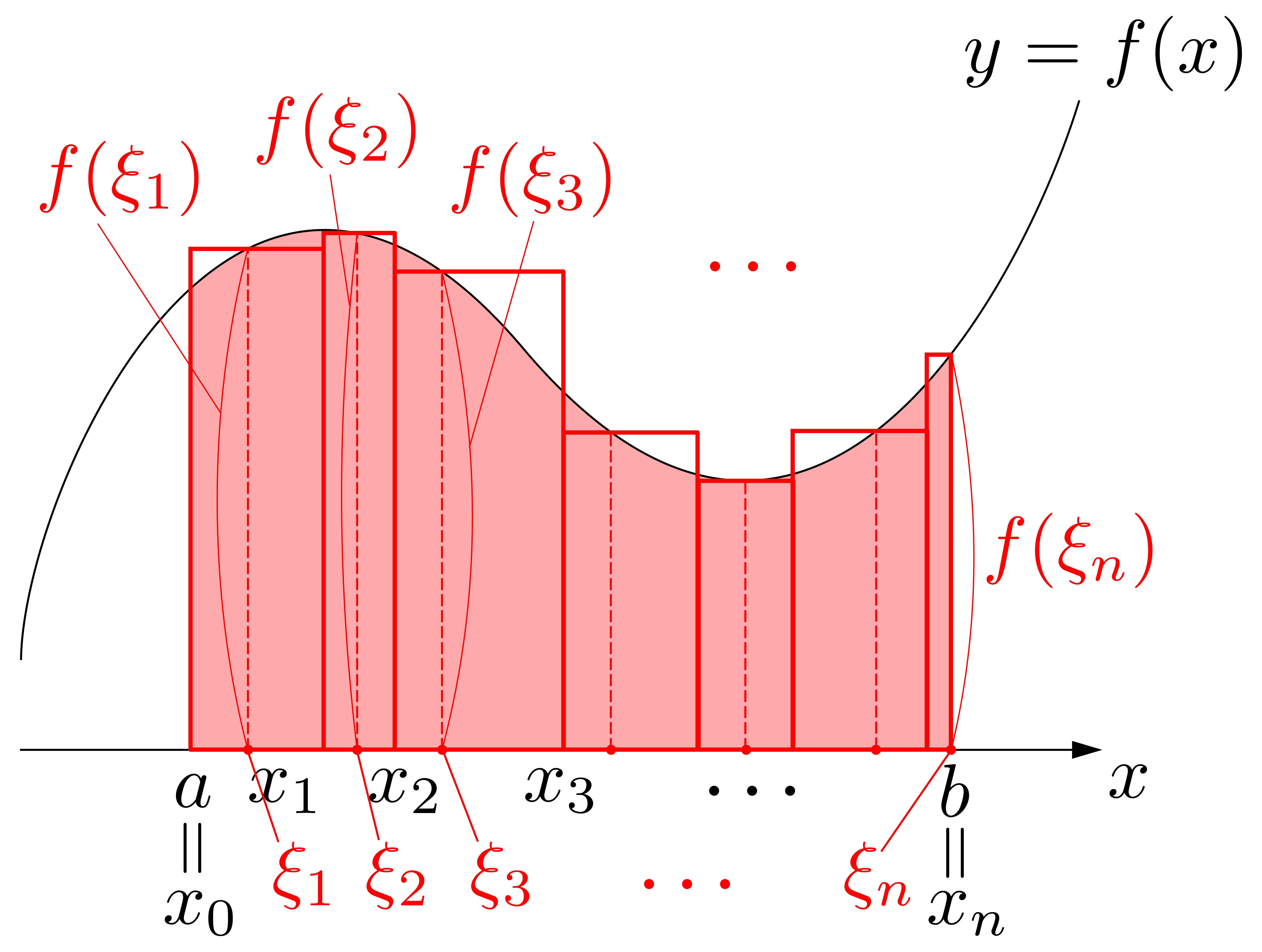
これらの長方形の面積を求めます．例えば左から\(i\)番目の長方形の面積なら，横幅は\(x_{i}-x_{i-1}\)です．高さは\(f(\xi_i)\)です．したがって左から\(i\)番目の長方形の面積は
\[f(\xi_i)(x_{i+1}-x_i)\]
と書けます．さらに，\(x_{i+1}-x_i=\Delta x_i\)とおけば，
\[f(\xi_i)\Delta x_i\]
と書けます．これを\(n\)個寄せ集めるのですから，敷き詰めた長方形の面積の和は
\[\sum^{n}_{i=0}f(\xi_i)\Delta x_i\]
と表されることになります．これをリーマン和と呼びます．

この「リーマン和」をもってして図形Aの「面積」とするのはどうでしょうか？…それはちょっとマズイ気がします．なぜなら，図形Aとリーマン和とではスキマ（誤差）が大きすぎますから（下図参照）．

どうすればスキマ（誤差）は小さくなるでしょうか？各長方形の幅を小さくすれば，細長い長方形になって，スキマは小さくなります．当然，スキマは小さければ小さいほど，今私たちにとって欲しいものが正確に求まりそうな気がします．各長方形の幅を小さくするには，\(n\)を大きく，すなわち分割の数を大きくしてやればいいでしょう．

式で表すと，
\[\lim_{n\rightarrow \infty}\sum^{n}_{i=0}f(\xi_i)\Delta x_i\]
これなら，図形の「面積」と呼んでも差し支えなさそうです．そこで，この極限値を図形Ａの「面積」と定義し，「定積分」と名付け，記号\[\int^b_a f(x)dx\]で表すことにします．

\(:=\)は「左辺を右辺で定義する」という意味です．

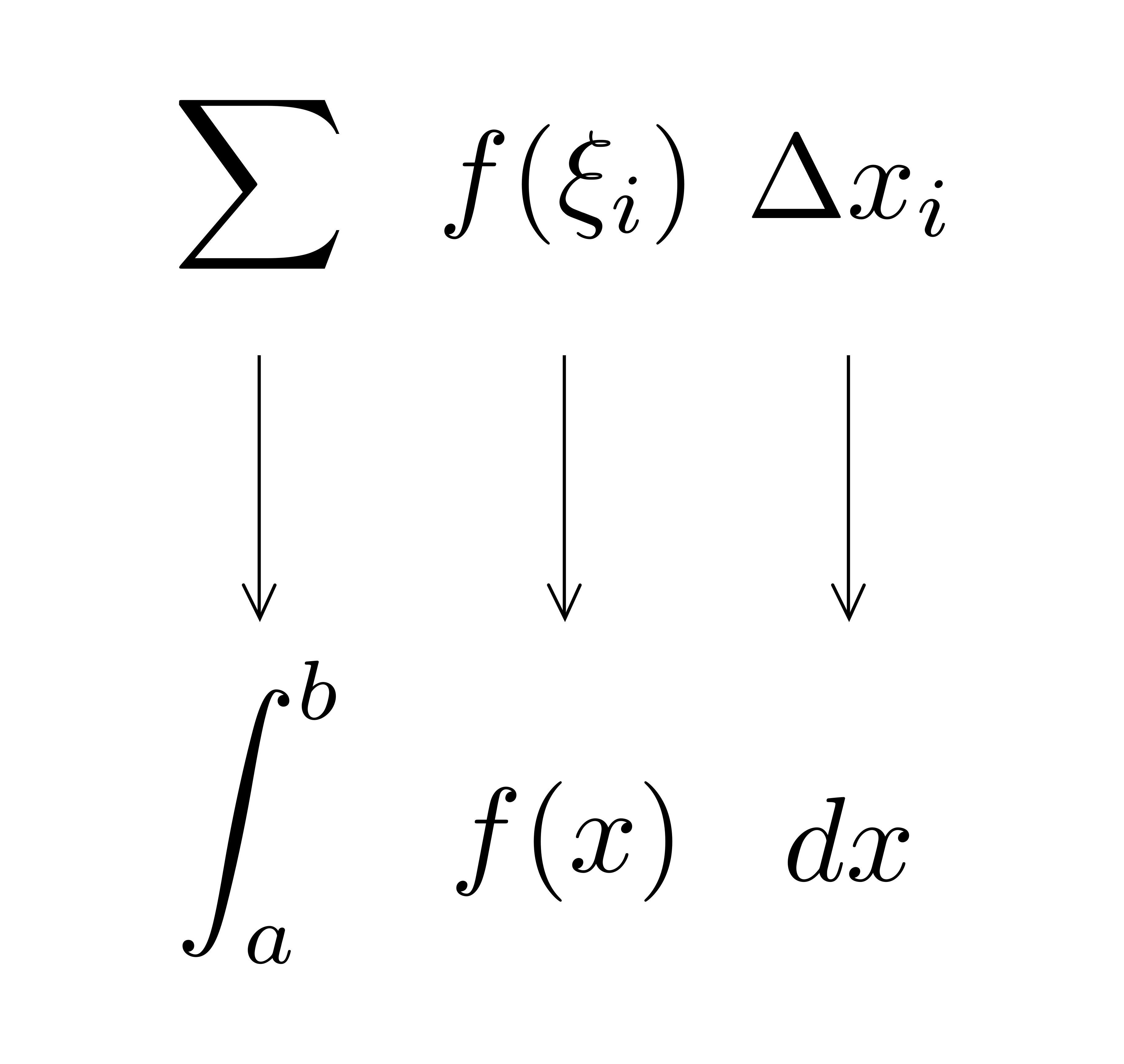以上を見ると，\(\displaystyle \int^b_a f(x)dx\)の\(\displaystyle \int\)や\(dx\)の「イメージ」が見えてきます．右図に示すように，\(\displaystyle \sum\)が\(\displaystyle \int\)に，\(\Delta x_i\)が\(dx\)と対応しているわけです．

ここで，\(\displaystyle \sum\ f(\xi_i)\Delta x_i\)の意味を思い出しましょう．\(f(\xi_i)\)が「タテ」，\(\Delta x_i\)が「ヨコ」を表すのでしたから，\(f(\xi_i)\times\Delta x_i\)は「長方形の面積」を意味し，その長方形の面積\(f(\xi_i)\Delta x_i\)を\(\displaystyle \sum\)する（足し加える），という意味でした．

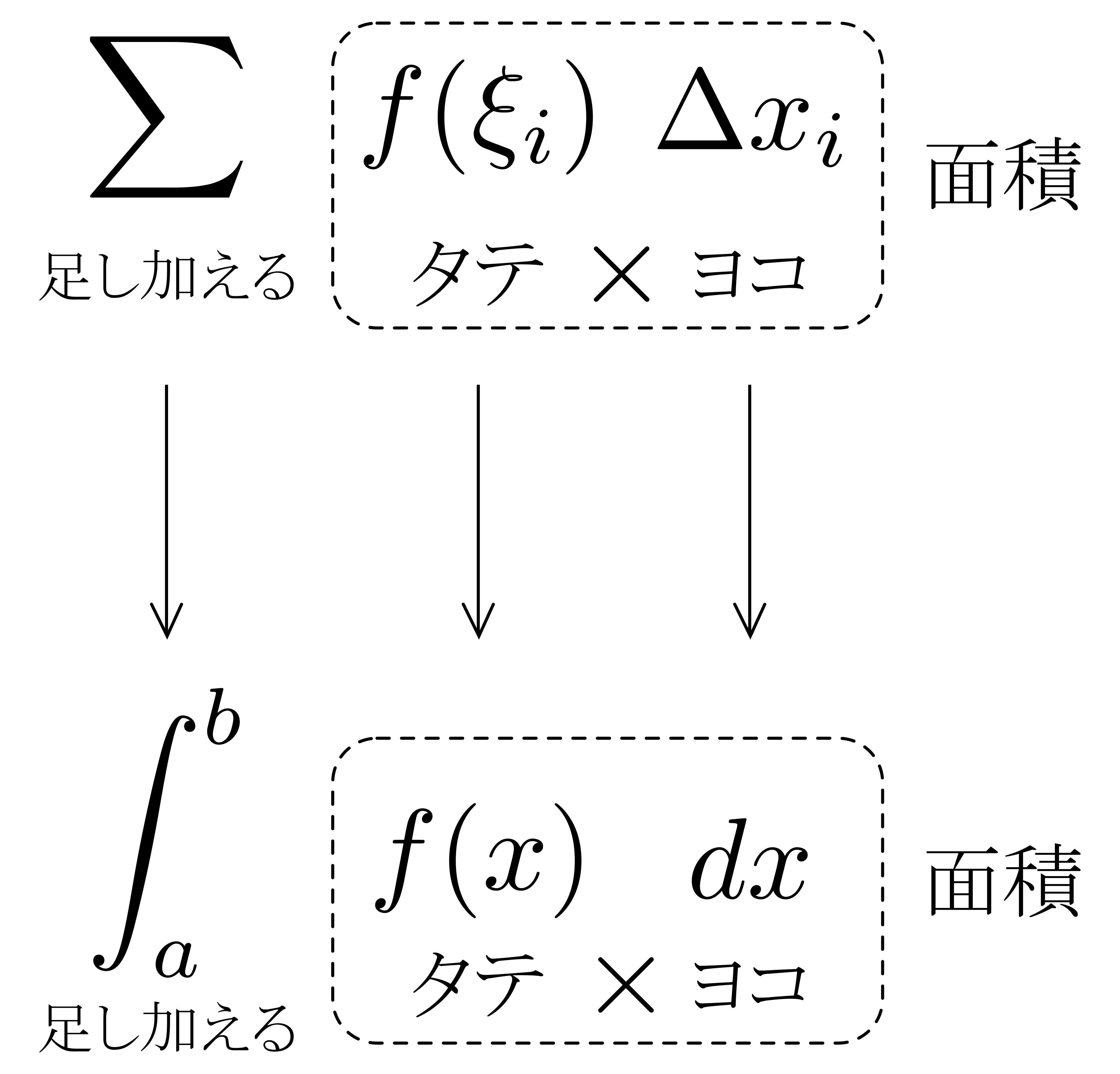以上を踏まえて\(\displaystyle \int^b_a f(x)dx\)を眺めると，これは「微小面積\(f(x)\times dx\)を\(\displaystyle \int\)したもの（連続的に足し加えたもの）」と読み取れることが分かります！

定積分を「リーマン和の極限」とみなす捉え方は，とても自然で，記号の導入も全く違和感がありません．さらに，右図に示した記号の解釈は，定積分の問題を扱う上で極めて重要な解釈になります．

次回はこの定積分の定義に従って図形の面積を計算してみます．すると，大きな問題に直面します…．

高校教科書では，定積分を次のように定義しています．

そして，数学Ⅱまたは数学Ⅲで積分を既習の人はこの定積分を計算することによって「面積が求まる」ということも知っていると思います．

しかし，ここでひとつ疑問．なぜ定積分で面積が求まるのでしょうか？定積分の定義は上に示したようにあくまで「原始関数の差を『定積分』と呼ぶことにしましょう」と言っているに過ぎず，「面積」云々には一切触れていません．つまり（定積分の「定義」から）「面積が求まる」ということが「定理」として得られるはずですが，その理由はどこにあるのでしょうか？その辺を理解しないままにただただ計算している人も多いのではないでしょうか．

調べてみましょう．

今，\(y=f(x),~x\leq k,~y=0\)で示される部分の面積を\(S(k)\)と表すことにします．

すると，\(y=f(x),~x=x_1,~x=x_2,~y=0\)で囲まれる部分の面積は，\[S(x_2)-S(x_1)\]で表されることになります．

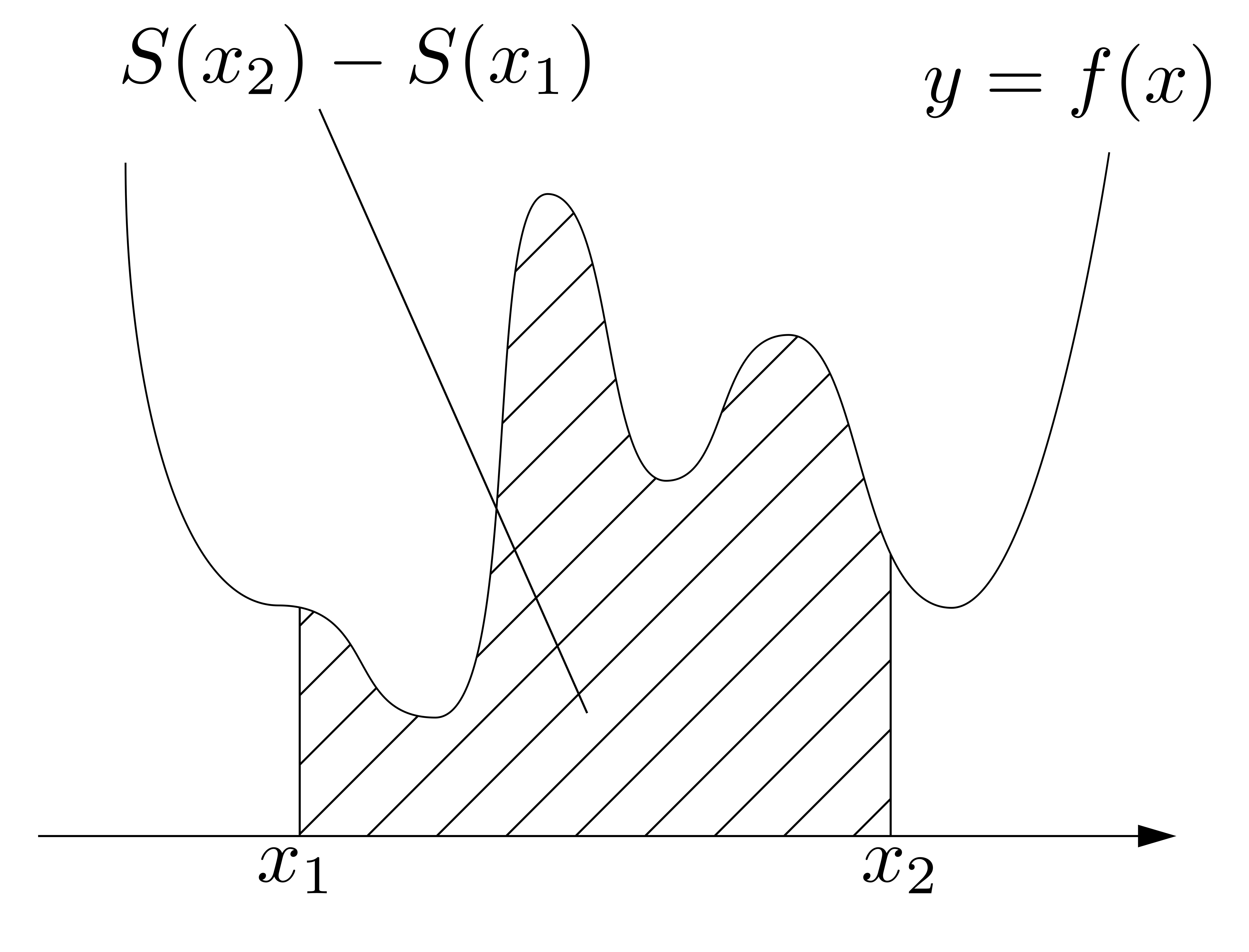
この斜線部分の面積を評価することを考えます．斜線部分の面積\(S(x_2)-S(x_1)\)は，区間\([x_1,~x_2]\)の幅\(x_2-x_1\)を「ヨコ」，区間\([x_1,~x_2]\)で一番大きい\(y\)の値\(f(x_{max})\)を「タテ」としたときの長方形の面積\((x_2-x_1)f(x_{max})\)より小さく，区間\([x_1,~x_2]\)の幅\(x_2-x_1\)を「ヨコ」，区間\([x_1,~x_2]\)で一番小さい\(y\)の値\(f(x_{min})\)を「タテ」としたときの長方形の面積\((x_2-x_1)f(x_{min})\)よりも大きいと言えます（下図参照．一番大きい，または小さい\(y\)の値を取るときの\(x\)をそれぞれ\(x_{max},~x_{min}\)とおきました）．

したがって，以下の不等式が成り立ちます．
\[(x_2-x_1)f(x_{min})\leq S(x_2)-S(x_1)\leq (x_2-x_1)f(x_{max})\]
さらに，辺々を\(x_2-x_1\)で割ることで，
\[f(x_{min})\leq \frac{S(x_2)-S(x_1)}{x_2-x_1}\leq f(x_{max})\]
が得られます．

ここで，\(x_2\)を\(x_1\)に近づけてみます．すなわち，
\[\lim_{x_2\rightarrow x_1}f(x_{min})\leq \lim_{x_2\rightarrow x_1}\frac{S(x_2)-S(x_1)}{x_2-x_1}\leq \lim_{x_2\rightarrow x_1}f(x_{max})\]
まず中辺ですが，これは導関数の定義から\[S'(x_1)\]と書けます．

次に左辺と右辺について．\(x_2\)を\(x_1\)に近づけるというのは，区間\([x_1,x_2]\)の幅を縮めるということですから，図から\(f(x_{max}),~f(x_{min})\)はどちらも\(f(x_1)\)に近づくことが分かります（下図参照）．

すなわち，
\[\lim_{x_2\rightarrow x_1}f(x_{max})=\lim_{x_2\rightarrow x_1}f(x_{max})=f(x_1)\]

したがって，はさみうちの原理から
\[S'(x_1)=f(x_1)\]
が得られますが，この式は
\[S(x_1)=\text{\(f(x_1)\)の原始関数}\]
であることを示しています．添え字がちょっとうるさいので\(x_1\)を\(x\)に置き換えておきます．
\[S(x)=\text{\(f(x)\)の原始関数}\]
準備は整いました．定積分の定義\(\displaystyle \int^b_a f(x)dx=F(b)-F(a)\)を変形してみます．
\[
\begin{align}
\int^b_a f(x)dx=&F(b)-F(a)\\
=&\text{\(f(x)\)の原始関数}|_{x=b}-\text{\(f(x)\)の原始関数}|_{x=a}\tag{1}\\
=&S(x)|_{x=b}-S(x)|_{x=a}\tag{2}\\
=&S(b)-S(a)
\end{align}
\]
\((1)\)は定義の仮定：「\(F(x)=\text{\(f(x)\)の原始関数}\)」から，
\((2)\)は先に導いた式：「\(S(x)=\text{\(f(x)\)の原始関数}\)」によるものです．

結局，
\[\int^b_a f(x)dx=S(b)-S(a)\]
が得られますが，\(S(b)-S(a)\)は\(y=f(x),~x=a,~x=b,~y=0\)で囲まれた面積を表しますから，定積分すなわち原始関数の差は確かに面積を表すことが確認でしました．

以上により定積分で面積が求められることが一応納得はできました．しかしながら，この「納得」は上でみたように複雑で，お世辞にも「直観的」とは言えません．一般に求積問題は図形が絡むので視覚情報から解法に繋げていくことが多いのですが，その視覚情報を数式に落とし込むにはある種の「直観的」な理解が必要になってきます．教科書の定義のままでは直観的な理解が伴わないゆえに求積問題等ではうまく発想・立式ができず，ほとんど使い物になりません．数学が得意な人，これから得意にしたい人，あるいは将来的に数学を使う学部学科に進みたい人は違う角度で定積分というものを捉える（理解する）べきです．

次回，「定積分」を教科書とは違う角度から（リーマン和の極限として）再定義し，今度は逆に「定積分が原始関数の差である」ことを定理として導いてみようと思います．すなわち，教科書が「定積分とは原始関数の差である（定義）→定積分は面積である（定理）」という流れであったのに対し，逆に「定積分はリーマン和の極限（＝面積）である（定義）→定積分は原始関数の差である（定理）」という流れで定積分というものを捉え直します．この考え方自体がとりもなおさず受験数学における求積問題の肝にもなります．

点と直線の距離の公式を証明してみましょう．

直線\(l:ax+by+c=0\)と，この直線上にない点を\(\mathrm{P}(x_0,~y_0)\)，そして下図に示す直線\(l\)上の点を\(\mathrm{A}(p,~q)\)とします．

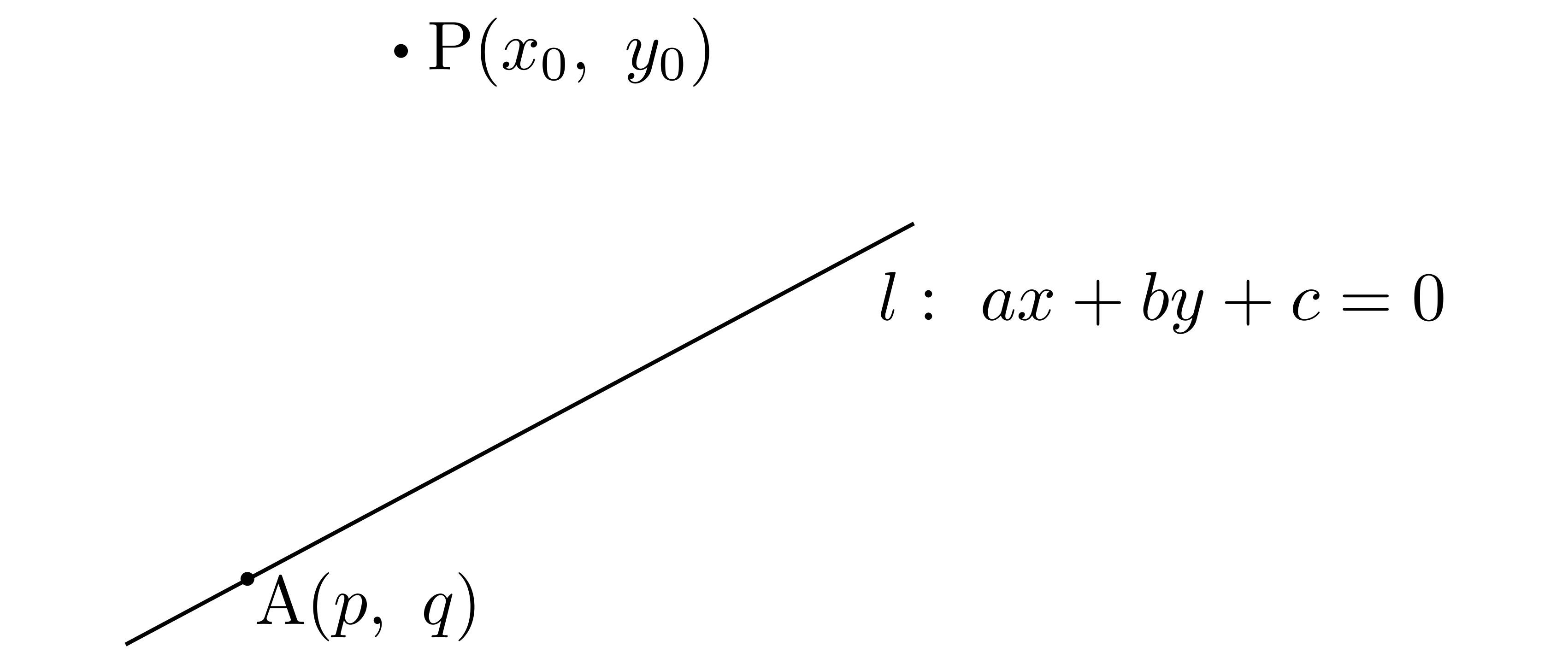
まず\(l\)の法線ベクトルを求め，図示します．法線ベクトルは\(x\)と\(y\)との係数から\((a,~b)\)でしたね（なぜ？）．また，\(\overrightarrow{\mathrm{AP}}\)を図示しておきます．（下図では\((a,~b)\)を列ベクトルで表記しています．）

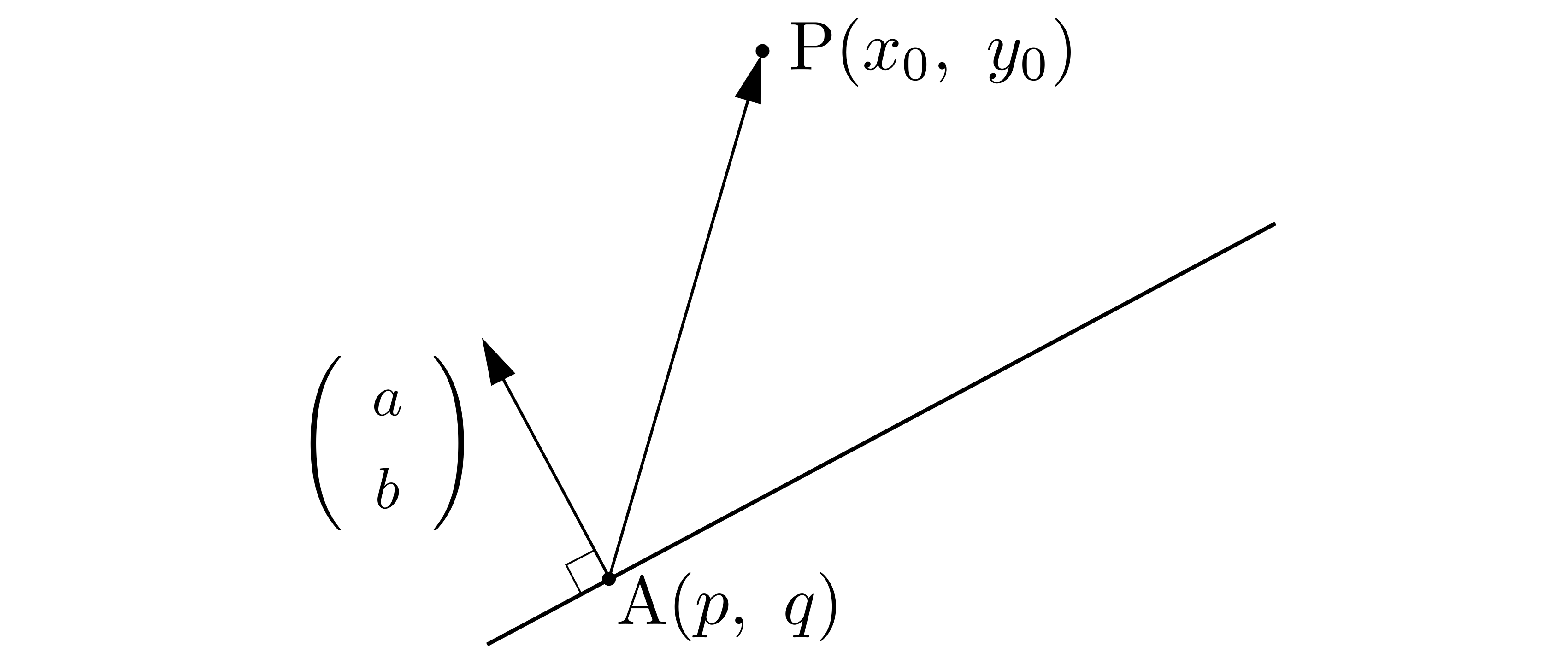
求めたいものも図示しておきましょう．それは，

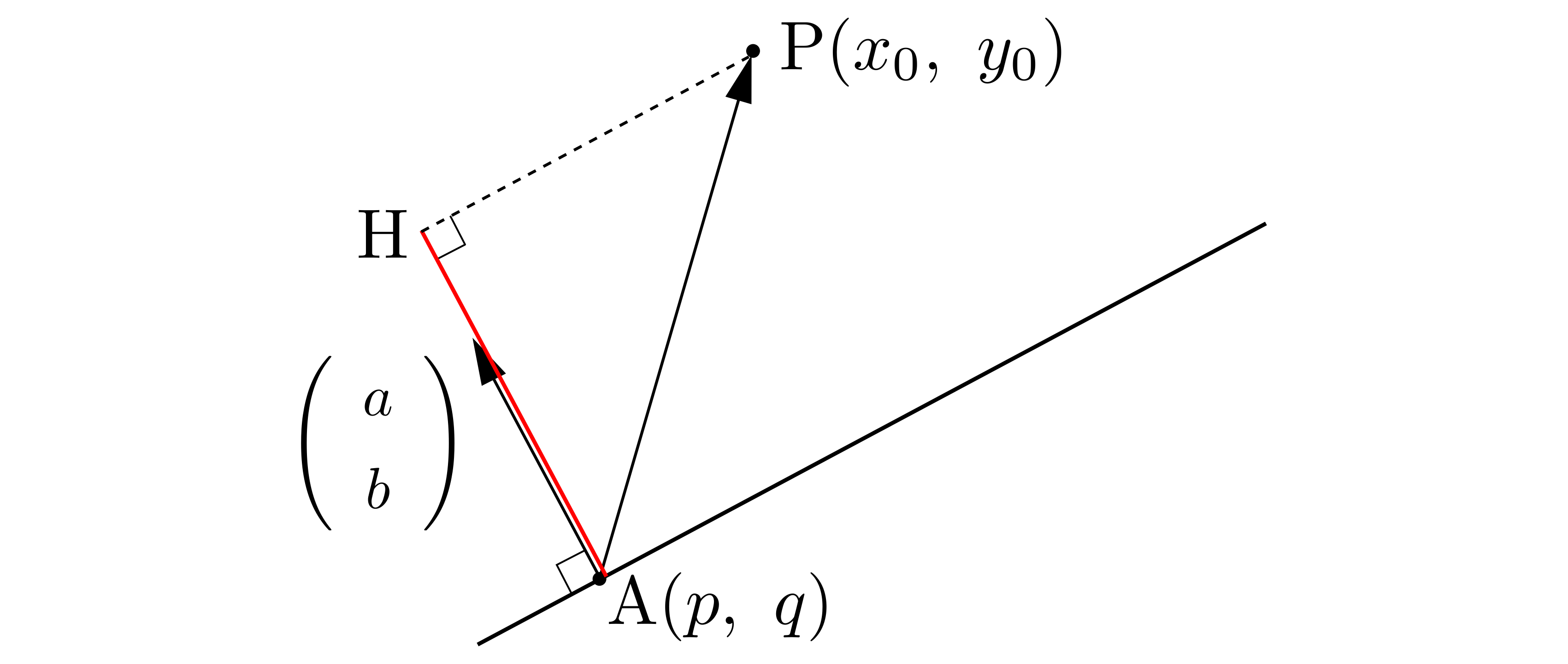
上図の赤い線分\(\mathrm{AH}(=|\overrightarrow{\mathrm{AH}}|)\)ですね．

気づいたでしょうか？これはほかならぬ正射影ベクトル（の大きさ）です．ですから結局，「点と直線の距離は，正射影ベクトルを求めて，その大きさを求めればよい」と分かります．

ここで正射影ベクトルの公式の出番です！

正射影ベクトルを求めるために，ベクトル\((a,~b)\)を正規化（大きさを１にすること）しておきましょう：
\[\frac{1}{\sqrt{a^2+b^2}}
\left(\begin{array}{c}
a \\
b \\
\end{array}\right)
\]
このベクトルを\(\overrightarrow{n}\)とおきます．すると，正射影ベクトルの公式から，\(\overrightarrow{\mathrm{AH}}\)は\[(\overrightarrow{\mathrm{AP}}\cdot\overrightarrow{n})\overrightarrow{n}\]と書けますね．\[\overrightarrow{\mathrm{AP}}=\left(\begin{array}{c} x_0\\ y_0\end{array}\right)-\left(\begin{array}{c} p\\ q\end{array}\right)=\left(\begin{array}{c} x_0-p\\ y_0-q\end{array}\right)
\]
ですから，計算すると
\[
\begin{align*}
&\overrightarrow{\mathrm{AH}}=(\overrightarrow{\mathrm{AP}}\cdot\overrightarrow{n})\overrightarrow{n}\\
=&\left\{\left(\begin{array}{c} x_0-p\\ y_0-q\end{array}\right)\cdot\frac{1}{\sqrt{a^2+b^2}}
\left(\begin{array}{c}
a \\
b \\
\end{array}\right)\right\}\overrightarrow{n}\\
=&\frac{a(x_0-p)+b(y_0-q)}{\sqrt{a^2+b^2}}\overrightarrow{n}
\end{align*}
\]
\(\mathrm{AH}=|\overrightarrow{\mathrm{AH}}|\)ですから，\(\left| \overrightarrow{n}\right|=1\)であることに注意して，
\[
\begin{align*}
\mathrm{AH}=&|\overrightarrow{\mathrm{AH}}|\\
=&\left|\frac{a(x_0-p)+b(y_0-q)}{\sqrt{a^2+b^2}}\overrightarrow{n}\right|\\
=&\frac{|ax_0+by_0-ap-bq|}{\sqrt{a^2+b^2}}|\overrightarrow{n}|\\
=&\frac{|ax_0+by_0-ap-bq|}{\sqrt{a^2+b^2}}
\end{align*}
\]
ここで，\((p,~q)\)は直線\(l\)上の点でしたから，\[ap+bq+c=0\quad \text{すなわち}\quad c=-ap-bq\]が成り立ちます．したがって，上の式は結局
\[\mathrm{AH}=\frac{|ax_0+by_0+c|}{\sqrt{a^2+b^2}}\]となります．

この証明のいいところは，まず簡潔で記述量（計算量）が少ない（＝かっこいい）という点，それにこの公式の三次元バージョンとでもいいますか「点の平面の距離の公式」を導出する際もまったく同じように応用できるという点です．他にも，数学検定１級１次の問題でこのアイデアが使える問題がありました．いずれ紹介したいと思います．

また，この証明を通して「正射影ベクトルの公式」の使いどころも感じて貰えたかと思います．

今回はとりあえずここまでにして，「点と平面の距離の公式」も後ほど記事にしてみたいと思います．