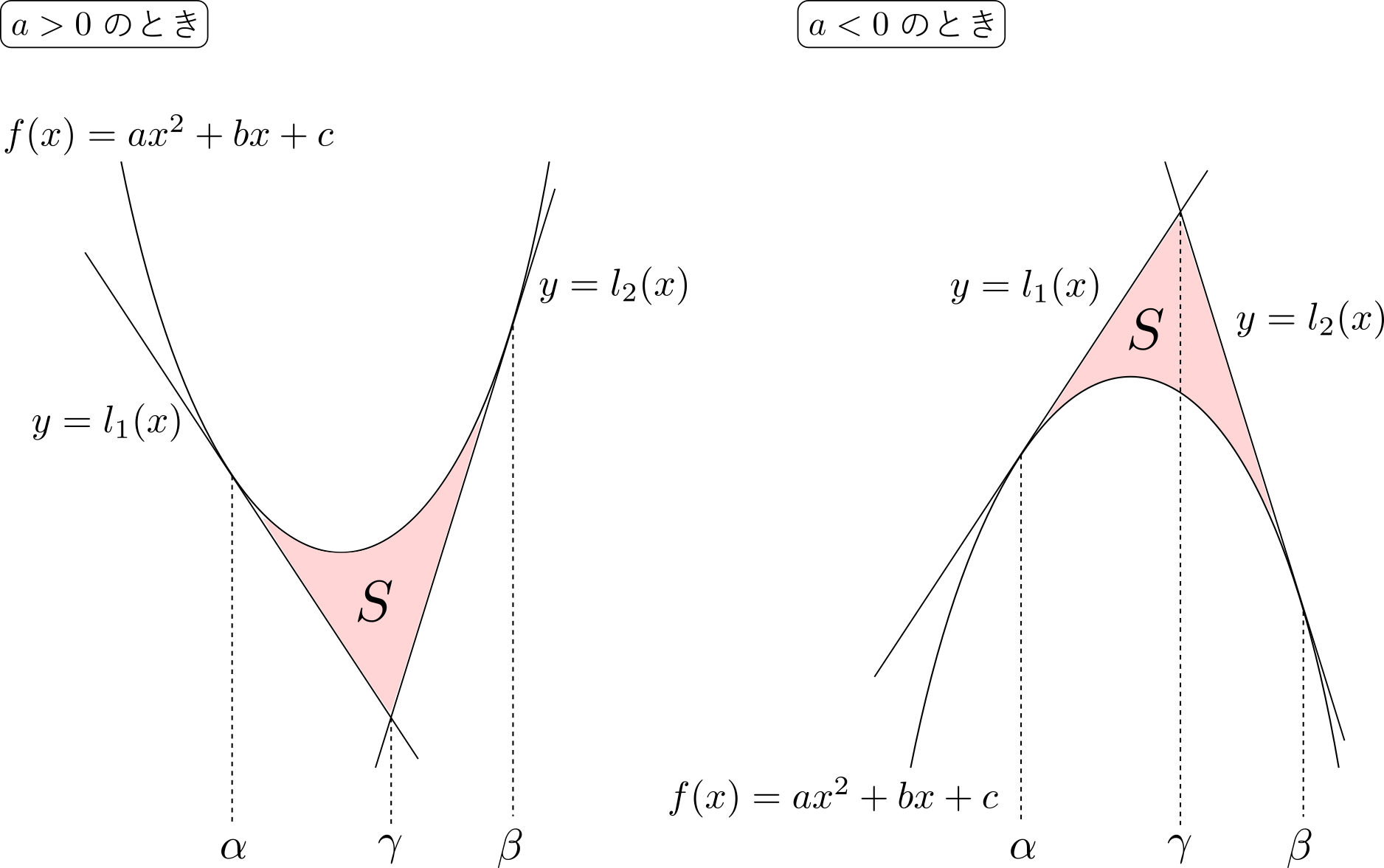
上の曲線と直線で囲まれる部分の面積\(S\)は,いずれの場合も\[S = \frac{|a|(\beta-\alpha)^3}{12}\]で表される.
証明
\(a>0\)のとき.まず\(\gamma\)を求める.そのためには,\(l_{1}(x),~l_{2}(x)\)を求めて連立すればよい.
\(l_{1}(x)\)を求めるために,\(f(x)-l_{1}(x)\)がどんな関数になるかを考える.これは,
-
-
- \(2\)次式で,
- 次数が一番大きい項の係数は\(a\)で,
- \(x=\alpha\)で接している,すなわち\(f(x)-l_{1}(x)=0\)を解いて得られる\(2\)つの解が\(\alpha,\alpha\)である
-
ことに着目すると,\[f(x)-l_{1}(x) = a(x-\alpha)^2\]とかける.したがって\(l_{1}(x) = f(x) – a(x-\alpha)^2\).同様に考え,\(l_{2}(x) =f(x)- a(x-\beta)^2\).この\(2\)式から,
\begin{align*}
&f(x) – a(x-\alpha)^2 = f(x)- a(x-\beta)^2 \\
\Longleftrightarrow ~& (x-\alpha)^2 = (x-\beta)^2\\
\Longleftrightarrow ~& -2\alpha x +\alpha^2 = -2\beta x +\beta^2\\
\Longleftrightarrow ~& 2(\beta – \alpha) x = \beta^2 – \alpha^2\\
\Longleftrightarrow ~& x = \frac{\alpha + \beta}{2}\\
\end{align*}ゆえに\(\gamma = \frac{\alpha + \beta}{2}\).よって,求める面積\(S\)は,
\begin{align*}
S = \displaystyle &\int_\alpha^\gamma \{f(x)- l_{1}(x)\}dx + \int_\gamma^\beta \{f(x)- l_{2}(x)\}dx\\
=&\int_\alpha^\gamma a(x-\alpha)^2 dx + \int_\gamma^\beta a(x-\beta)^2 dx\\
=&a\left[\frac{(x-\alpha)^3}{3}\right]_\alpha^\gamma + a\left[\frac{(x-\beta)^3}{3}\right]_\gamma^\beta\\
=&\frac{a}{3}\left\{(\gamma-\alpha)^3 – (\gamma-\beta)^3\right\}\\
=&\frac{a}{3}\left\{\frac{(\beta-\alpha)^3}{8} – \frac{(\alpha-\beta)^3}{8}\right\}\\
=&\frac{a}{3\cdot 8}\left\{(\beta-\alpha)^3 + (\beta-\alpha)^3\right\}\\
=&\frac{a(\beta-\alpha)^3}{12}\\
=&\frac{|a|(\beta-\alpha)^3}{12}
\end{align*}
\(a<0\)のときも同様に計算すると,やはり\(\frac{|a|(\beta-\alpha)^3}{12}\)となる.
証明終
接線同士の交点が(接点がどのような位置であっても)結局\(\frac{\alpha+\beta}{2}\)で表されることは記憶しておくべきでしょう.
・・・ここまで数Ⅱ範囲で役立つ面積公式を6つ(1,2,3,4,5,6)紹介しましたが,いずれも結果そのものよりもその導出過程の方が重要です.後半の公式になればなるほど使用頻度が低くなるので,当然,使わないがゆえに忘れ易くなる.したがって必要なときに自分で作れるようにしておくべきでしょう.導出過程さえ理解しておけば,「ああなんかそんなのあったなあ」くらいの意識さえあればその場で作れます.なにより使用頻度の低い公式の記憶を維持しようとするのはコスパ悪すぎですから.(テスト直前に付け焼き刃的に覚えるのはいいかな?邪道だけど・・・^^;)


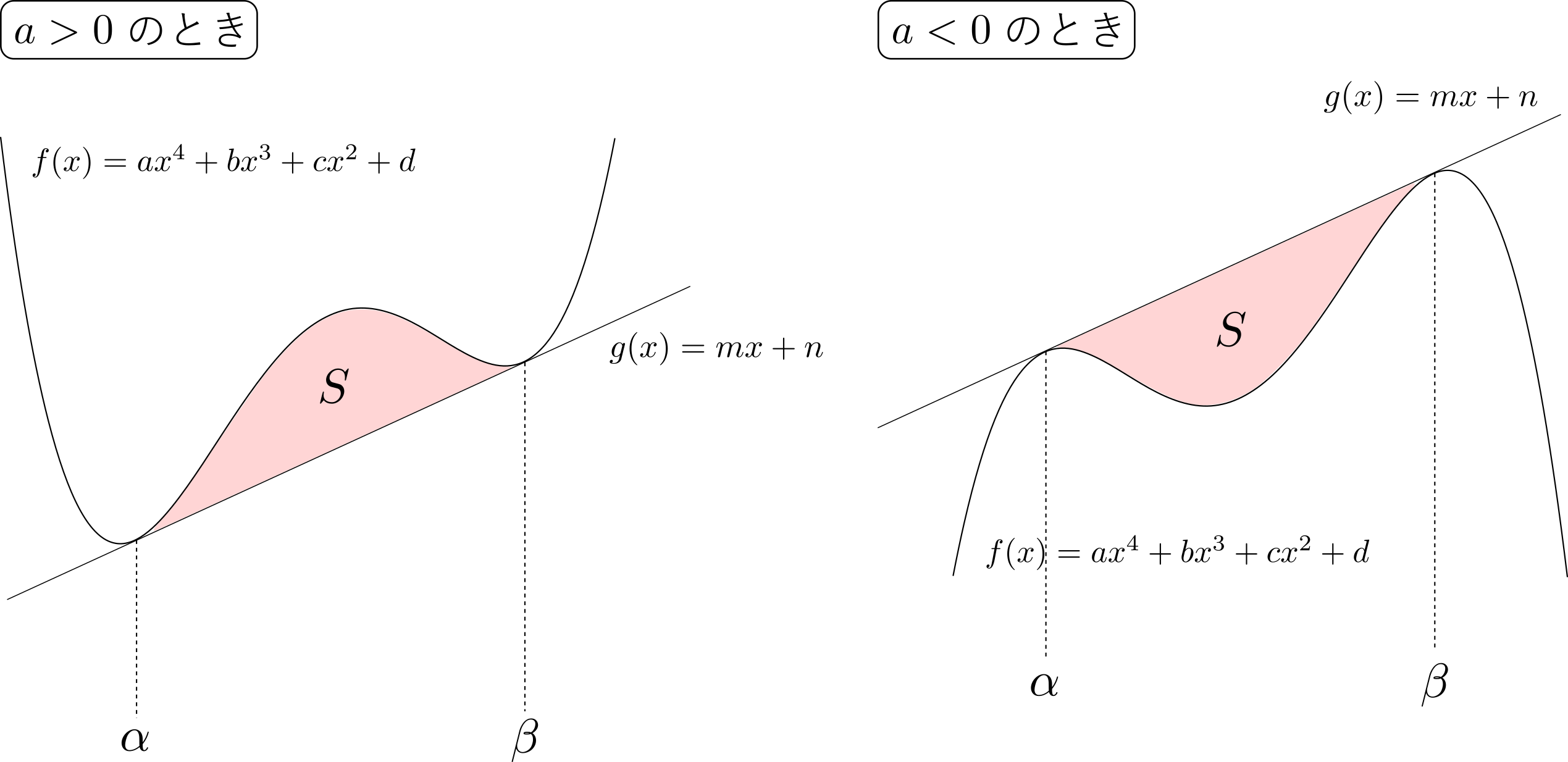
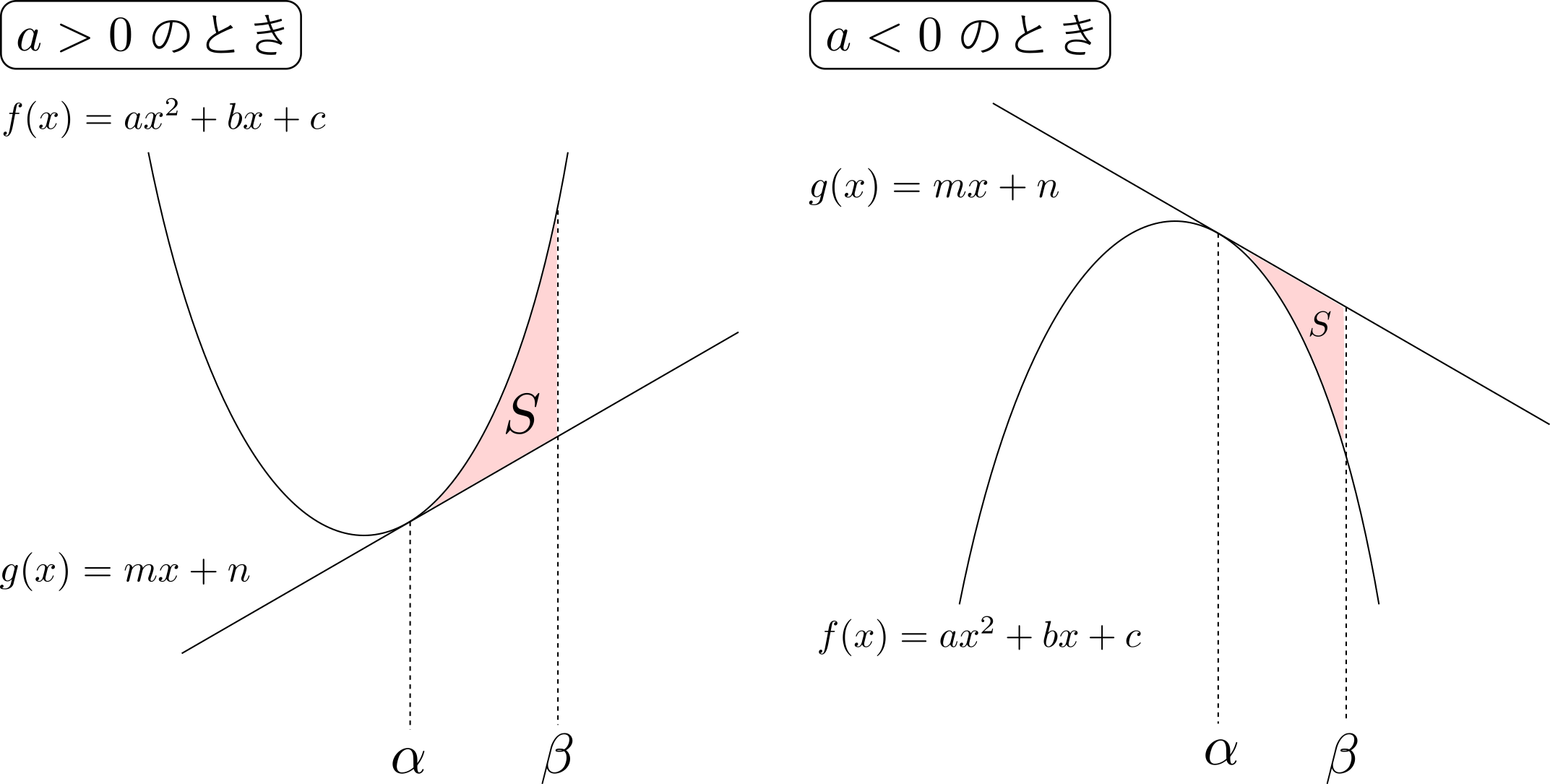
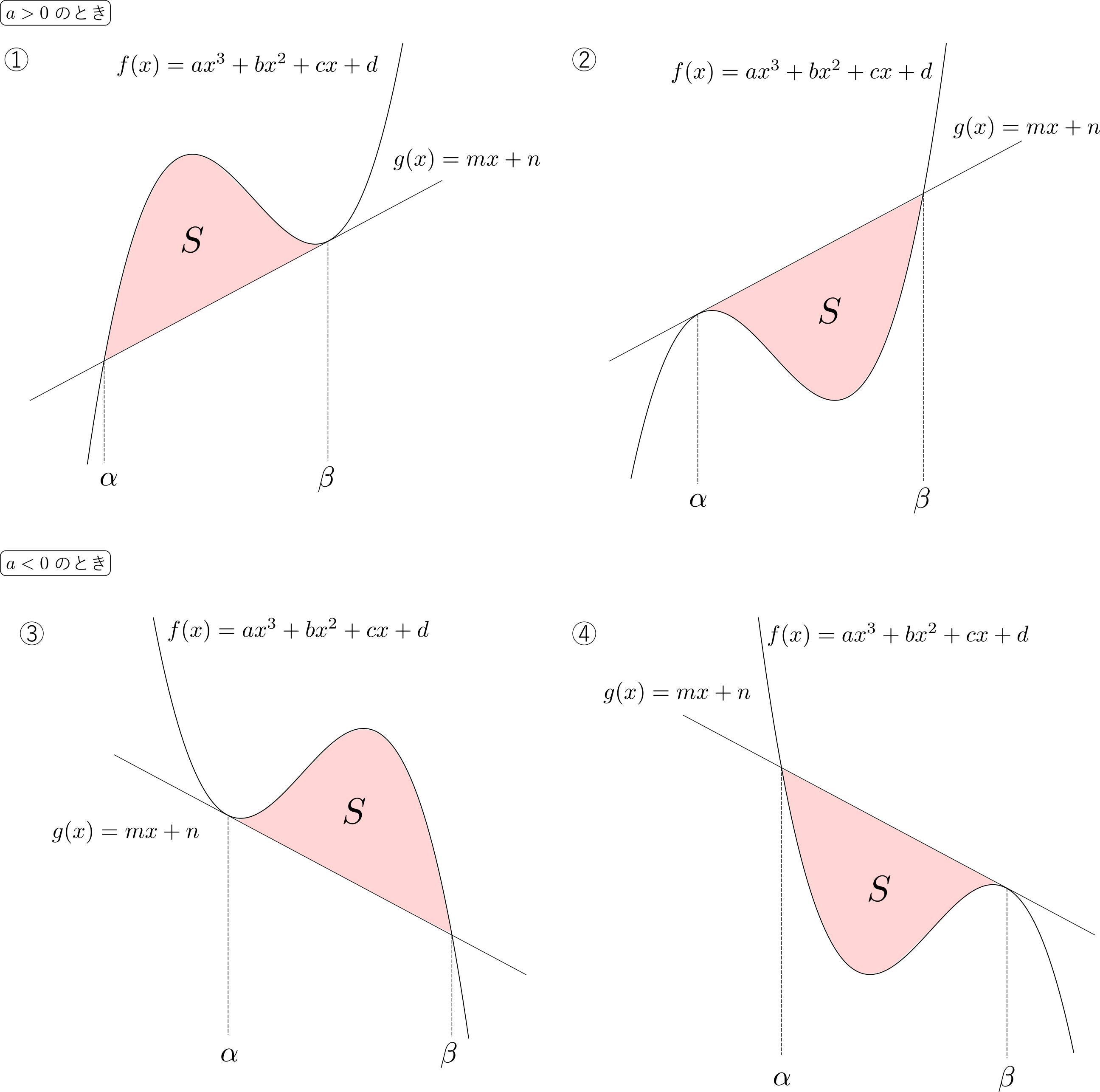 上の曲線と直線で囲まれる部分の面積\(S\)は,いずれの場合も\[S = \frac{|a|(\beta-\alpha)^4}{12}\]で表される.
上の曲線と直線で囲まれる部分の面積\(S\)は,いずれの場合も\[S = \frac{|a|(\beta-\alpha)^4}{12}\]で表される.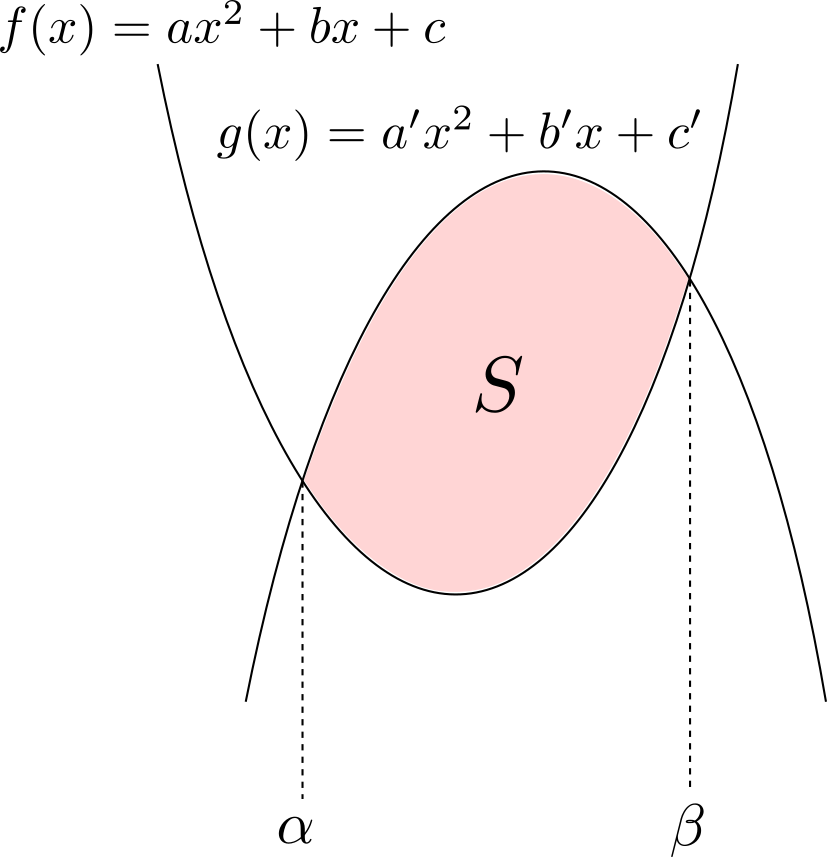

 と考えることで
と考えることで



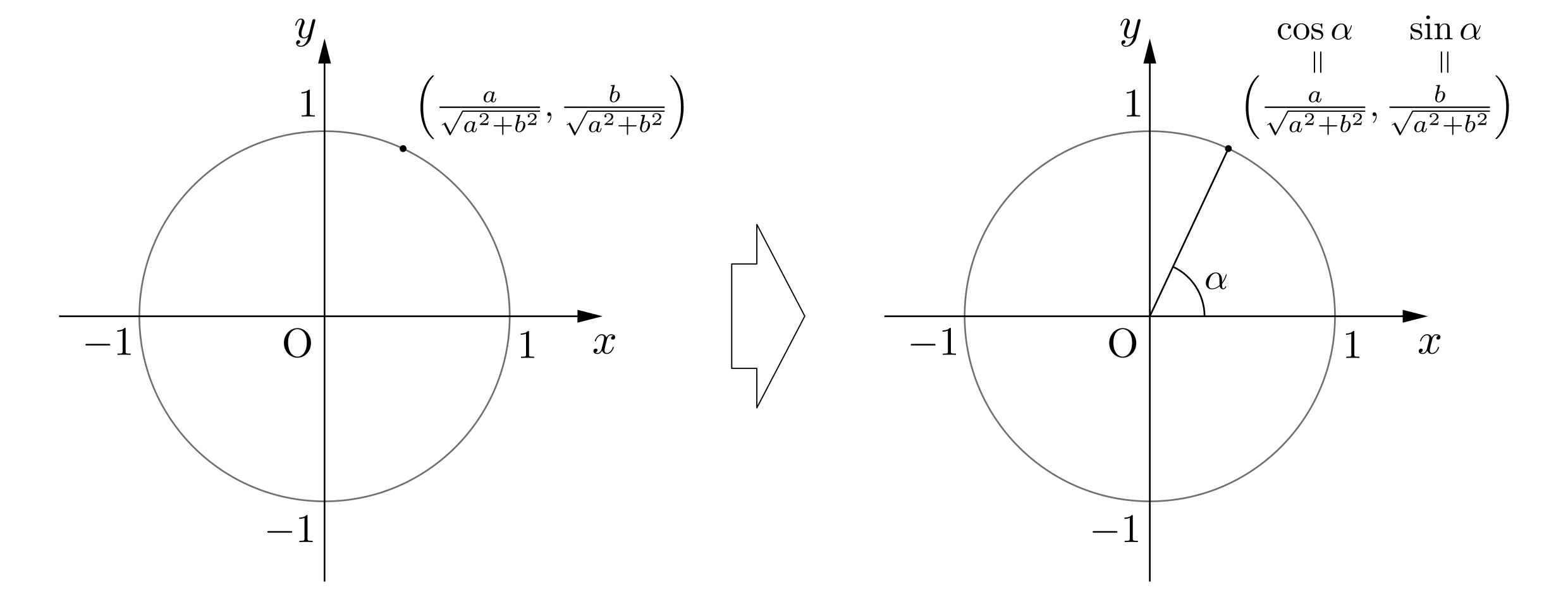 したがって
したがって