(高校生へ注意)この記事を読む際は,教科書の定積分の定義は忘れて読んで下さい.一旦無の状態に戻るのが理解のポイントです.
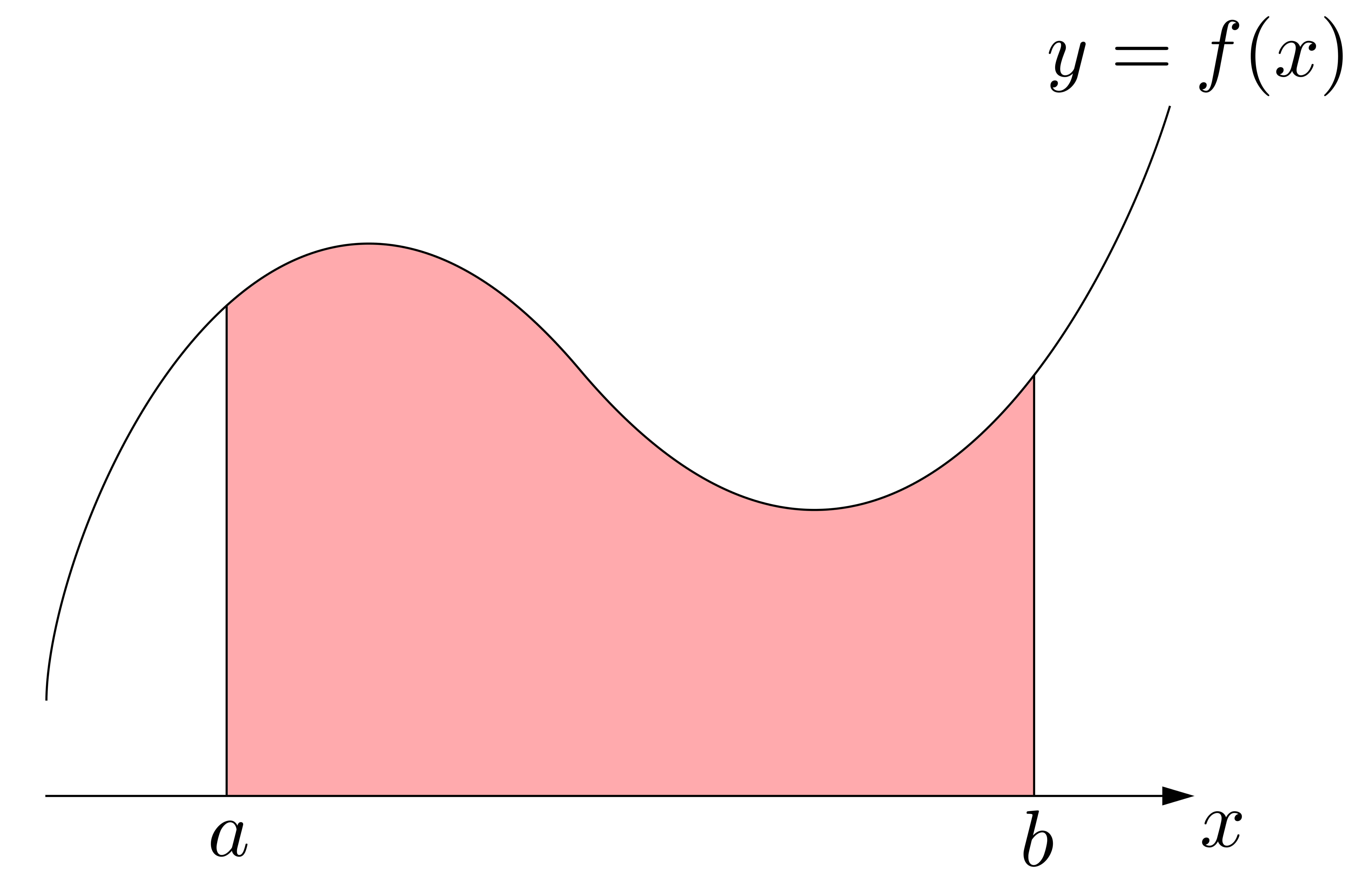
私たちは四角形の面積なら求められます.タテ\(\times\)ヨコ.さらにここから,三角形の面積やら台形の面積やらをも求められることになります.では,下のような曲線を含む図形Aの面積はどうやって求めればいいのでしょうか.というか,何を指して曲線を含む図形Aの「面積」とすればいいのでしょうか?
下図のような\(x\)軸,\(y=f(x)\),\(x=a\),\(x=b\)状況を仮定した上で,次のように考えてみます:
まず,図形を分割します.何個に分割してもいいのですが,ここでは\(n\)個に分割(等分でなくともよい)することにします.\[a=x_0<x_1<x_2<x_3<\cdots<x_{n-1}<x_{n}=b\]という分割です.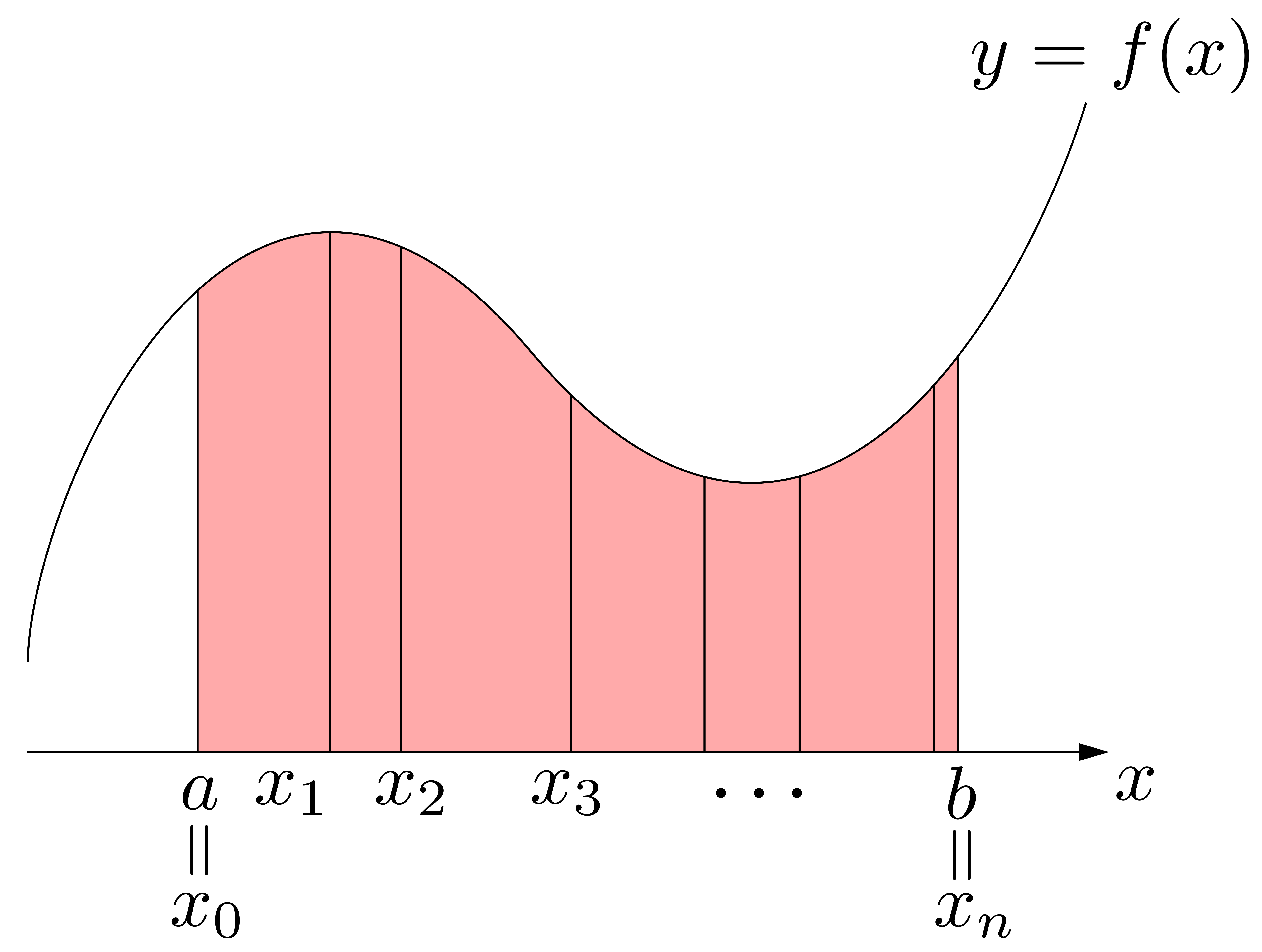
次に,これら\(n\)個の図形を,長方形に近似します.区間\([x_{i-1},~x_{i}]\)において「高さ」をとる\(x\)を\(\xi_i\)とします.区間\([x_{i-1},~x_{i}]\)上のどの点\(x\)を\(\xi_i\)とするかは任意です(ちなみに\(\xi\)はギリシャ文字で「グザイ」「クシー」などと読みます).
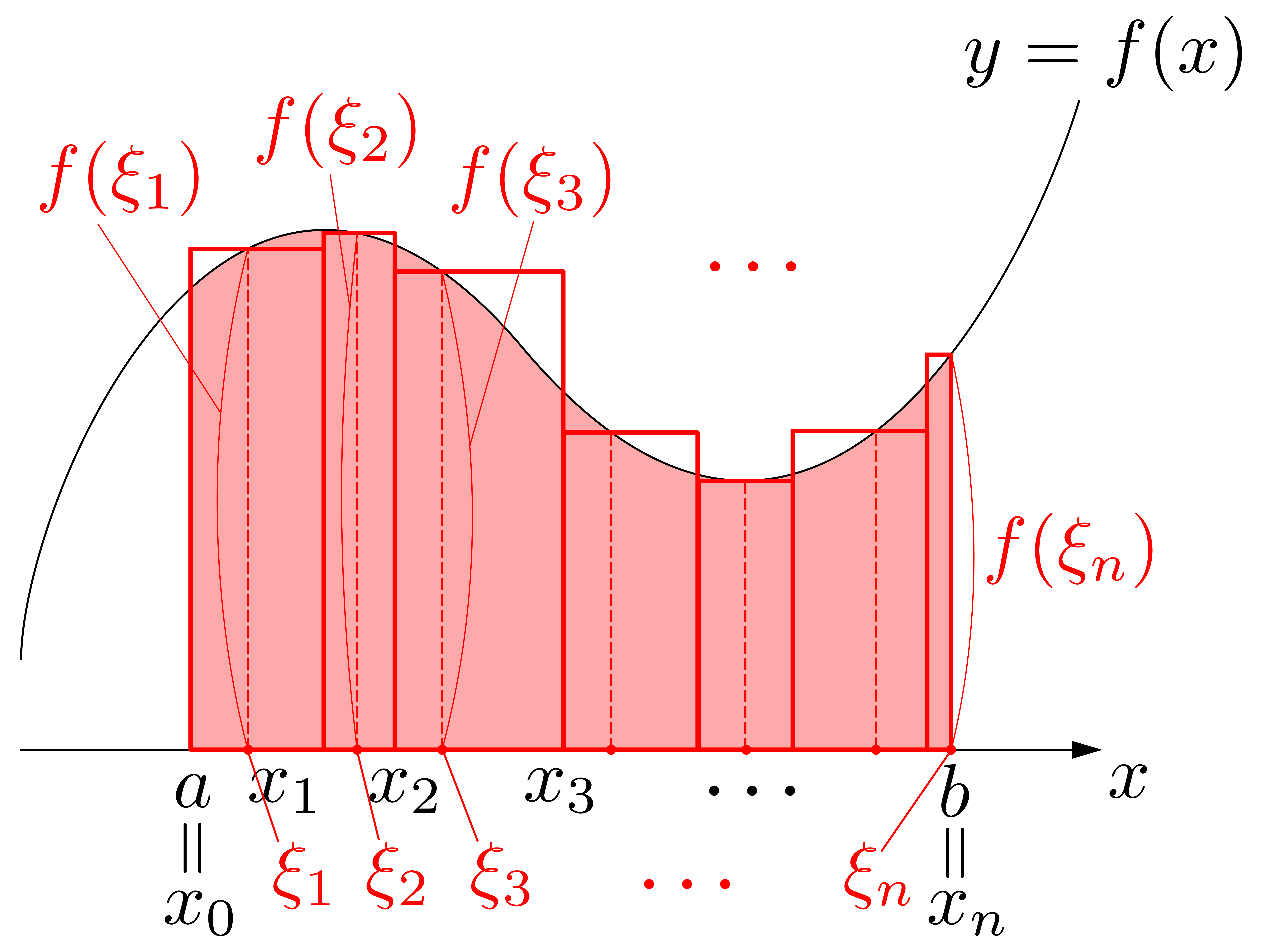
これらの長方形の面積を求めます.例えば左から\(i\)番目の長方形の面積なら,横幅は\(x_{i}-x_{i-1}\)です.高さは\(f(\xi_i)\)です.したがって左から\(i\)番目の長方形の面積は
\[f(\xi_i)(x_{i+1}-x_i)\]
と書けます.さらに,\(x_{i+1}-x_i=\Delta x_i\)とおけば,
\[f(\xi_i)\Delta x_i\]
と書けます.これを\(n\)個寄せ集めるのですから,敷き詰めた長方形の面積の和は
\[\sum^{n}_{i=0}f(\xi_i)\Delta x_i\]
と表されることになります.これをリーマン和と呼びます.
この「リーマン和」をもってして図形Aの「面積」とするのはどうでしょうか?…それはちょっとマズイ気がします.なぜなら,図形Aとリーマン和とではスキマ(誤差)が大きすぎますから(下図参照).

どうすればスキマ(誤差)は小さくなるでしょうか?各長方形の幅を小さくすれば,細長い長方形になって,スキマは小さくなります.当然,スキマは小さければ小さいほど,今私たちにとって欲しいものが正確に求まりそうな気がします.各長方形の幅を小さくするには,\(n\)を大きく,すなわち分割の数を大きくしてやればいいでしょう.
式で表すと,
\[\lim_{n\rightarrow \infty}\sum^{n}_{i=0}f(\xi_i)\Delta x_i\]
これなら,図形の「面積」と呼んでも差し支えなさそうです.そこで,この極限値を図形Aの「面積」と定義し,「定積分」と名付け,記号\[\int^b_a f(x)dx\]で表すことにします.
\(:=\)は「左辺を右辺で定義する」という意味です.
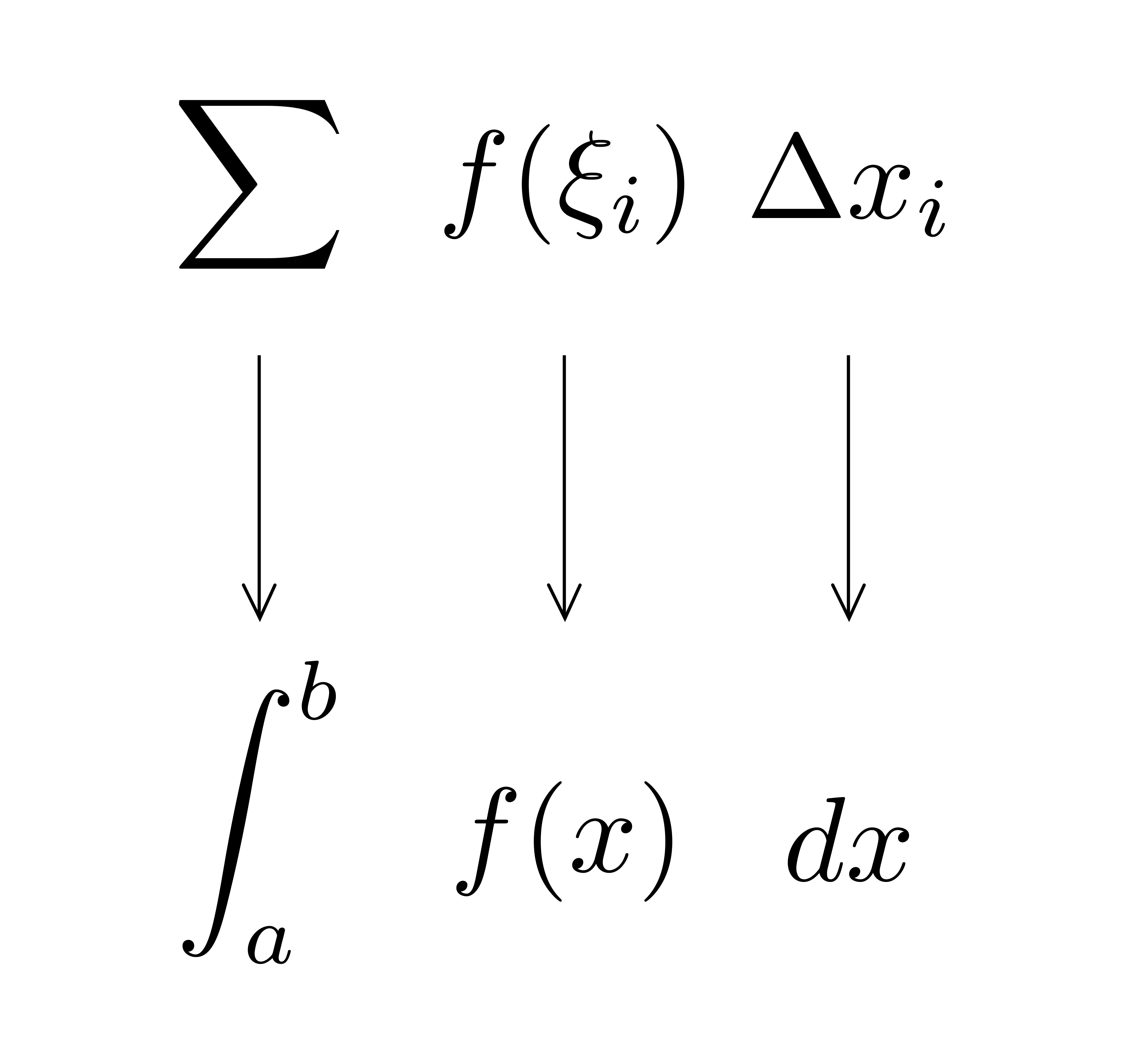 以上を見ると,\(\displaystyle \int^b_a f(x)dx\)の\(\displaystyle \int\)や\(dx\)の「イメージ」が見えてきます.右図に示すように,\(\displaystyle \sum\)が\(\displaystyle \int\)に,\(\Delta x_i\)が\(dx\)と対応しているわけです.
以上を見ると,\(\displaystyle \int^b_a f(x)dx\)の\(\displaystyle \int\)や\(dx\)の「イメージ」が見えてきます.右図に示すように,\(\displaystyle \sum\)が\(\displaystyle \int\)に,\(\Delta x_i\)が\(dx\)と対応しているわけです.
ここで,\(\displaystyle \sum\ f(\xi_i)\Delta x_i\)の意味を思い出しましょう.\(f(\xi_i)\)が「タテ」,\(\Delta x_i\)が「ヨコ」を表すのでしたから,\(f(\xi_i)\times\Delta x_i\)は「長方形の面積」を意味し,その長方形の面積\(f(\xi_i)\Delta x_i\)を\(\displaystyle \sum\)する(足し加える),という意味でした.
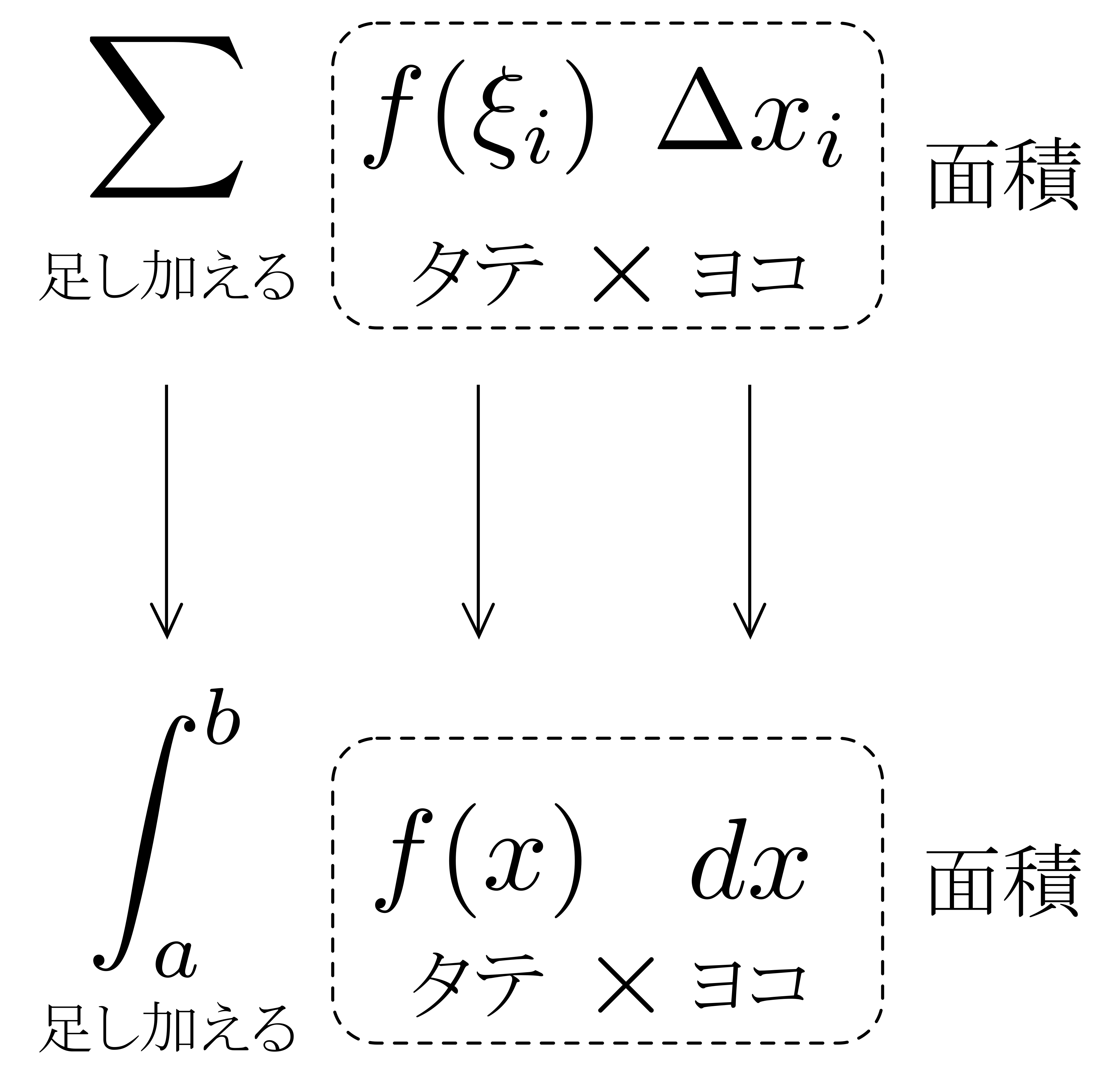 以上を踏まえて\(\displaystyle \int^b_a f(x)dx\)を眺めると,これは「微小面積\(f(x)\times dx\)を\(\displaystyle \int\)したもの(連続的に足し加えたもの)」と読み取れることが分かります!
以上を踏まえて\(\displaystyle \int^b_a f(x)dx\)を眺めると,これは「微小面積\(f(x)\times dx\)を\(\displaystyle \int\)したもの(連続的に足し加えたもの)」と読み取れることが分かります!
定積分を「リーマン和の極限」とみなす捉え方は,とても自然で,記号の導入も全く違和感がありません.さらに,右図に示した記号の解釈は,定積分の問題を扱う上で極めて重要な解釈になります.
次回はこの定積分の定義に従って図形の面積を計算してみます.すると,大きな問題に直面します….



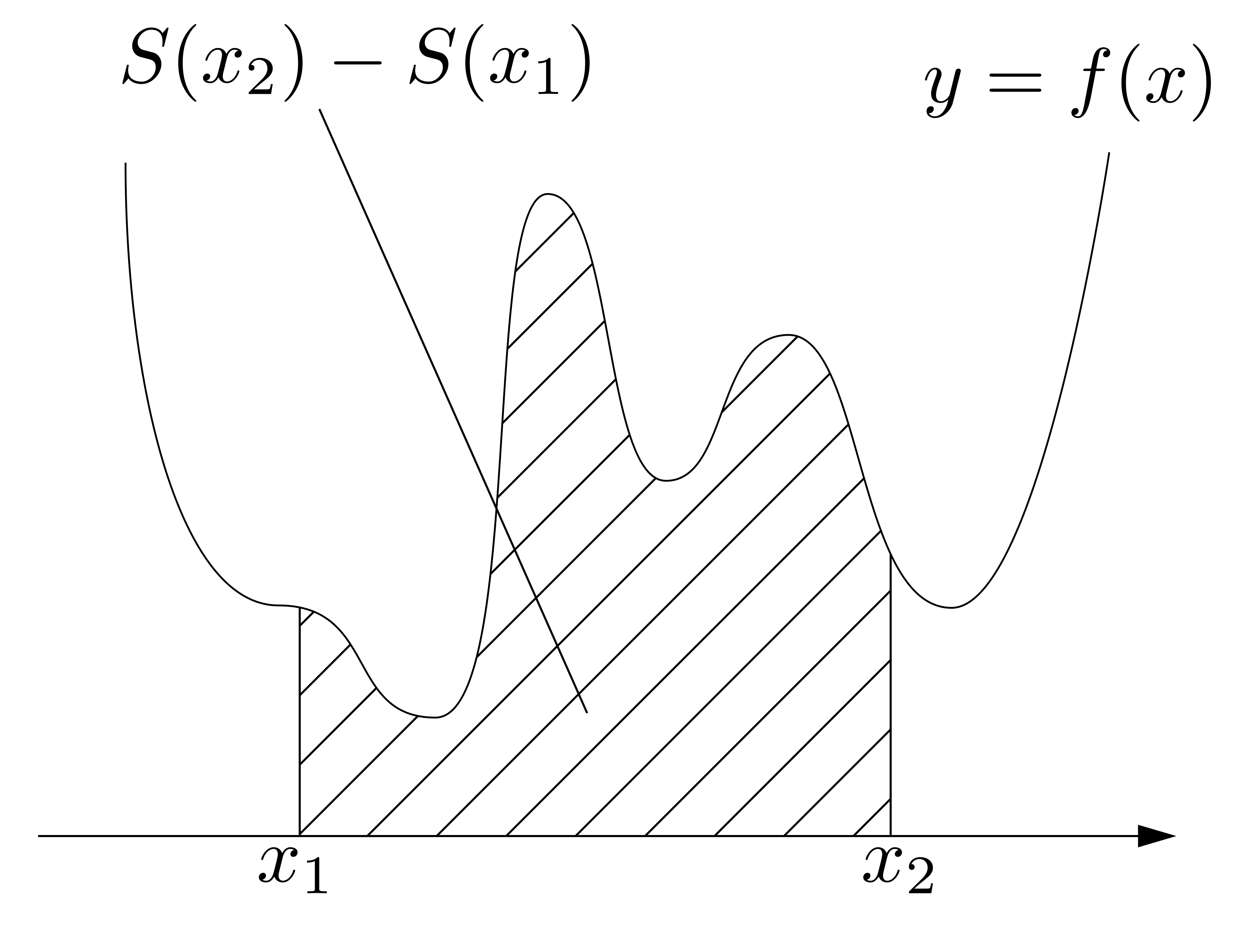

 問題
問題