youtubeのおもしろ動画。これを不思議と思うか，あるいは一目でツッコミを入れられるかどうか，論理の勉強になる動画だと思います。
（\(0=1\)の証明？）
\begin{align}
-20 &=-20 \tag{1}\\
16-36 &= 25-45 \tag{2}\\
4^2-4\cdot 9 &= 5^2 – 5\cdot 9 \tag{3}\\
4^2-4\cdot 9 + \frac{81}{4} &= 5^2 – 5\cdot 9 + \frac{81}{4} \tag{4}\\
4^2-2 \cdot 4\cdot \frac{9}{2} + \left(\frac{9}{2}\right)^2 &= 5^2 – 2 \cdot 5\cdot \frac{9}{2} + \left(\frac{9}{2}\right)^2 \tag{5}\\
\left(4 – \frac{9}{2}\right)^2&= \left(5 – \frac{9}{2} \right)^2 \tag{6}\\
4 – \frac{9}{2}&= 5 – \frac{9}{2} \tag{7}\\
4 &= 5 \tag{8}\\
4 -4 &= 5 – 4 \tag{9}\\
0 &= 1 \tag{10}
\end{align}私たちは一般に計算問題が与えられば式を次々と改行・羅列して「答え」を求め，とにもかくにも「答え」さえ手に入れば，とくに疑問も抱くことなくそれを解答欄に書いてさっさと次の問題に進みがちです。しかし，細かいことをいえば本来はその各行の式と式の間には論理的にどういう関係があるのか，まで考える必要があります：
たとえば，\(-20 =-20\)と\(16-36 = 25-45 \)の間にはどんな関係があるでしょうか。\(16-36=-20\)そして\(25-45=-20\)という等式が成り立ちますから，\(-20 =-20 \)という仮定から\(16-36 = 25-45 \)が導けます。すなわち，\[-20 =-20 \Longrightarrow 16-36 = 25-45\]逆に，\(16-36 = 25-45 \)という仮定から\(-20 =-20 \)も確かに導けます。\[-20 =-20 \Longleftarrow 16-36 = 25-45\]この二つをあわせて，\[-20 =-20 \Longleftrightarrow 16-36 = 25-45\]と書きます。
式\((1)\)と式\((2)\)はいわば互いに‘行き来’できる関係（これを以後「同値」と呼ぶことにします）がありましたが，一般には必ずしもこのような関係が成り立つとは限りません（感覚的にたとえると「犬ならば哺乳類」ですが「哺乳類ならば犬」とは限りません）。この点に注意して，各行における「式と式の論理関係」を同様に調べていくと\((1)\)から\((6)\)までの式，また\((7)\)から\((10)\)までの式が互いに同値であることは一目でわかります。怪しいのは\((6)\)式と\((7)\)式の間の論理関係です。見た目がうるさいので，ここでは\(4 – \frac{9}{2} = a\)，\(5 – \frac{9}{2} = b\)とおいて考えることにします。
\(a^2=b^2 \Leftarrow a=b\)は言えるか？
これは明らかに言えます。仮定\(a=b\)の両辺を\(2\)乗すればいいだけですから。
\(a^2=b^2 \Rightarrow a=b\)は言えるか？
これはいけない。なぜなら，\(a^2=b^2\)という仮定からは，\(a=b\)だけでなく，\(a=-b\)という可能性も考えられますから。実際，
\begin{align*}
&a^2=b^2\\
\Longrightarrow~&a^2-b^2=0\\
\Longrightarrow~&(a-b)(a+b)=0\\
\Longrightarrow~&a-b=0\text{または}a+b=0\\
\Longrightarrow~&a=b\text{または}a=-b
\end{align*}（※逆も成り立つ）
以下，正しい論理（式）を書いてみます（または，を\(\lor\)と書くことにします）。
\begin{align}
&-20 =-20 \\
\Longleftrightarrow &~16-36 = 25-45 \\
\Longleftrightarrow &~4^2-4\cdot 9 = 5^2 – 5\cdot 9 \\
\Longleftrightarrow &~4^2-4\cdot 9 + \frac{81}{4} = 5^2 – 5\cdot 9 + \frac{81}{4} \\
\Longleftrightarrow &~4^2-2 \cdot 4\cdot \frac{9}{2} + \left(\frac{9}{2}\right)^2 = 5^2 – 2 \cdot 5\cdot \frac{9}{2} + \left(\frac{9}{2}\right)^2 \\
\Longleftrightarrow &~\left(4 – \frac{9}{2}\right)^2= \left(5 – \frac{9}{2} \right)^2 \\
\Longleftrightarrow &~4 – \frac{9}{2}= 5 – \frac{9}{2} \lor 4 – \frac{9}{2}= – \left( 5 – \frac{9}{2}\right)\\
\Longleftrightarrow &~4 = 5 \lor 9 = 9 \\
\Longleftrightarrow &~9 = 9\\
\end{align}結局，\((1)\)から\((5)\)はいわば‘目くらまし’で，\(-20=-20\)という面白みのない仮定から，\(9=9\)というやはり面白みのない結論が得れらた，ということに過ぎない，ということでした。
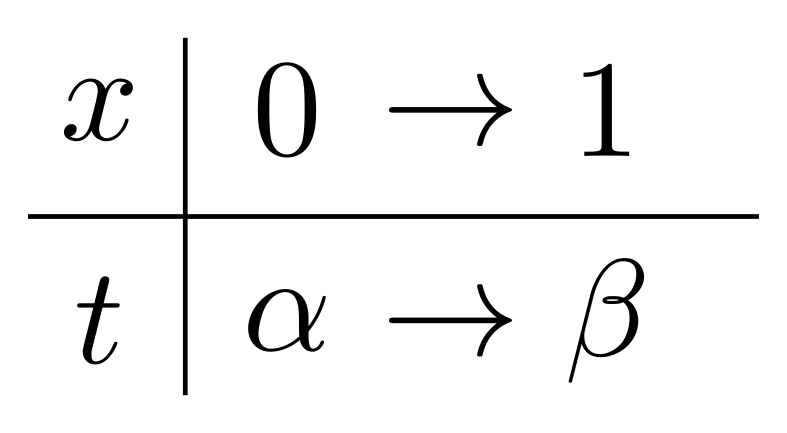さて次に，\(\displaystyle \int^1_0x^{p-1}(1-x)^{q-1}dx\)の積分区間\([0,~1]\)が，\([\alpha,~\beta]\)となるような置換を考えてみましょう．すなわち右のような置換です（新たな変数\(t\)としました）．この場合，どのように置換すればよいでしょうか？\(t\)が\(\alpha\)のとき\(x\)が\(0\)ですから，さしあたり\[x=t-\alpha\]という置換が思い浮かびます．しかし，\(t=\beta\)のとき\(x\)は\(\beta-\alpha\)ではなく\(1\)であってほしい．であれば，\(t-\alpha\)を\(\beta-\alpha\)で割ればいいのでは？と考え，\[\displaystyle x=\frac{t-\alpha}{\beta-\alpha}\]という置換に気付きます．置換してみましょう．\(\displaystyle dx=\frac{1}{\beta-\alpha}dt\)ですから，