タグ: 円と放物線

次の解答は誤りです。

誤りの理由をかけ，という問題について考えてみます。この問題の模範解答は

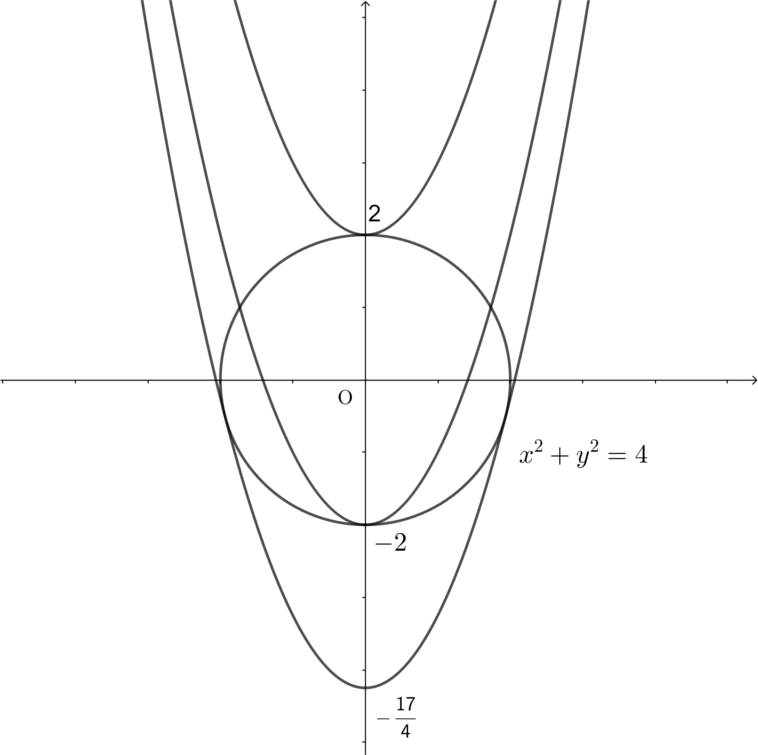
\((1)\)より\(x^2=3-y^2\)．したがって\(3-y^2\geq 0 \Leftrightarrow -\sqrt{3}\leq y \leq \sqrt{3}\)．しかし得られた重解\(y=-3\)はこの式を満たさない。ゆえに連立方程式\((1),(2)\)は実数解をもたない．つまり，\((1)\)と\((2)\)の共有点は存在しない．

という「連立方程式\((1)\)\((2)\)を解いても解がないから，共有点はない。だから接するなんてことはありえない」というものでしたが，ここでは違う視点から誤りを指摘してみます。まず，話を整理するために，「接する」ことの定義を確認しておきます：

また，次を証明しておきます。

証明

（\(\Rightarrow\)）
\begin{align*}
&y=f(x)\text{と}y=g(x)\text{が接する}\\
\overset{\text{def}}{\Longleftrightarrow}~&\exists a [f(a)=g(a),~f^{\prime}(a)=g^{\prime}(a)]\\
\Longleftrightarrow~&\exists a [f(a)-g(a)=0,~(f(a)-g(a))^{\prime}=0]\\
\Longleftrightarrow~&\exists a\begin{cases}
f(a)-g(a)=0 \\
(f(a)-g(a))^{\prime}=0
\end{cases}
\end{align*}\(f(x)-g(x)\)は多項式であるから，因数定理により\[f(x)-g(x)=(x-a)Q(x)\]と変形できる．辺々微分して\[(f(x)-g(x))^{\prime}=Q(x)+(x-a)Q^{\prime}(x)\]この式と第2式により\[Q(x)=-(x-a)Q^{\prime}(x)\]を得る．これを最初の式に代入して\[f(x)-g(x)=-(x-a)^2Q^{\prime}(x)\]したがって\(f(x)-g(x)=0\)は重解をもつ．

（\(\Leftarrow\)）

重解を\(a\)とする．仮定により\[f(x)-g(x)=(x-a)^2Q(x)\]とおける．\(x=a\)と代入して\[f(a)-g(a)=0 \Leftrightarrow~f(a)=g(a)\]また，辺々微分して\[f^{\prime}(x)-g^{\prime}(x)=2(x-a)Q(x)+(x-a)^2Q^{\prime}(x)\]これに\(x=a\)と代入して\[f^{\prime}(a)-g^{\prime}(a)=0 \Leftrightarrow~f^{\prime}(a)=g^{\prime}(a)\]ゆえに\(y=f(x)\)と\(y=g(x)\)は接する．

証明終

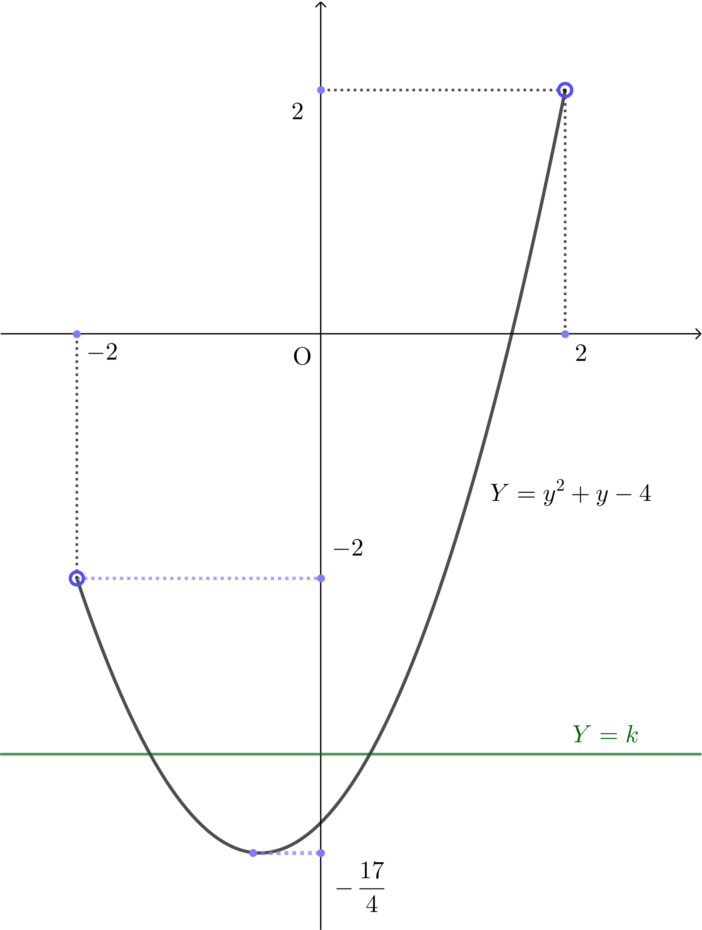
さて，ここで誤答の「重解をもつから，\((1)\)と\((2)\)は接する」の部分を考えてみると，まず「重解をもつから」の主語が連立した結果の式\[y=\frac{1}{6}(3-y^2)-2\]であることが気になります。接するための十分条件は，多項式\(y=f(x),y=g(x)\)について「\(f(x)-g(x)=0\)が」重解をもつ，であったはずです。したがってまず\(y=f(x),y=g(x)\)という式を用意しなければならない。しかし\(y=\frac{1}{6}x^2-2\)はさておき\(y=\pm\sqrt{1-x^2}\)は多項式ではない。仮定を満たしていない以上，上の定理は使えない（実際，定理の証明を見ると分かるように「多項式」を仮定しないと因数定理も使えないしそもそも重解を定義できない）。

なので，個人的には「実際に調べてみると接しないよね」というより「重解をもつから，接する」という主張（というか理解）のいい加減さ曖昧さを指摘したい。「『どの式が』重解をもつの？」「『その式』が重解をもつことと接することに何の関係があるの？」と問いたい。

「接するときたら重解条件！」のような参考書でよく見るスローガン的解法は，付け焼き刃的には有効かもしれませんが，「接する」とは具体的にどういう状態を指すのか（定義），そして「接する」ことと「重解」をもつことはそれぞれ十分なのか必要なのか，「何が」重解をもつのか，またそれらは何を仮定しているのか，などを考えずにいい加減な理解で使っていると表面上はもっともらしい解答が作れてもよく見るとめちゃくちゃな気持ち悪い解答になる。

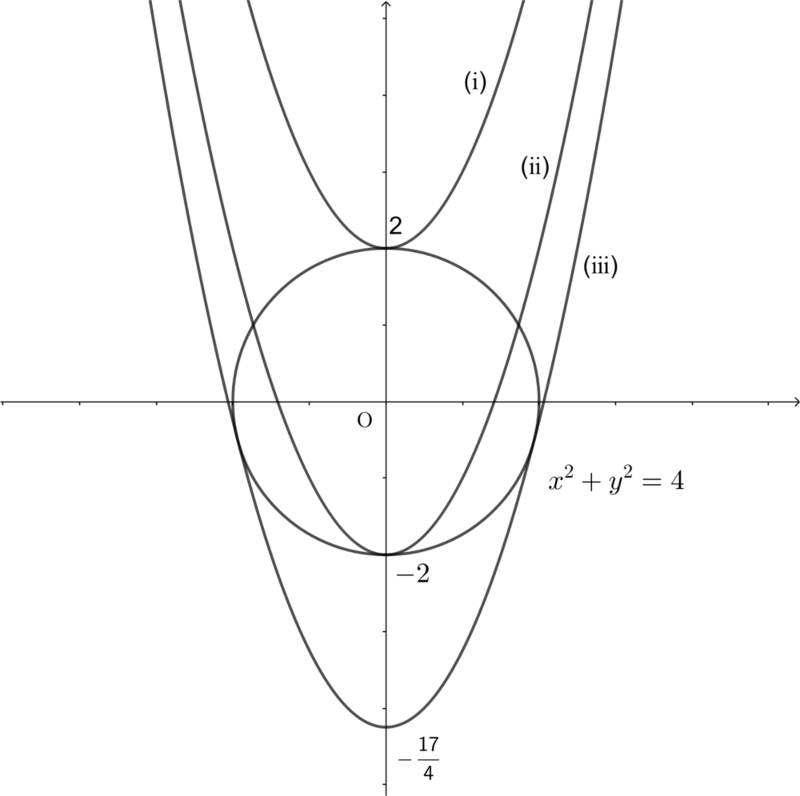
というわけで，円と2次曲線の問題では安易に「重解条件」は使ってはいけない。これは肝に銘じておくべきだと思います。

円と放物線が共有点をもつときの\(k\)の範囲を\(\mathcal{D}\)とおく．
\begin{align*}
&k\in\mathcal{D}\\
\Longleftrightarrow~ &\exists x \exists y \begin{cases}x^2+y^2=4 \\ y=x^2+k\end{cases}\\
\Longleftrightarrow~ &\exists x \exists y \begin{cases}x^2+y^2=4 \\ y=(4-y^2)+k\end{cases}\\
\Longleftrightarrow~ &\exists x \exists y \begin{cases}x^2=4-y^2 \\ y^2+y-4-k=0\end{cases}\\
\Longleftrightarrow~ &\exists y\left[\exists x [x^2=4-y^2] \land y^2+y-4-k=0 \right]\\
\Longleftrightarrow~ &\exists y\left[-2 \leq y \leq 2 \land y^2+y-4=k \right]\\
\Longleftrightarrow~ &\exists y\left[-2 \leq y \leq 2 \land \left(y+\frac{1}{2}\right)^2-\frac{17}{4}=k \right]\\
\Longleftrightarrow~ &-\frac{17}{4} \leq k \leq 2 \tag{\(\ast\)}
\end{align*}
\((2)~\)上の結果と下図から，接するとき，\(k=\pm 2\)または\(k=-\frac{17}{4}\)．

\((1)~\)\((2)\)の考察と上図から，異なる\(4\)つの共有点をもつとき，\(-\frac{17}{4} < k < -2\)．

\((\ast)\)の考察は下図による（文字定数は分離せよ，の方針）．

\(\rm(i\hspace{-.08em}i\hspace{-.08em}i)\)のとき．
\begin{align*}
&\text{円と放物線が接する}\\
\overset{def}{\Longleftrightarrow}~&\text{円と放物線が\(1\)点\(\mathrm{T}\)を共有し，点\(\mathrm{T}\)における両者の接線が一致する}\\
\Longleftrightarrow~&\text{放物線上の点\(\mathrm{T}\)を通り，その点における接線に垂直な直線が円の中心を通る}\\
\end{align*}
であることに着目する．\(\mathrm{T}(t,t^2+k)\)とおく．放物線上の点\(\mathrm{T}\)を通り，その点における接線に垂直な直線の方程式は\((t^2+k)’=2t\)であることから
\[y-(t^2+k)=-\frac{1}{2t}(x-t)\]
とかける．これが原点を通るから，
\[0-(t^2+k)=-\frac{1}{2t}(0-t) \Longleftrightarrow t^2=-k-\frac{1}{2}\]
これを満たす\(t\)が存在すればよいから（点\(\mathrm{T}\)は円上の点であることにも注意して），
\begin{align*}
&\exists t\begin{cases}t^2+(t^2+k)^2=4 \\ t^2=-k-\frac{1}{2}\end{cases}\\
\Longleftrightarrow~& \exists t\begin{cases}\left(-k-\frac{1}{2}\right)+\frac{1}{4}=4 \\ t^2=-k-\frac{1}{2}\end{cases}\\
\Longleftrightarrow~& \exists t\begin{cases}k=-\frac{17}{4}\\ t^2=-k-\frac{1}{2}\end{cases}\\
\Longleftrightarrow~& \exists t\left[k=-\frac{17}{4} \land t^2=\frac{15}{4}\right]\\
\Longleftrightarrow~& k=-\frac{17}{4} \land \exists t\left[t^2=\frac{15}{4}\right]\\
\Longleftrightarrow~& k=-\frac{17}{4}
\end{align*}

「円と放物線」の定番問題です．多くの解答では「重解条件」を用いていますが，どこか気持ち悪い．「重解条件」を使わない解法について見てみます．

\((2)\)別解

図により，
\[\text{接する}~\Longleftrightarrow \rm(\hspace{.18em}i\hspace{.18em})\text{または}\rm(\hspace{.08em}ii\hspace{.08em})\text{または}\rm(i\hspace{-.08em}i\hspace{-.08em}i)\]である．

\(\rm(\hspace{.18em}i\hspace{.18em})\)のとき，図より明らかに\(k=2\)．逆も成り立つ．

\(\rm(\hspace{.08em}ii\hspace{.08em})\)のとき，図より明らかに\(k=-2\)．逆も成り立つ．

\(\rm(i\hspace{-.08em}i\hspace{-.08em}i)\)のとき．
\(y=x^2+k\)上の点を\(P(s,s^2+k)\)とおく．線分\(OP\)を調べる．
\begin{align*}
OP^2=&s^2+(s^2+k)^2\\
=&t+(t+k)^2&(s^2=t\text{とおいた})\\
=&t^2+(2k+1)t+k^2\\
=&\left(t+k+\frac{1}{2}\right)^2-k-\frac{1}{4}&(t\geq 0)\\
\end{align*}
図より\(k<-2\)であるから\[-k-\frac{1}{2} > \frac{3}{2}\]
であることに注意すると，\(OP^2\)の最小値は\(-k-\frac{1}{4}\)．これが円の半径\(2\)と一致するとき，かつそのときに限り円と放物線は\(\rm(i\hspace{-.08em}i\hspace{-.08em}i)\)のように接する．したがって
\[\sqrt{-k-\frac{1}{4}}=2\Longleftrightarrow k=-\frac{17}{4}\]
以上により求める条件は\(k=\pm 2\)または\(k=-\frac{17}{4}\)となる．

\(\ast\)　　　　\(\ast\)　　　　\(\ast\)

（\(\rm(i\hspace{-.08em}i\hspace{-.08em}i)\)の別解はこちら）