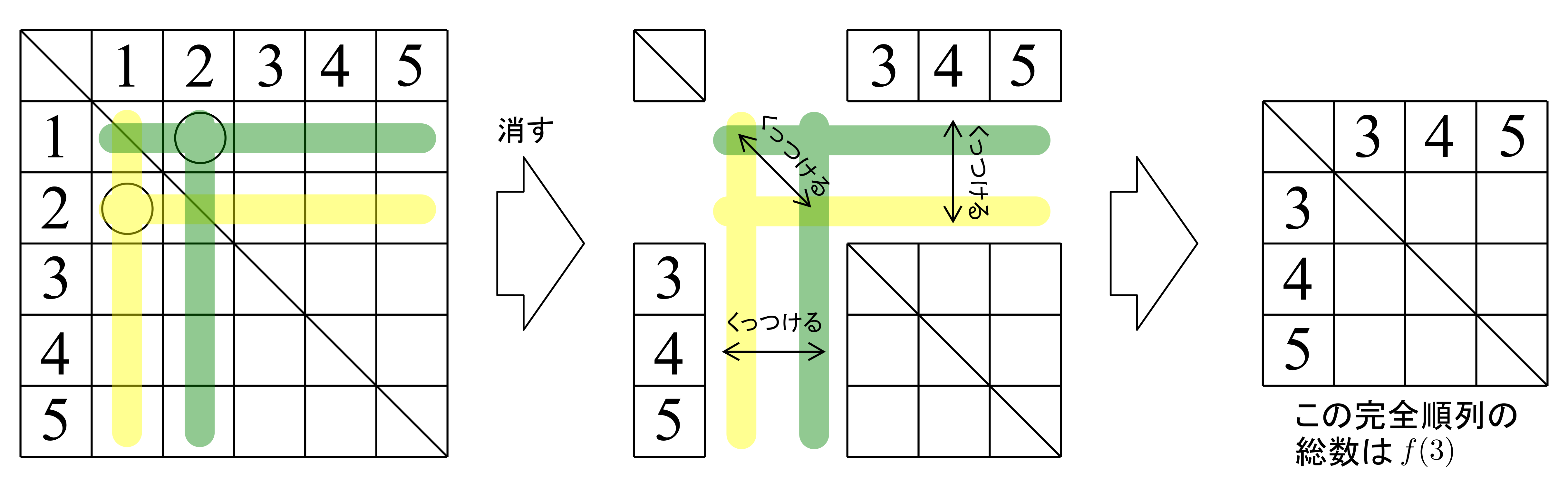
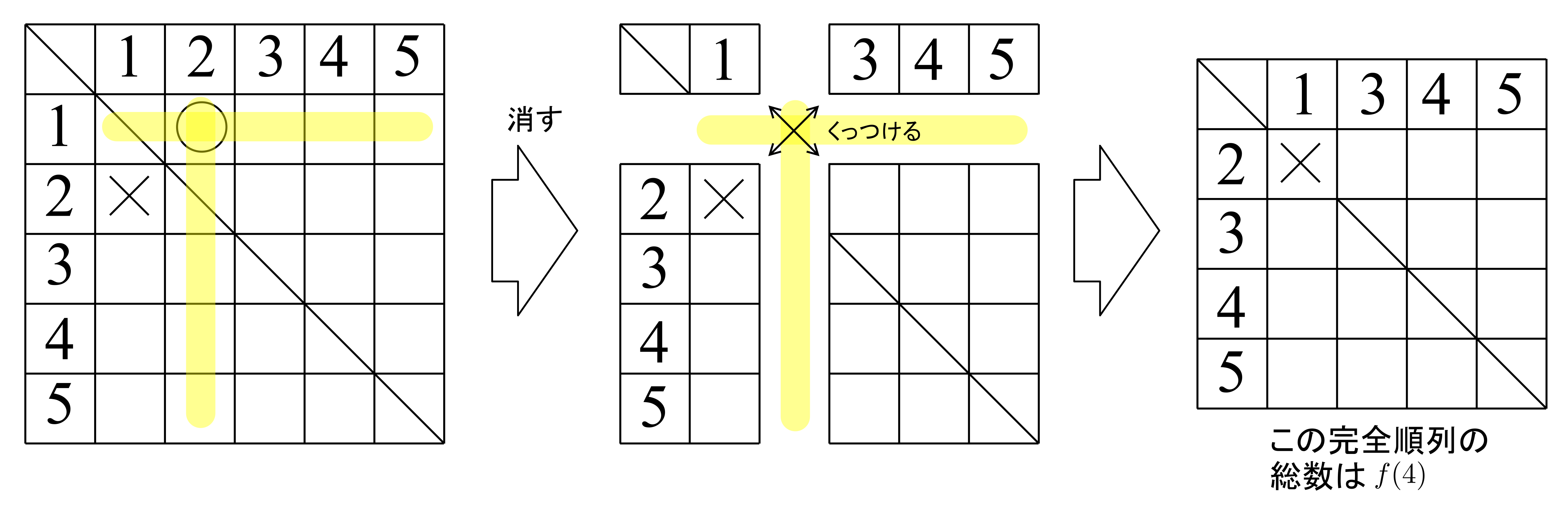
「\(n\)人のプレゼント交換会」ならどうでしょうか?この場合の完全順列の総数を求めてみましょう.
以下,\(i\)は自然数とします.
完全順列とは,「\(i\)番目に\(i\)が来ないような並び方\((1\leq i \leq n)\)」,すなわち\[\text{\(1\)以上\(n\)以下のすべての\(i\)に対して,\(i\)番目に\(i\)が来ない}\quad\cdots(\ast)\]という意味でした.この総数を求めたい,というわけですね.
今まで見てきた通り,これが一筋縄ではいかない問題でした.まして今回は\(n\)人です.そこで,お馴染みのアイデア:直接求めるのが難しいのなら,全体からその否定を除けばいい,という「余事象」の考え方で攻めてみることにしましょう.というわけで,\((\ast)\)の否定を考えてみます.
「すべての」の否定は「存在する」でしたから(なぜ?),\((\ast)\)の否定は次のようになります.\[\text{\(i\)番目が\(i\)になる\(1\)以上\(n\)以下の\(i\)が存在する}\quad\cdots(\ast\ast)\]
この総数を数え,そして並べ替えの総数\(n!\)から引いてやりましょう.ここで,\(i\)番目が\(i\)となるような事象を\(A_i~(1\leq i \leq n)\)とおくことにします.すると\((\ast\ast)\)となる総数は
\[n(A_1\cup A_2\cup A_3 \cup \cdots \cup A_n)=n \left( \bigcup^n_{i=1}A_i \right)\]と表せることになります.したがって,求める完全順列の総数は
\[n!-n\left(\bigcup^n_{i=1}A_i\right)\]
となります.さて,この式の二項目\(n(\bigcup^n_{i=1}A_i)\)ですが,これは以下のように計算できます(なぜ?).
\[
n\left(\displaystyle\bigcup_{i}^{n} A_i\right)=\displaystyle\sum_{i}^{n} n(A_i)-\displaystyle\sum_{i<j}^{n}n(A_i \cap A_j)+\displaystyle\sum_{i<j<k}^{n}n(A_i \cap A_j \cap A_k)-\cdots+(-1)^{n-1}\displaystyle\sum^{n}_{i<j<\cdots} n(A_i \cap A_j \cap \cdots )
\]
ここで,\[\displaystyle\sum_{i}^{n} n(A_i),~\sum_{i<j}^{n}n(A_i \cap A_j),~\sum_{i<j<k}^{n}n(A_i \cap A_j \cap A_k),\cdots,\sum^{n}_{i<j<\cdots} n(A_i \cap A_j \cap \cdots)\]を求めてみると,
\[
\begin{align*}
&\displaystyle\sum_{i}^{n} n(A_i)={ }_n\mathrm{C}_1\times (n-1)!\\
&\sum_{i<j}^{n}n(A_i \cap A_j)={ }_n\mathrm{C}_2\times(n-2)!\\
&\sum_{i<j<k}^{n}n(A_i \cap A_j \cap A_k)={ }_n\mathrm{C}_3\times(n-3)!\\
&\qquad\qquad\vdots\\
&\sum^{n}_{i<j<\cdots} n(A_i \cap A_j \cap \cdots)={ }_n\mathrm{C}_n\times(n-n)!
\end{align*}
\]
ですから結局,
\[n\left(\displaystyle\bigcup_{i}^{n} A_i\right)={ }_n\mathrm{C}_1\times (n-1)!-{ }_n\mathrm{C}_2\times(n-2)!+{ }_n\mathrm{C}_3\times(n-3)!-\cdots+(-1)^{n-1}{ }_n\mathrm{C}_n\times(n-n)!\]
よって,求める完全順列の総数は,
\[
\begin{align*}
n!-n\left(\bigcup^n_{i=1}A_i\right)=~&n!-\left({ }_n\mathrm{C}_1\times (n-1)!-{ }_n\mathrm{C}_2\times(n-2)!+{ }_n\mathrm{C}_3\times(n-3)!-\cdots+(-1)^{n-1}{ }_n\mathrm{C}_n\times(n-n)!\right)\\
=~&n!-\left(\frac{n!}{1!}-\frac{n!}{2!}+\frac{n!}{3!}-\cdots+(-1)^{n-1}\frac{n!}{n!} \right)\\
=~&n!-\frac{n!}{1!}+\frac{n!}{2!}-\frac{n!}{3!}+\cdots+(-1)^{n}\frac{n!}{n!} \\
=~&n!\left(1-\frac{1}{1!}+\frac{1}{2!}-\frac{1}{3!}+\cdots+(-1)^{n}\frac{1}{n!}\right)\\
=~&n!\sum^{n}_{k=0}\frac{(-1)^k}{k!}\\
\end{align*}
\]
となります.
実験してみましょう.\(n=5\)と代入してみます.
\[
\begin{align*}
5!\sum^{5}_{k=0}\frac{(-1)^k}{k!}&=5!\left(1-\frac{1}{1!}+\frac{1}{2!}-\frac{1}{3!}+\frac{1}{4!}-\frac{1}{5!}\right)\\
&=5\cdot 4\cdot 3-5\cdot 4 +5-1\\
&=60-20+5-1\\
&=44
\end{align*}
\]
おっけい!