タグ: 正射影ベクトル

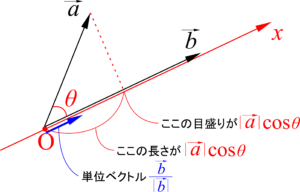
点と直線の距離の公式を証明してみましょう．

直線\(l:ax+by+c=0\)と，この直線上にない点を\(\mathrm{P}(x_0,~y_0)\)，そして下図に示す直線\(l\)上の点を\(\mathrm{A}(p,~q)\)とします．

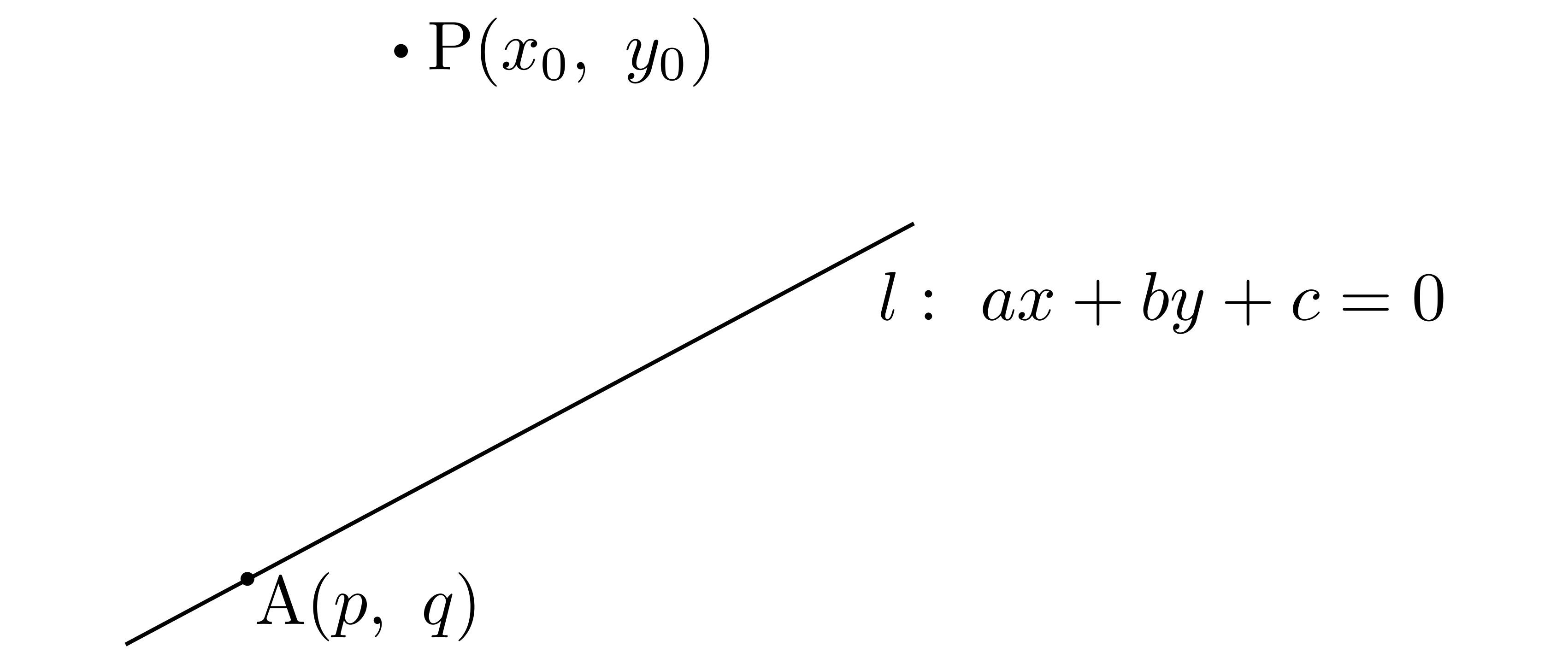
まず\(l\)の法線ベクトルを求め，図示します．法線ベクトルは\(x\)と\(y\)との係数から\((a,~b)\)でしたね（なぜ？）．また，\(\overrightarrow{\mathrm{AP}}\)を図示しておきます．（下図では\((a,~b)\)を列ベクトルで表記しています．）

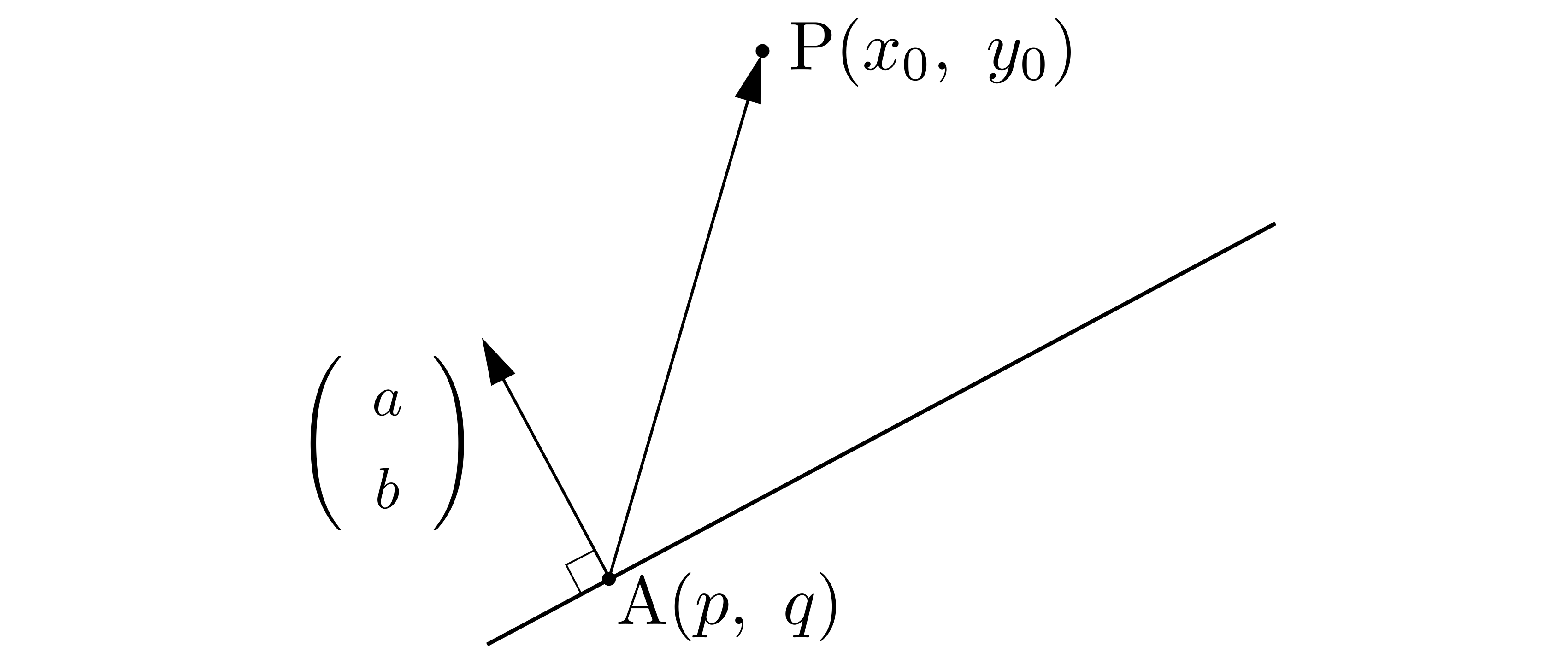
求めたいものも図示しておきましょう．それは，

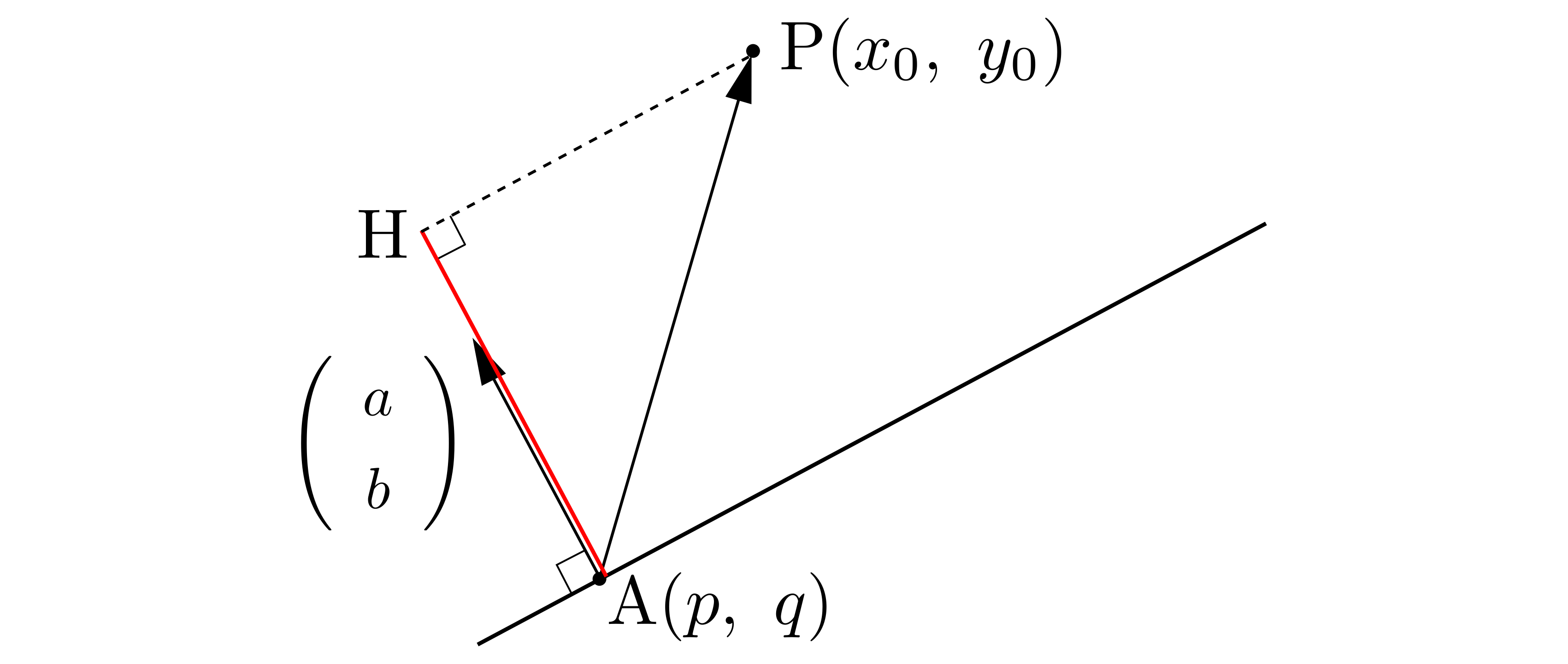
上図の赤い線分\(\mathrm{AH}(=|\overrightarrow{\mathrm{AH}}|)\)ですね．

気づいたでしょうか？これはほかならぬ正射影ベクトル（の大きさ）です．ですから結局，「点と直線の距離は，正射影ベクトルを求めて，その大きさを求めればよい」と分かります．

ここで正射影ベクトルの公式の出番です！

正射影ベクトルを求めるために，ベクトル\((a,~b)\)を正規化（大きさを１にすること）しておきましょう：
\[\frac{1}{\sqrt{a^2+b^2}}
\left(\begin{array}{c}
a \\
b \\
\end{array}\right)
\]
このベクトルを\(\overrightarrow{n}\)とおきます．すると，正射影ベクトルの公式から，\(\overrightarrow{\mathrm{AH}}\)は\[(\overrightarrow{\mathrm{AP}}\cdot\overrightarrow{n})\overrightarrow{n}\]と書けますね．\[\overrightarrow{\mathrm{AP}}=\left(\begin{array}{c} x_0\\ y_0\end{array}\right)-\left(\begin{array}{c} p\\ q\end{array}\right)=\left(\begin{array}{c} x_0-p\\ y_0-q\end{array}\right)
\]
ですから，計算すると
\[
\begin{align*}
&\overrightarrow{\mathrm{AH}}=(\overrightarrow{\mathrm{AP}}\cdot\overrightarrow{n})\overrightarrow{n}\\
=&\left\{\left(\begin{array}{c} x_0-p\\ y_0-q\end{array}\right)\cdot\frac{1}{\sqrt{a^2+b^2}}
\left(\begin{array}{c}
a \\
b \\
\end{array}\right)\right\}\overrightarrow{n}\\
=&\frac{a(x_0-p)+b(y_0-q)}{\sqrt{a^2+b^2}}\overrightarrow{n}
\end{align*}
\]
\(\mathrm{AH}=|\overrightarrow{\mathrm{AH}}|\)ですから，\(\left| \overrightarrow{n}\right|=1\)であることに注意して，
\[
\begin{align*}
\mathrm{AH}=&|\overrightarrow{\mathrm{AH}}|\\
=&\left|\frac{a(x_0-p)+b(y_0-q)}{\sqrt{a^2+b^2}}\overrightarrow{n}\right|\\
=&\frac{|ax_0+by_0-ap-bq|}{\sqrt{a^2+b^2}}|\overrightarrow{n}|\\
=&\frac{|ax_0+by_0-ap-bq|}{\sqrt{a^2+b^2}}
\end{align*}
\]
ここで，\((p,~q)\)は直線\(l\)上の点でしたから，\[ap+bq+c=0\quad \text{すなわち}\quad c=-ap-bq\]が成り立ちます．したがって，上の式は結局
\[\mathrm{AH}=\frac{|ax_0+by_0+c|}{\sqrt{a^2+b^2}}\]となります．

この証明のいいところは，まず簡潔で記述量（計算量）が少ない（＝かっこいい）という点，それにこの公式の三次元バージョンとでもいいますか「点の平面の距離の公式」を導出する際もまったく同じように応用できるという点です．他にも，数学検定１級１次の問題でこのアイデアが使える問題がありました．いずれ紹介したいと思います．

また，この証明を通して「正射影ベクトルの公式」の使いどころも感じて貰えたかと思います．

今回はとりあえずここまでにして，「点と平面の距離の公式」も後ほど記事にしてみたいと思います．

ここに始点が揃った２つのベクトル\(\vec{a}\)と\(\vec{b}\)があります．\(\vec{a}\)による\(\vec{b}\)への落とした影となるベクトルを，「\(\vec{a}\)の正射影ベクトル」と呼びます．この\(\vec{a}\)の正射影ベクトルを求めてみましょう．

まず，\(\vec{b}\)と同じ向きの単位ベクトル\(\frac{\vec{b}}{|\vec{b}|}\)（下図青のベクトル）が１目盛りになるような軸（下図赤の軸）を設定します．このとき，正射影ベクトルの終点が指し示す場所の座標はいくらになるでしょうか．三角比の公式より，\(|\vec{a}|\cos\theta\)ですね．これは\(\theta\)が鈍角のときも成り立ちます．\[\text{正射影ベクトルの終点が指し示す座標は，}|\vec{a}|\cos\theta\text{で表される}\]

※ ここで「えっ？」と思った人は拡張された三角比の定義とそこから作られる定理（公式）が怪しい．定義を大切にしない人はこういうところで躓きます！※

したがって，単位ベクトル\(\frac{\vec{b}}{|\vec{b}|}\)に，この「座標」を掛けてやれば，正射影ベクトルが求まります．\[\text{正射影ベクトル}=\frac{\vec{b}}{|\vec{b}|}|\vec{a}|\cos\theta\]これで正射影ベクトルを表す式が手に入りました．

・・・と，上の式を公式としてもいいのですが，見た目がちょっと汚いので，もう少し手を加えてみましょう．上の単位ベクトル\(\frac{\vec{b}}{|\vec{b}|}\)を\(\vec{e}\)と表すことにして，さらに\(|\vec{a}|\cos\theta\)が
\[
\begin{align*}
|\vec{a}|\cos\theta&=|\vec{a}||\vec{e}|\cos\theta\\
&=\vec{a}\cdot\vec{e}
\end{align*}
\]
と表せることに注意すると，結局正射影ベクトルは，\[(\vec{a}\cdot\vec{e})\vec{e}\]とシンプルに記述できることになります．この結果は記憶に値します．というか常識にしておきたい知識です．なぜなら，「正射影ベクトル」が欲しくなるシチュエーションは入試その他で頻出だからです．

後日，この正射影ベクトルが使われる例を紹介してみたいと思います．