結論から言うと,合成の公式は覚える式ではありません.覚えても使い物になりません.そして忘れてしまえば終わりです.
\(a \sin \theta + b \cos \theta\)を合成してみます.以下のように「導く」のがおすすめです.
証明
まず\(\sin\theta,\cos\theta\)の係数\(a,b\)の二乗の和のルートをくくりだす.すなわち
\[
\begin{align*}
a \sin \theta + b \cos \theta &= \sqrt{a^2+b^2}\left(\frac{a}{\sqrt{a^2+b^2}}\sin \theta + \frac{b}{\sqrt{a^2+b^2}}\cos \theta\right)\\
\end{align*}
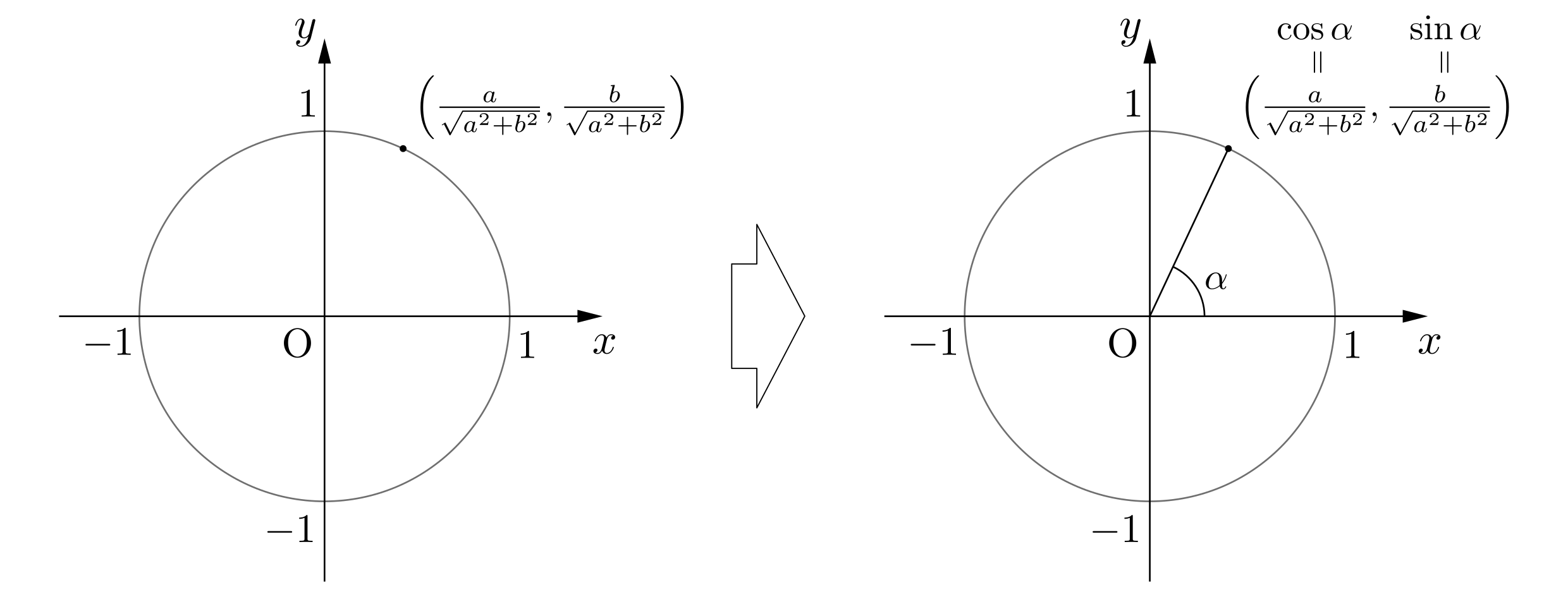
\]ここで,点\(\displaystyle \left(\frac{a}{\sqrt{a^2+b^2}},\frac{b}{\sqrt{a^2+b^2}}\right)\)は\(\displaystyle\left(\frac{a}{\sqrt{a^2+b^2}}\right)^2+\left(\frac{b}{\sqrt{a^2+b^2}}\right)^2=1\)をみたすことから単位円周上の点であるといえるので,その点と原点を結ぶ線分が\(x\)軸の正の方向となす角を\(\alpha\)とおけば
\[\frac{a}{\sqrt{a^2+b^2}}=\cos \alpha,~\frac{b}{\sqrt{a^2+b^2}}=\sin \alpha \tag{\(\ast\)}\]とおける.
 したがって
したがって
\[
\begin{align*}
a \sin \theta + b \cos \theta &= \sqrt{a^2+b^2}\left(\frac{a}{\sqrt{a^2+b^2}}\sin \theta + \frac{b}{\sqrt{a^2+b^2}}\cos \theta\right)\\
&=\sqrt{a^2+b^2}\left(\cos \alpha \sin \theta + \sin \alpha \cos \theta\right)\\
&=\sqrt{a^2+b^2}\left(\sin \theta \cos \alpha+\cos \theta \sin \alpha\right)
\end{align*}
\]
加法定理を逆向きに使うことで
\[=\sqrt{a^2+b^2}\sin(\theta + \alpha)\]
証明終
これは証明のための操作ではなく,実際に合成する際も上の証明と全く同じように考え,変形します.ですからこの証明を理解するということは,すなわち具体的な合成の手法が手に入ったということを意味します.また,上のように理解しておくと,たとえば\((\ast)\)において,点\(\displaystyle \left(\frac{b}{\sqrt{a^2+b^2}},\frac{a}{\sqrt{a^2+b^2}}\right)\)であっても\(\displaystyle\left(\frac{b}{\sqrt{a^2+b^2}}\right)^2+\left(\frac{a}{\sqrt{a^2+b^2}}\right)^2=1\)をみたすことからやはり単位円周上の点であるといえるので,\[\frac{b}{\sqrt{a^2+b^2}}=\cos \alpha’,~\frac{a}{\sqrt{a^2+b^2}}=\sin \alpha’\]ともおけることに気付きます.ここから上と同様の変形を行うと,
\[
\begin{align*}
a \sin \theta + b \cos \theta &= \sqrt{a^2+b^2}\left(\frac{a}{\sqrt{a^2+b^2}}\sin \theta + \frac{b}{\sqrt{a^2+b^2}}\cos \theta\right)\\
&=\sqrt{a^2+b^2}\left(\sin \alpha’ \sin \theta + \cos \alpha’ \cos \theta\right)\\
&=\sqrt{a^2+b^2}\left(\cos \theta\cos \alpha’ + \sin \theta\sin \alpha’\right)\\
&=\sqrt{a^2+b^2}\cos(\theta + \alpha’)
\end{align*}
\]とも変形できることに必然的に気付きます.
\(\ast\) \(\ast\) \(\ast\)
公式を導出するまでのに多くの時間と労力を要するのなら,その結果を覚えることも確かに必要です.しかし,そうでないのなら,必要に応じてその場で作ってしまえばいいと割り切ってしまうのもひとつの姿勢です.
結果を覚えるのではなく,導出できるようにしておけば,万が一忘れてもすぐに再現できる.忘れてもいいやと開き直れる.導出過程自体が解法の糸口になることもある.他の公式との共通点が見えきて機会が深まことだって珍しくない.いいことづくめ.
公式を結果だけ覚えろ,あるいは覚えるしかないなどと言われたら相手が誰であれ警戒しましょう.一旦立ち止まり,本当に覚える必要のある式なのか?記憶に頼らずにかわす方法はないか?を自分自身の頭で考える癖を持ちしましょう.自分ひとりで判断できなければ,友人をはじめいろいろな人に意見を求めましょう.数学においても「セカンドオピニオン」は重要です.




