\(A,B\)が位相空間\(S\)の閉集合で,\(A \cup B,A \cap B\)がともに連結ならば,\(A,B\)はいずれも連結であることを示せ.
これで半日潰した(´;ω;`)
証明
\(A\)が連結でないか,または\(B\)が連結ではないとする.ここでは\(A\)が連結ではないと仮定する.すなわち,\[\exists A_1,A_2\in\mathfrak{A}_A[A=A_1\cup A_2,A_1\cap A_2=\phi,A_1\neq \phi,A_2 \neq \phi]\]ただし\(\mathfrak{A}_A\)は相対位相\(\mathfrak{A}_A=\{A^{\prime}\cap A|A^{\prime}\in \mathfrak{A}\}\),\(\mathfrak{A}\)は\(S\)の位相.
\(A\cap B\)が連結であることから,\begin{align*}&\lnot(\exists A_1^{\prime},A_2^{\prime}\in \mathfrak{A}_{A\cap B}[A\cap B=A_1^{\prime}\cup A_2^{\prime},A_1^{\prime}\cap A_2^{\prime}=\phi,A_1^{\prime}\neq \phi,A_2^{\prime}\neq\phi])\\ \Longleftrightarrow~&\forall A_1^{\prime},A_2^{\prime}\in \mathfrak{A}_{A\cap B}\\&[A\cap B\neq A_1^{\prime}\cup A_2^{\prime}\text{(あ)}\lor A_1^{\prime}\cap A_2^{\prime}\neq \phi \text{(い)}\lor A_1^{\prime}=\phi \lor A_2^{\prime}=\phi\text{(う)}]\end{align*}ただし\(\mathfrak{A}_{A \cap B}=\{A^{\prime}\cap(A\cap B)|A^{\prime}\in \mathfrak{A}\}\).ここで,
\begin{cases}
A\cap B=(A_1 \cup A_2)\cap B =(A_1 \cap B)\cup (A_2 \cap B)\\
(A_1 \cap B) \cup (A_2 \cap B) =A_1 \cap A_2 \cap B)=\phi\\
A_1 \cap B = (A^{\prime} \cap A)\cap B=A^{\prime} \cap (A\cap B)~(A^{\prime}\in\mathfrak{A})したがってA_1\cap B\in \mathfrak{A}_{A\cap B}\\
A_2 \cap B = (A^{\prime} \cap A)\cap B=A^{\prime} \cap (A\cap B)~(A^{\prime}\in\mathfrak{A})したがってA_2\cap B\in \mathfrak{A}_{A\cap B}
\end{cases}
であるから,\(A_1^{\prime}=A_1 \cap B,A_2^{\prime}=A_2 \cap B\)とすれば,(あ)(い)は成り立たない.したがって,(う)\(A_1\cap B =\phi \lor A_2\cap B=\phi\)でなくてはならない.たとえば\(A_1\cap B=\phi\)とする.このとき,
\begin{cases}
A\cup B=(A_1 \cup A_2)\cup B =A_1 \cup (A_2 \cup B)\\
A_1\cap (A_2 \cup B)=(A_1\cap A_2) \cup(A_1\cap B)=\phi \cup \phi =\phi\\
A_1\neq \phi,A_2 \cup B \neq \phi
\end{cases}
あとは\(A_1, A_2 \cup B\in \mathfrak{A}_{A\cup B}\)であることが示せれば,\(A\cup B\)が連結であることと矛盾し,\(A_1\cap B\neq\phi\)となる.\(A_2\cap B\neq\phi\)も同様にして示せる.すると\(A\cap B\)が連結であることと矛盾し,証明が完了する.
\(A_1\in \mathfrak{A}_{A\cup B}\)であること:\(A_1 \cap B =\phi\)に注意して
\begin{align*}
A_1=&A_1 \cup (A_1 \cap B)=A_1 \cap (A_1 \cup B)=(A^{\prime}\cap A) \cap ((A^{\prime}\cap A) \cup B))\\
=&(A^{\prime}\cap A) \cap ((A^{\prime}\cup B)\cap (A\cup B))=((A^{\prime}\cap A) \cap (A^{\prime}\cup B))\cap (A\cup B)
\end{align*}\(A,B,A^{\prime}\in \mathfrak{A}\)だから,\((A^{\prime}\cap A) \cap (A^{\prime}\cup B)\in \mathfrak{A}\).したがって\(A_1\in\mathfrak{A}_{A\cup B}\)
\(A_2 \cup B \in \mathfrak{A}_{A\cup B}\)であること:\(A_2 \cup B=(A^{\prime}\cap A) \cup B=(A^{\prime}\cup B)\cap (A\cup B) \).\(A^{\prime},B\in \mathfrak{A}\)だから\(A^{\prime}\cup B \in \mathfrak{A}\).よって\(A_2\cup B\in\mathfrak{A}_{A\cup B}\)
証明終
疲れた。
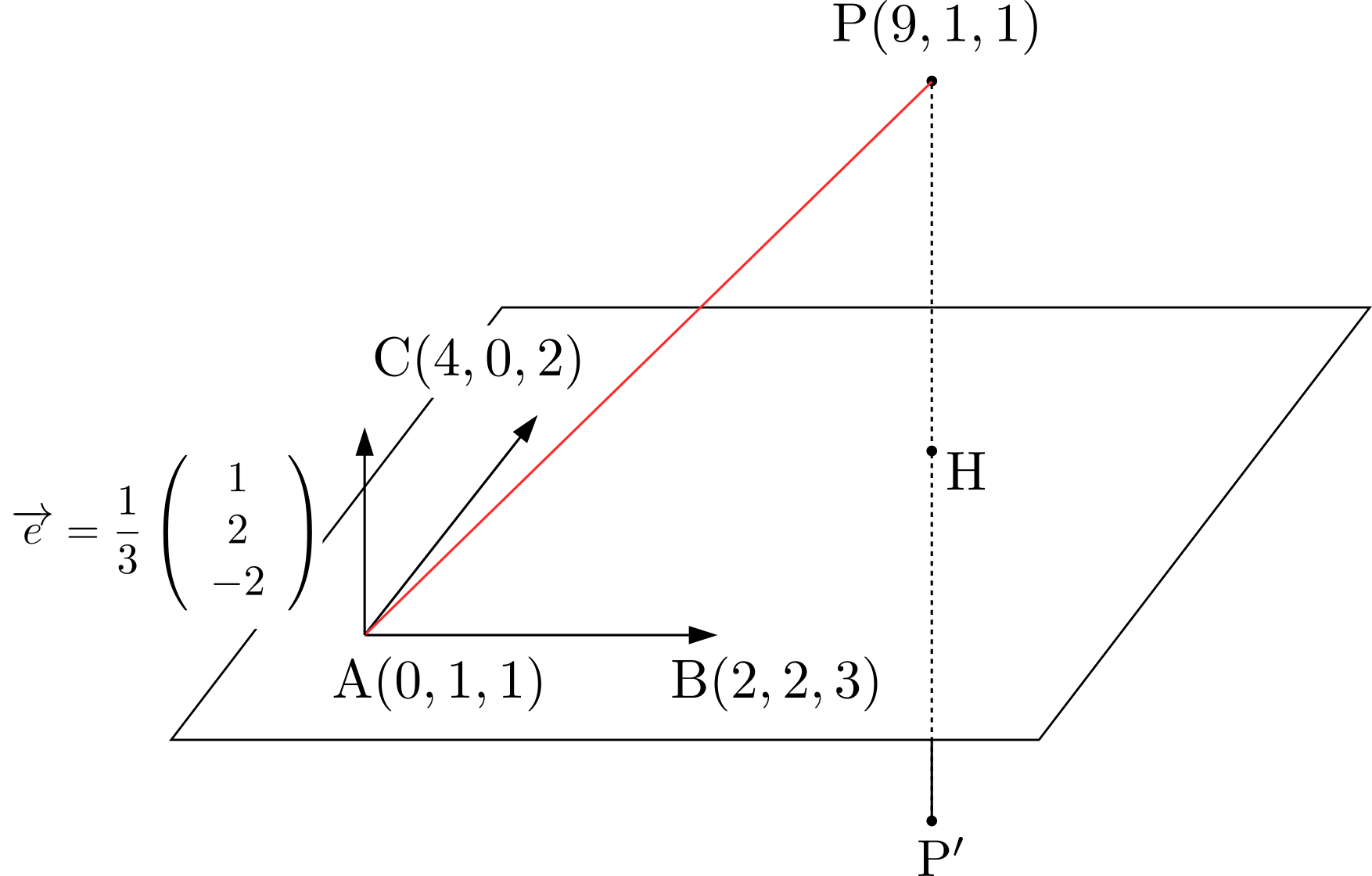
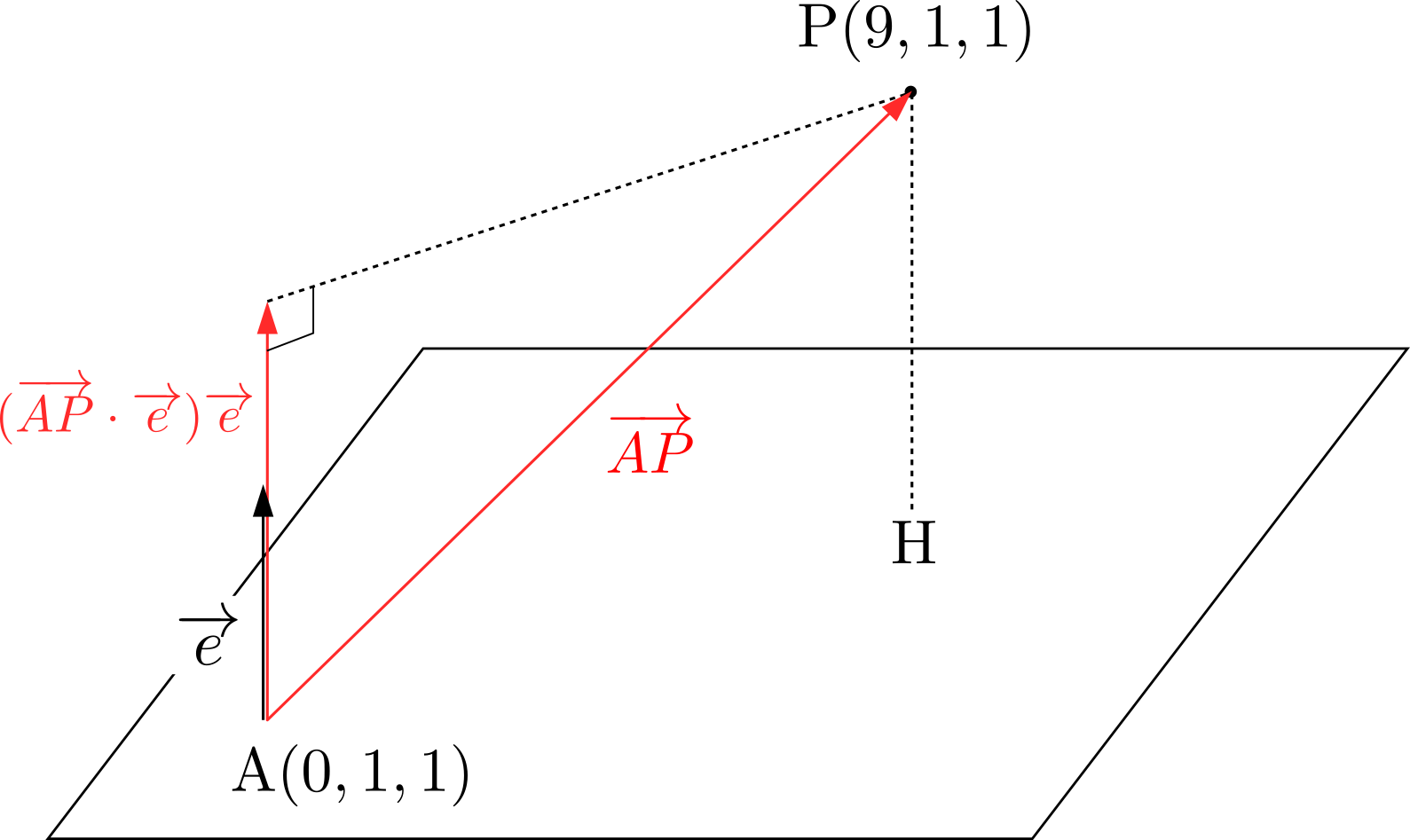
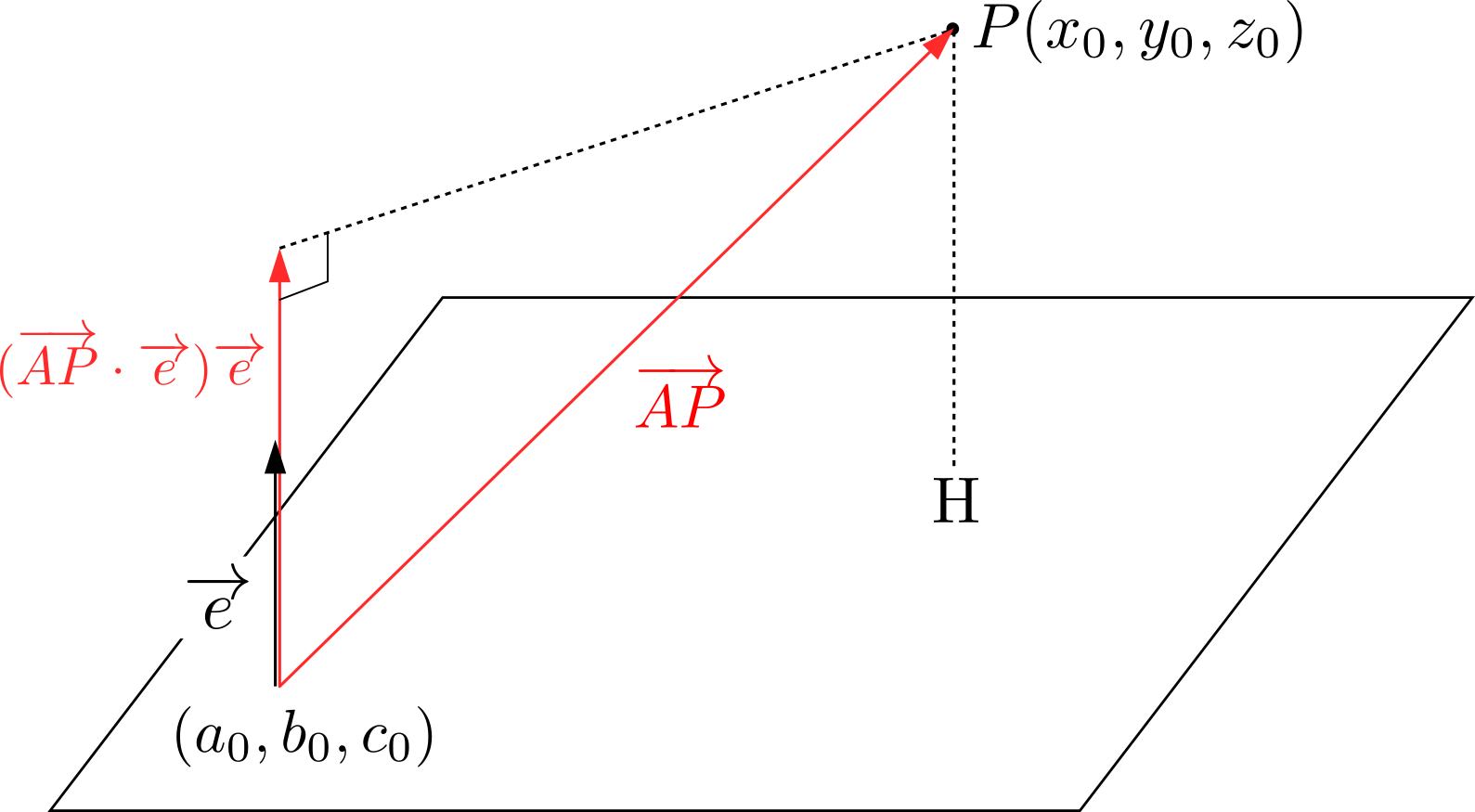 \((a_0,b_0,c_0)\)を平面上の点とする.点\(P\)から平面へおろした足を\(H\)とおけば,線分\(PH\)の長さは正射影ベクトル\((\overrightarrow{AP}\cdot \overrightarrow{e})\overrightarrow{e}\)の大きさと等しい.したがって
\((a_0,b_0,c_0)\)を平面上の点とする.点\(P\)から平面へおろした足を\(H\)とおけば,線分\(PH\)の長さは正射影ベクトル\((\overrightarrow{AP}\cdot \overrightarrow{e})\overrightarrow{e}\)の大きさと等しい.したがって

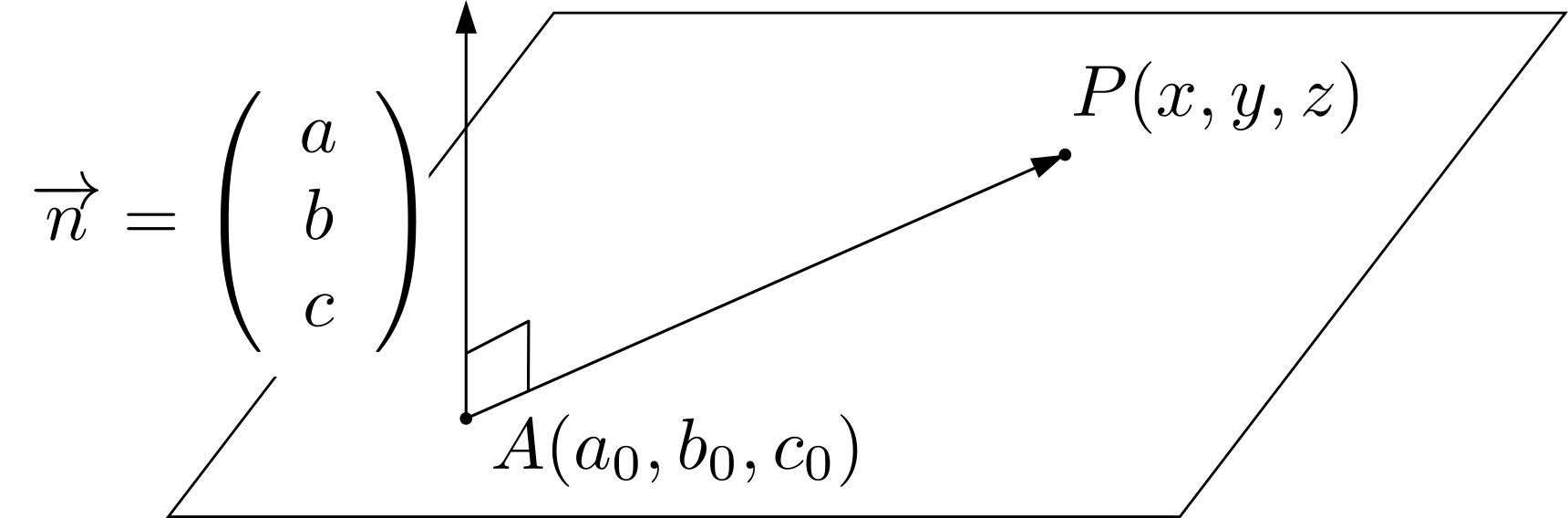 ここでは,平面はその平面の垂直方向とその平面が通る1点が定まれば決定することに着目します。平面の法線ベクトルを\(\overrightarrow{n}=(a,b,c)\),平面が通る1点の座標を\(A(a_0,b_0,c_0)\),平面上の任意の点を\(P(x,y,z)\)とおくことにします。\begin{align*}
ここでは,平面はその平面の垂直方向とその平面が通る1点が定まれば決定することに着目します。平面の法線ベクトルを\(\overrightarrow{n}=(a,b,c)\),平面が通る1点の座標を\(A(a_0,b_0,c_0)\),平面上の任意の点を\(P(x,y,z)\)とおくことにします。\begin{align*}
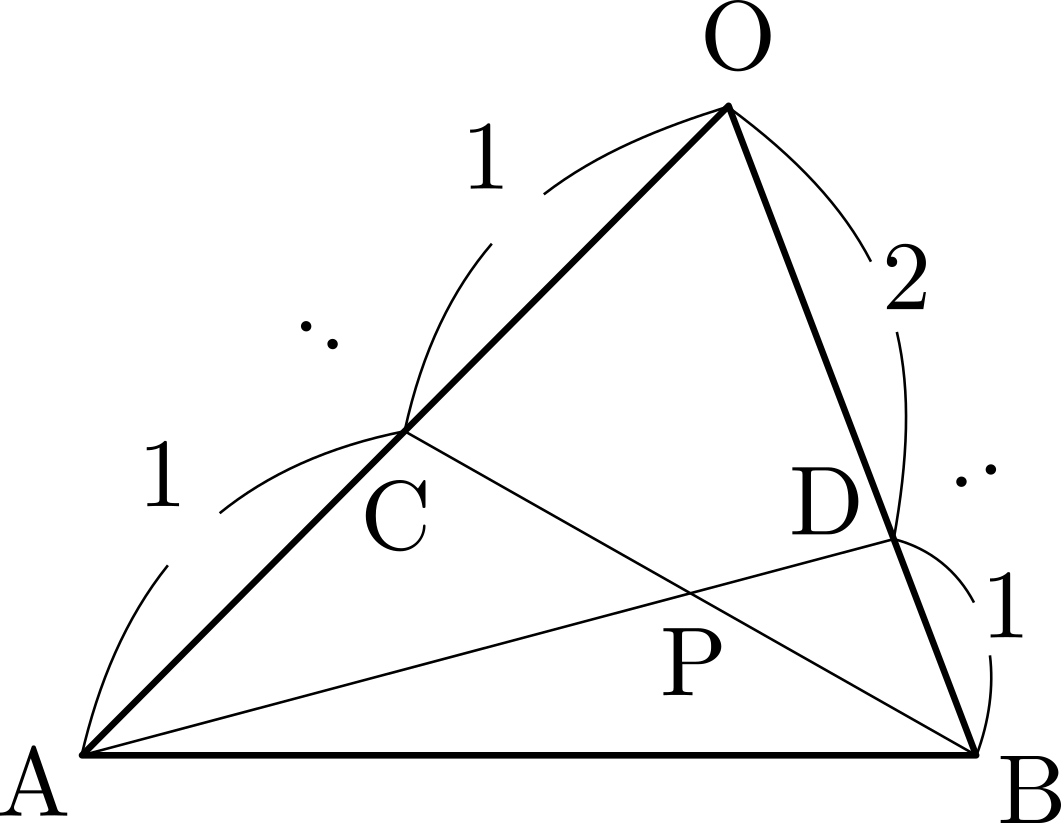
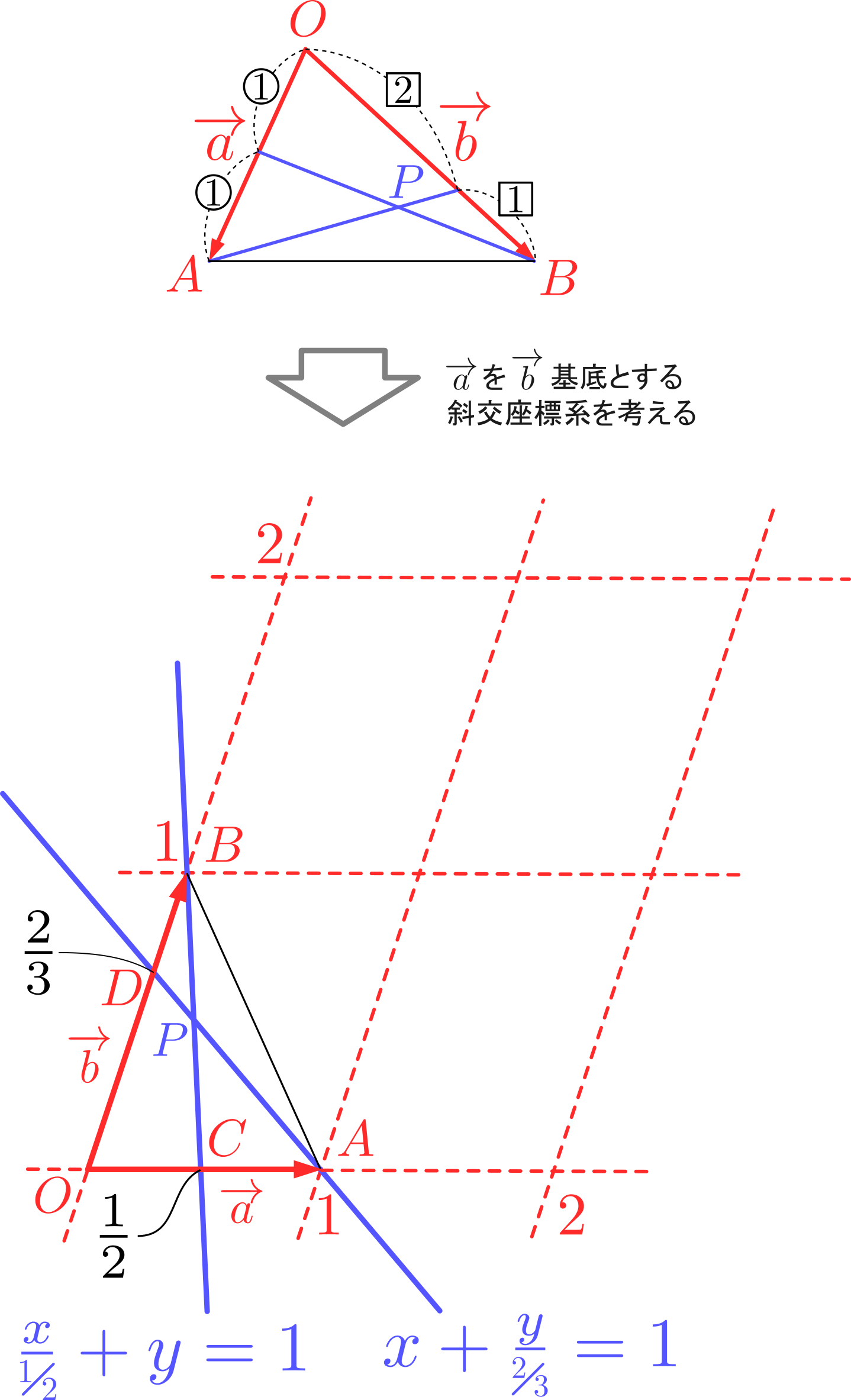
 ここで,
ここで,