頂点と辺(直線でなくともOK)を結んだ図形をグラフと呼びます.
ここで,
・すべての辺を1回だけ通り,
・出発点に戻る
道が存在する(すなわち一筆書きができる)グラフ
つまり一筆書きして出発点に戻ってこられるグラフをオイラーグラフと呼びます.
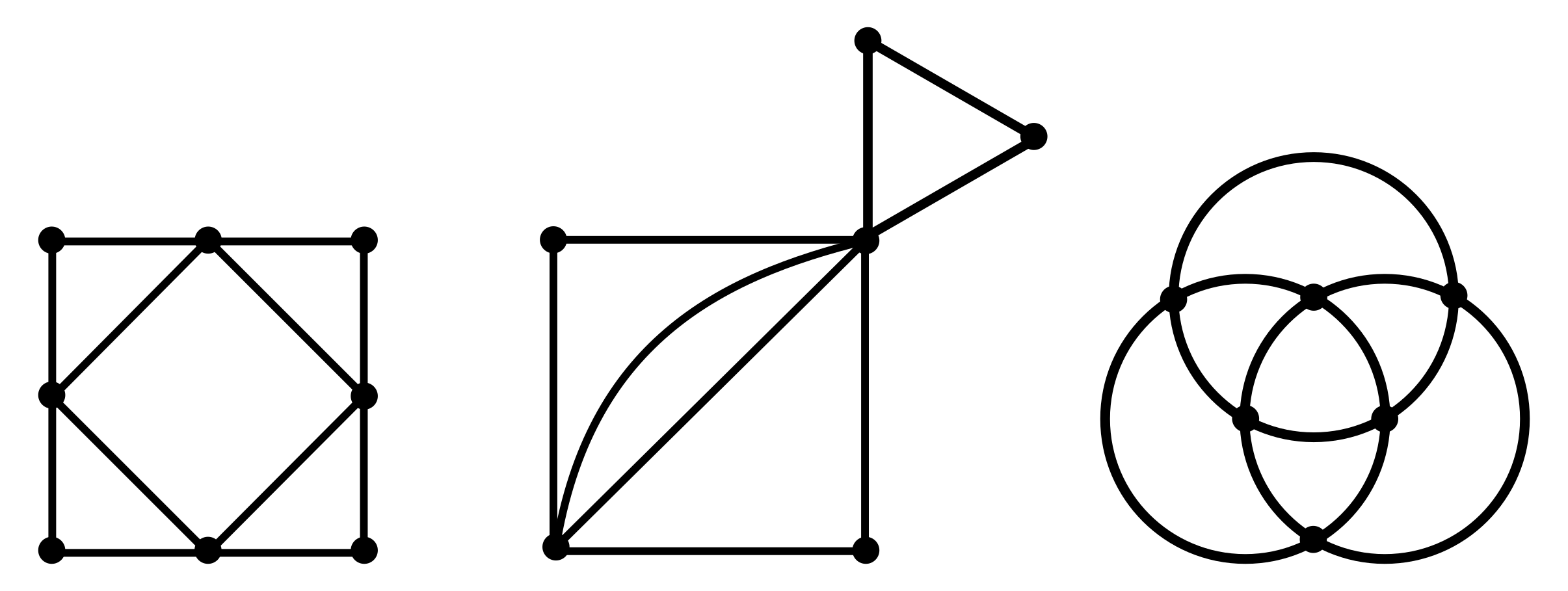
このオイラーグラフに関して,次の定理があります(頂点に集まる辺の本数を次数とよび,次数が偶数であるような頂点を偶点,次数が奇数であるような頂点を奇点と呼びます).
\[\text{オイラーグラフ}\Longleftrightarrow{頂点がすべて偶点}\]
この定理より,例えば上の三つのグラフの頂点はどれも偶点だけなのでいずれもオイラーグラフであることがわかります.つまり一筆書きできます!下の証明は,一筆書きを見つけるための一般論にもなっています.
証明
(\(\Longrightarrow\)の証明)
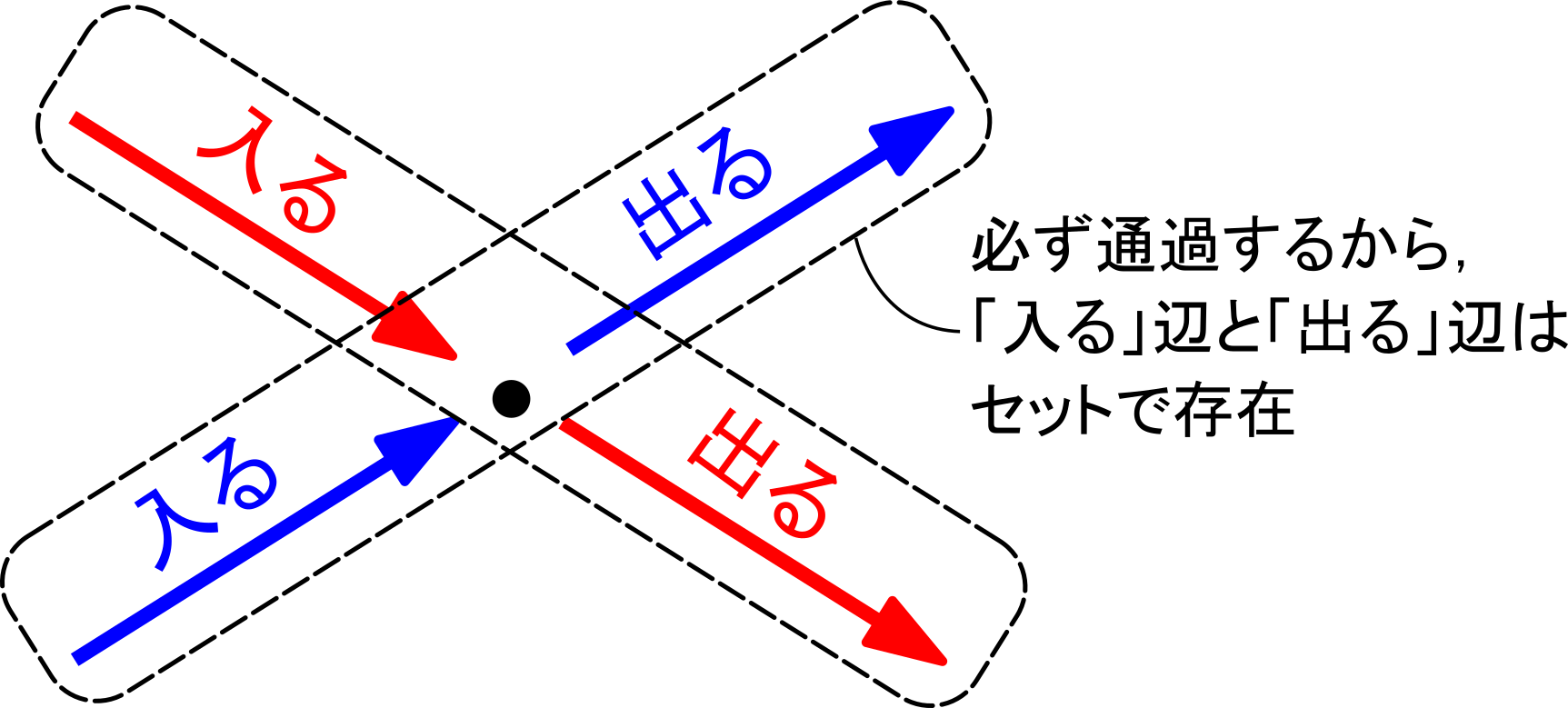 グラフがオイラーグラフであるとする.オイラーグラフとはいわば「一筆書きして出発点に戻ってこられる」ようなグラフであるから,各頂点において,その頂点で袋小路になることなく通過できることになる.これはその頂点に「入る」辺があれば必ず「出ていく」辺もセットで存在することを意味する(2本がセットとなる).したがって各頂点における次数は2の倍数となる.ゆえに,すべての頂点は偶点であるといえる.
グラフがオイラーグラフであるとする.オイラーグラフとはいわば「一筆書きして出発点に戻ってこられる」ようなグラフであるから,各頂点において,その頂点で袋小路になることなく通過できることになる.これはその頂点に「入る」辺があれば必ず「出ていく」辺もセットで存在することを意味する(2本がセットとなる).したがって各頂点における次数は2の倍数となる.ゆえに,すべての頂点は偶点であるといえる.
(\(\Longleftarrow\)の証明)
すべての頂点が偶点となるグラフを考える.辺の数が1のとき,すべての頂点は奇点となるから考える必要はない.したがって辺の本数を\(n\)として\(n\geq2\)で考える.

\(n\)に関する帰納法で証明する.
\(n<k\)のとき,与えらえた命題が正しいと仮定,すなわち\[\text{\(k-1\)個以下の頂点すべてが偶点\(~\Longrightarrow~\)オイラーグラフ}\]であると仮定する.この仮定のもとで,
\[\text{\(k\)個の頂点すべてが偶点\(~\Longrightarrow~\)オイラーグラフ}\]が示せればよい.
まとめると,今手元にある仮定は,
\[
\begin{cases}
\text{\(k-1\)個以下の頂点すべてが偶点\(~\Longrightarrow~\)オイラーグラフ}\quad \cdots (1)\\
\text{\(k\)個の頂点すべてが偶点}\quad \cdots (2)
\end{cases}
\]
であり,この下で,\(k\)個の頂点をもつグラフがオイラーグラフであることが示せればよい.
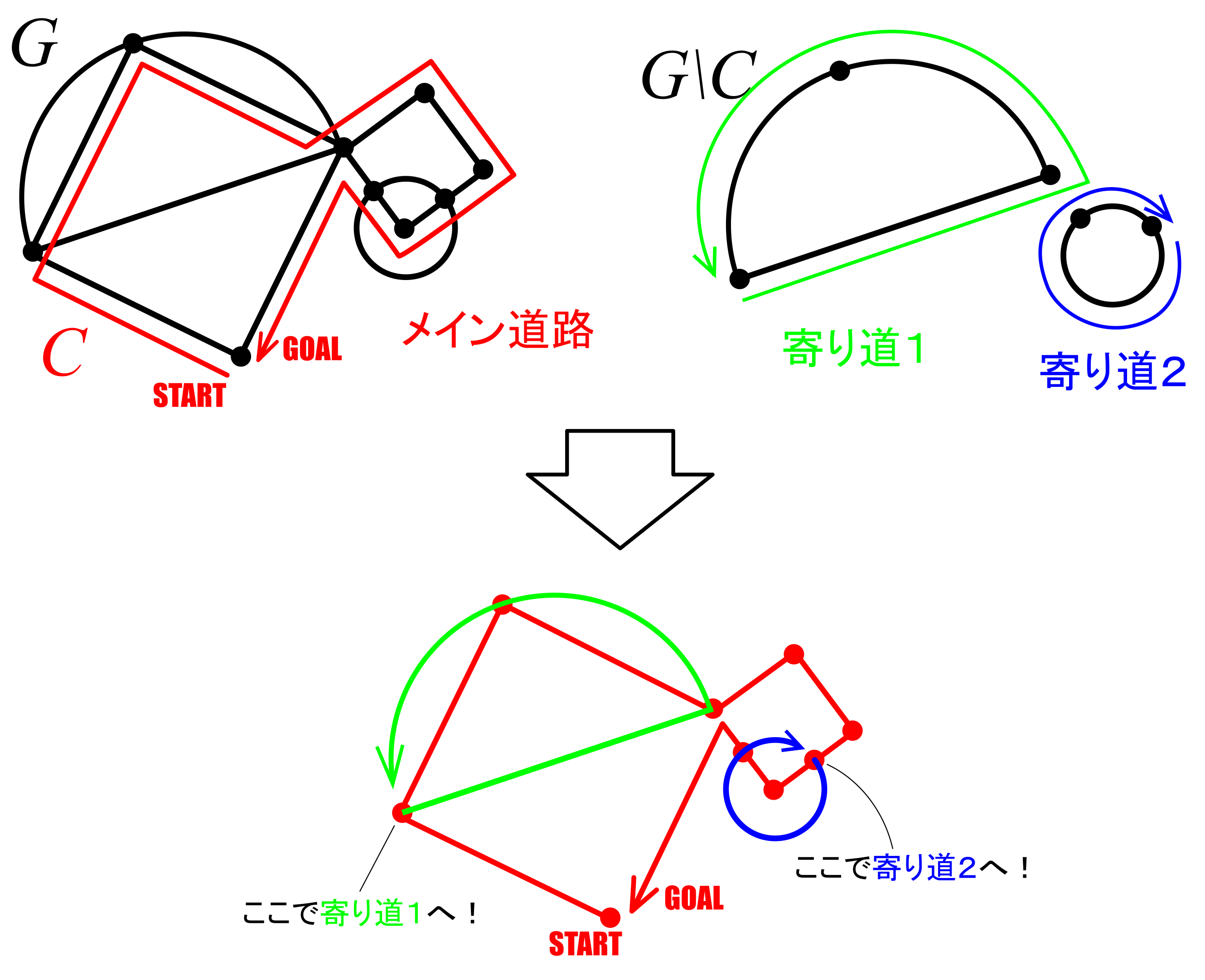
今,仮定(2)よりグラフの\(k\)個の頂点はすべて偶点である.このグラフ(\(G\)とおく)は閉路\(C\)をもつ.この閉路\(C\)を抜き出す(下図参照).グラフ\(C\)を抜き出したあとのグラフを\(G\backslash C\)とおく.
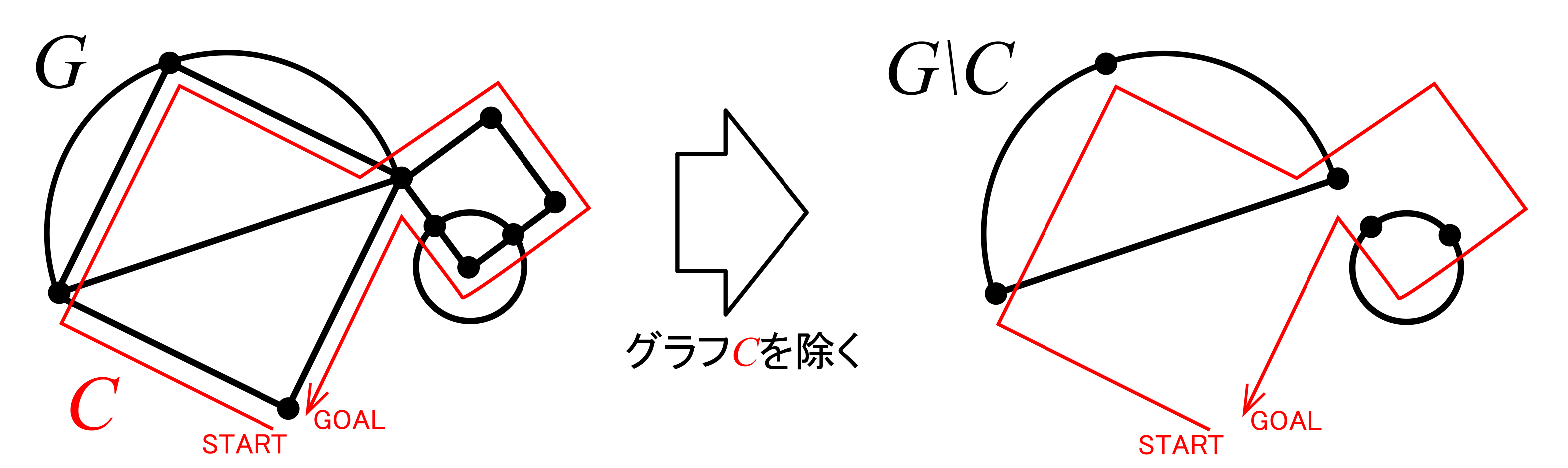
閉路\(C\)を抜き出しても,各頂点は偶点のままであることに注意する(なぜなら\(C\)を抜き出したあと,頂点から次数が\(2\)の倍数だけ減ることになるが,もともと偶点なので,\(\text{偶数}-2\text{の倍数}=\text{偶数}\)より,残った頂点もやっぱり偶点となるから.下図参照).
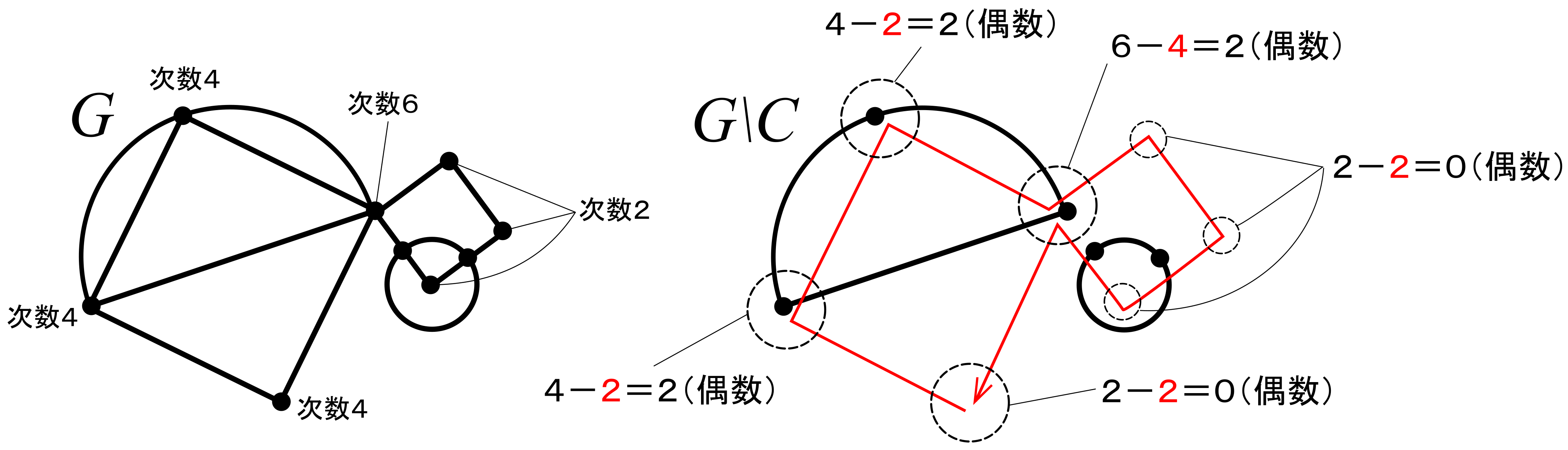
残ったグラフ\(G\backslash C\)の頂点はすべて偶点であるから,仮定(1)より,\(G\backslash C\)はすべてオイラーグラフといえる.
グラフ\(C\)を辿る過程で,残ったグラフ\(G\backslash C\)(オイラーグラフ)を寄り道しながらたどれば一筆書きができる(下図参照).すなわち\(G\)はオイラーグラフである.
\(n=2\)で各頂点が偶点であるようなグラフがオイラーグラフであることは明らか.(証明終)
この証明から分かるように,「一筆書きの見つけ方」は以下のようになります:
① まず何でもいいから閉路(ア)をみつけ,その閉路(ア)を取り除く.
② 取り除いたあとのグラフから,一筆書きの経路(イ)(ウ)を見つける.
③ あとは(ア)を進む途中で(イ)(ウ)に寄り道して出発点に戻る.
②の段階で一筆書き(イ)(ウ)が見つけづらい場合は,そのグラフのもとで再び①②の操作を行えばOK.
これで理論上はどんなオイラーグラフも一筆書きの経路が見つかります.

