上の放物線と直線で囲まれる部分の面積\(S\)は,いずれの場合も\[S = \frac{|a|(\beta-\alpha)^3}{6}\]で表される.
証明
\(a>0\)の場合と\(a<0\)の場合とで場合を分けて考える.
(\(a>0\)の場合)
被積分関数\(g(x)-f(x)\)がどんな関数になるかを考える.これは,
-
-
- \(2\)次式で,
- 次数が一番大きい項の係数は\(-a\)で,
- 交点が\(\alpha,\beta\)すなわち\(g(x)-f(x)=0\)を解いて得られる\(2\)つの解が\(\alpha,\beta\)である
-
ことに着目すると,\[f(x)-g(x)=-a(x-\alpha)(x-\beta)\]とかける.したがって求める部分の面積は
\begin{align*}
&\displaystyle \int_{\alpha}^{\beta} -a(x-\alpha)(x-\beta) dx \\
=~&\displaystyle a\int_{\alpha}^{\beta} -(x-\alpha)(x-\beta) dx\\
=~&\frac{a(\beta-\alpha)^3}{6}\tag{1}\\
=~&\frac{|a|(\beta-\alpha)^3}{6}
\end{align*}
(\(a<0\)の場合)
被積分関数は\(f(x)-g(x)\)であるから,上と同様に考え,\[f(x)-g(x) = a(x-\alpha)(x-\beta)\]したがって求める部分の面積は
\begin{align*}
&\displaystyle \int_{\alpha}^{\beta} a(x-\alpha)(x-\beta) dx \\
=~&\displaystyle -a\int_{\alpha}^{\beta} -(x-\alpha)(x-\beta) dx\\
=~&\frac{-a(\beta-\alpha)^3}{6}\tag{1}\\
=~&\frac{|a|(\beta-\alpha)^3}{6}
\end{align*}
以上により,いずれの場合も面積\(S\)は\[\frac{|a|(\beta-\alpha)^3}{6}\]で表されることになる.
証明終
大事なポイントは被積分関数\(g(x)-f(x),~f(x)-g(x)\)を書くところです。これを実際に書き出して項を整理して因数分解を考え…などと愚直に計算するのは間違いではありませんがあまりよい手とは言えません。上で見たように,\(g(x)-f(x),~f(x)-g(x)\)を特徴付ける(3つの)要素さえ分かってしまえば即答できるわけですから。また,\((1)\)は定積分の有名公式によります。あの公式は具体的にはこんなシチュエーションで役に立つ,ということです。
結局,交点\(\alpha,\beta\)と係数\(a\)という情報だけで面積が求まってしまうということになります.
模試以上の問題ならばこの公式は(そのレベルの問題だとこれは単なる‘途中計算’に過ぎませんから)証明抜きで使っても問題ないと思われます.しかし学校のテストなどは立式~定積分の計算を問う意図もあるかと思うのでもしかしたら嫌がられるかもしれません.とはいえ,学校のテスト(=教科書の例題・練習題)だとぐちゃぐちゃ計算させようとする問題も多く,そんなのに付き合わせられるのもうざったらしいので,この証明を解答欄の脇にでもササっと記述して以降の問題を公式で済ませてしまうというのもひとつの手だと思います(証明する必要があるかどうかは,作問する先生に事前に確認しておくとよいでしょう).
他にも覚えておくと便利な公式があります。随時更新していきます.


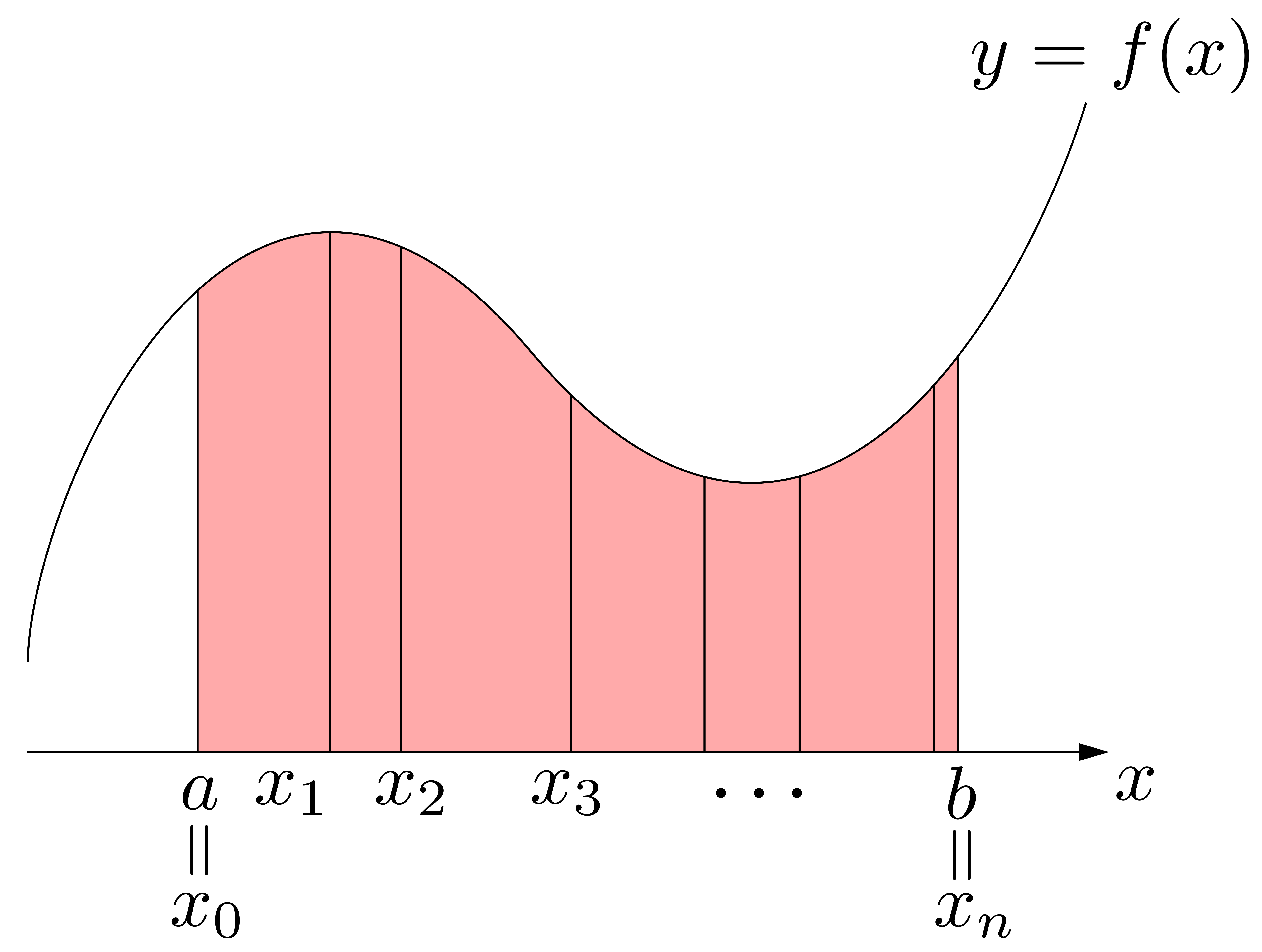
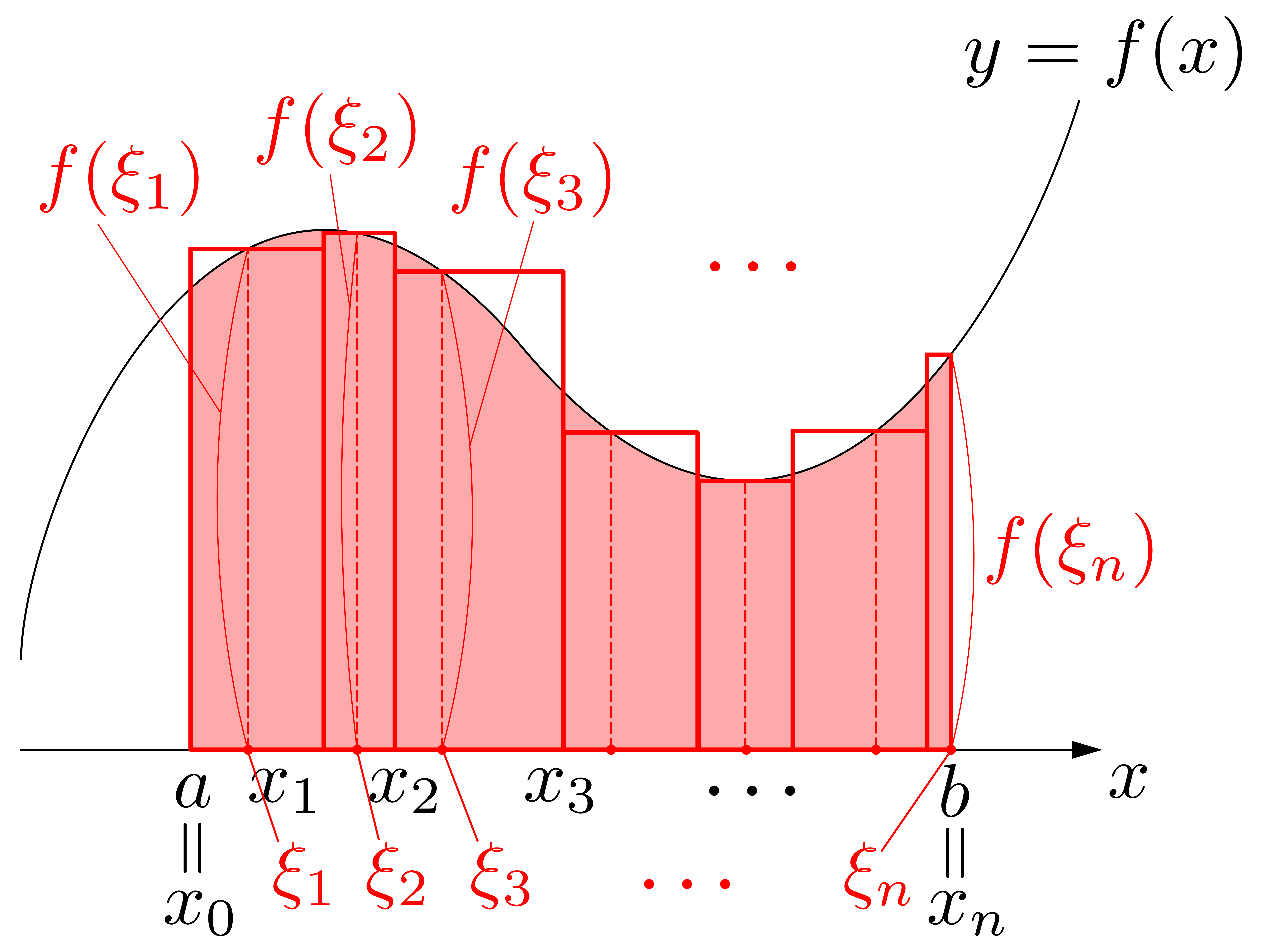

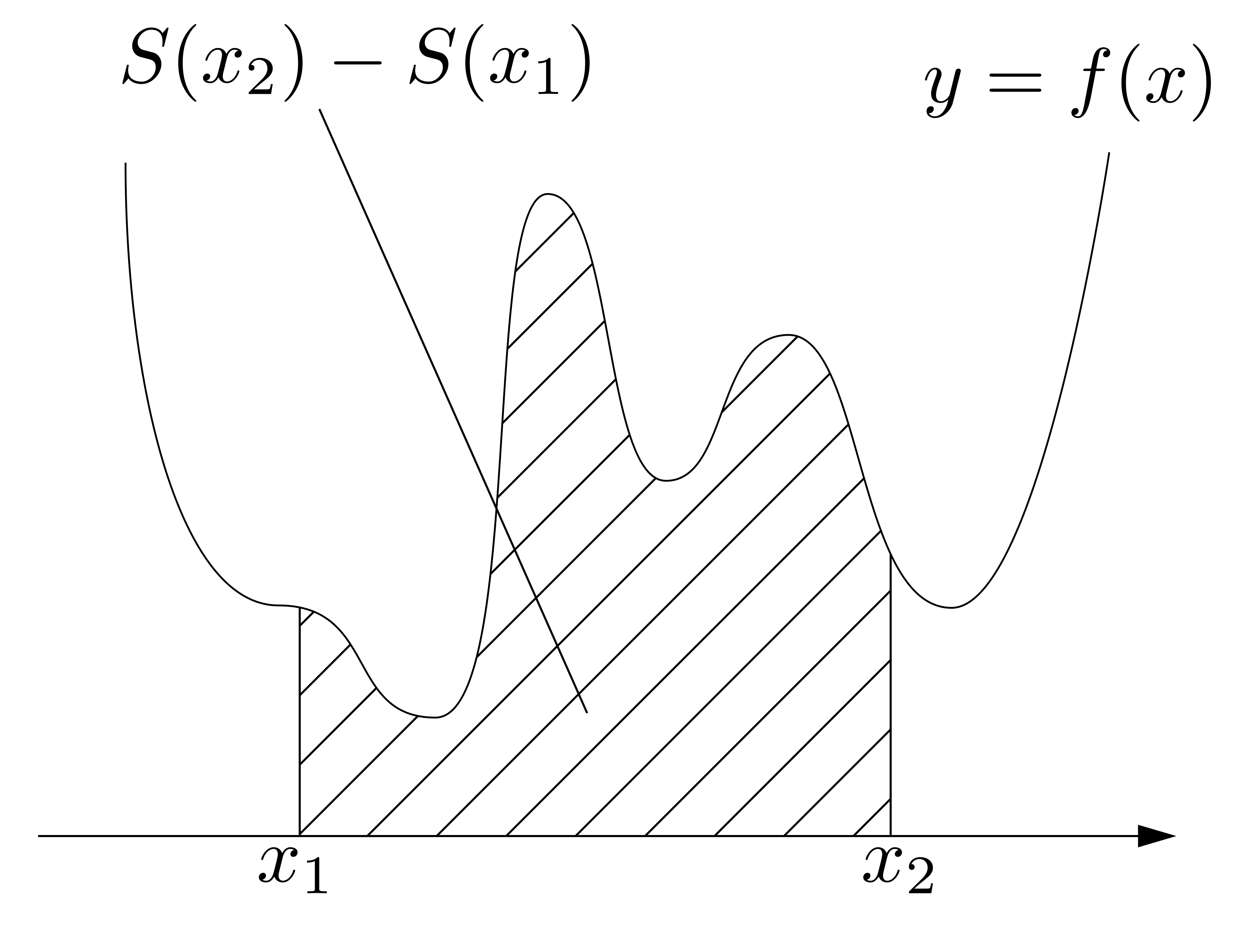
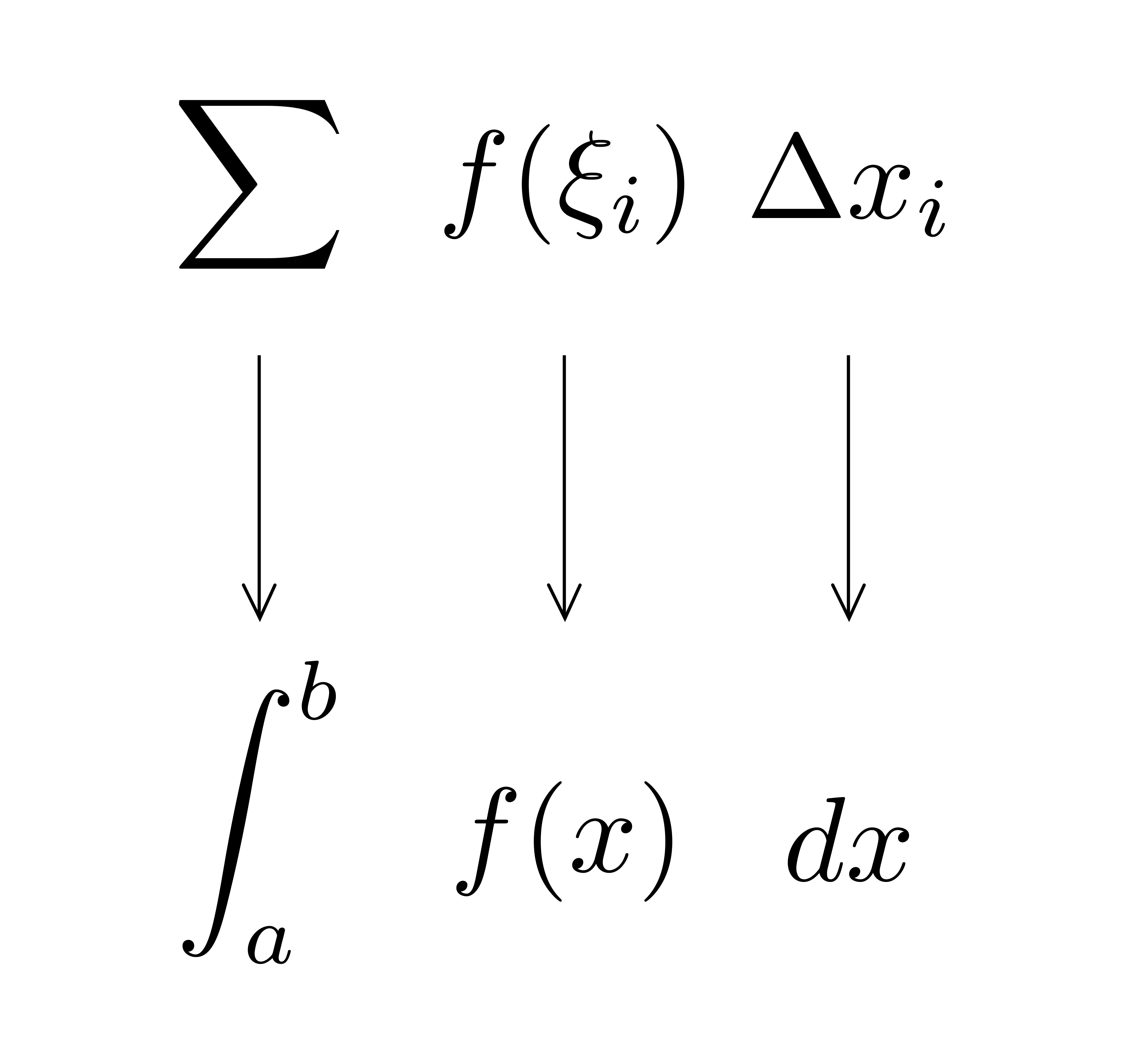 以上を見ると,\(\displaystyle \int^b_a f(x)dx\)の\(\displaystyle \int\)や\(dx\)の「イメージ」が見えてきます.右図に示すように,\(\displaystyle \sum\)が\(\displaystyle \int\)に,\(\Delta x_i\)が\(dx\)と対応しているわけです.
以上を見ると,\(\displaystyle \int^b_a f(x)dx\)の\(\displaystyle \int\)や\(dx\)の「イメージ」が見えてきます.右図に示すように,\(\displaystyle \sum\)が\(\displaystyle \int\)に,\(\Delta x_i\)が\(dx\)と対応しているわけです.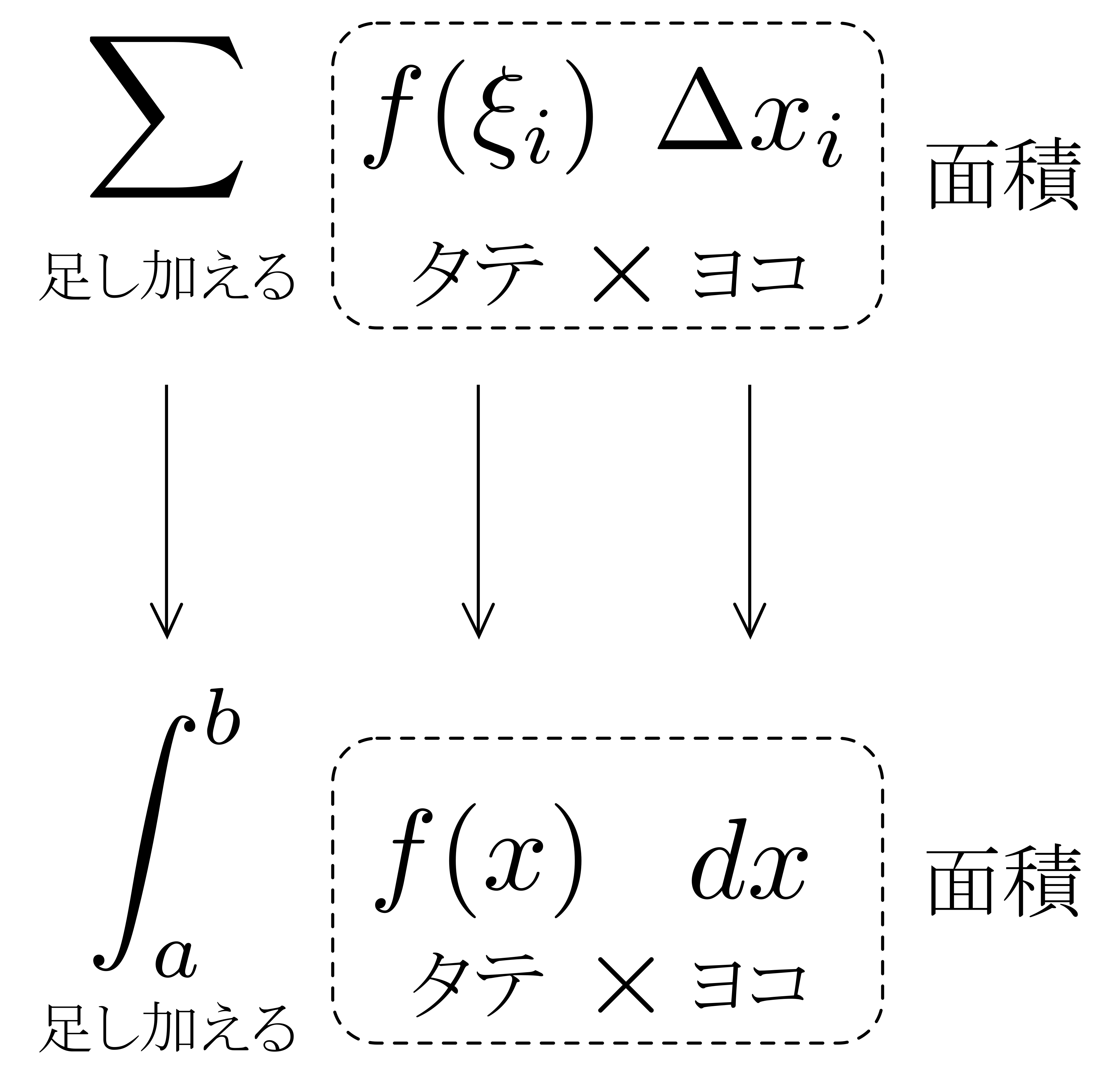 以上を踏まえて\(\displaystyle \int^b_a f(x)dx\)を眺めると,これは「微小面積\(f(x)\times dx\)を\(\displaystyle \int\)したもの(連続的に足し加えたもの)」と読み取れることが分かります!
以上を踏まえて\(\displaystyle \int^b_a f(x)dx\)を眺めると,これは「微小面積\(f(x)\times dx\)を\(\displaystyle \int\)したもの(連続的に足し加えたもの)」と読み取れることが分かります!