この問題を２通りの解法で解いてみます．
（解法１）
定義域\(0 \leq x \leq 2\)に属する\(x\)に対応する\(y\)を調べます．
\(x=0\)に対応する\(y\)は？\(y=0+1=1\)．
\(\hspace{35mm}\vdots\)
\(x=1\)に対応する\(y\)は？\(y=1+1=2\)．
\(\hspace{35mm}\vdots\)
\(x=2\)に対応する\(y\)は？\(y=2+1=3\)．
と調べていけば，\(1\leq y \leq 3\)と求まります．この頭の動きを図示すると，
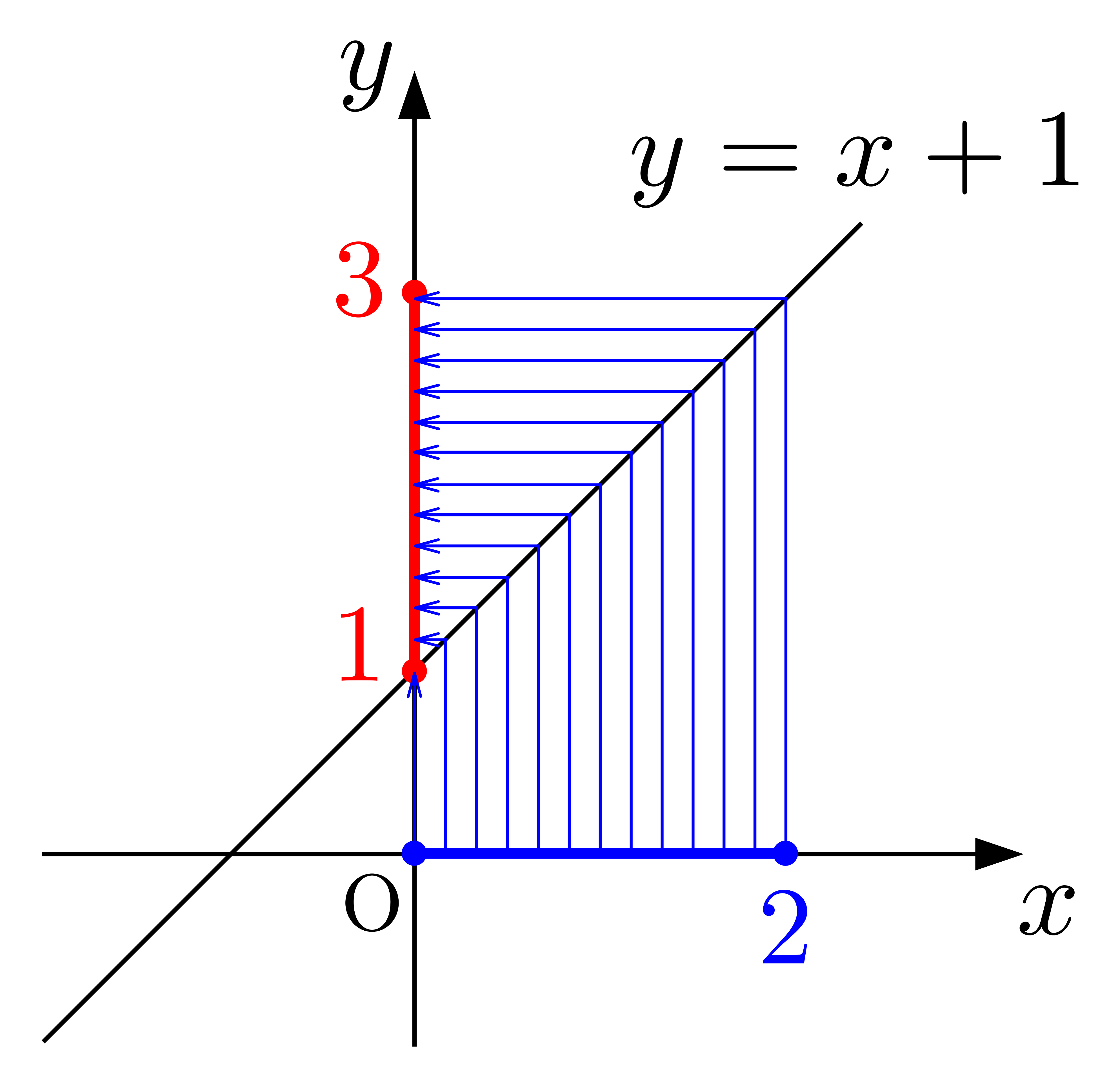
のようになります．矢印の向きに注意してください．重要なのは次の（解法２）の考え方です．
（解法２）
頭の中で何でもいいから実数を思い浮かべてください．
ここでは例えば，
\[2\]
と頭に思い浮かべたとしましょう．
次に，その\(2\)に対応する\(x\)の値を求めてください．
\[2=x+1~\Longleftrightarrow~x=1\]
よって，\(1\)と分かります．
では，例えば\(4\)ならどうでしょう？\(3\)に対応する\(x\)を調べてみます．
\[4=x+1~\Longleftrightarrow~x=3\]
よって，\(3\)と分かります．
さて，今二つの例を挙げましたが，この二つの例の違いは何でしょうか？それは，
\(2\)に対応する\(x\)は，定義域にある（存在する）．
\(4\)に対応する\(x\)は，定義域にはない（存在しない）．
ということです．図示すると，
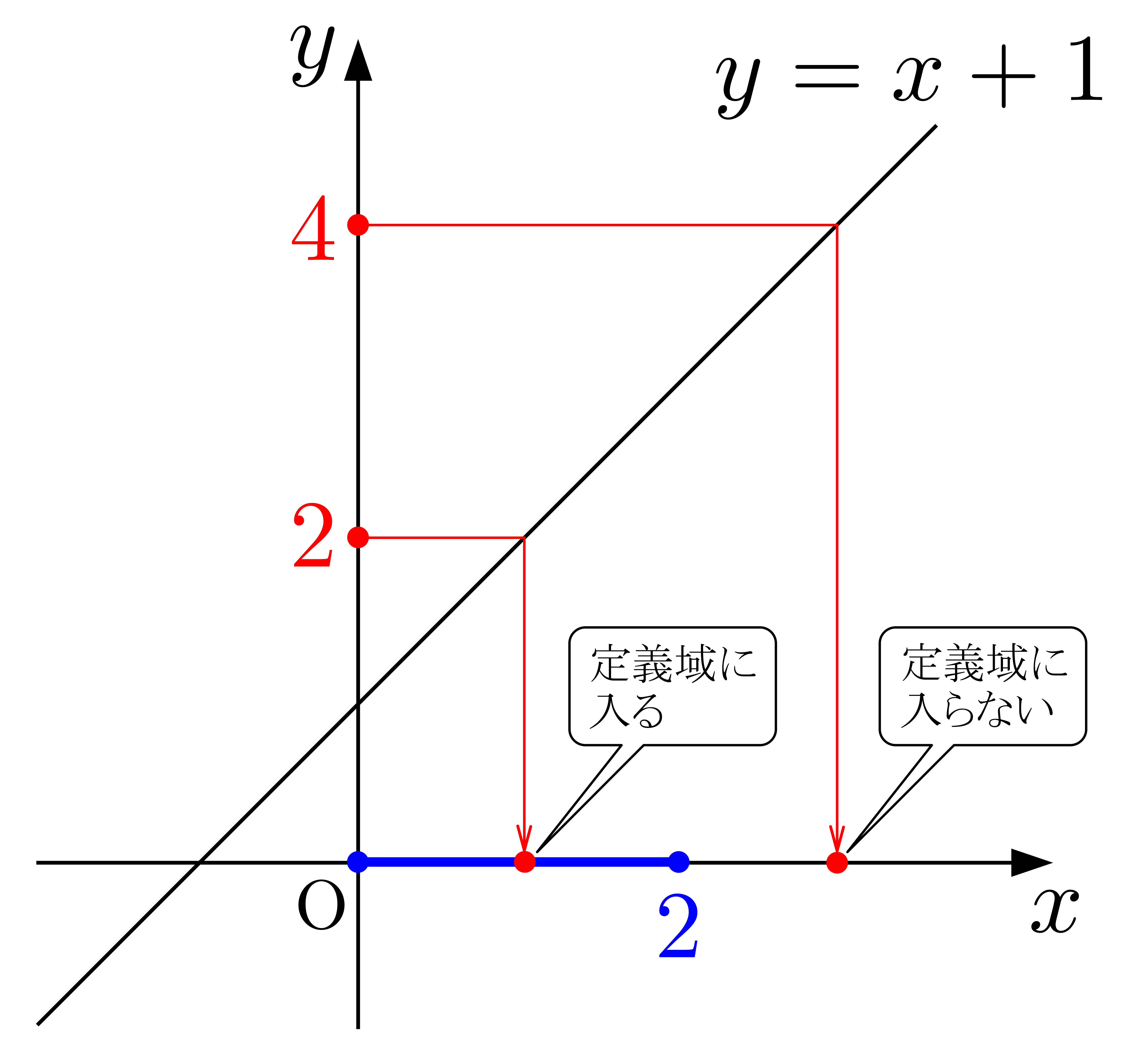
これを，それぞれ次のように解釈します．
「\(2\)に対応する\(x\)が定義域に存在する\(~\Longrightarrow~\)\(2\)は求める値域（の点の１つ）」
「\(3\)に対応する\(x\)が定義域に存在しない\(~\Longrightarrow~\)\(3\)は値域（の点の１つ）ではない」
また，「値域」「定義域」という言葉の定義から逆も成り立つのは明らかですから，結局，
「\(2\)に対応する\(x\)が定義域内に存在する\(~\Longleftrightarrow~\)\(2\)は求める値域（の点の１つ）」
「\(3\)に対応する\(x\)が定義域内に存在しない\(~\Longleftrightarrow~\)\(3\)は値域（の点の１つ）ではない」
と言えます．したがって，「\(y=2\)は値域上の点だが\(y=3\)は値域上の点ではない」と分かります．
以上の考え方（頭に何か数字を思い浮かべ，その数に対応する\(x\)を調べ，それが定義域内にあるかどうかを調べる）を用いて他の点についても調べてみましょう．色々な点を頭に思い浮かべて…．\(4,~1,~1.5,~0.5,~5,~\frac{7}{2},~3,~\frac{5}{2},~-\frac{1}{2},~-1\cdots\)
\(4\)に対応する\(x\)は？
\(3\)です．\(3\)は定義域の点ではないので，値域の点ではありません．すなわち，
「\(4\)に対応する\(x\)が定義域に存在しない\(~\Longleftrightarrow~\)\(4\)は求める値域（の点の１つ）ではない」
\(1\)に対応する\(x\)は？
\(0\)です．\(0\)は定義域の点なので，値域の点のひとつです．すなわち，
「\(1\)に対応する\(x\)が定義域に存在する\(~\Longleftrightarrow~\)\(1\)は求める値域（の点の１つ）である」
\(\frac{3}{2}\)に対応する\(x\)は？
\(\frac{1}{2}\)です．\(\frac{1}{2}\)は定義域の点なので，値域の点のひとつです．すなわち，
「\(\frac{3}{2}\)に対応する\(x\)が定義域に存在する\(~\Longleftrightarrow~\)\(\frac{3}{2}\)は求める値域（の点の１つ）である」
\(\frac{1}{2}\)に対応する\(x\)は？
\(-\frac{1}{2}\)です．\(-\frac{1}{2}\)は定義域の点ではないので，値域の点ではありません．すなわち，
「\(\frac{1}{2}\)に対応する\(x\)が定義域に存在しない\(~\Longleftrightarrow~\)\(\frac{1}{2}\)は求める値域（の点の１つ）ではない」
\(\hspace{80mm}\vdots\)
と調べていけば，徐々に欲しい値域らしきものが求まっていくことが想像できると思います．
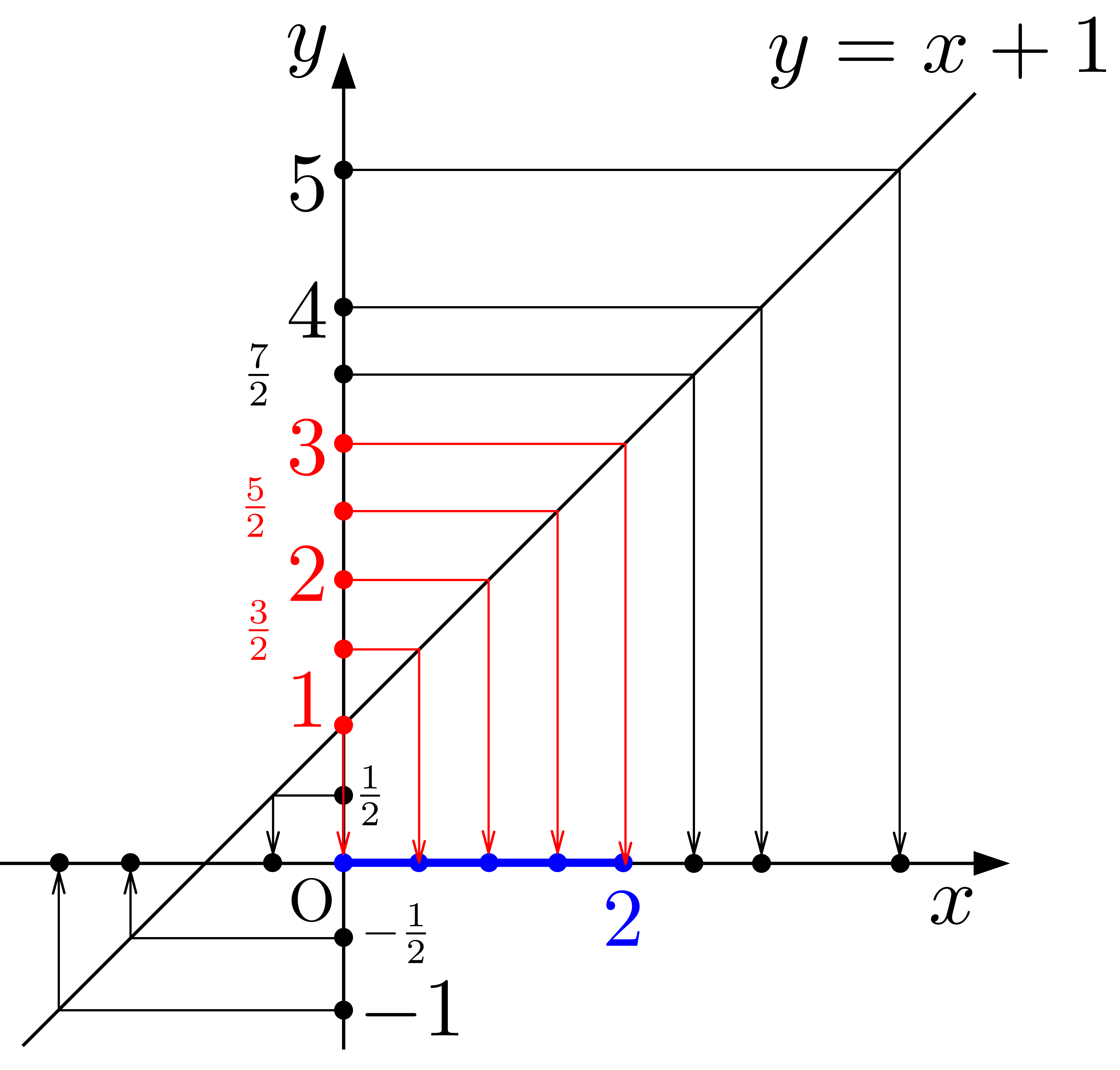しかし，「数を頭に思い浮かべて～」とは言うものの思い浮かべ得る点は当然ながら無限です．その無限の数に対し上の考察を無限回行うわけにはいきません．そこでどうするか？文字を使いましょう．頭に思い浮かべ得る数の代表の文字として\(k\)を用います．そして上と同様の同値変形を行います．すなわち，
\[\text{\(k\)は求める値域（の点の１つ）である\(~\Longleftrightarrow~\)\(k\)に対応する\(x\)が定義域内に存在する}\]
さらに同値変形を続けて，
\[
\begin{align*}
&\text{\(k\)は求める値域（の点の１つ）である}\\
\Longleftrightarrow~&\text{\(k\)に対応する\(x\)が定義域に存在する}\\
\Longleftrightarrow~&\text{\(k=x+1\)をみたす\(x\)が定義域に存在する}\\
\Longleftrightarrow~&\text{\(x=k-1\)をみたす\(x\)が定義域に存在する}\\
\Longleftrightarrow~&\text{\(x=k-1,~0 \leq x \leq 1\)をみたす\(x\)が存在する}\\
\Longleftrightarrow~&0 \leq k-1 \leq 1\\
\Longleftrightarrow~&1 \leq k \leq 2
\end{align*}
\]
よって求める値域が\(1 \leq k \leq 2\)と求まります．
今回は簡単な値域の問題でしたので，「こんな面倒なことするくらいなら（解法１）のほうがいいだろ」と思うかもしれません．が，この考え方は値域の問題ばかりではなく，軌跡や領域の問題において根幹となる重要な考え方になります．
以上の解法（考え方）「存在条件に同値変形して処理」するこの手法を，雑誌「大学への数学」では「逆手流」と名付けています．記事のタイトルはこの名称を使わせて頂きました．
また，上の論理式において「\(k\)は求める値域（の点の１つ）である」を「\(k\in \text{値域}\)」と表し，さらに全称記号と存在記号を用いて記述すると以下のようになります．
\[
\begin{align*}
&k \in \text{値域}\\
\Longleftrightarrow~&\exists x \big[\text{\(k\)に対応する\(x\)が定義域上}\big]\\
\Longleftrightarrow~&\exists x \big[\text{\(k=x+1\)をみたす\(x\)が定義域上}\big]\\
\Longleftrightarrow~&\exists x \big[\text{\(x=k-1\)をみたす\(x\)が定義域上}\big]\\
\Longleftrightarrow~&\exists x \big[\text{\(x=k-1 \land ~0 \leq x \leq 1\)}\big]\\
\Longleftrightarrow~&0 \leq k-1 \leq 1\\
\Longleftrightarrow~&1 \leq k \leq 2
\end{align*}
\]