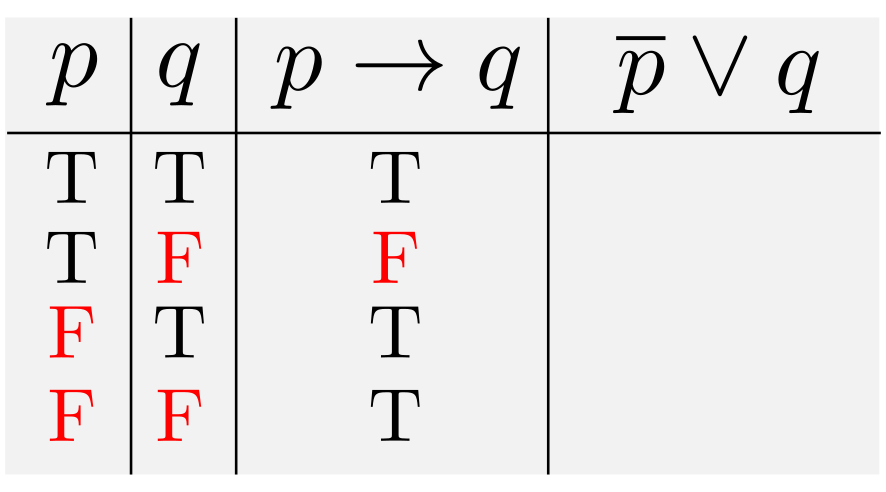
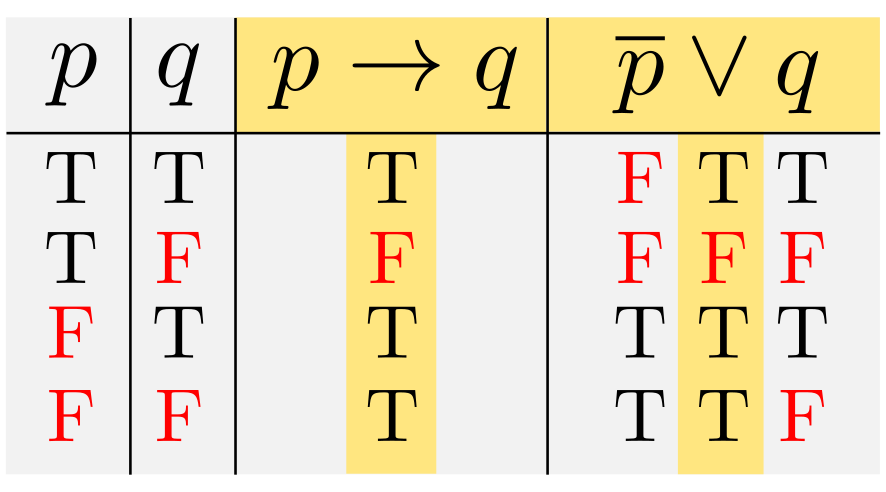
原点\(O\)からの距離と点\(A(3,0)\)からの距離の比が\(2:1\)である点\(P\)の軌跡を求めよ.
教科書では「点\(P\)の軌跡を求める手順」を次のように言っています
-
- 条件を満たす点\(P\)の座標を\((x,~y)\)として,点\(P\)に関する条件を\(x,~y\)の式で表し,この方程式が表す図形が何かを調べる.
- 逆に,で求めた図形上のすべての点\(P\)が,与えられた条件を満たすことを確かめる.
引用元:『高等学校 数学Ⅱ』数研出版
で,その解法に従った解答が,
点\(P\)に関する条件は\[OP:AP=2:1\]
これより\[2AP=OP\]
すなわち\[4AP^2=OP^2\]
\(AP^2=(x-3)^2+y^2,~OP^2=x^2+y^2\)を代入すると\(4\left\{(x-3)^2+y^2\right\}=x^2+y^2\)
整理すると\(x^2-8x+y^2+12=0\)すなわち\((x-4)^2+y^2=2^2\).
よって点\(P\)は円\((x-4)^2+y^2=2^2\)上にある.
逆に,この円上のすべての点\(P(x,~y)\)は,条件を満たす.
したがって,求める軌跡は,点\((4,~0)\)を中心とする半径\(2\)の円である.
引用元:『高等学校 数学Ⅱ』数研出版
とあります.ここで疑問.
「逆に,この円上のすべての点\(P(x,~y)\)は,条件を満たす」これは何?っていうか,なぜこんなことが言えるの?実際にその「すべての点」について「距離の比が\(2:1\)である」と調べたってこと?でも「すべての点」って,得られた図形は円だから円上の点,すなわち「無限個の点」ということでしょ?無限回計算して調べるわけ…??
…と思った人も少なくないはず.これ,疑問を持つほうが自然で,その人の理解力が無いんじゃなく,はっきり言って教科書のほうが悪い.まさに教科書特有のダメダメ記述の代表格.にもかかわらず何のフォローもないという.結果どうするか?「良く分からないから覚えよう」になる.だからあまり深く考えない人ほどテキトーにスルーして得点できる.こんな勉強を強いられる(真面目な)高校生が本当かわいそう.
別解を示します.
解答
\[
\begin{align}
&OP:AP=2:1\\
\Longleftrightarrow &~2AP=OP\\
\Longleftrightarrow &~4AP^2=OP^2\\
\Longleftrightarrow &~4\left\{(x-3)^2+y^2\right\}=x^2+y^2\\
\Longleftrightarrow &~x^2-8x+y^2+12=0\\
\Longleftrightarrow &~(x-4)^2+y^2=2^2\\
\end{align}
\]
したがって,求める軌跡は,点\((4,~0)\)を中心とする半径\(2\)の円.
このようにかけば逆の考察など必要ありません.その理由は,上のように一連の式の間の論理関係を見てらえればわかりますが,どれも同値変形だからです.このような同値記号を用いた記述であれば,このこと,すなわち「各式は明らかに同値だから,逆の考察はしないよ」という意思表示になっています.だから逆の考察は必要ない,というわけです.
対して,教科書の解答はどういう意図のもとに「逆に~」を書いているのでしょうか.解答では「これより」「すなわち」「整理すると」「よって」…という(数学的定義のない)日本語を多用しているところを見るに,各段階において十分性を意識せずに変形している,と考えられます(「最初に十分性を追わずに必要性だけ追っていき,あとで別枠で十分性を調べる」という論法自体は数学ではよく見られる方法で,それ自体は問題はありません).論理式で書けば
\[
\begin{align}
&OP:AP=2:1\\
\Longrightarrow &~2AP=OP\\
\Longrightarrow &~4AP^2=OP^2\\
\Longrightarrow &~4\left\{(x-3)^2+y^2\right\}=x^2+y^2\\
\Longrightarrow &~x^2-8x+y^2+12=0\\
\Longrightarrow &~(x-4)^2+y^2=2^2\\
\end{align}
\]
という構造になっているので,最後に元の条件と同値であるかどうか確認が求められる,だから上の論理式において「\(\Leftarrow\)も言えるよ」という意味で「逆に,この円上のすべての点\(P(x,~y)\)は,条件を満たす.」と書いたのでしょう.しかしこれもかなり譲歩して読み取ればの話で,解答の書き方では冒頭に記したように「\((x-4)^2+y^2=2^2\)をみたすすべての点,つまり無限個の点について距離の比が\(2:1\)であると無限回調べた」としか読み取れないと思うんですがね.
もちろん教科書特有の色々な制約の下でのやむを得ない記述なんでしょうけど,正直者が馬鹿を見る(真面目な;思慮深い生徒が躓く)的な記述はいかがなものか,と思う.せめて解答欄外でフォローしようよ,と思いますね.これだから教科書至上主義は危険です.
「いやそんなややこしいこと考えずともに最後に『逆に~』の一言を書いときゃそれでOKでしょ点数は貰えるし」と思う人.それは教科書レベルでの話.少し発展的な問題になると痛い目にあいますよ.