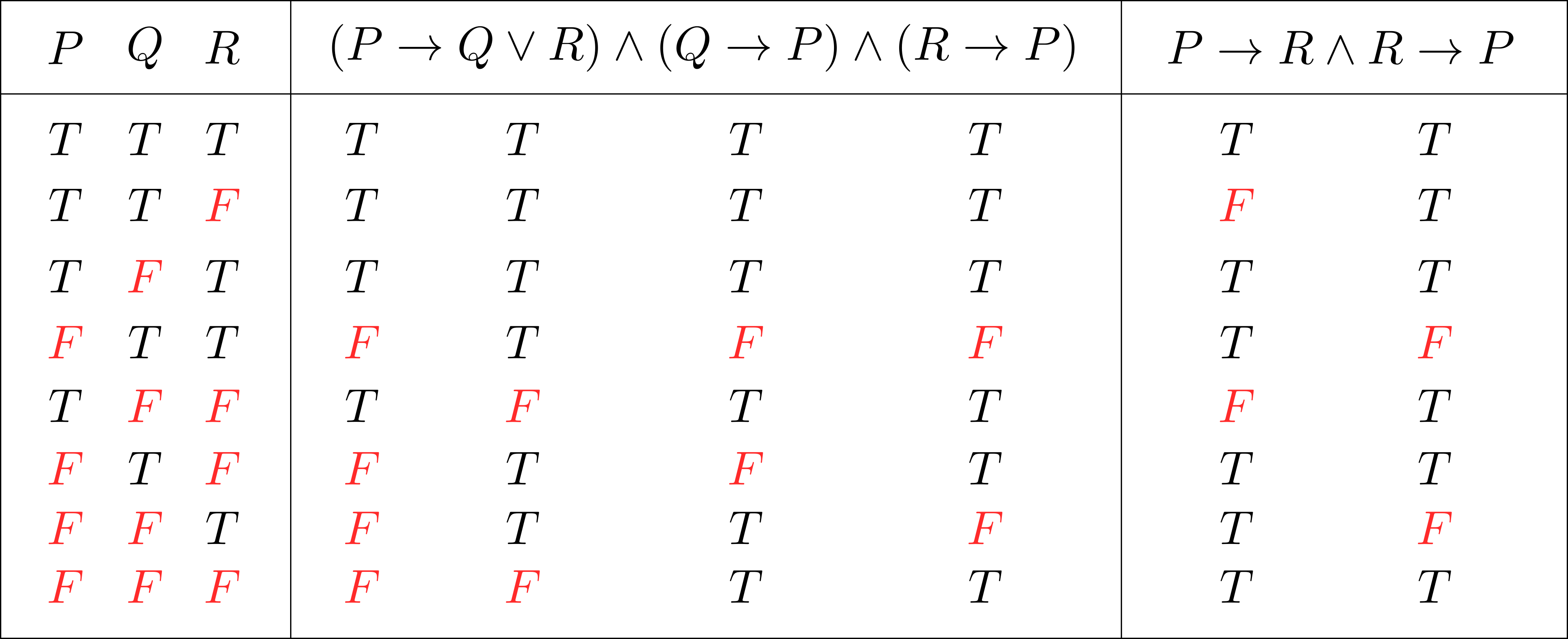
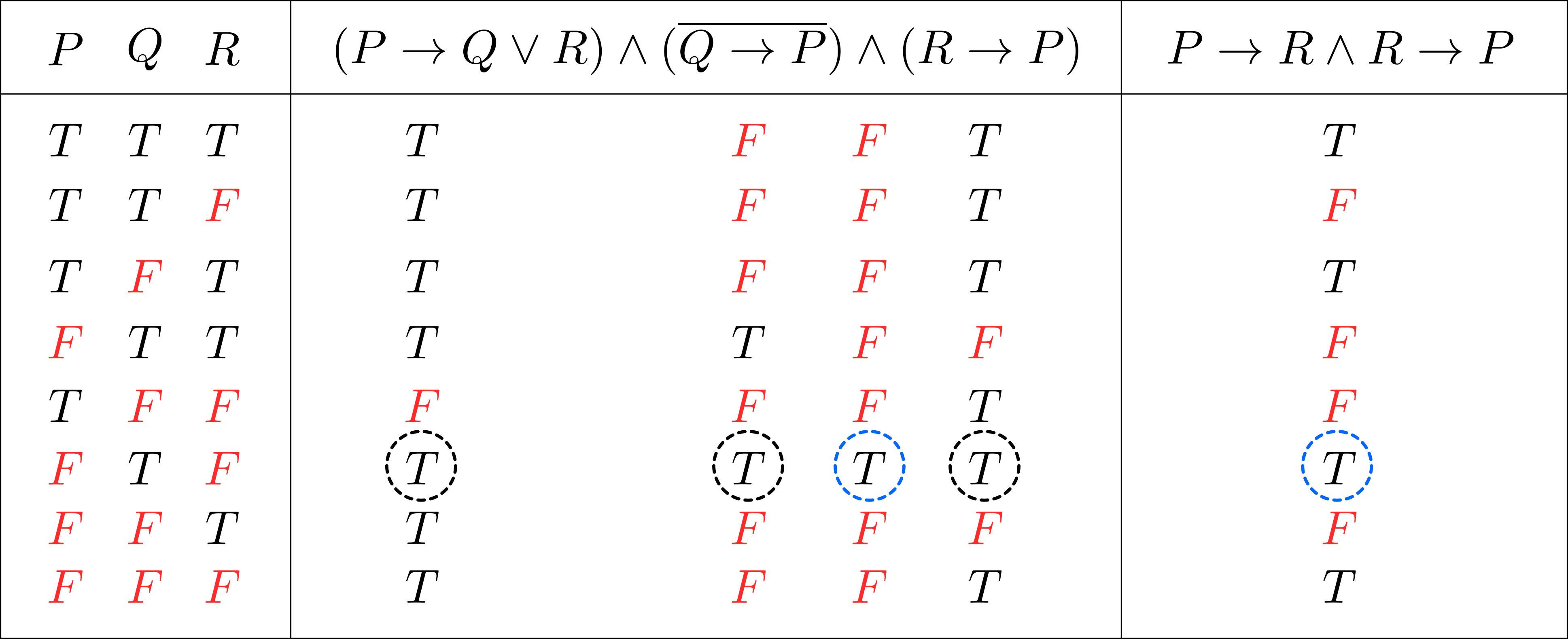
解答
\begin{align*}
&a(|x|-a)+x+1<0 \land a>-1\\
\Longleftrightarrow~&a(|x|-a)+x+1<0 \land a>-1 \land (x \geq 0 \lor x <0)\\
\Longleftrightarrow~&(a(x-a)+x+1<0 \land a>-1 \land x \geq 0)\\
&\lor (a(-x-a)+x+1 < 0 \land a>-1 \land x < 0)\\
\Longleftrightarrow~&((a+1)x < a^2-1 \land a+1>0 \land x \geq 0)\\
&\lor ((1-a)x < a^2-1 \land a > -1 \land x < 0)\\
\Longleftrightarrow~&(x < a-1 \land a+1>0 \land x \geq 0) \\
&\lor ((1-a)x < a^2-1 \land a > -1 \land x < 0)\\
\Longleftrightarrow~&((x < a-1 \land a+1>0 \land x \geq 0)\land(a-1\leq 0 \lor a-1 >0)) \\
&\lor (((1-a)x < a^2-1 \land a > -1 \land x < 0)\land (1-a>0\lor 1-a=0 \lor 1-a <0))\\
\Longleftrightarrow~&(x < a-1 \land a+1>0 \land x \geq 0 \land a-1\leq 0) \\
&\lor(x < a-1 \land a+1>0 \land x \geq 0 \land a-1 >0) \\
&\lor ((1-a)x < a^2-1 \land a > -1 \land x < 0 \land 1-a>0)\\
&\lor ((1-a)x < a^2-1 \land a > -1 \land x < 0 \land 1-a=0)\\
&\lor ((1-a)x < a^2-1 \land a > -1 \land x < 0 \land 1-a <0)\\
\Longleftrightarrow~&(x < a-1 \land x \geq 0 \land -1 < a \leq 1) \\
&\lor(x < a-1 \land a > -1 \land x \geq 0 \land a >1) \\
&\lor (x < -a-1 \land x < 0 \land -1 < a < 1)\\
&\lor (0x < 0 \land a > -1 \land x < 0 \land a=1)\\
&\lor (x > -a-1 \land a > -1 \land x < 0 \land 1 < a)\\
\Longleftrightarrow~&\bot\\
&\lor(x < a-1 \land x \geq 0 \land a >1) \\
&\lor (x < -a-1 \land x < 0 \land -1 < a < 1)\\
&\lor \bot\\
&\lor (x > -a-1 \land x < 0 \land 1 < a)\\
\Longleftrightarrow~&(x < a-1 \land x \geq 0 \land a >1) \\
&\lor (x < -a-1 \land x < 0 \land -1 < a < 1)\\
&\lor (x > -a-1 \land x < 0 \land 1 < a)\\
\Longleftrightarrow~& (x < -a-1 \land -1 < a < 1)\\
&\lor(x < a-1 \land x \geq 0 \land a >1) \\
&\lor (x > -a-1 \land x < 0 \land 1 < a)\\
\Longleftrightarrow~& (x < -a-1 \land -1 < a < 1)\\
&\lor (((x < a-1 \land x \geq 0) \lor (x > -a-1 \land x < 0 )) \land 1 < a)\\
\Longleftrightarrow~& (x < -a-1 \land -1 < a < 1)\\
&\lor ((0 \leq x < a-1 \lor -a-1< x < 0 ) \land 1 < a)\\
\Longleftrightarrow~& (x < -a-1 \land -1 < a < 1)\lor (-a-1< x < a-1 \land 1 < a )
\end{align*}
解答終