\begin{align*}
f^{\prime}(x)=&1\cdot (\log x)^2+x\cdot 2(\log x)\frac{1}{x}-2\left(\log x+x\cdot \frac{1}{x}\right)+\frac{3}{2}\\
=&(\log x)^2+2\log x-2\log x-2+\frac{3}{2}\\
=&(\log x)^2-\frac{1}{2}
\end{align*}
\(f^\prime(x)=0\)を解くと,\begin{align*}
&(\log x)^2-\frac{1}{2}=0\\
\Longleftrightarrow &~\left(\log x -\frac{1}{\sqrt{2}}\right)\left(\log x +\frac{1}{\sqrt{2}}\right)=0\\
\Longleftrightarrow &~\log x = \frac{1}{\sqrt{2}}\\
\Longleftrightarrow &~x=e^{\frac{1}{\sqrt{2}}}
\end{align*}
さて,増減表ですが,例の「\(f(x)=0\)を満たす\(x\)を挟む\(x\)を代入して調べる」方法をとるとすれば,\(1\leq x \leq e^\frac{1}{\sqrt{e}}\)そして\(e^\frac{1}{\sqrt{e}} \leq x \leq e\)を満たす\(x\)を見つけ,それを\(f^{\prime}(x)=(\log x)^2-\frac{1}{2}\)に代入するわけですが…そんなことはとてもじゃないがやってられない。
そこで,以下のように考えます:
\begin{align*}
f^{\prime}(x)=&(\log x)^2-\frac{1}{2}=\left(\log x -\frac{1}{\sqrt{2}}\right)\left(\log x +\frac{1}{\sqrt{2}}\right)
\end{align*}ここで,\(f^{\prime}(x)\)の正負に関わるのは\(\left(\log x -\frac{1}{\sqrt{2}}\right)\)の部分だけですから,この部分だけに着目することにします。ここで前回の「増減表のかきかた」で紹介したように「絵をかく」ことを考えますが,ここでさらに一工夫。着目している\(\log x -\frac{1}{\sqrt{2}}\)を,\(y=\log x\)と\(y=\frac{1}{\sqrt{2}}\)との差,という「2つの関数の差」と見なすことで以下のように視覚化できます。
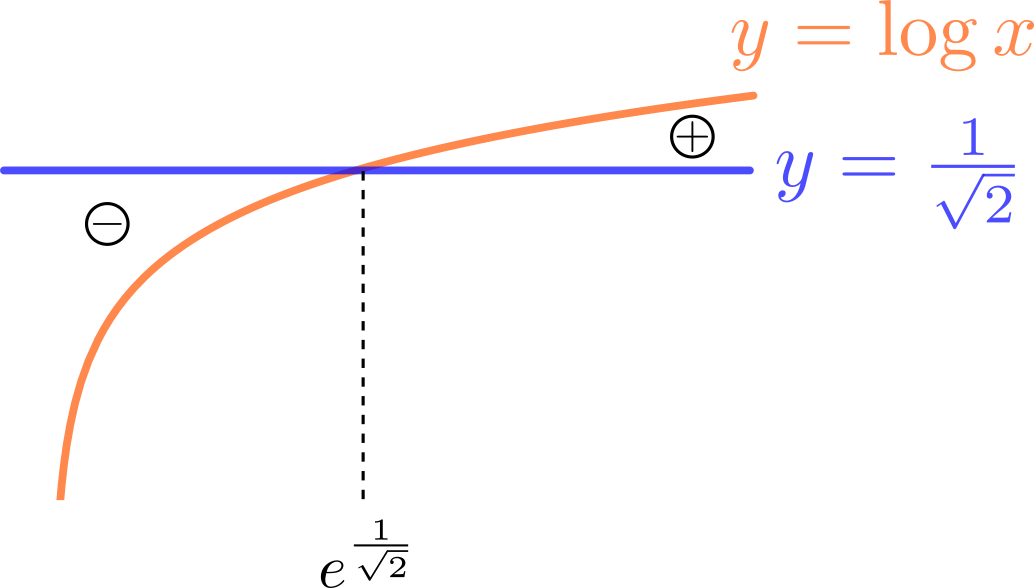
\(y=\log x\)が‘上’なら正,\(y=\frac{1}{\sqrt{2}}\)が‘上’なら負ですから,結局\(f^{\prime}(x)\)の符号は\(e^{\frac{1}{\sqrt{2}}}\)を境に\(-\rightarrow+\)と変化することが直ちに分かります。
他にも例えば,
であれば,\(f^{\prime}(x)=e^x(\sin x+\cos x)\)となりますが,これなら\(\sin x-(-\cos x)\)という「関数の差」と見なすことで,以下のように増減の様子が即断できます(しかも\(f^{\prime}(x)=0\)をみたす\(x\)が\(\frac{3}{4}\pi\)であることも分かるというオマケつき)。これを「具体的な\(x\)を代入して調べる」なんていう〇〇なことはやるべきじゃない。
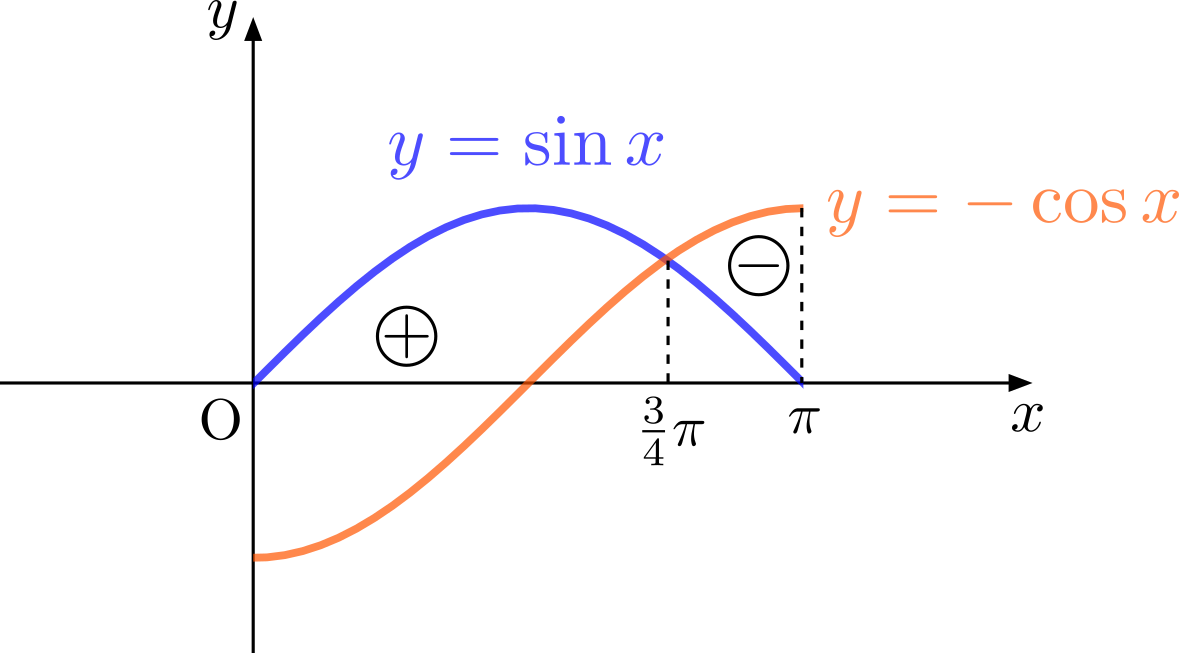
増減表のかきかた(\(f^{\prime}(x)\)の行の埋め方)をまとめると,
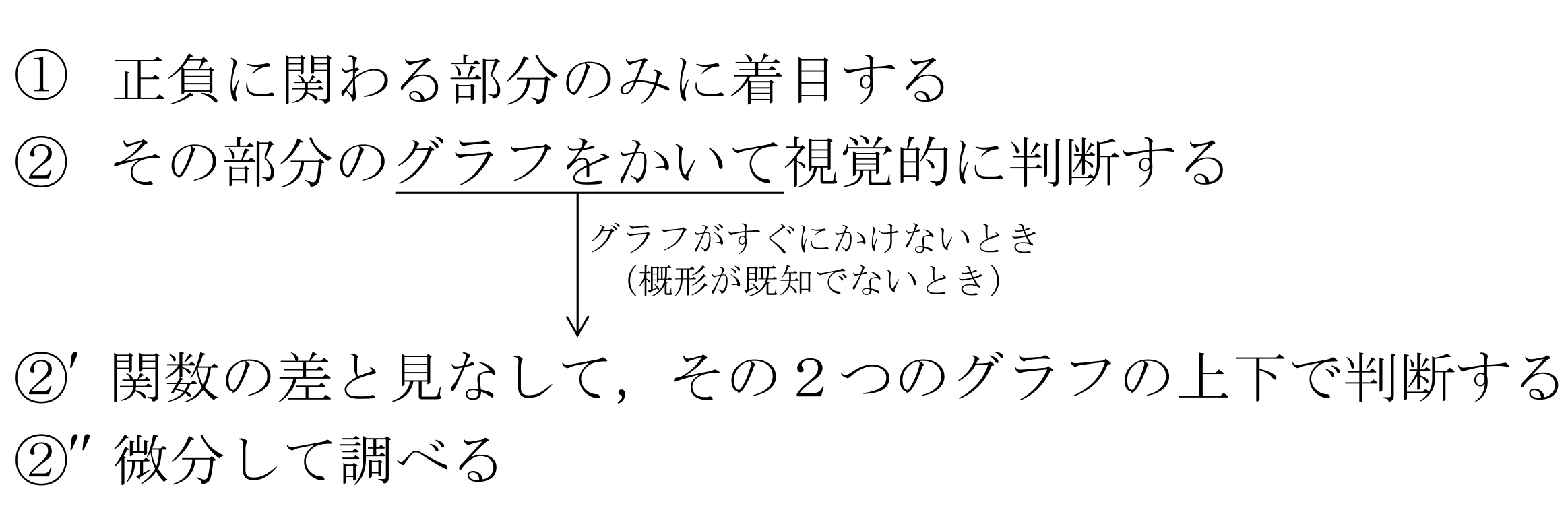
となります。数学Ⅱにおいては,すべて②のみで片付きます。数Ⅲにおいてもほとんどが②’までで片付きます。
上の例から見て分かる通り,「具体的な\(x\)を代入して調べる」という手法が通用するのはせいぜい教科書の例題までで,やっていることは間違いではないものの,入試問題では応用が効かないのです。だからダメダメなんです。にもかかわらず,こんな手法をドヤ顔で教えるのはいかがなものでしょうかね。皆がそうしてるから,教科書にそう書いてあるから,は理由にならんでしょ…と個人的に思います。


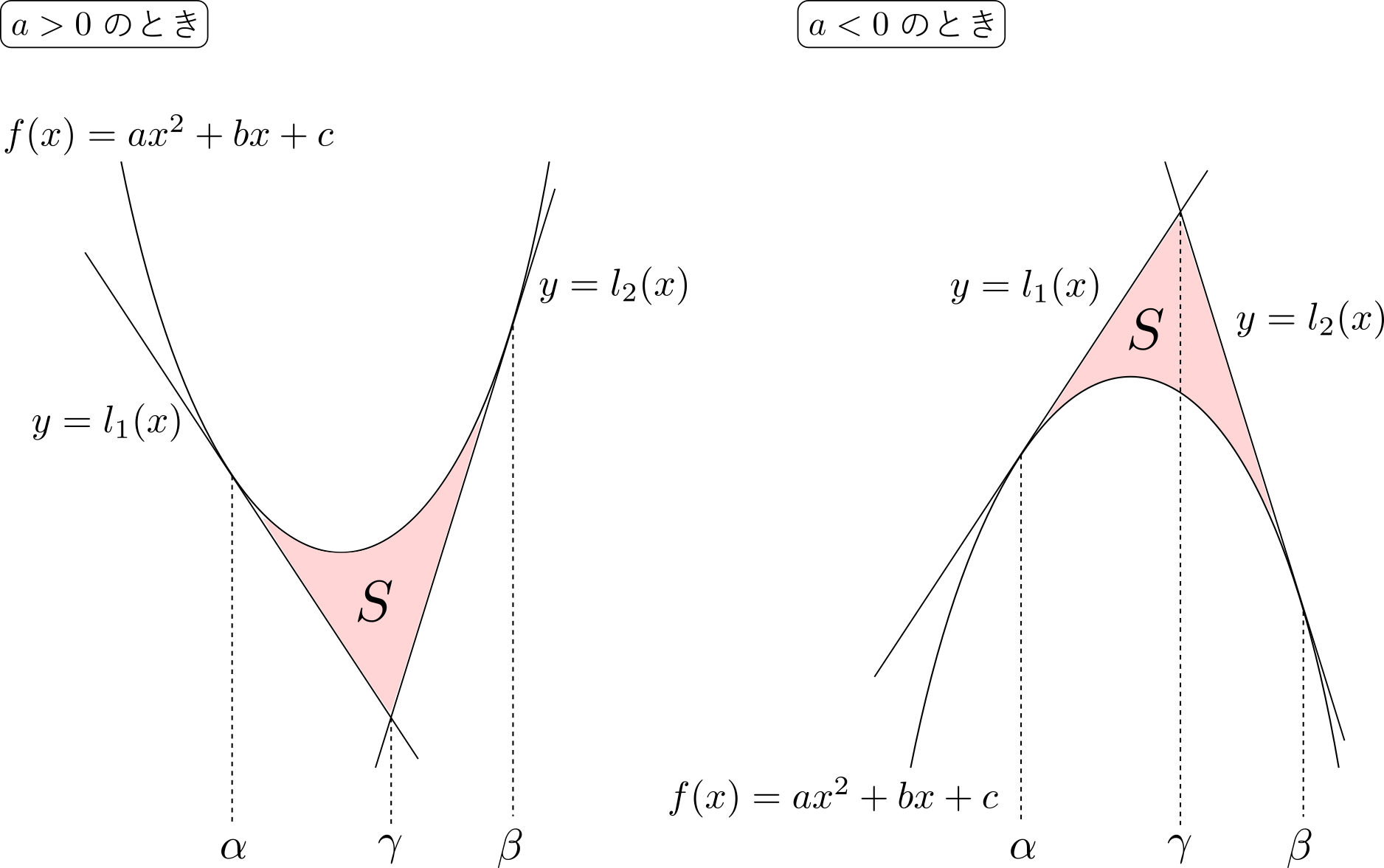
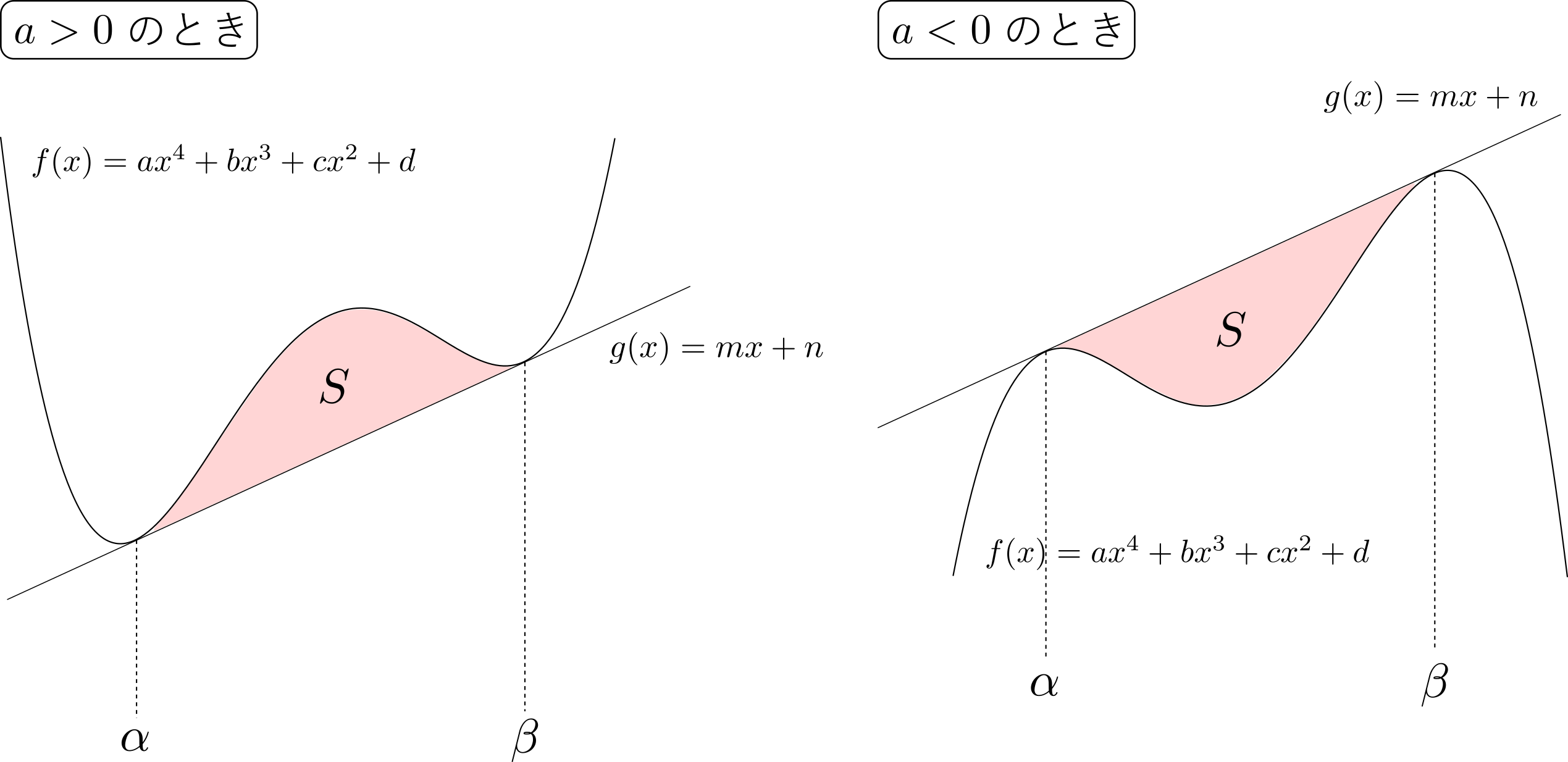
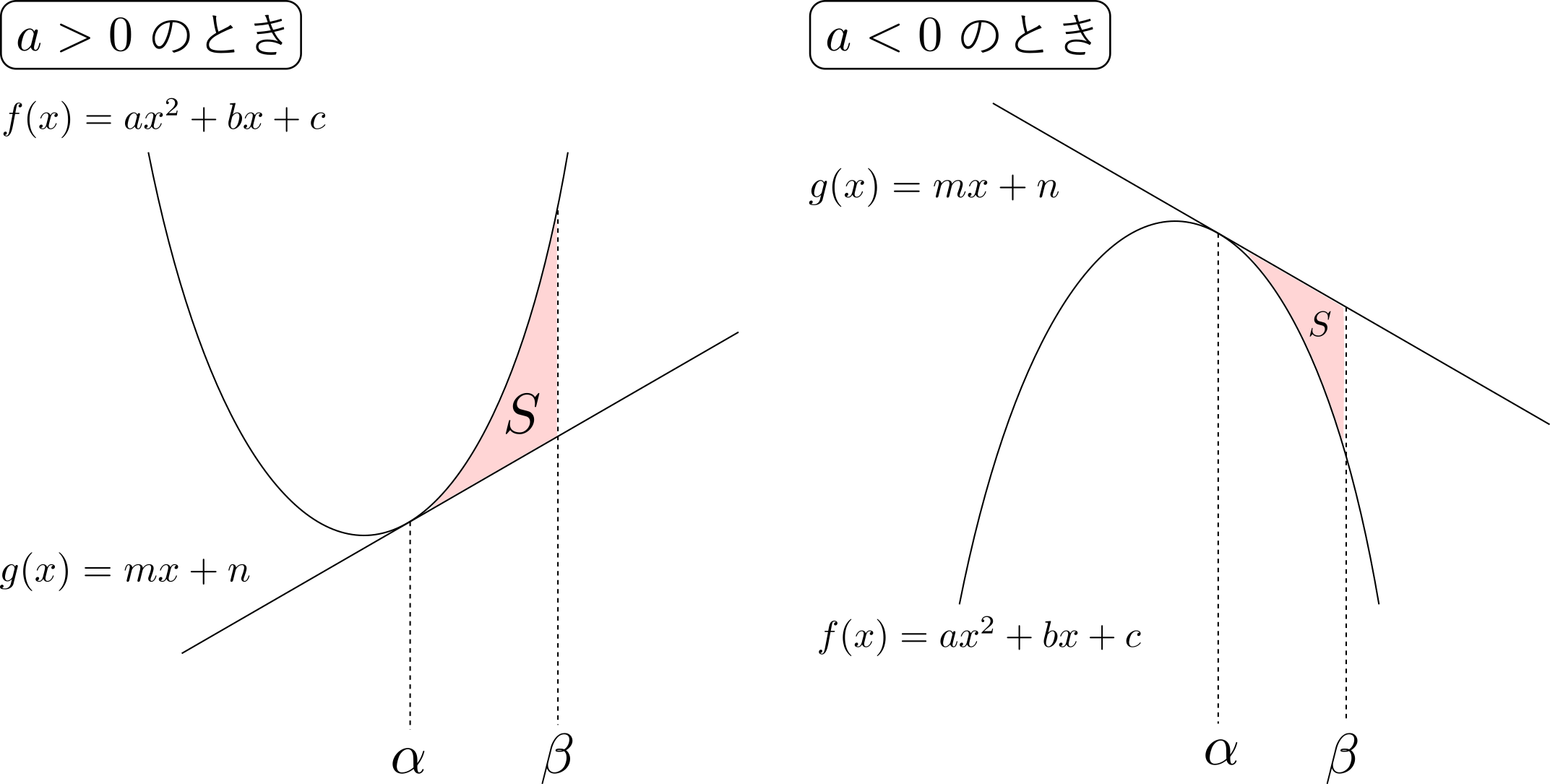
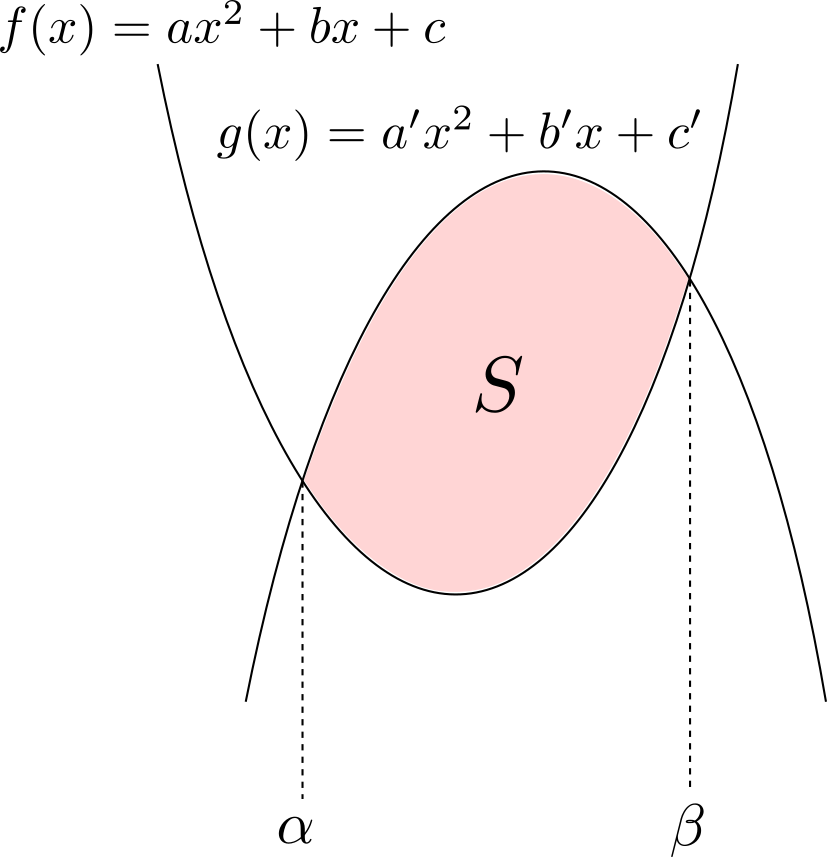
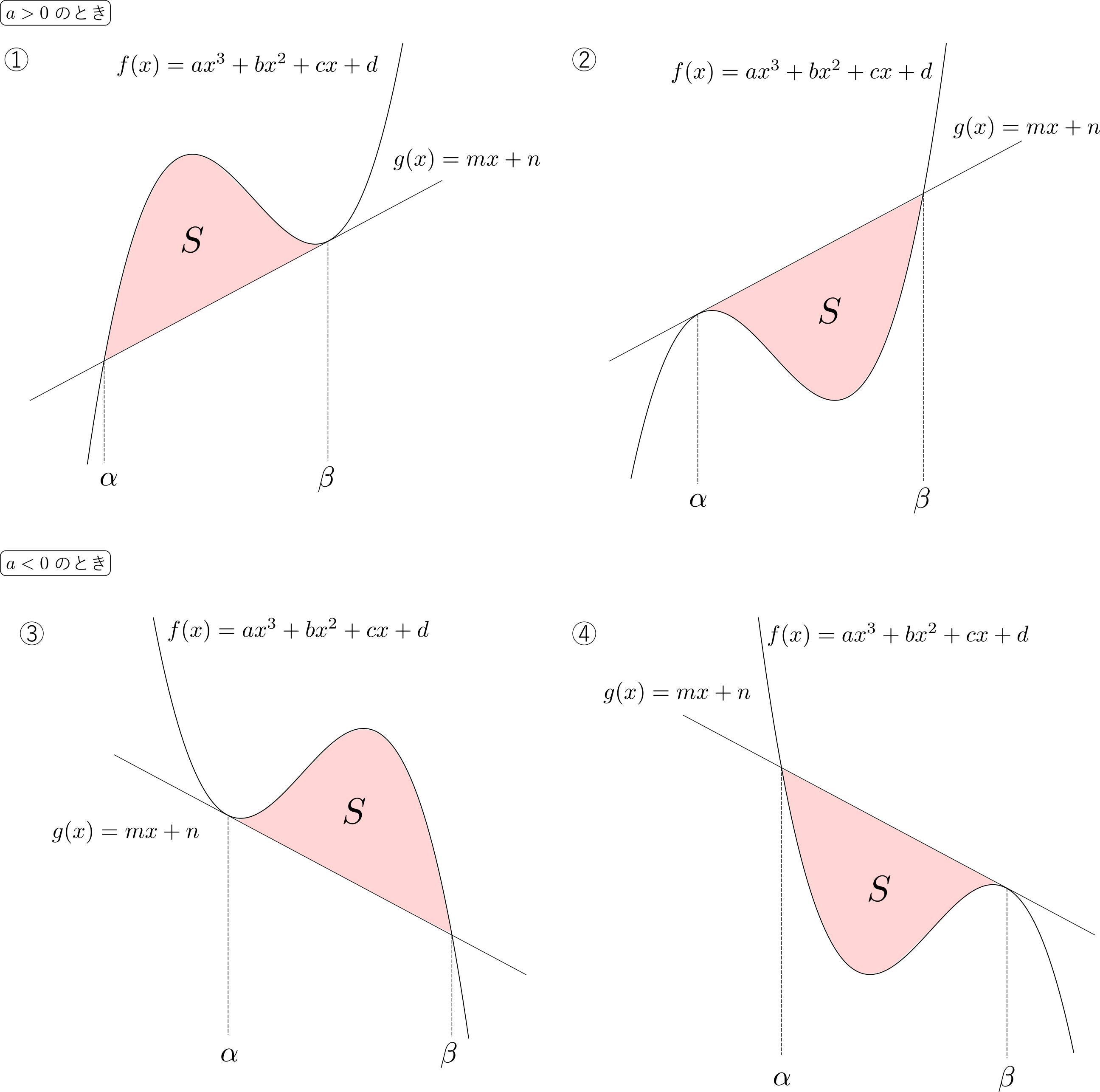 上の曲線と直線で囲まれる部分の面積\(S\)は,いずれの場合も\[S = \frac{|a|(\beta-\alpha)^4}{12}\]で表される.
上の曲線と直線で囲まれる部分の面積\(S\)は,いずれの場合も\[S = \frac{|a|(\beta-\alpha)^4}{12}\]で表される.