(数学Ⅲ)
不等式の証明のアプローチのひとつとして微分法の利用があります。
証明
まず\(b\geq 0\)を固定して,\[ab \leq \frac{a^p}{p}+\frac{b^q}{q} \Longleftrightarrow~ \frac{1}{p}a^p-ba+\frac{b^q}{q}\geq 0\]と変形し,左辺を\(a\)の関数と見なす.この関数を\(f(a)\)とおく:\[f(a)=\frac{1}{p}a^p-ba+\frac{b^q}{q} \quad (a\geq 0)\]\(f^{\prime}(a)\)を調べると,\[f^{\prime}(a)=a^{p-1}-b\]\(a^{p-1}\)の概形が分からないので,もう一度微分することで\(f^{\prime}(a)\)がどんな概形かを調べる(※).すると\[f^{\prime\prime}(a)=(p-1)a^{p-2}\geq 0\]したがって\(f^{\prime}(a)\)は増加関数であることが分かる.\(a\geq 0\)であったことに注意して\(a=0\)のときの\(f^{\prime}(a)\)の値を調べると\[f^{\prime}(0)=-b\]
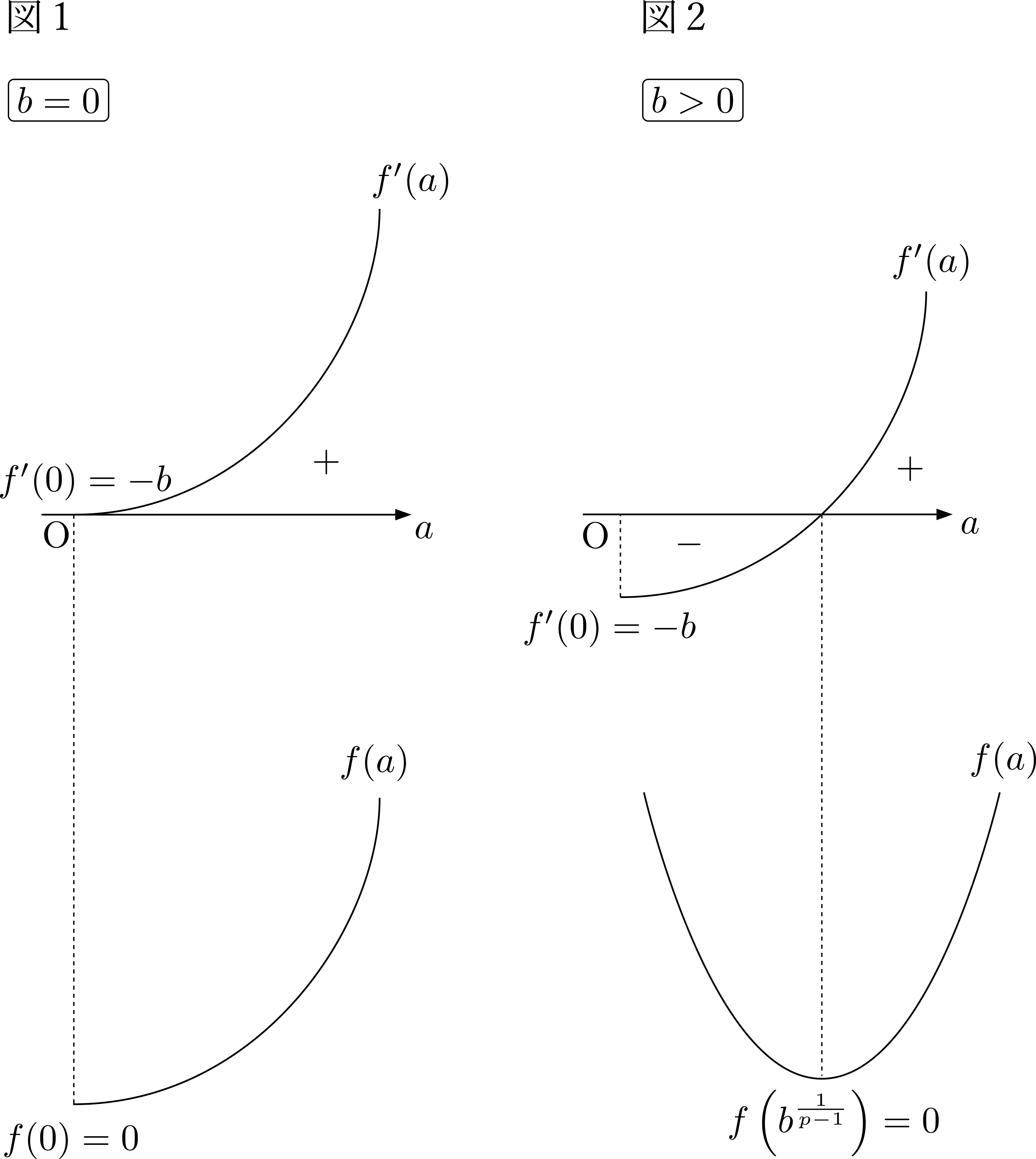
\(b=0\)のときは,\(f^{\prime}(0)=0\)であるから\(f^{\prime}(a)\geq 0\)となる.\(f(0)\)を調べると\(f(0)=\frac{b^q}{q}= 0\)であるから\(f(a)\geq 0\).(図1)
\(b>0\)のときすなわち\(-b<0\)のときは,\(f^{\prime}(a)=a^{p-1}-b=0 \Longleftrightarrow a=b^{\frac{1}{p-1}}\)で最小値をとる.
そこで\(f\left(b^{\frac{1}{p-1}}\right)\)を調べると
\begin{align*}
f\left(b^{\frac{1}{p-1}}\right)=&\frac{1}{p}\left(b^{\frac{1}{p-1}}\right)^p-b\cdot b^{\frac{1}{p-1}}+\frac{b^q}{q}\\
=&\frac{1}{p}b^{\frac{p}{p-1}}-b^{\frac{p}{p-1}}+\frac{b^q}{q}
\end{align*}
ここで,\(\frac{1}{p}+\frac{1}{q}=1\Leftrightarrow q=\frac{p}{p-1}\)であるから,\[f\left(b^{\frac{1}{p-1}}\right)=\frac{1}{p}b^q-b^q+\frac{1}{q}b^q=\left(\frac{1}{p}+\frac{1}{q}-1\right)b^q=0\]したがって\(f(a)\geq 0\).(図2)
以上により\[ab \leq \frac{a^p}{p}+\frac{b^q}{q}\]が示された.
証明終
※は概形が図示できず,かつ「差」とみても把握できないタイプなのでもう一回微分して\(f^{\prime\prime}(a)\)を調べました。この記事の「増減表のかきかた」の②”にあたる状況です。







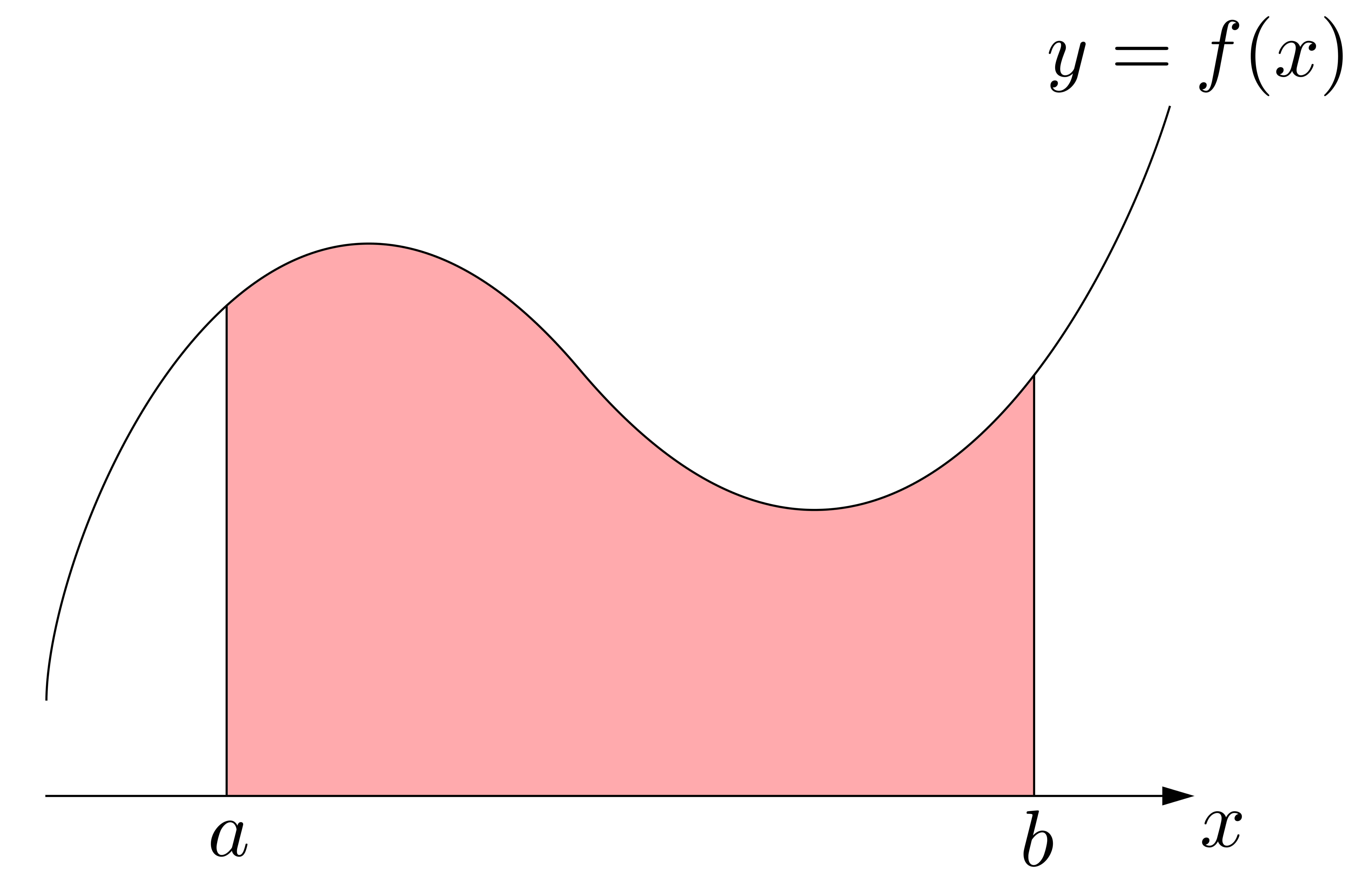
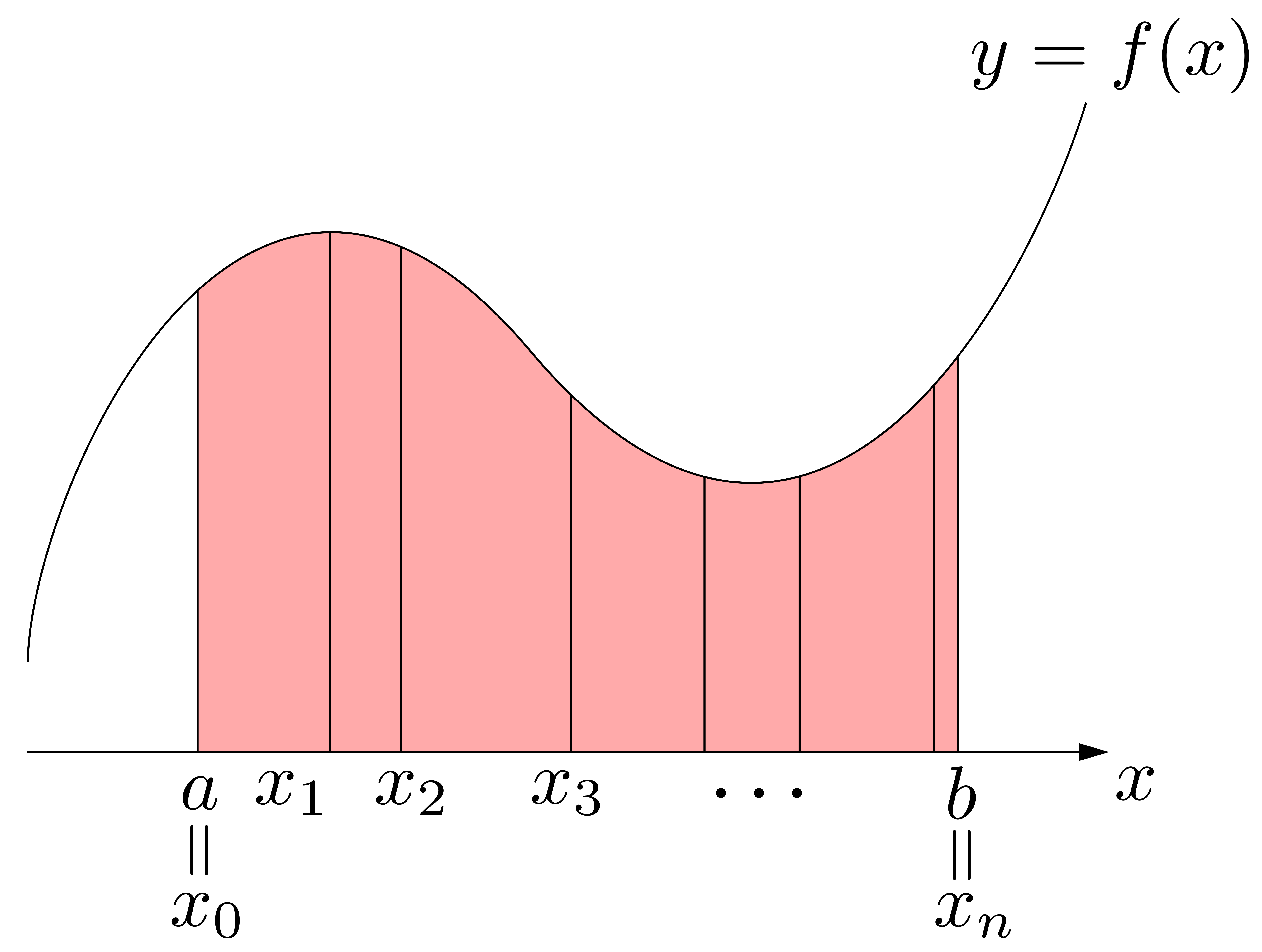
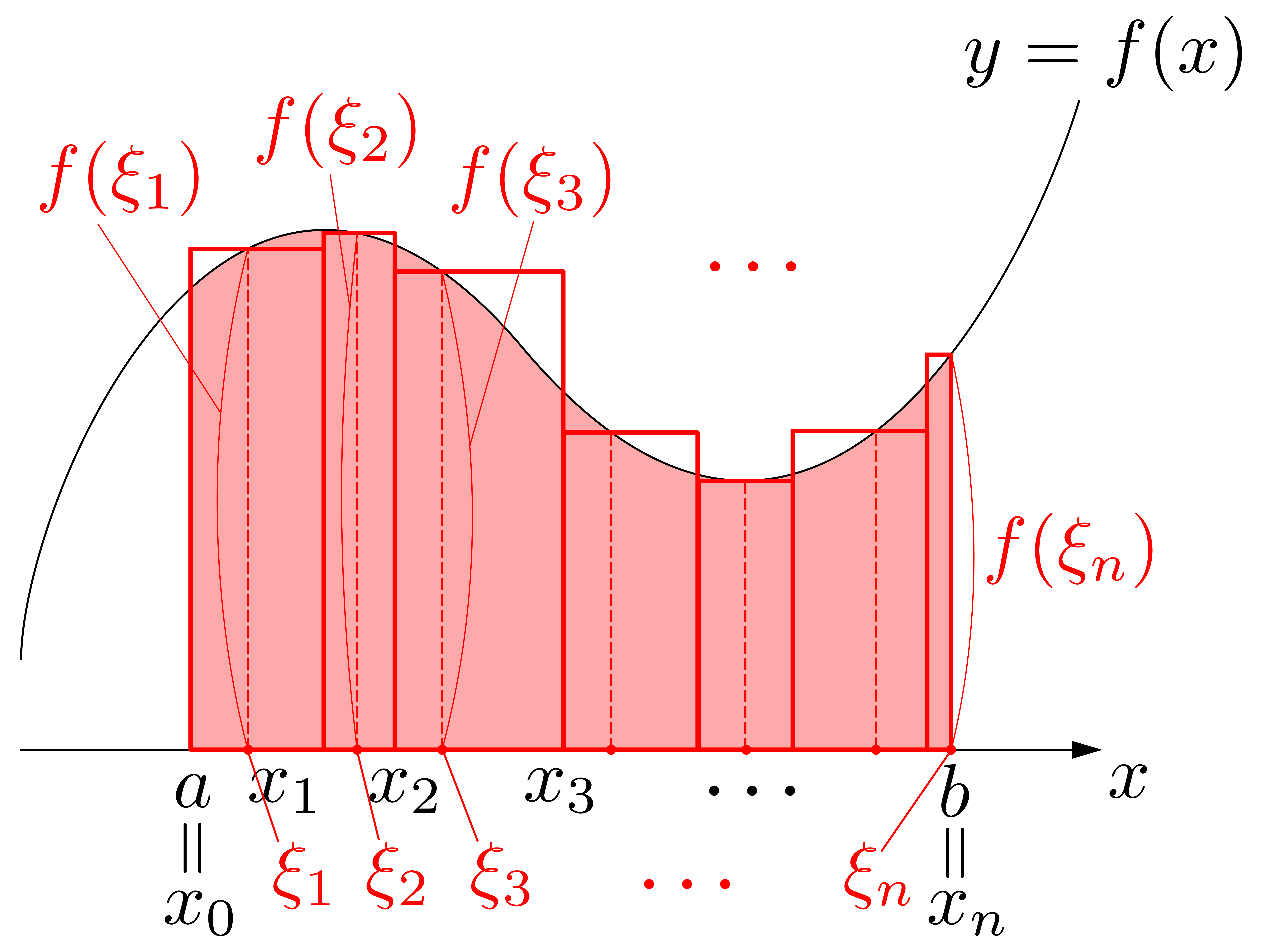

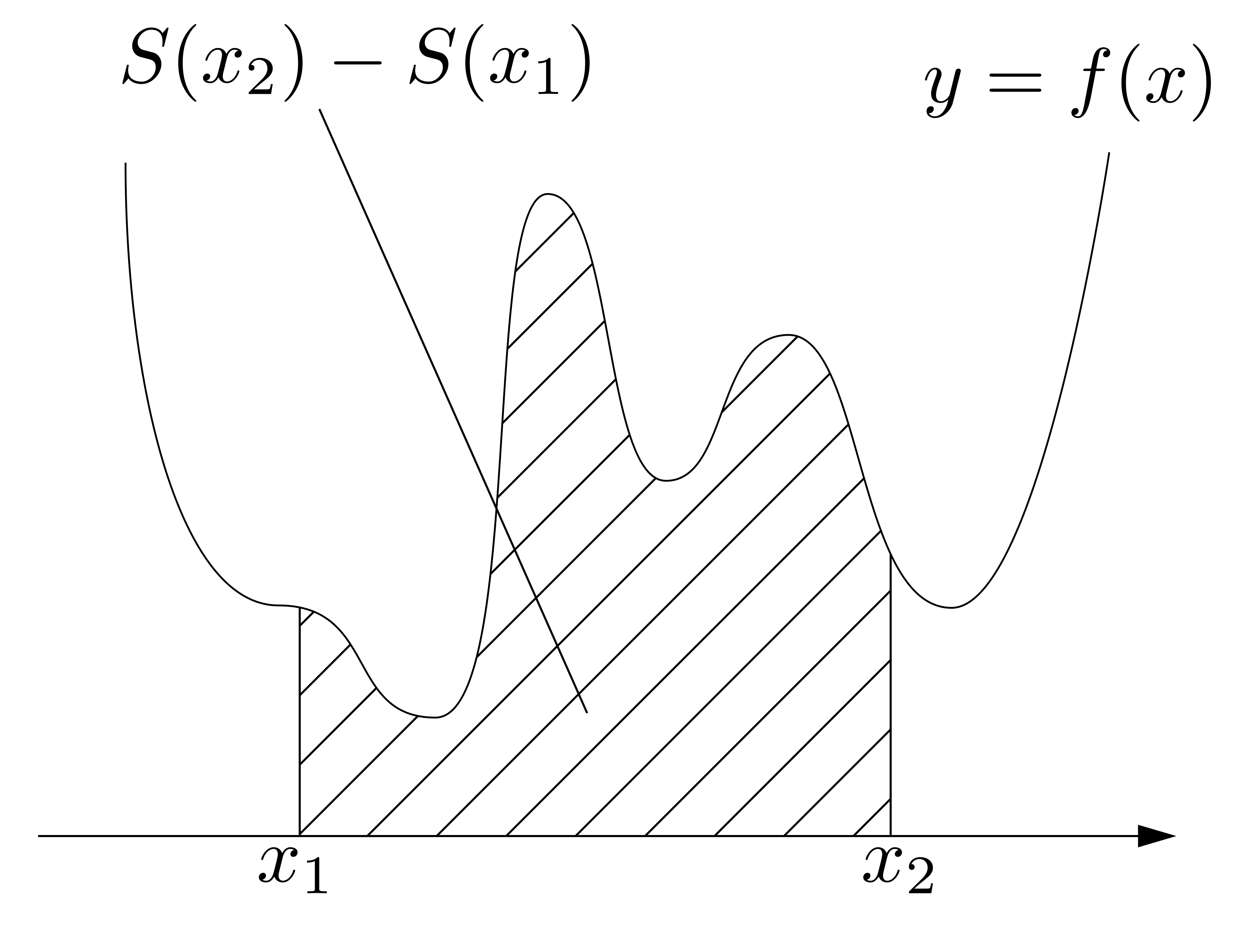
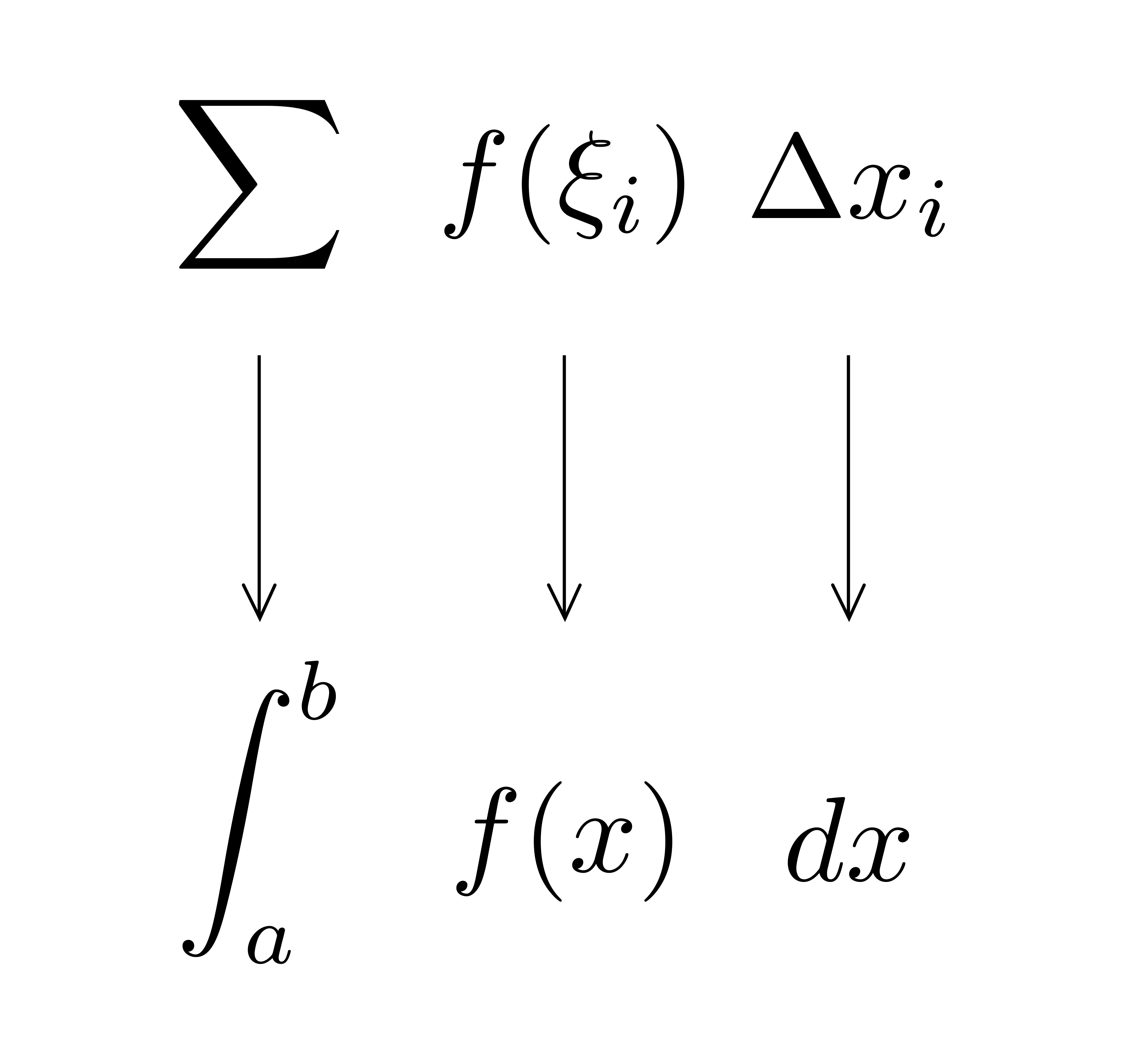 以上を見ると,\(\displaystyle \int^b_a f(x)dx\)の\(\displaystyle \int\)や\(dx\)の「イメージ」が見えてきます.右図に示すように,\(\displaystyle \sum\)が\(\displaystyle \int\)に,\(\Delta x_i\)が\(dx\)と対応しているわけです.
以上を見ると,\(\displaystyle \int^b_a f(x)dx\)の\(\displaystyle \int\)や\(dx\)の「イメージ」が見えてきます.右図に示すように,\(\displaystyle \sum\)が\(\displaystyle \int\)に,\(\Delta x_i\)が\(dx\)と対応しているわけです.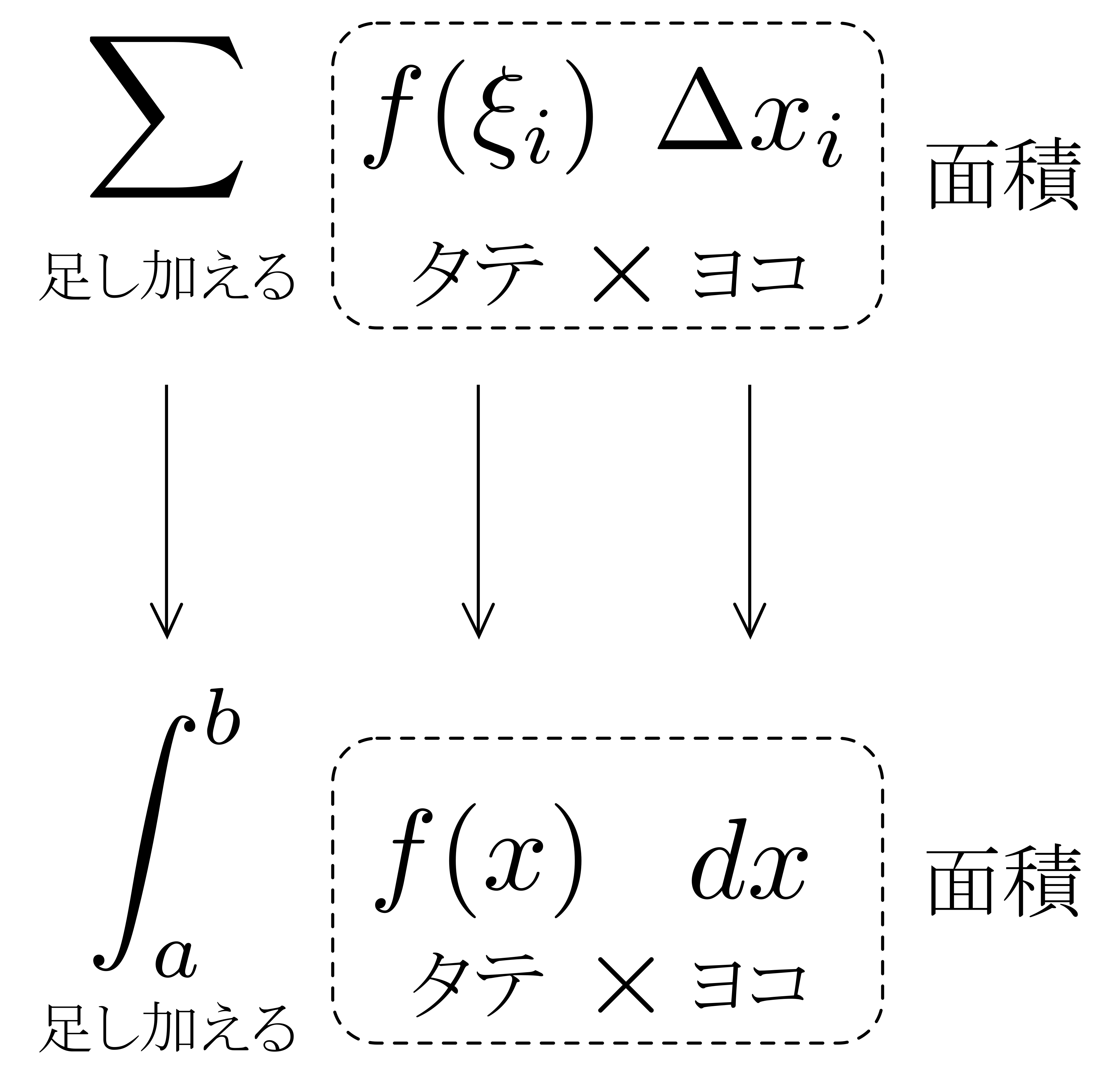 以上を踏まえて\(\displaystyle \int^b_a f(x)dx\)を眺めると,これは「微小面積\(f(x)\times dx\)を\(\displaystyle \int\)したもの(連続的に足し加えたもの)」と読み取れることが分かります!
以上を踏まえて\(\displaystyle \int^b_a f(x)dx\)を眺めると,これは「微小面積\(f(x)\times dx\)を\(\displaystyle \int\)したもの(連続的に足し加えたもの)」と読み取れることが分かります!