事象\(\mathrm{A,~B}\)が独立であるとき,\(\mathrm{A^c,~B^c}\)は独立です.また,事象\(\mathrm{A,~B,~C}\)が独立であるとき,\(\mathrm{A^c,~B^c,~C^c}\)は独立です.証明は高校数学でもお馴染みの公式をガチャガチャやれば出来ます.では,一般の場合はどうでしょうか?
\[\mathrm{A_1,~A_2,~\cdots,~A_n}~\text{が独立}~\Longrightarrow \mathrm{A_1^c,~A_2^c,~\cdots,~A_n^c}~\text{が独立}\]
証明
\[\mathrm{A_1,~A_2,~\cdots,~A_n}~\text{が独立}~\Longrightarrow \mathrm{A_1^c,~A_2,~\cdots,~A_n}~\text{が独立}\cdots{(\ast)}\]が示せればよい.実際,もしこれが言えたとすると,
\[
\begin{align*}
\mathrm{A_1,~A_2,~\cdots,~A_n}~\text{が独立}~&\Longrightarrow \mathrm{A_1^c,~A_2,~\cdots,~A_n}~\text{が独立}\\
&\Longleftrightarrow \mathrm{A_2,~A_3~\cdots,~A_n,~A_1^c}~\text{が独立}\\
&\Longrightarrow \mathrm{A_2^c,~A_3~\cdots,~A_n,~A_1^c}~\text{が独立}\\
&\Longleftrightarrow \mathrm{A_3,~A_4,~\cdots,~A_n,~A_1^c,~A_2^c}~\text{が独立}\\
&\Longrightarrow \mathrm{A_3^c,~A_4,~\cdots,~A_n,~A_1^c,~A_2^c}~\text{が独立}\\
&\Longleftrightarrow \mathrm{A_4,~A_5,~\cdots,~A_n,~A_1^c,~A_2^c,~A_3^c}~\text{が独立}\\
&\Longrightarrow ~\cdots\\
&\Longleftrightarrow \mathrm{A_1^c,~A_2^c,~A_3^c,~\cdots,~A_n^c}~\text{が独立}\\
\end{align*}
\]
とできます.\((\ast)\)を示します.
\[
\begin{align*}
P(\mathrm{A_2\cap A_3\cap \cdots \cap A_n})=&P(\mathrm{\Omega \cap A_2\cap A_3\cap \cdots \cap A_n})\\
=&P(\mathrm{(A_1\cup A_1^c) \cap A_2\cap A_3\cap \cdots \cap A_n})\\
=&P(\mathrm{(A_1 \cap A_2\cap A_3\cap \cdots \cap A_n)\cup (A_1^c \cap A_2\cap A_3\cap \cdots \cap A_n}))\\
=&P(\mathrm{A_1 \cap A_2\cap A_3\cap \cdots \cap A_n)+P(A_1^c \cap A_2\cap A_3\cap \cdots \cap A_n})\\
\end{align*}
\]
したがって,
\[P(\mathrm{A_2\cap A_3\cap \cdots \cap A_n)=P(A_1 \cap A_2\cap A_3\cap \cdots \cap A_n)+P(A_1^c \cap A_2\cap A_3\cap \cdots \cap A_n})\]を得ます.仮定より,\(\mathrm{A_1,~A_2,~\cdots~,A_n}\)の独立性から,\[\mathrm{P(A_2)P(A_3) \cdots P(A_n)=P(A_1)P(A_2)P(A_3) \cdots P(A_n)+P(A_1^c \cap A_2\cap A_3\cap \cdots \cap A_n})\]とでき,さらに変形すると\[\mathrm{P(A_1^c \cap A_2\cap A_3\cap \cdots \cap A_n)=(1-P(A_1))P(A_2)P(A_3) \cdots P(A_n)}\]したがって\[\mathrm{P(A_1^c \cap A_2\cap A_3\cap \cdots \cap A_n)=P(A_1^c)P(A_2)P(A_3) \cdots P(A_n)}\]となり,\((\ast)\)が証明できました(証明終)


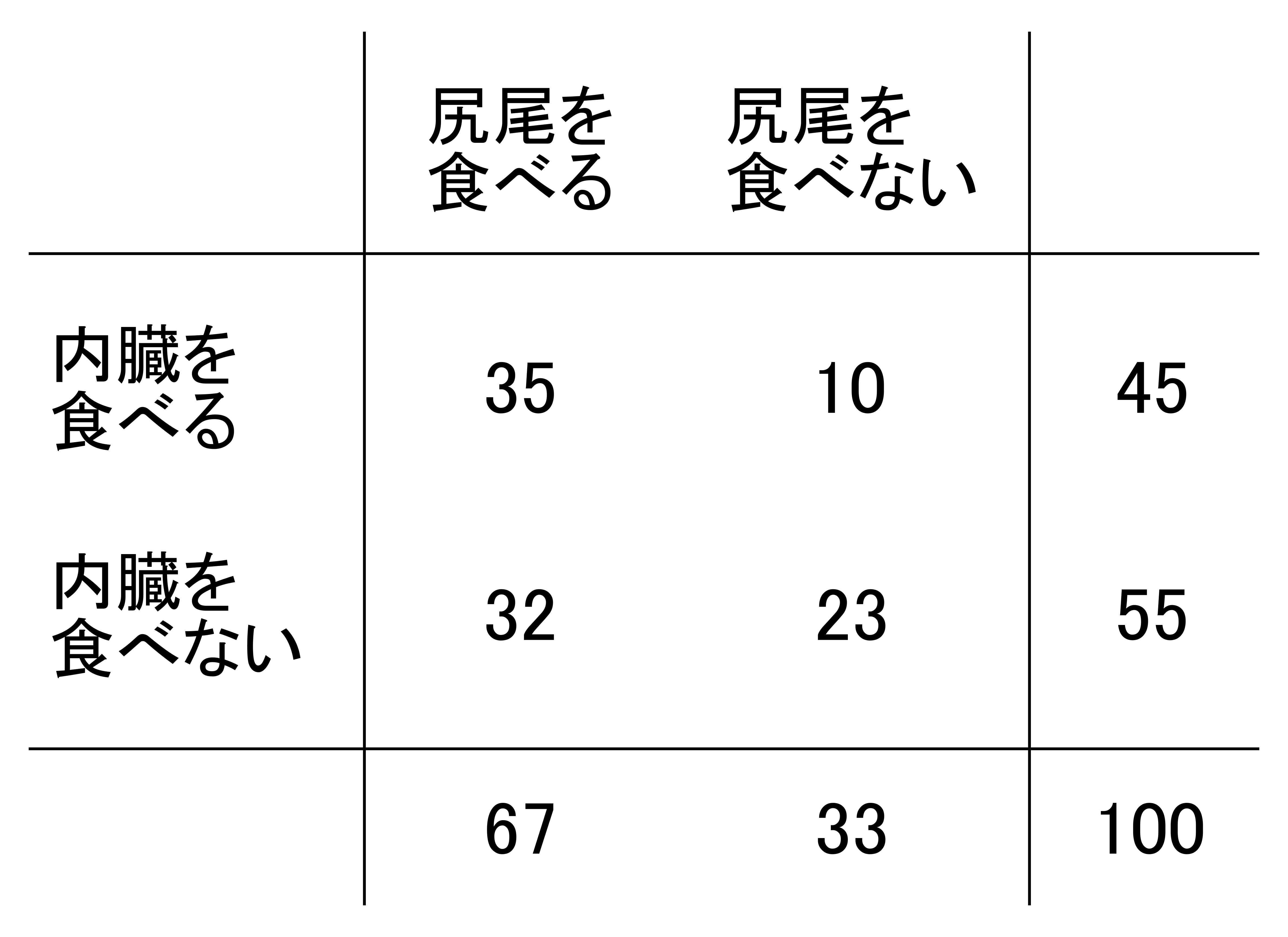 問題
問題