数学Ⅰの「集合と論理」を学んだ高校生にぜひ考えてもらいたい問題。
\(|x-a| < \epsilon \Longleftrightarrow a-\epsilon < x < a+ \epsilon\)で,この不等式において\(\epsilon\)は任意の正数,つまり正の数なら何入れても成り立つとすれば\(x=a\)である,換言すれば「幅をどんだけ小さくしても,その間に\(x\)が入るというのなら,その\(x\)って\(a\)だよね?」といっています。感覚的には正しそう?
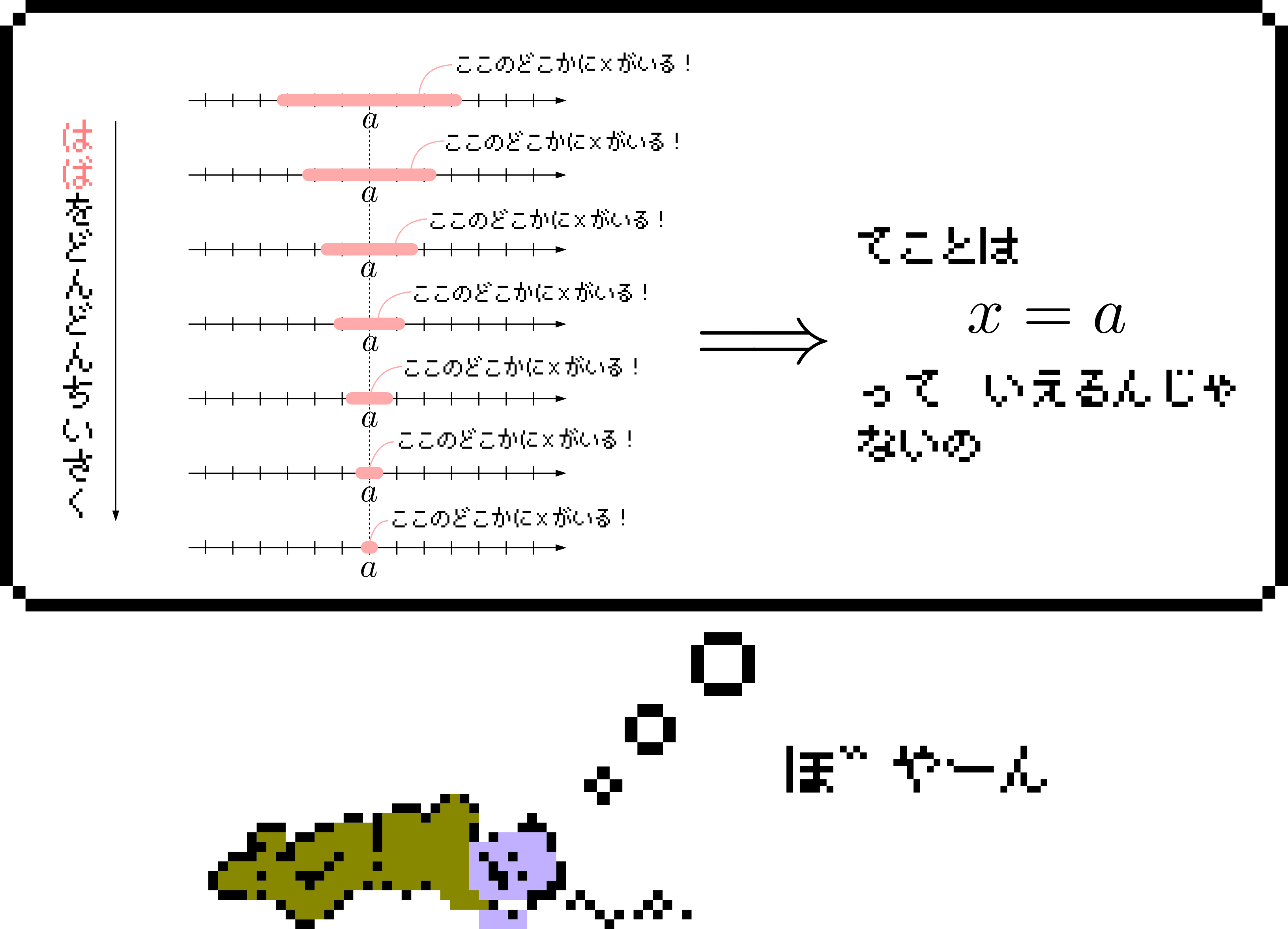
証明
示したいことは\[\forall \epsilon > 0 [|x-a| < \epsilon] \Longrightarrow x=a\]である.この命題を否定して\[\forall \epsilon > 0 [|x-a| < \epsilon] \land x \neq a\]と仮定する.このとき,\(|x-a| > 0\)であるから,\(0 < \epsilon^{\prime} < |x-a|\)を満たす\(\epsilon^{\prime}\)が存在する.\(\epsilon\)は任意だったので,この\(\epsilon^{\prime}\)をとることにする.すると,\(|x-a| < \epsilon^{\prime}<|x-a|\)より\(|x-a| < |x-a|\)となり矛盾する.したがって\[\forall \epsilon > 0 [|x-a| < \epsilon] \Longrightarrow x=a\]となる.
証明終
note:
\(\{a\}(\subset \mathbb{R})\)が閉集合であることの証明において,\(\{x|\forall \epsilon >0 [d(x,y) < \epsilon,y=a]\}=\{a\}\)を示す必要がありそこで使った。

