ななんだって!加法定理忘れた?!サイタコスモスどーのこーの?あーやめやめ。作りましょう。教科書には詳しく書いてありますが,それをここで繰り返してもつまらないのでちょっと違う証明を考えてみます。
証明
単位円周上に下図のような点\(\mathrm{P}\)があったとします.
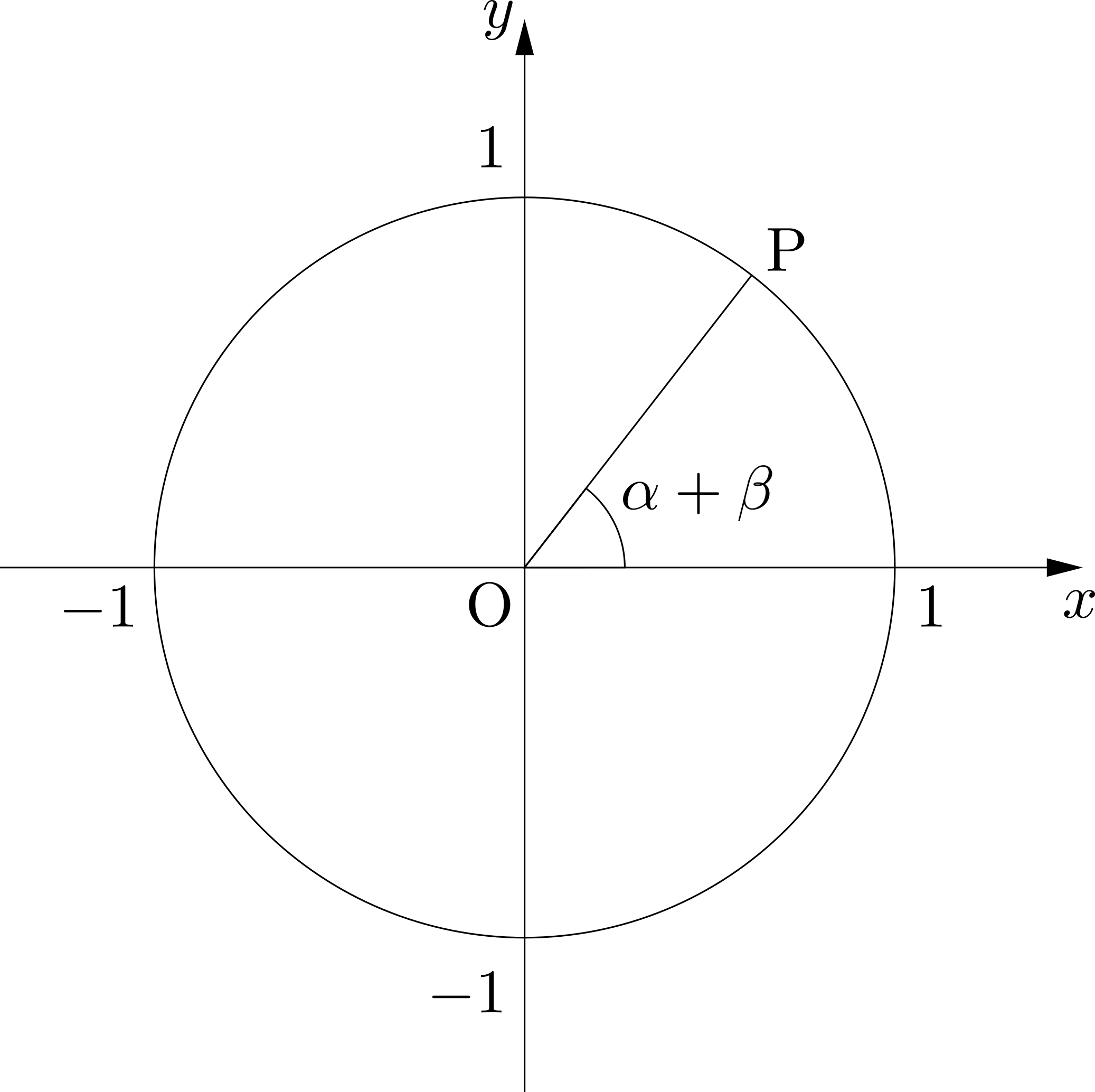
ここに,基本ベクトル\(\overrightarrow{e_1}=\left(\begin{array}{c} 1 \\ 0 \\ \end{array} \right),\overrightarrow{e_2}=\left(\begin{array}{c} 0 \\ 1 \\ \end{array} \right)\)をそれぞれ原点を中心に\(\alpha\)だけ回転させたベクトル\(\overrightarrow{\mathrm{OA}},\overrightarrow{\mathrm{OB}}\)を考え,図示します.\(\mathrm{A}(\cos\alpha,~\sin\alpha),~\mathrm{B}(\cos\left(\frac{\pi}{2}+\alpha\right),~\sin\left(\frac{\pi}{2}+\alpha\right))\)ですから,それらの成分は\[\overrightarrow{\mathrm{OA}}=\left(\begin{array}{c} \cos\alpha \\ \sin\alpha \\ \end{array} \right),\quad\overrightarrow{\mathrm{OB}}=\left(\begin{array}{c} \cos\left(\frac{\pi}{2}+\alpha\right) \\ \sin\left(\frac{\pi}{2}+\alpha\right) \\ \end{array} \right)=\left(\begin{array}{c} -\sin\alpha \\ \cos\alpha \\ \end{array} \right)\]です.
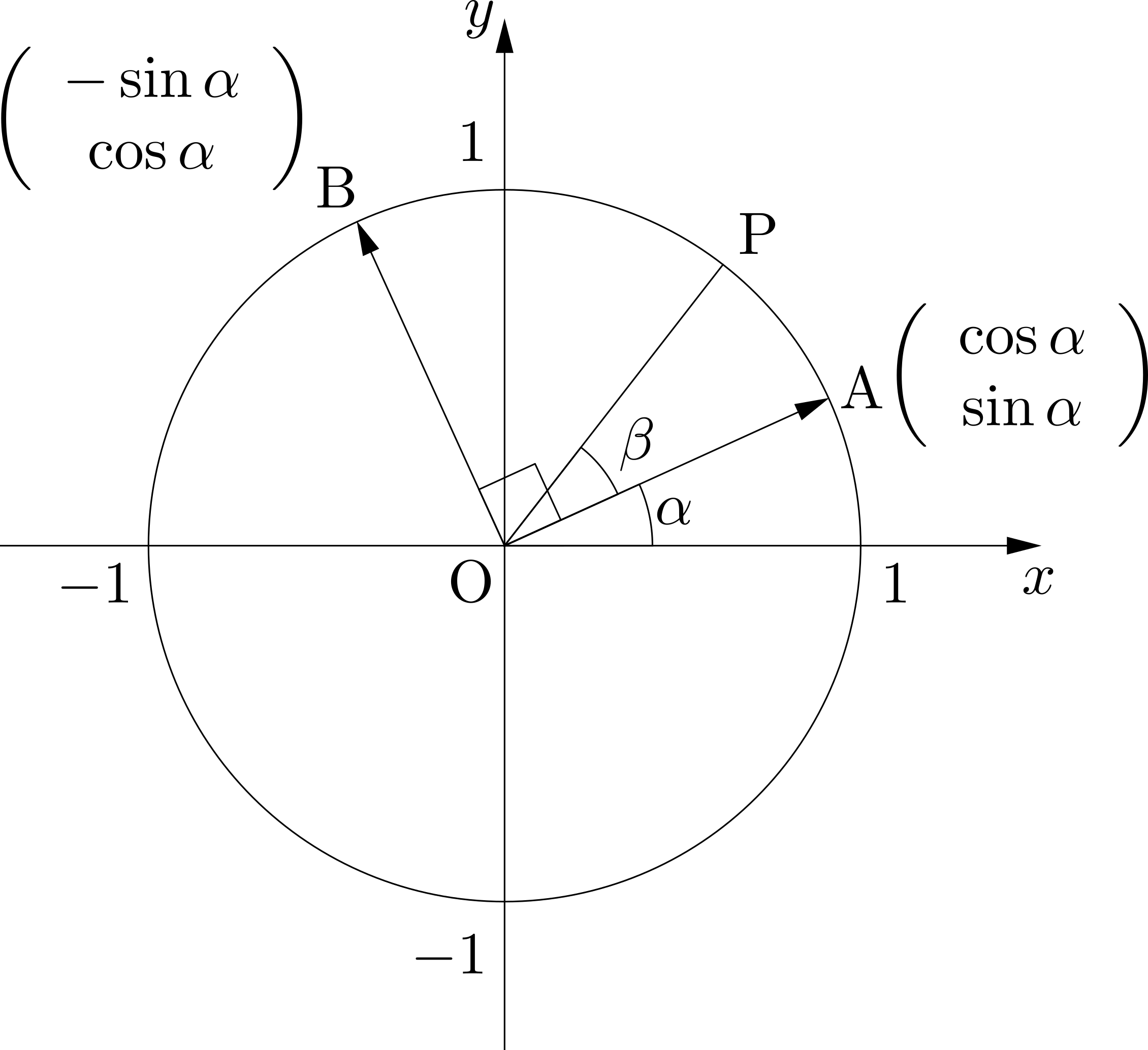
この\(\overrightarrow{\mathrm{OA}}\),\(\overrightarrow{\mathrm{OB}}\)を基底とする新たな座標系の下でこの点\(\mathrm{P}\)を捉え直します.この新座標系における図の点\(\mathrm{P}\)の座標は,\((\cos\beta,~\sin\beta)\),すなわち\[
\begin{align*}
\overrightarrow{\mathrm{OP}}
&=\cos\beta\overrightarrow{\mathrm{OA}}+\sin\beta\overrightarrow{\mathrm{OB}}\\
&=\cos\beta\left(\begin{array}{c} \cos\alpha \\ \sin\alpha \\ \end{array} \right)+\sin\beta\left(\begin{array}{c} -\sin\alpha \\ \cos\alpha \\ \end{array} \right)\\
&=\left(\begin{array}{c} \cos\alpha\cos\beta-\sin\alpha\sin\beta \\ \sin\alpha\cos\beta+\cos\alpha\sin\beta \\ \end{array} \right)
\end{align*}\]です.
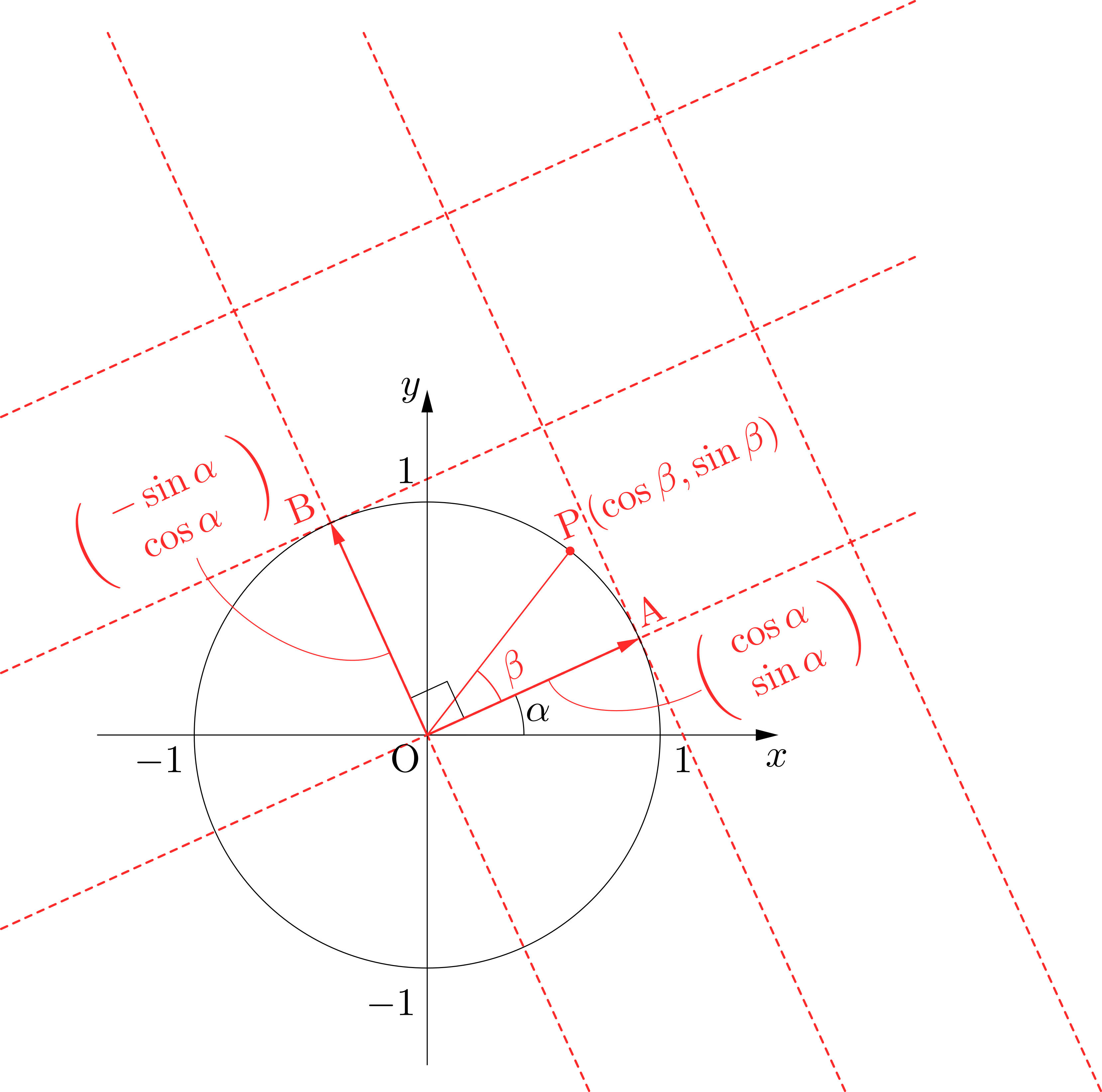
さらにこれは,
\begin{align*}
\overrightarrow{\mathrm{OP}}&=\left(\begin{array}{c} \cos\alpha\cos\beta-\sin\alpha\sin\beta \\ \sin\alpha\cos\beta+\cos\alpha\sin\beta \\ \end{array} \right)\\
&=(\cos\alpha\cos\beta-\sin\alpha\sin\beta)\left(\begin{array}{c} 1 \\ 0 \\ \end{array} \right)+(\sin\alpha\cos\beta+\cos\alpha\sin\beta)\left(\begin{array}{c} 0 \\ 1 \\ \end{array} \right)\\
&=(\cos\alpha\cos\beta-\sin\alpha\sin\beta)\overrightarrow{e_1}+(\sin\alpha\cos\beta+\cos\alpha\sin\beta)\overrightarrow{e_2}
\end{align*}
これは,点\(\mathrm{P}\)が,\(\overrightarrow{e_1},\overrightarrow{e_2}\)を基底とする(いつもの)座標系においてその座標が\[(\cos\alpha\cos\beta-\sin\alpha\sin\beta,\sin\alpha\cos\beta+\cos\alpha\sin\beta)\tag{1}\]であることを示しています.
他方,\(\overrightarrow{e_1},\overrightarrow{e_2}\)を基底とする座標系における点\(\mathrm{P}\)の座標は\begin{align*}\overrightarrow{\mathrm{OP}}=\left(\begin{array}{c} \cos(\alpha+\beta) \\ \sin(\alpha+\beta) \\ \end{array} \right)=&\cos(\alpha+\beta)\left(\begin{array}{c} 1 \\ 0 \\ \end{array} \right)+\sin(\alpha+\beta)\left(\begin{array}{c} 1 \\ 0 \\ \end{array} \right)\\ =& \cos(\alpha+\beta)\overrightarrow{e_1}+\sin(\alpha+\beta)\overrightarrow{e_2}\end{align*}より\[(\cos(\alpha+\beta),\sin(\alpha+\beta))\tag{2}\]であったから,\((1),(2)\)によって
\begin{eqnarray}
\begin{cases}
\cos(\alpha+\beta) = \cos\alpha\cos\beta-\sin\alpha\sin\beta & \\
\sin(\alpha+\beta) = \sin\alpha\cos\beta+\cos\alpha\sin\beta &
\end{cases}
\end{eqnarray}
が得られます.
証明終
説明しながらの記述なので面倒くさく見えるかもしれませんが,実際やってみると計算らしい計算なしにすぐに作れます。おすすめ。ちなみに\(\alpha-\beta\)の場合については上で得られた式の\(\beta\)を\(-\beta\)に変えれ直ちに手に入ります。(関連:斜交座標)
サイタコスモスコスモスサイタって覚え方を初めて聞いたとき「コスモスサイタサイタコスモスでも通じるじゃん,覚え方として全く意味なくね…?」と思ったし今でもそう思う。

