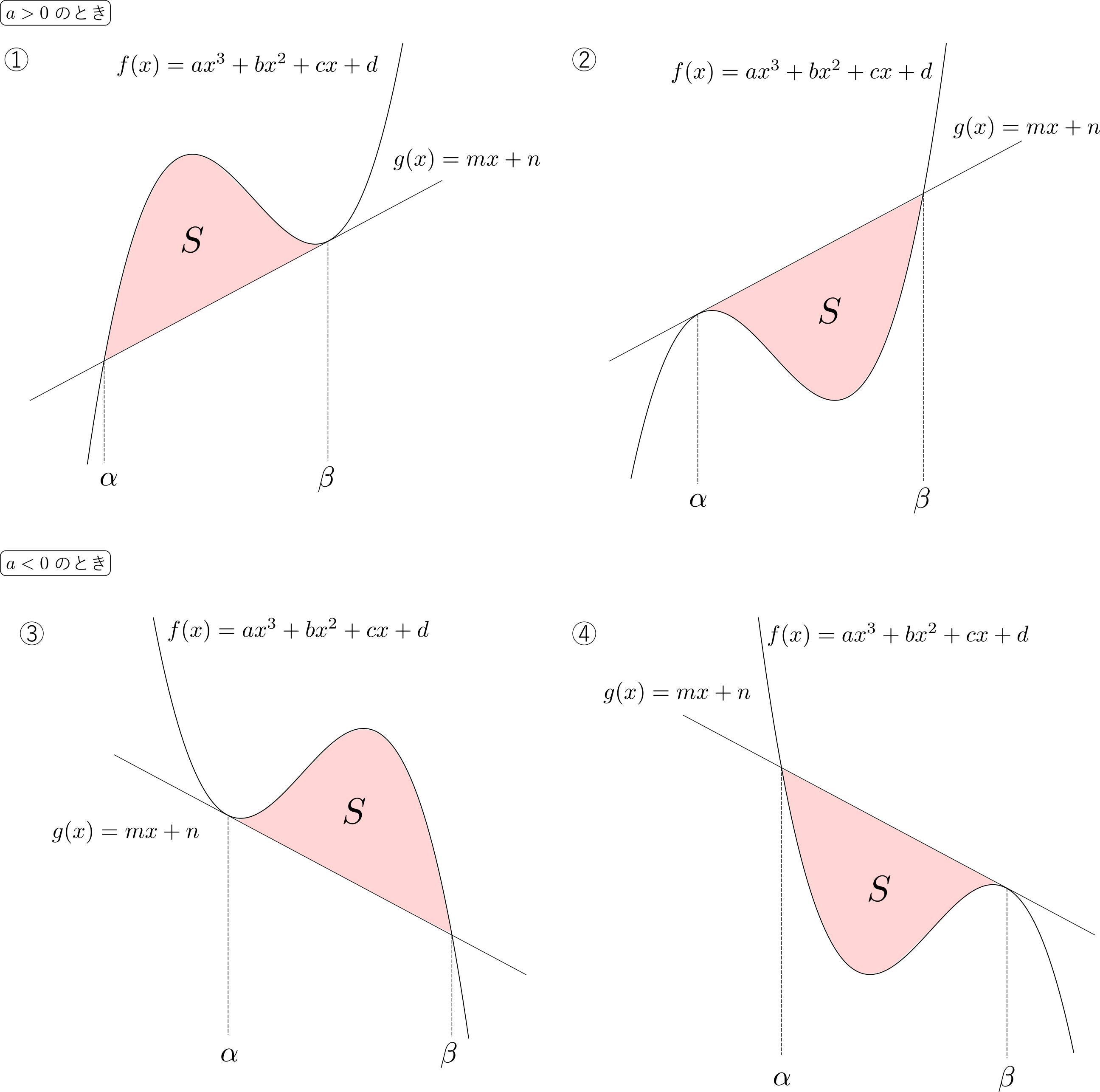
 上の曲線と直線で囲まれる部分の面積\(S\)は,いずれの場合も\[S = \frac{|a|(\beta-\alpha)^4}{12}\]で表される.
上の曲線と直線で囲まれる部分の面積\(S\)は,いずれの場合も\[S = \frac{|a|(\beta-\alpha)^4}{12}\]で表される.証明
(① \(a>0\)で\(f(x)\)が上の場合)
被積分関数\(f(x)-g(x)\)がどんな関数になるかを考える.これは,
-
-
- \(3\)次式で,
- 次数が一番大きい項の係数は\(a\)で,
- \(x=\alpha\)で交わり\(x=\beta\)で接する,すなわち\(f(x)-g(x)=0\)を解いて得られる\(2\)つの解が\(\alpha,\beta,\beta\)である
-
ことに着目すると,\[g(x)-f(x) = a(x-\alpha)(x-\beta)^2\]とかける.したがって求める部分の面積は
\begin{align*}
&\displaystyle \int_{\alpha}^{\beta} a(x-\alpha)(x-\beta)^2 dx \\
=~&\displaystyle a\int_{\alpha}^{\beta} (x-\alpha)(x-\beta)^2 dx\\
=~&\frac{a(\beta-\alpha)^4}{12}\tag{2}\\
=~&\frac{|a|(\beta-\alpha)^4}{12}
\end{align*}
(② \(a>0\)で\(f(x)\)が下の場合)
上と同様に考え,
\begin{align*}
&\displaystyle \int_{\alpha}^{\beta} \{g(x)-f(x)\} dx \\
=~&\displaystyle \int_{\alpha}^{\beta} -a(x-\alpha)^2(x-\beta) dx \\
=~&\displaystyle -a\int_{\alpha}^{\beta} (x-\beta)(x-\alpha)^2 dx\\
=~&\displaystyle a\int_{\beta}^{\alpha} (x-\beta)(x-\alpha)^2 dx\\
=~&\frac{a(\beta-\alpha)^4}{12}\tag{2}\\
=~&\frac{|a|(\beta-\alpha)^4}{12}
\end{align*}
(③ \(a<0\)で\(f(x)\)が上の場合)
\begin{align*}
&\displaystyle \int_{\alpha}^{\beta} \{f(x)-g(x)\} dx \\
=~&\displaystyle \int_{\alpha}^{\beta} a(x-\alpha)^2(x-\beta) dx \\
=~&\displaystyle a\int_{\alpha}^{\beta} (x-\alpha)^2(x-\beta) dx\\
=~&\displaystyle -a\int_{\beta}^{\alpha} (x-\beta)(x-\alpha)^2 dx\\
=~&\frac{-a(\beta-\alpha)^4}{12}\tag{2}\\
=~&\frac{|a|(\beta-\alpha)^4}{12}
\end{align*}
(④ \(a<0\)で\(f(x)\)が下の場合)
\begin{align*}
&\displaystyle \int_{\alpha}^{\beta} \{g(x)-f(x)\} dx \\
=~&\displaystyle \int_{\alpha}^{\beta} -a(x-\alpha)(x-\beta)^2 dx \\
=~&\displaystyle -a\int_{\alpha}^{\beta} (x-\alpha)(x-\beta)^2 dx\\
=~&\frac{-a(\beta-\alpha)^4}{12}\tag{2}\\
=~&\frac{|a|(\beta-\alpha)^4}{12}
\end{align*}
以上により,いずれの場合も面積\(S\)は\[\frac{|a|(\beta-\alpha)^3}{6}\]で表されることになる.
証明終
やはり,交点\(\alpha,\beta\)と\(a\)さえ分かってしまえば面積は求まってしまいます。\((2)\)はここの公式によります.

