\(\overrightarrow{a}\times(\overrightarrow{b}+\overrightarrow{c})=\overrightarrow{a}\times\overrightarrow{b}+\overrightarrow{a}\times\overrightarrow{c}\)を証明します。
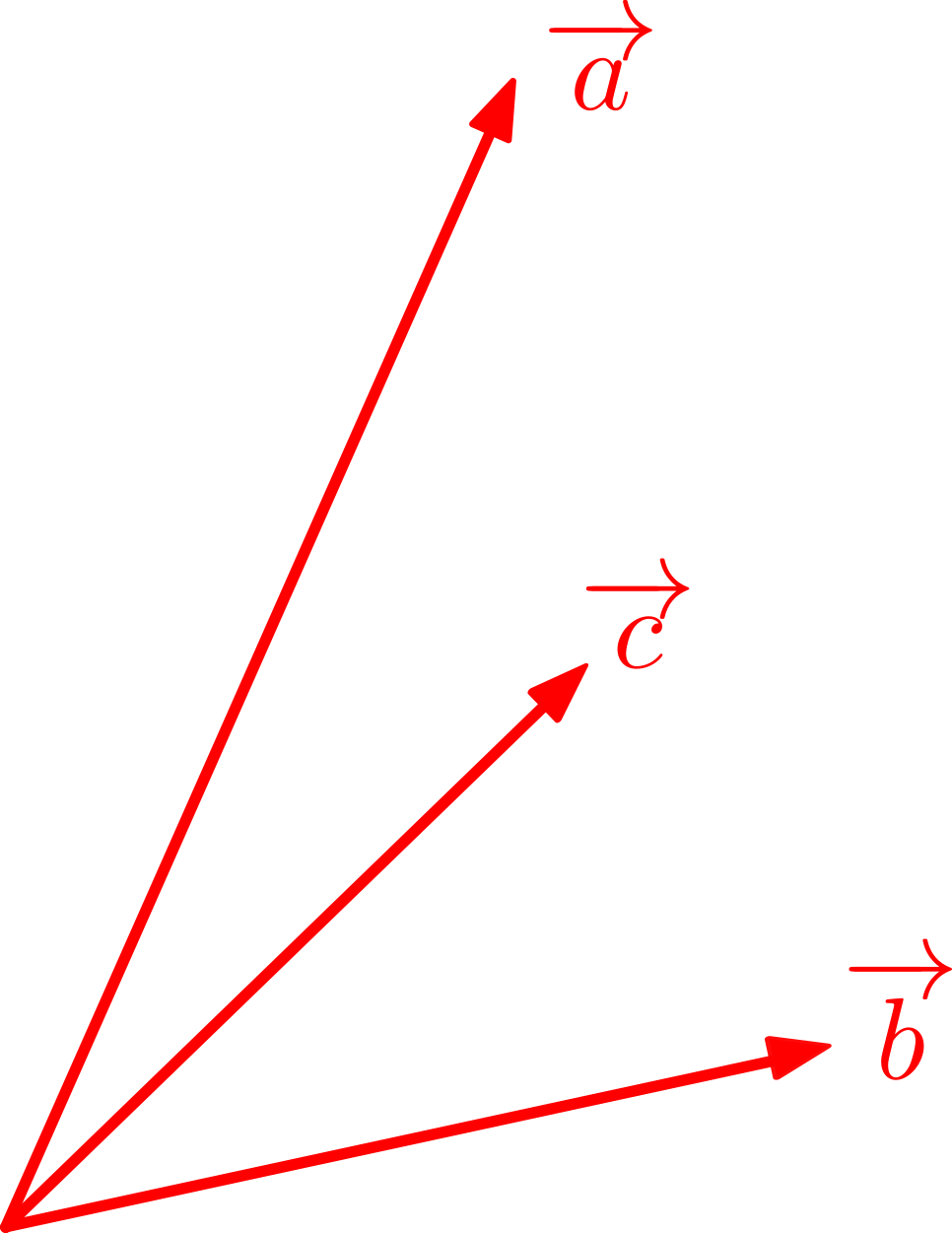
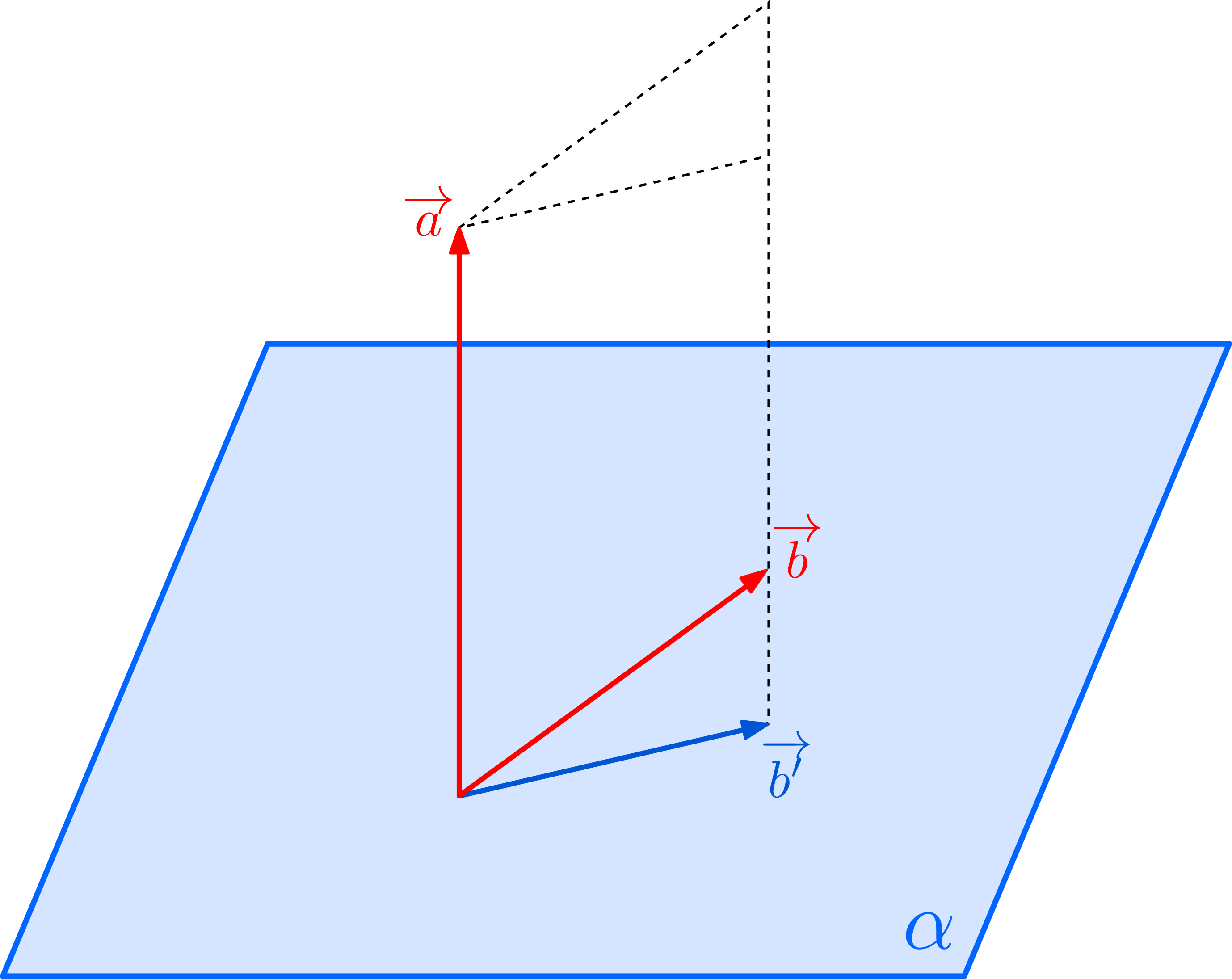
図のように,空間上に\(\overrightarrow{a},\overrightarrow{b},\overrightarrow{c}\)があったとしましょう。
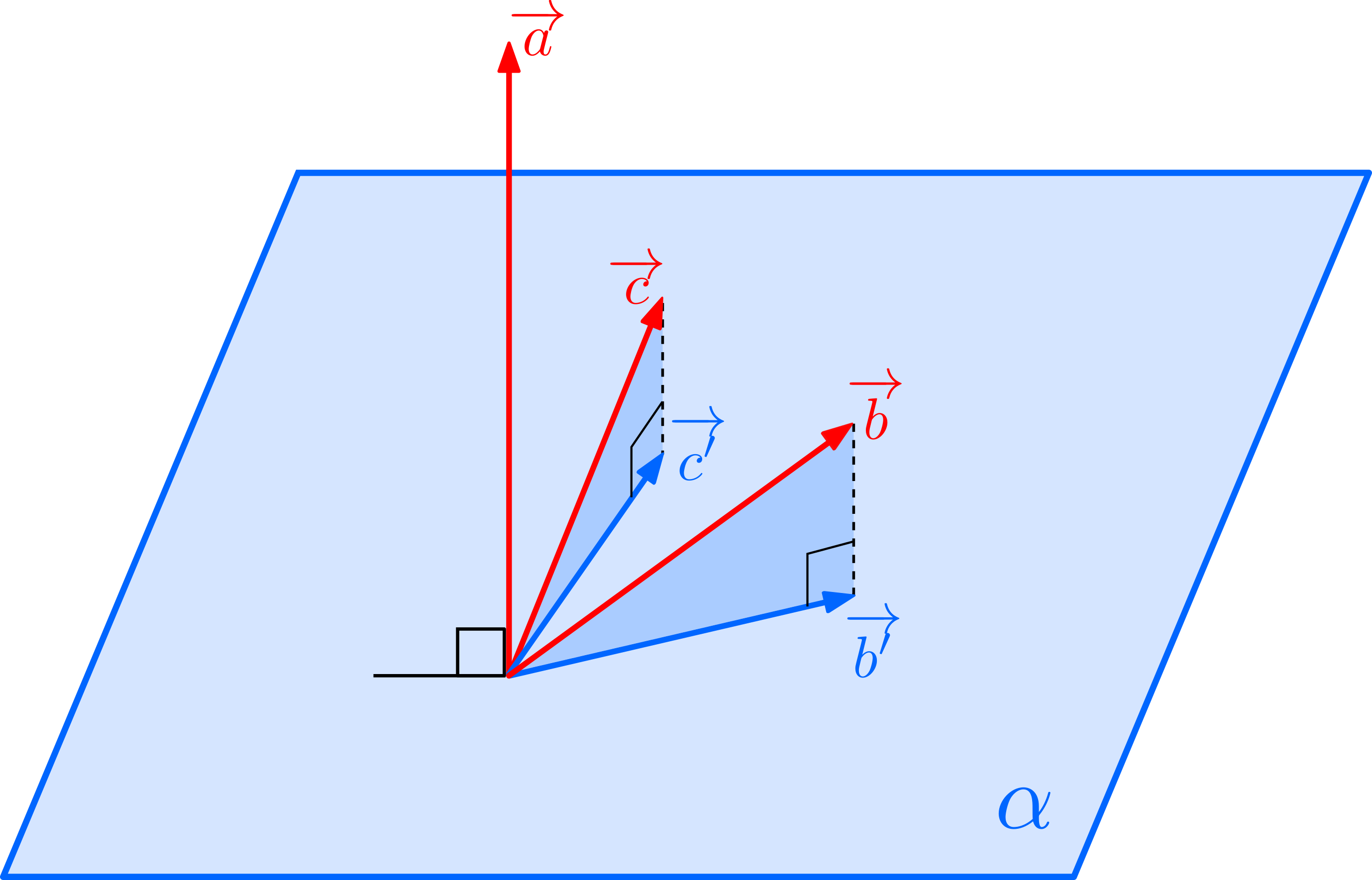
\(\overrightarrow{a}\)の始点を通り,\(\overrightarrow{a}\)に垂直な平面を\(\alpha\)とし,\(\overrightarrow{b},\overrightarrow{c}\)からその平面\(\alpha\)への正射影ベクトルをそれぞれ\(\overrightarrow{b^{\prime}},\overrightarrow{c^{\prime}}\)とおきます。
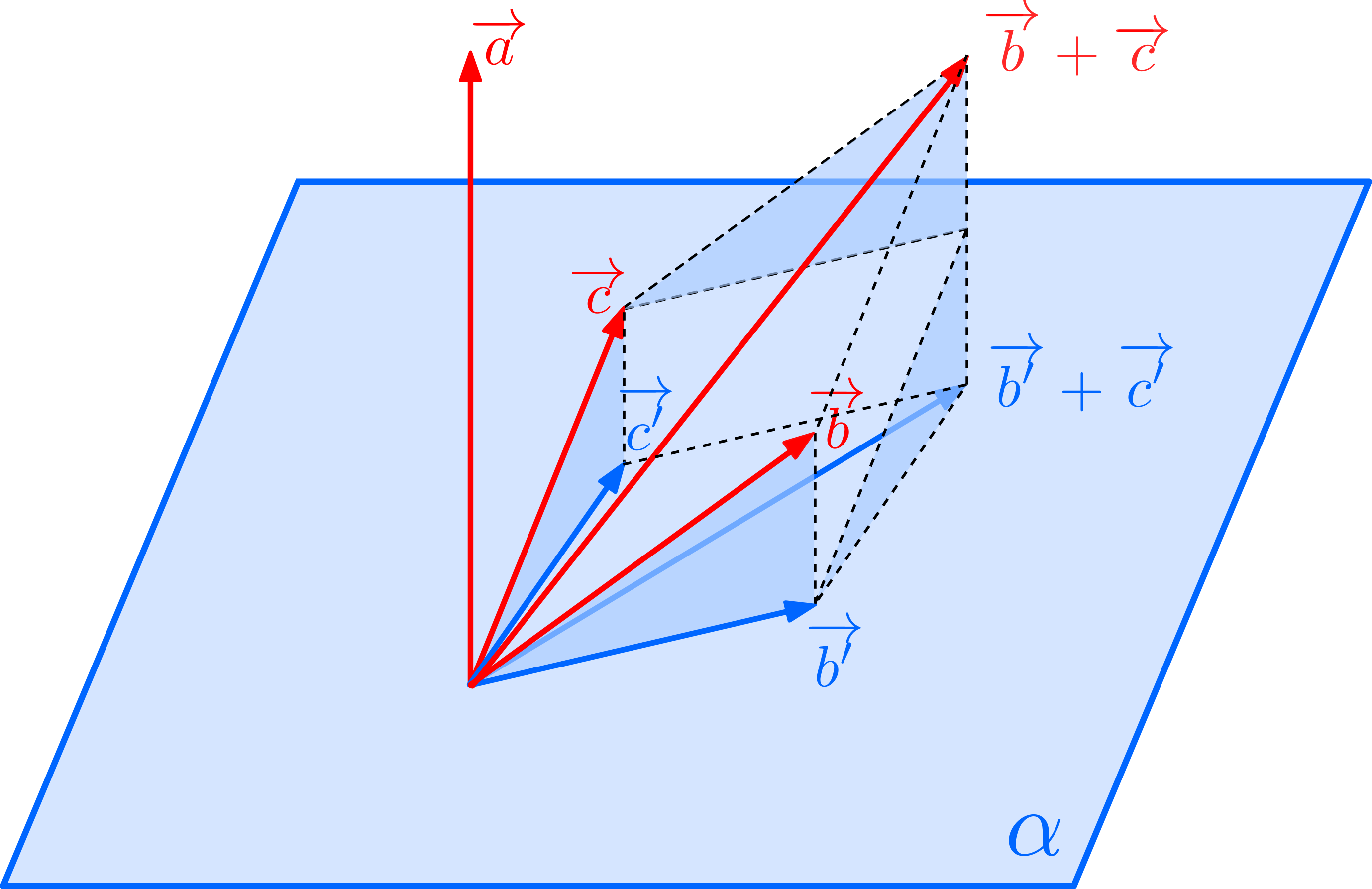
このとき,下図のような位置関係があることに注意しておきます。
図を動かしてイメージしてみてください(右クリックを押しながらドラッグすると動きます)。
さて,このとき,\begin{align*}
\overrightarrow{a}\times(\overrightarrow{b}+\overrightarrow{c})=&\overrightarrow{a}\times(\overrightarrow{b^{\prime}}+\overrightarrow{c^{\prime}})\tag{1}\\
=&\overrightarrow{a}\times \overrightarrow{b^{\prime}}+\overrightarrow{a}\times \overrightarrow{c^{\prime}}\tag{2}\\
=&\overrightarrow{a}\times \overrightarrow{b}+\overrightarrow{a}\times \overrightarrow{c}\tag{3}
\end{align*}が言えます。順にみていきます。
 \((1)\)について:
\((1)\)について:
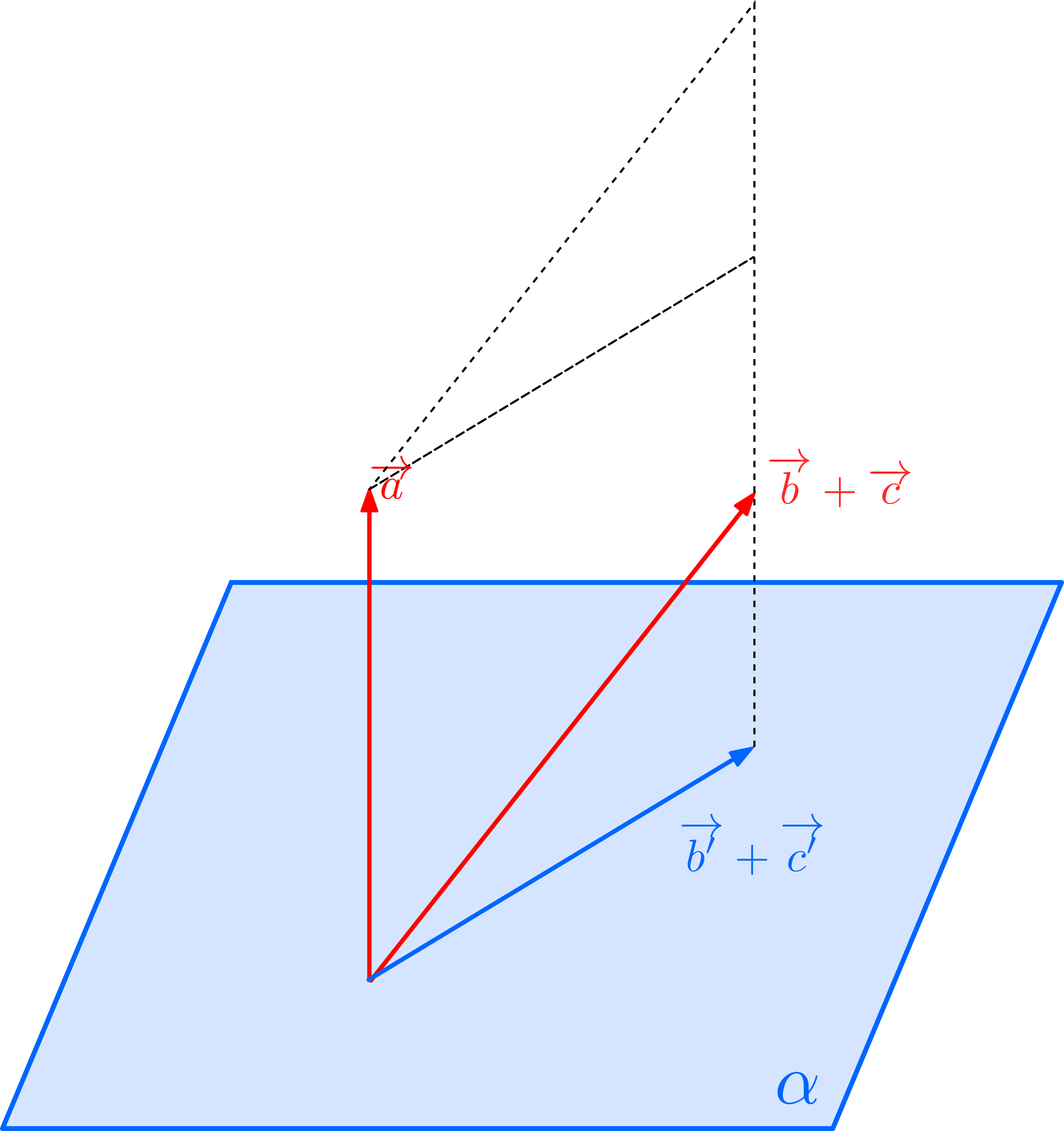
\(\overrightarrow{a},\overrightarrow{b}+\overrightarrow{c},\overrightarrow{b^{\prime}}+\overrightarrow{c^{\prime}}\)は同一平面上にありますから,まず\(\overrightarrow{a}\times(\overrightarrow{b}+\overrightarrow{c})\)と\(\overrightarrow{a}\times(\overrightarrow{b^{\prime}}+\overrightarrow{c^{\prime}})\)の向きは同じであることが分かります。そして,\(\overrightarrow{a}\)と\(\overrightarrow{b}+\overrightarrow{c}\)が作る平行四辺形の面積と,\(\overrightarrow{a}\)と\(\overrightarrow{b^{\prime}}+\overrightarrow{c^{\prime}}\)が作る平行四辺形の面積は等しいので(等積変形),\(\overrightarrow{a}\times(\overrightarrow{b}+\overrightarrow{c})\)と\(\overrightarrow{a}\times(\overrightarrow{b^{\prime}}+\overrightarrow{c^{\prime}})\)の大きさも等しい。したがって\[\overrightarrow{a}\times(\overrightarrow{b}+\overrightarrow{c})=\overrightarrow{a}\times(\overrightarrow{b^{\prime}}+\overrightarrow{c^{\prime}})\tag{1}\]です。
\((2)\)について:
\(\overrightarrow{a}\times \overrightarrow{b^{\prime}},\overrightarrow{a}\times \overrightarrow{c^{\prime}},\overrightarrow{a}\times(\overrightarrow{b^{\prime}}+\overrightarrow{c^{\prime}})\)の向きはどれも\(\overrightarrow{a}\)を軸に\(90^{\circ}\)回転させた向きになります。そして大きさは(どれも\(\overrightarrow{a}\)と直交していることに注意すれば)それぞれ\(|\overrightarrow{a}||\overrightarrow{b^{\prime}}|,|\overrightarrow{a}||\overrightarrow{c^{\prime}}|,|\overrightarrow{a}||\overrightarrow{b^{\prime}}+\overrightarrow{c^{\prime}}|\),すなわちどれも自分の大きさを\(|\overrightarrow{a}|\)倍したものです。
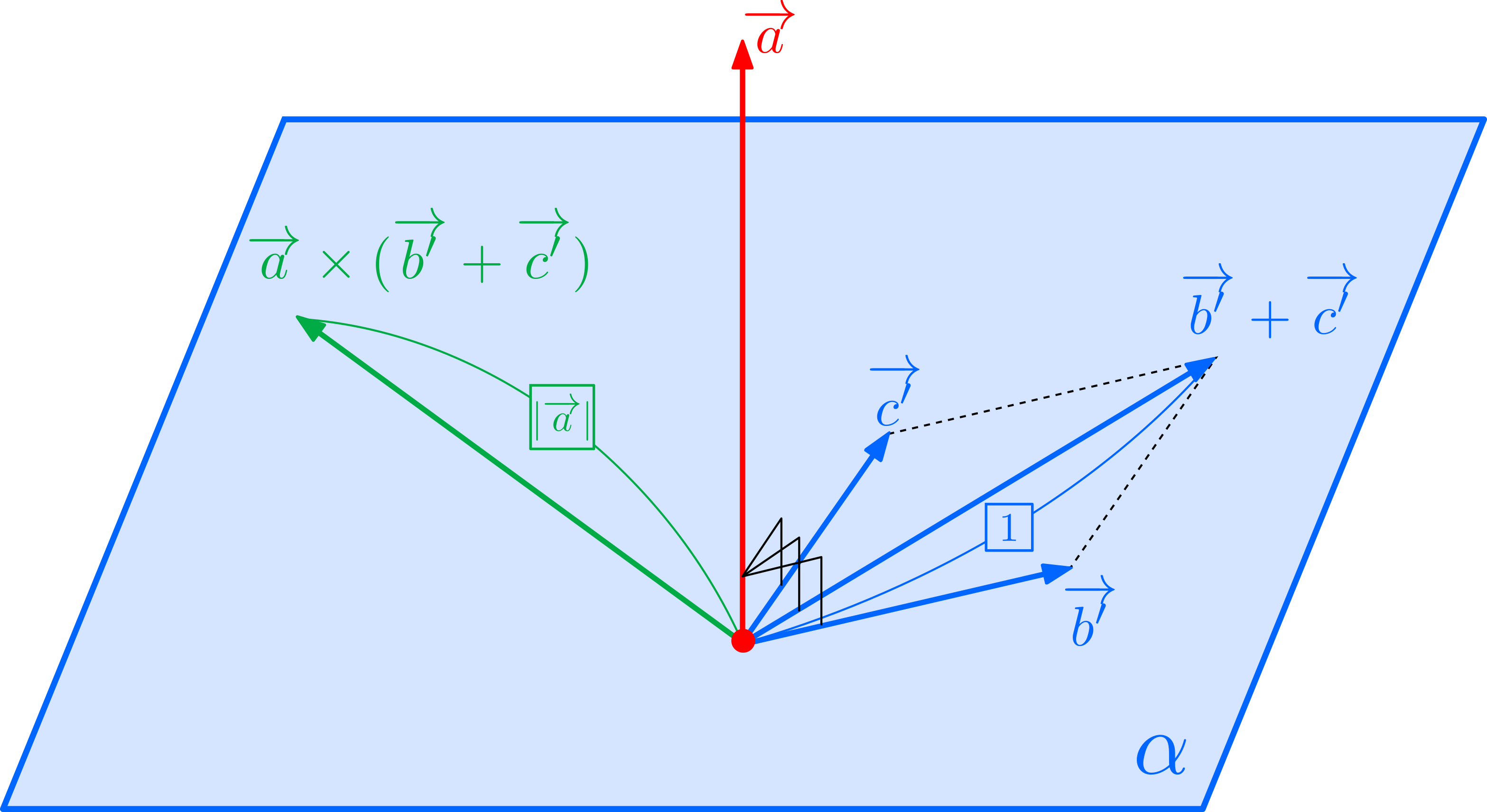
(上の図は見やすさのため\(\overrightarrow{a}\times(\overrightarrow{b^{\prime}}+\overrightarrow{c^{\prime}})\)だけ図示)これを,真上から見たものが下の図がです。
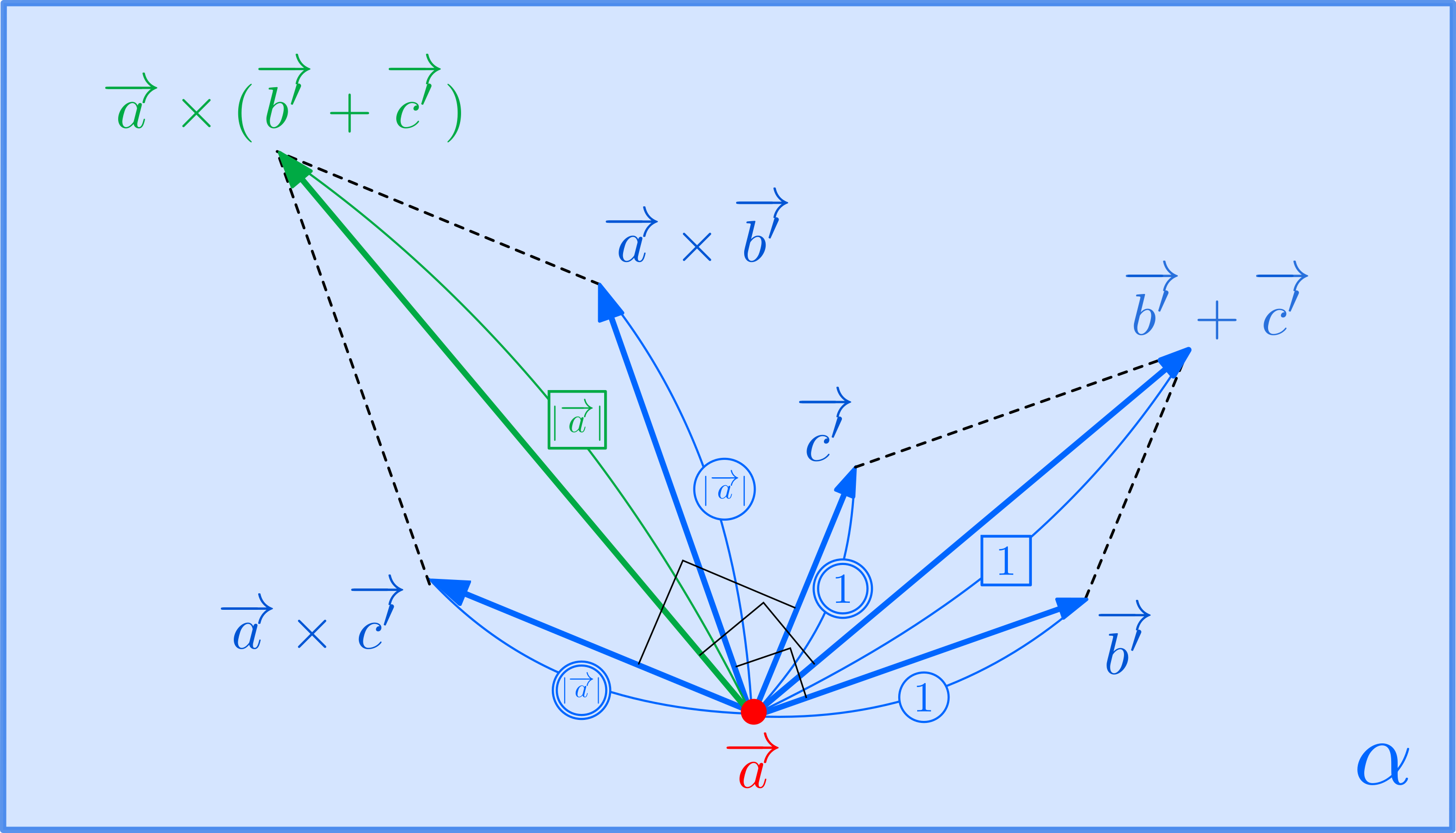
この図から,\[\overrightarrow{a}\times(\overrightarrow{b^{\prime}}+\overrightarrow{c^{\prime}})=\overrightarrow{a}\times\overrightarrow{b^{\prime}}+\overrightarrow{a}\times\overrightarrow{c^{\prime}}\tag{2}\]であることが分かります。
 \((3)\)について:
\((3)\)について:
\(\overrightarrow{a},\overrightarrow{b},\overrightarrow{b^{\prime}}\)は同一平面上にありますから,まず\(\overrightarrow{a}\times\overrightarrow{b}\)と\(\overrightarrow{a}\times\overrightarrow{b^{\prime}}\)の向きは同じであることが分かります。そして,\(\overrightarrow{a}\)と\(\overrightarrow{b}\)が作る平行四辺形の面積と,\(\overrightarrow{a}\)と\(\overrightarrow{b^{\prime}}\)が作る平行四辺形の面積は等しいので(等積変形),\(\overrightarrow{a}\times \overrightarrow{b}\)と\(\overrightarrow{a}\times\overrightarrow{b^{\prime}}\)の大きさも等しい。したがって\[\overrightarrow{a}\times \overrightarrow{b}=\overrightarrow{a}\times \overrightarrow{b^{\prime}}\tag{3}\]です。
\(\overrightarrow{a}\times \overrightarrow{c}=\overrightarrow{a}\times \overrightarrow{c^{\prime}}\)も同様です。
以上により証明が完了しました。

