投稿者: shotasasaki

投稿日:

上限の定義

\(A\)を集合\(S\)の空でない部分集合とします。

上限の定義\(A\)が上に有界であるとき，もし\(A\)の上界のうちに最小元\(a\)があるならば，\(a\)を\(A\)の上限といい，\[\sup A=a\]と表す．

この定義を詳しく見ると，上限とは，

\((1)\) \(a\)は\(A\)の上界である
\((2)\) \(a\)は\(A\)の上界の最小元である

の2つで特徴付けられていることがわかります。これらを論理記号を用いて記述してみると
\begin{align*}
&\forall x\in A[x \leq a]\tag{1}\\
&\forall x\in A[x \leq a^{\prime}]\Longrightarrow a\leq a^{\prime}\tag{2}
\end{align*}そこで，\((2)\)を変形してみます。すると
\begin{align*}
&\forall x\in A[x \leq a^{\prime}]\Longrightarrow a\leq a^{\prime}\tag{2}\\
\Longleftrightarrow~&\overline{\forall x\in A[x \leq a^{\prime}]} \lor a\leq a^{\prime}\\
\Longleftrightarrow~&a\leq a^{\prime} \lor \overline{\forall x\in A[x \leq a^{\prime}]}\\
\Longleftrightarrow~&\overline{a > a^{\prime}} \lor \exists x\in A[x > a^{\prime}]\\
\Longleftrightarrow~& a > a^{\prime} \Longrightarrow \exists x\in A[x > a^{\prime}]\tag{2′}
\end{align*}つまり，\((2′)\)は「\(a\)より少しでも小さい\(a^{\prime}\)を持ってくると，その\(a^{\prime}\)よりも大きい\(A\)の元が存在してしまう」すなわち「\(a\)より少しでも小さい\(a^{\prime}\)を持ってくると，それはもはや上界ではない」ということになります。したがって上の\((1),(2)\)は

\((1)\) \(a\)は\(A\)の上界である
\((2′)\) \(a^{\prime}\)を\(a^{\prime} < a\)を満たす\(S\)の任意の元とすれば，\(a^{\prime}\)は\(A\)の上界ではない

と言い換えらえれることになります。

\(*\)\(*\)\(*\)

\((2)\)と書かれている本と\((2′)\)と書かれている本があって気になっていたので整理してみました。

投稿日:

「存在することを示せ」と言われたら　

（数学A，数学B）

「ツチノコの存在を証明しろ」と言われたら，どうすればいいか。
…それは簡単，ツチノコを捕まえて連れてくればOK！

ここで，数学Aの「整数の性質」で登場した「整数の割り算」について見てみます。

一般に，次のことが成り立つ。

整数\(a\)と正の整数\(b\)について\[a=qb+r,~0\leq r < b\]となる整数\(q,r\)はただ\(1\)通りに定まる。

『高等学校 数学A』数研出版

 
「定まる」とは要は「存在する」ということですが，いずれにせよ初めて学んだときは感覚的に当たり前すぎて疑問にすら思わなかったと思います。しかし，いざこれを証明しろと言われたらどうしたらいいでしょう…？

ずばり，実際にもってこよう！（以下では簡単のために\(a\geq 0\)とし，また一意性の部分はカットします）

\(a,b\)を\(a \geq 0,b>0\)を満たす整数とする．このとき，
\[a=qb+r,~0\leq r < b\tag{\(\ast\)}\]を満たす整数\(q,r\)が存在することを示せ．

証明

\(b(>0)\)を固定して，任意の\(a(\geq 0)\)について主張が成り立つことが示せればよい．

\(a < b\)であるとき：
\(q=0,r=a\)とすればよい．

\((0 <)b \leq a\)であるとき：
数学的帰納法で示す．\(a\)より小さい非負の整数で主張が成り立つとする．\(b>0\)より\(b \leq a \Leftrightarrow 0 \leq a-b (< a)\)であるから，\(a-b\)は\(a\)より小さい非負の整数である．したがって仮定により，\begin{align*}
&\exists q^{\prime},r^{\prime}\in \mathbb{Z}[a-b = q^{\prime}b+r^{\prime},0 \leq r^{\prime} \leq b]\\
\Longleftrightarrow~&\exists q^{\prime},r^{\prime}\in \mathbb{Z}[a = (q^{\prime}+1)b+r^{\prime},0 \leq r^{\prime} \leq b]
\end{align*}よって\((\ast)\)を満たす\(q,r\)として\(q=q^{\prime}+1,~r=r^{\prime}\)ととればよい．
これで，\(a\)より小さい非負の整数で主張が成り立てば，\(a\)でも主張が成り立つことが分かった．
\(a=0\)のときは，\(q=0,r=0\)とすればよい．

以上により任意の\(a(\geq 0)\)に対して\((\ast)\)を満たす\(q,r \in \mathbb{Z}\)が存在することが示せた．

証明終

現物もってくれば文句ないだろっていう。

こんなところで数学Bで学んだ（学ぶ）数学的帰納法が登場するのも面白いですね。しかも直前の番号のみを仮定する教科書の定番タイプではなく，直前以前の番号すべてを仮定するタイプの帰納法です。

パズルみたいな学校数学もまあまあ面白いけど，個人的にはこういう緻密な調査の方がすきだなあ。点数にならないけど。

 

投稿日:

加法定理の証明

ななんだって！加法定理忘れた？！サイタコスモスどーのこーの？あーやめやめ。作りましょう。教科書には詳しく書いてありますが，それをここで繰り返してもつまらないのでちょっと違う証明を考えてみます。

加法定理\[\sin(\alpha \pm\beta)=\sin\alpha \cos\beta \pm \cos\alpha \sin\beta\]\[\cos(\alpha \pm \beta)=\cos\alpha \cos\beta \mp \sin\alpha \sin\beta\]

証明

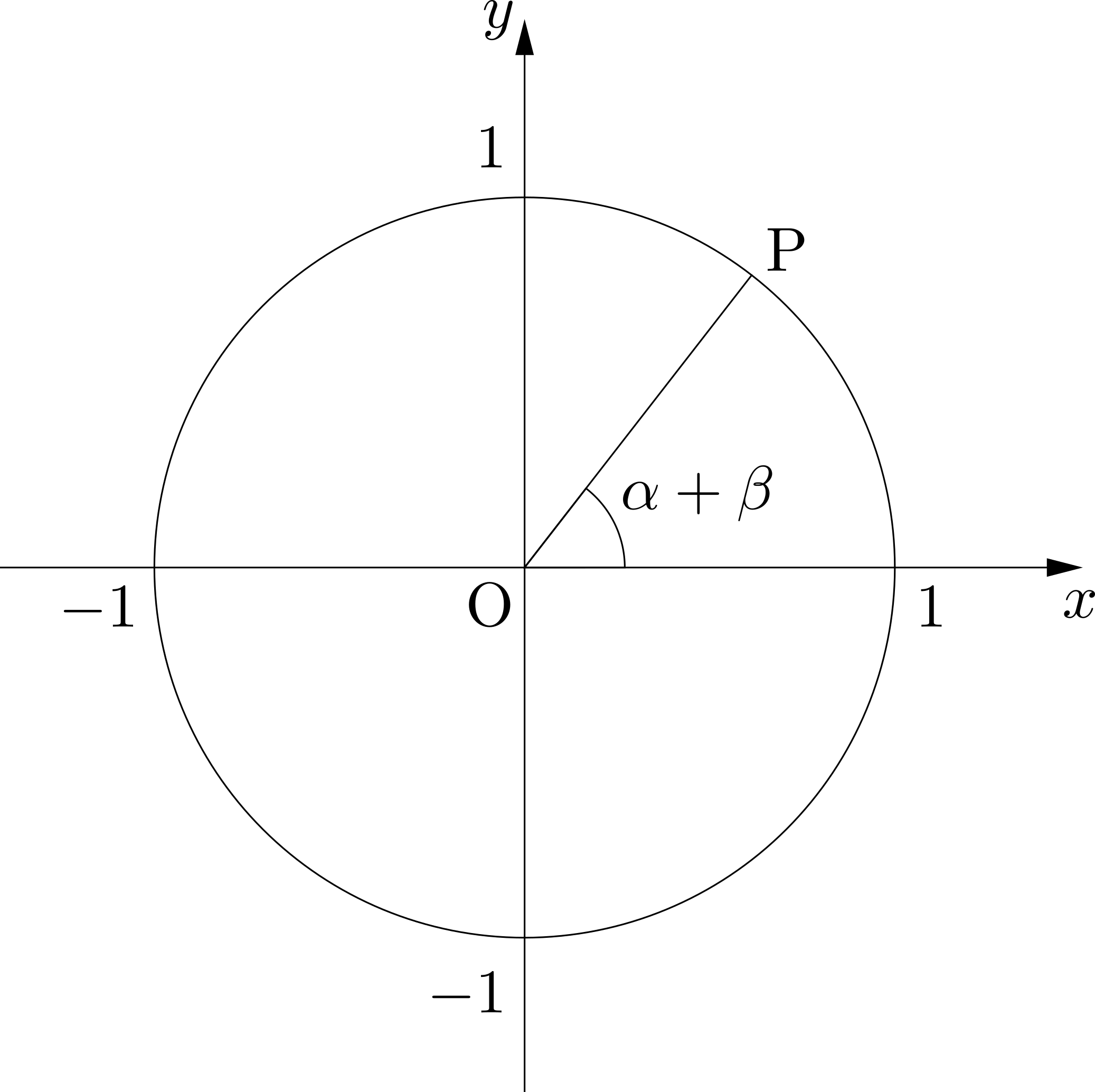
単位円周上に下図のような点\(\mathrm{P}\)があったとします．

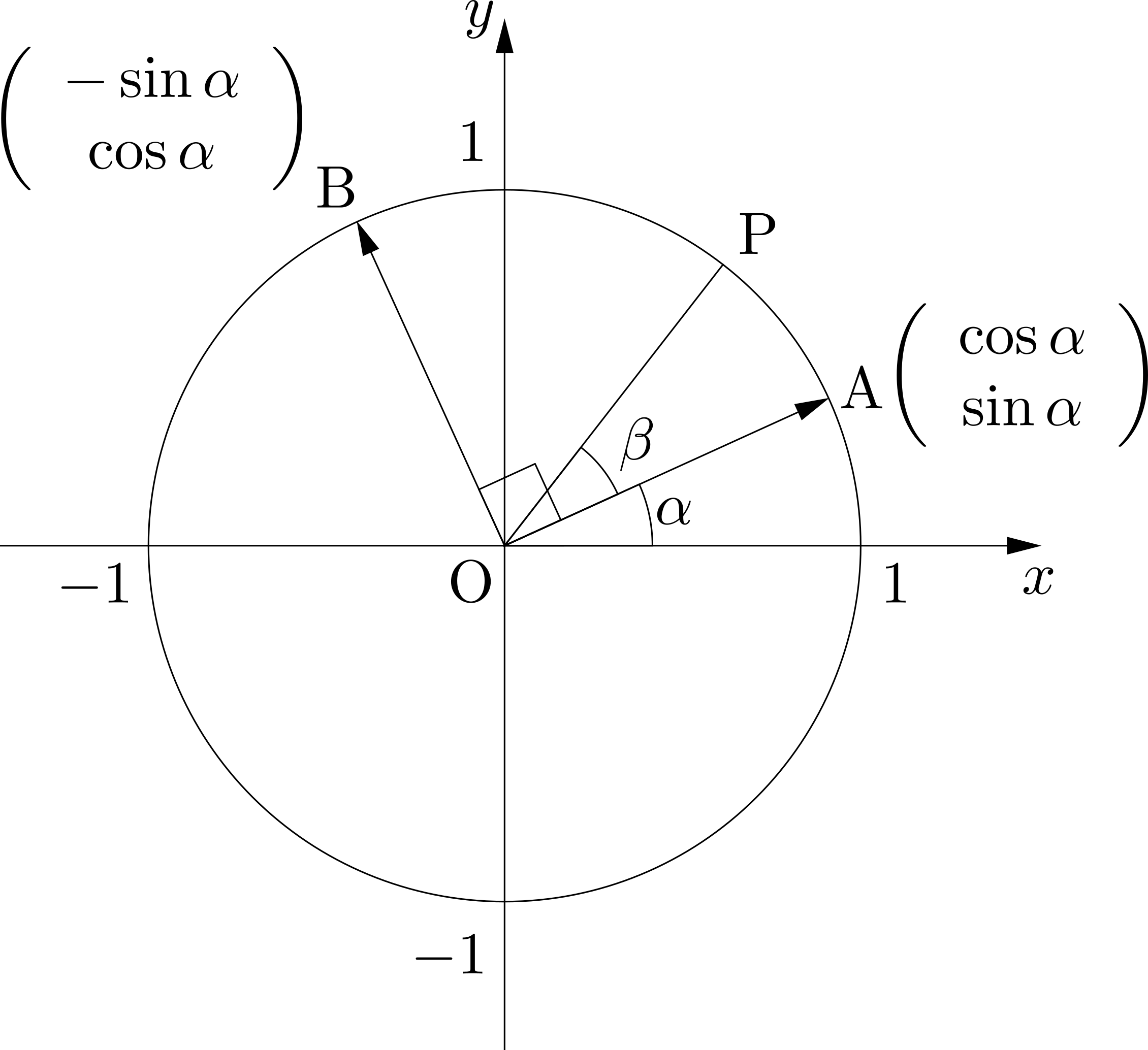
ここに，基本ベクトル\(\overrightarrow{e_1}=\left(\begin{array}{c} 1 \\ 0 \\ \end{array} \right),\overrightarrow{e_2}=\left(\begin{array}{c} 0 \\ 1 \\ \end{array} \right)\)をそれぞれ原点を中心に\(\alpha\)だけ回転させたベクトル\(\overrightarrow{\mathrm{OA}},\overrightarrow{\mathrm{OB}}\)を考え，図示します．\(\mathrm{A}(\cos\alpha,~\sin\alpha),~\mathrm{B}(\cos\left(\frac{\pi}{2}+\alpha\right),~\sin\left(\frac{\pi}{2}+\alpha\right))\)ですから，それらの成分は\[\overrightarrow{\mathrm{OA}}=\left(\begin{array}{c} \cos\alpha \\ \sin\alpha \\ \end{array} \right),\quad\overrightarrow{\mathrm{OB}}=\left(\begin{array}{c} \cos\left(\frac{\pi}{2}+\alpha\right) \\ \sin\left(\frac{\pi}{2}+\alpha\right) \\ \end{array} \right)=\left(\begin{array}{c} -\sin\alpha \\ \cos\alpha \\ \end{array} \right)\]です．

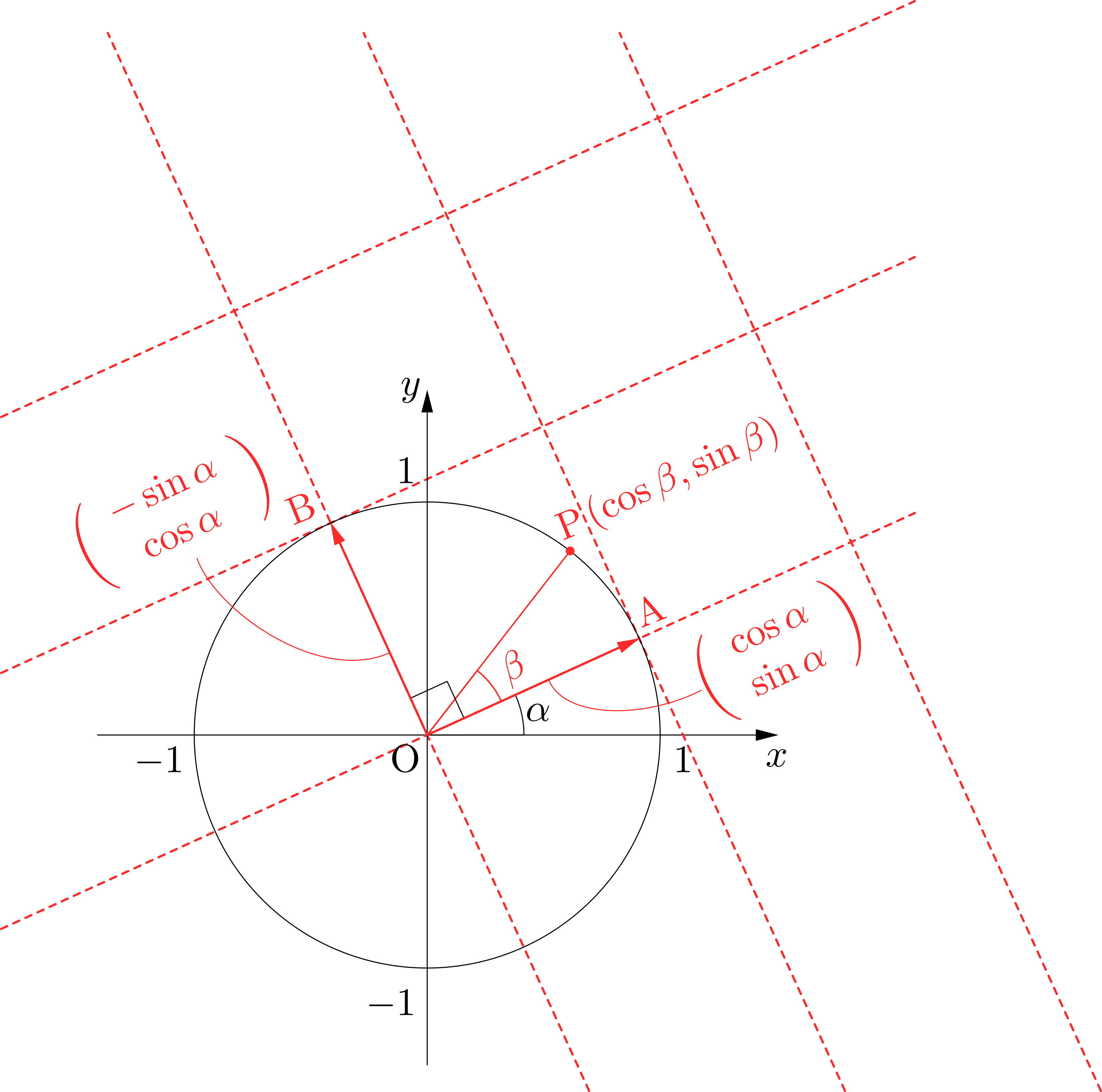
この\(\overrightarrow{\mathrm{OA}}\)，\(\overrightarrow{\mathrm{OB}}\)を基底とする新たな座標系の下でこの点\(\mathrm{P}\)を捉え直します．この新座標系における図の点\(\mathrm{P}\)の座標は，\((\cos\beta,~\sin\beta)\)，すなわち\[
\begin{align*}
\overrightarrow{\mathrm{OP}}
&=\cos\beta\overrightarrow{\mathrm{OA}}+\sin\beta\overrightarrow{\mathrm{OB}}\\
&=\cos\beta\left(\begin{array}{c} \cos\alpha \\ \sin\alpha \\ \end{array} \right)+\sin\beta\left(\begin{array}{c} -\sin\alpha \\ \cos\alpha \\ \end{array} \right)\\
&=\left(\begin{array}{c} \cos\alpha\cos\beta-\sin\alpha\sin\beta \\ \sin\alpha\cos\beta+\cos\alpha\sin\beta \\ \end{array} \right)
\end{align*}\]です．

さらにこれは，
\begin{align*}
\overrightarrow{\mathrm{OP}}&=\left(\begin{array}{c} \cos\alpha\cos\beta-\sin\alpha\sin\beta \\ \sin\alpha\cos\beta+\cos\alpha\sin\beta \\ \end{array} \right)\\
&=(\cos\alpha\cos\beta-\sin\alpha\sin\beta)\left(\begin{array}{c} 1 \\ 0 \\ \end{array} \right)+(\sin\alpha\cos\beta+\cos\alpha\sin\beta)\left(\begin{array}{c} 0 \\ 1 \\ \end{array} \right)\\
&=(\cos\alpha\cos\beta-\sin\alpha\sin\beta)\overrightarrow{e_1}+(\sin\alpha\cos\beta+\cos\alpha\sin\beta)\overrightarrow{e_2}
\end{align*}
これは，点\(\mathrm{P}\)が，\(\overrightarrow{e_1},\overrightarrow{e_2}\)を基底とする（いつもの）座標系においてその座標が\[(\cos\alpha\cos\beta-\sin\alpha\sin\beta,\sin\alpha\cos\beta+\cos\alpha\sin\beta)\tag{1}\]であることを示しています．

他方，\(\overrightarrow{e_1},\overrightarrow{e_2}\)を基底とする座標系における点\(\mathrm{P}\)の座標は\begin{align*}\overrightarrow{\mathrm{OP}}=\left(\begin{array}{c} \cos(\alpha+\beta) \\ \sin(\alpha+\beta) \\ \end{array} \right)=&\cos(\alpha+\beta)\left(\begin{array}{c} 1 \\ 0 \\ \end{array} \right)+\sin(\alpha+\beta)\left(\begin{array}{c} 1 \\ 0 \\ \end{array} \right)\\ =& \cos(\alpha+\beta)\overrightarrow{e_1}+\sin(\alpha+\beta)\overrightarrow{e_2}\end{align*}より\[(\cos(\alpha+\beta),\sin(\alpha+\beta))\tag{2}\]であったから，\((1),(2)\)によって

\begin{eqnarray}
\begin{cases}
\cos(\alpha+\beta) = \cos\alpha\cos\beta-\sin\alpha\sin\beta & \\
\sin(\alpha+\beta) = \sin\alpha\cos\beta+\cos\alpha\sin\beta &
\end{cases}
\end{eqnarray}

が得られます．

証明終

説明しながらの記述なので面倒くさく見えるかもしれませんが，実際やってみると計算らしい計算なしにすぐに作れます。おすすめ。ちなみに\(\alpha-\beta\)の場合については上で得られた式の\(\beta\)を\(-\beta\)に変えれ直ちに手に入ります。（関連：斜交座標）

サイタコスモスコスモスサイタって覚え方を初めて聞いたとき「コスモスサイタサイタコスモスでも通じるじゃん，覚え方として全く意味なくね…？」と思ったし今でもそう思う。

投稿日:

三角不等式

次の不等式を証明せよ．
\[\displaystyle \sum_{i=1}^{n}|x_i+y_i|^p \leq \sum_{i=1}^{n}|x_i||x_i+y_i|^{p-1}+\sum_{i=1}^{n}|y_i||x_i+y_i|^{p-1}\]

高校数学の範囲的には数学Ⅰ（絶対値），数学Ⅱ（不等式の証明，三角不等式），数学B（シグマ計算）あたりかな？

証明
\begin{align*}
|x_i+y_i|^p = &|x_i+y_i||x_i+y_i|^{p-1} \\
\leq &(|x_i|+|y_i|)|x_i+y_i|^{p-1}\\
= &|x_i||x_i+y_i|^{p-1}+|y_i||x_i+y_i|^{p-1}
\end{align*}

この不等式の\(i\)を\(i=1 \cdots n\)とかえて辺々加えて\[\displaystyle \sum_{i=1}^{n}|x_i+y_i|^p \leq \sum_{i=1}^{n}|x_i||x_i+y_i|^{p-1}+\sum_{i=1}^{n}|y_i||x_i+y_i|^{p-1}\]を得る．

証明終

Minkowskiの不等式の証明で使うのでここにnoteしておきます。

高校数学の証明問題としても使えると思いますが三角不等式って高校数学ではそれほど使用頻度が高くないので意外と詰まっちゃう高校生も多い気がします。

投稿日:

不等式の証明と微分法

（数学Ⅲ）

不等式の証明のアプローチのひとつとして微分法の利用があります。

\(p>1,q>1,\frac{1}{p}+\frac{1}{q}=1,a\geq 0,b\geq 0\)とする．このとき，\[ab \leq \frac{a^p}{p}+\frac{b^q}{q}\]を示せ．

証明

まず\(b\geq 0\)を固定して，\[ab \leq \frac{a^p}{p}+\frac{b^q}{q} \Longleftrightarrow~ \frac{1}{p}a^p-ba+\frac{b^q}{q}\geq 0\]と変形し，左辺を\(a\)の関数と見なす．この関数を\(f(a)\)とおく：\[f(a)=\frac{1}{p}a^p-ba+\frac{b^q}{q} \quad (a\geq 0)\]\(f^{\prime}(a)\)を調べると，\[f^{\prime}(a)=a^{p-1}-b\]\(a^{p-1}\)の概形が分からないので，もう一度微分することで\(f^{\prime}(a)\)がどんな概形かを調べる（※）．すると\[f^{\prime\prime}(a)=(p-1)a^{p-2}\geq 0\]したがって\(f^{\prime}(a)\)は増加関数であることが分かる．\(a\geq 0\)であったことに注意して\(a=0\)のときの\(f^{\prime}(a)\)の値を調べると\[f^{\prime}(0)=-b\]

\(b=0\)のときは，\(f^{\prime}(0)=0\)であるから\(f^{\prime}(a)\geq 0\)となる．\(f(0)\)を調べると\(f(0)=\frac{b^q}{q}= 0\)であるから\(f(a)\geq 0\)．（図１）

\(b>0\)のときすなわち\(-b<0\)のときは，\(f^{\prime}(a)=a^{p-1}-b=0 \Longleftrightarrow a=b^{\frac{1}{p-1}}\)で最小値をとる．

そこで\(f\left(b^{\frac{1}{p-1}}\right)\)を調べると
\begin{align*}
f\left(b^{\frac{1}{p-1}}\right)=&\frac{1}{p}\left(b^{\frac{1}{p-1}}\right)^p-b\cdot b^{\frac{1}{p-1}}+\frac{b^q}{q}\\
=&\frac{1}{p}b^{\frac{p}{p-1}}-b^{\frac{p}{p-1}}+\frac{b^q}{q}
\end{align*}
ここで，\(\frac{1}{p}+\frac{1}{q}=1\Leftrightarrow q=\frac{p}{p-1}\)であるから，\[f\left(b^{\frac{1}{p-1}}\right)=\frac{1}{p}b^q-b^q+\frac{1}{q}b^q=\left(\frac{1}{p}+\frac{1}{q}-1\right)b^q=0\]したがって\(f(a)\geq 0\)．（図２）

以上により\[ab \leq \frac{a^p}{p}+\frac{b^q}{q}\]が示された．

証明終

※は概形が図示できず，かつ「差」とみても把握できないタイプなのでもう一回微分して\(f^{\prime\prime}(a)\)を調べました。この記事の「増減表のかきかた」の②”にあたる状況です。

投稿日:

絶対値

生徒に絶対値の定義は？と聞くと十中八九「距離です」と答えます。実際，教科書を見ると

数直線上で，実数\(a\)に対応する点と原点との距離を\(a\)の絶対値といい，記号\(|a|\)で表す

『高等学校 数学Ⅰ』数研出版

 
とあります。\(|3|\)とか\(|-5|\)などを考えるにはこの理解で問題ないでしょう。

しかし，この少し後で学ぶ\(|x|\)や\(|x-4|\)などを含む方程式・不等式が現れると途端に分からなくなる，という生徒がすごく多いのです。確かに「『絶対値は距離』だから\(x-4\)までのキョリ？どういうこと？？」と大混乱してしまうのはまったく無理もないと思います。これは，その生徒ではなく教科書の定義の仕方自体に原因があると思う。「距離」なんてものを持ち出して中途半端に視覚化して理解させようとするから（応用問題において）逆に混乱させてしまう。

というわけで教科書はあまり当てにならないので，手元の微分積分学の本では絶対値をどう定義しているか見てみると，例えば

\(M=\{a,-a\}\)に対し\(\max M=|a|\)とかき，\(a\)の絶対値という．

笠原晧司『微分積分学』サイエンス社

 
とあります。これは換言すれば，次のようになります

絶対値の定義\[|a|:=\begin{cases}a\quad(a\geq 0) \\ -a \quad(a<0)\end{cases}\]

スローガン風に言えば，「‘中身’をムリヤリ正にする記号」，ということです。ここに「数直線」や「距離」などを持ち出す必要はありません。多くの数学書がそうしているように，これを明確に定義とすべきだと思います。このように理解しておけば，上記の\(|x-4|\)の例でいえば

\(|x-4|\)？中身\(x-4\)をムリヤリ正にしたいわけね
→そら中身の\(x-4\)が正か負かで扱い変わるでしょ
→でも\(x-4\)の正負って\(x\)に入る値によって変わるよね
→\(x\geq 4\)なら正なんだからはなから正だわこれ，そのまま外すわ
→\(x<4\)なら負ね，こいつをムリヤリ正にしたいってことは\(-1\)かければいいよね

と自然に頭が動くと思う。

「（困ったら）定義に戻って考える」というのは数学の重要な姿勢のひとつだと思うんですが，そのように定義に立ち戻って考えた人間が混乱するような記述はいかがなものか，と思います（が，教科書通りやらないと注意されたりするんだよなあ…）。

（おわり）

 

 

投稿日:

「すべての」と「ある（存在する）」

数Ⅰの問題です。

\(y=p(x-q)^2+q~(p \neq 0)\)上のすべての点が放物線\(y=x^2-1\)の下側にあるような実数\(q\)が存在するときの実数\(p\)の範囲を求めよ．

まず，「～するときの範囲を求めよ」（「～するための条件を求めよ」）というのは「～するための必要十分条件を求めよ」と問うていると思われます。したがって「\(y=p(x-q)^2+q\)上のすべての点が放物線\(y=x^2-1\)の下側にあるような実数\(q\)が存在する」を同値変形することを考えます。日本語のままでは考えづらいので，この主張を論理記号を用いて表わしてみます。すると\[\exists q \in \mathbb{R} \forall x \in \mathbb{R}[x^2-1>p(x-q)^2+q]\]となります。したがって，

解答

\begin{align*}
&\exists q \in \mathbb{R} \forall x \in \mathbb{R}[x^2-1>p(x-q)^2+q]\\
\Longleftrightarrow~&\exists q \in \mathbb{R} \forall x \in \mathbb{R}[(1-p)x^2+2pqx-pq^2-q-1>0]\\
\Longleftrightarrow~&\exists q \in \mathbb{R} \forall x \in \mathbb{R} \begin{cases}(1-p)x^2+2pqx-pq^2-q-1>0 \\ 1-p>0 \lor 1-p=0 \lor 1-p < 0 \end{cases}\\ \Longleftrightarrow~&\exists q \in \mathbb{R} \forall x \in \mathbb{R}[((1-p)x^2+2pqx-pq^2-q-1>0\land p<1)\\ &\lor ((1-p)x^2+2pqx-pq^2-q-1>0\land p=1) \\
&\lor ((1-p)x^2+2pqx-pq^2-q-1>0\land p>1) ]\tag{1}
\end{align*}
ここで，\[\forall x\in \mathbb{R}[(1-p)x^2+2pqx-pq^2-q-1>0\land p=1]\]と\[\forall x\in \mathbb{R}[(1-p)x^2+2pqx-pq^2-q-1>0\land p>1]\]は偽の命題であるから，\((1)\)は
\[(1)\Longleftrightarrow~\exists q \in \mathbb{R} \forall x \in \mathbb{R}[(1-p)x^2+2pqx-pq^2-q-1>0\land p<1]\]とできる（※）．したがって，
\begin{align*}
(1)\Longleftrightarrow~&\exists q \in \mathbb{R} \forall x \in \mathbb{R}[(1-p)x^2+2pqx-pq^2-q-1>0\land p<1]\\ \Longleftrightarrow~&\exists q \in \mathbb{R} [\forall x \in \mathbb{R}[(1-p)x^2+2pqx-pq^2-q-1>0]\land p<1]\\ \Longleftrightarrow~&\exists q \in \mathbb{R} [p^2q^2-(1-p)(-pq^2-q-1)<0\land p<1]\\ \Longleftrightarrow~&\exists q \in \mathbb{R} [p^2q^2-(1-p)(-pq^2-q-1)<0]\land p<1\\ \Longleftrightarrow~&\begin{cases}\exists q \in \mathbb{R} [pq^2+(1-p)q+1-p<0\land (p >0 \lor p < 0)]\\ p<1 \end{cases}\\ \Longleftrightarrow~&\begin{cases}\exists q \in \mathbb{R} [(pq^2+(1-p)q+1-p<0\land p >0) \lor (pq^2+(1-p)q+1-p<0\land p < 0)]\\ p<1 \end{cases} \\ \Longleftrightarrow~&\begin{cases}\exists q \in \mathbb{R}[pq^2+(1-p)q+1-p<0\land p >0] \lor \exists q \in \mathbb{R}[pq^2+(1-p)q+1-p<0\land p < 0]\\ p<1 \end{cases}\\ \Longleftrightarrow~&\begin{cases}(\exists q \in \mathbb{R}[pq^2+(1-p)q+1-p<0]\land p >0) \lor (\exists q \in \mathbb{R}[pq^2+(1-p)q+1-p<0]\land p < 0)\\ p<1 \end{cases}\\ \Longleftrightarrow~&\begin{cases}((1-p)^2-4p(1-p)>0 \land p>0)\lor p < 0\\ p<1 \end{cases}\\ \Longleftrightarrow~&\begin{cases}((p-1)(5p-1)>0 \land p>0)\lor p < 0\\ p<1 \end{cases}\\ \Longleftrightarrow~&\begin{cases}0 < p < \frac{1}{5}\lor p < 0\\ p<1 \end{cases}\\ \Longleftrightarrow~&0 < p < \frac{1}{5}\lor p < 0 \end{align*} 解答終

一般的な解答においてやっている（であろう）ことの正当性が個人的にいまいち納得できないので，論理式で考えてみました。一般的な解答において感じるその不安感というか気持ち悪さは，上の解答で行っている恒真命題の追加，分配法則，\(\forall\)や\(\exists\)の支配域の変更などがぼかされているためではないかと思います。さらに，この解答においても一つ気になるのが（※）の部分です。一般に，\[\forall x[p(x)\lor q(x)] \Longleftarrow \forall x p(x)\lor \forall x q(x)\]すなわち全称記号は\(\lor\)に関して分配は出来ませんから，そこだけちょっと誤魔化しています。これについては別記事で詳しく考えてみようと思います。

投稿日:

解の公式

解の公式\(a \neq 0\)とする．\[ax^2+bx+c=0\]の解は，\[x=\frac{-b\pm \sqrt{b^2-4ac}}{2a}\]で与えられる．

ちょうど今時期の中学３年生が学ぶ\(2\)次方程式の解の公式です。中学では天下りに与えられ「覚えろ」の一言で済まされることがほとんどだと思いますし，僕自身も授業では証明は割愛しますといって飛ばしがちなので，ここに証明しておきます。見た目は難しそうですが，中学生でも一応既習の知識のみで理解できるはずです。文字の煩雑さに惑わされず，式をよーく睨んで意味を読み取ってみましょう。やっていることはごくごくシンプルです。

証明

\begin{align*}
&ax^2+bx+c=0\\
\Longleftrightarrow&~a\left(x^2+\frac{b}{a}x\right)+c=0\tag{1}\\
\Longleftrightarrow&~a\left(x^2+\frac{b}{a}x+\left(\frac{b}{2a}\right)^2-\left(\frac{b}{2a}\right)^2\right)+c=0\tag{2}\\
\Longleftrightarrow&~a\left(\left(x+\frac{b}{2a}\right)^2-\left(\frac{b}{2a}\right)^2\right)+c=0\tag{3}\\
\Longleftrightarrow&~a\left(x+\frac{b}{2a}\right)^2-a\cdot\frac{b^2}{4a^2}+c=0\tag{4}\\
\Longleftrightarrow&~a\left(x+\frac{b}{2a}\right)^2=\frac{b^2}{4a}-c\\
\Longleftrightarrow&~a\left(x+\frac{b}{2a}\right)^2=\frac{b^2-4ac}{4a}\\
\Longleftrightarrow&~\left(x+\frac{b}{2a}\right)^2=\frac{b^2-4ac}{4a^2}\\
\Longleftrightarrow&~\sqrt{\left(x+\frac{b}{2a}\right)^2}=\sqrt{\frac{b^2-4ac}{4a^2}}\tag{5}\\
\Longleftrightarrow&~\sqrt{\left(x+\frac{b}{2a}\right)^2}=\frac{\sqrt{b^2-4ac}}{\sqrt{(2a)^2}}\\
\Longleftrightarrow&~\left|x+\frac{b}{2a}\right|=\frac{\sqrt{b^2-4ac}}{\left|2a\right|}\tag{6}\\
\Longleftrightarrow&~x+\frac{b}{2a}=\pm\frac{\sqrt{b^2-4ac}}{2a}\tag{7}\\
\Longleftrightarrow&~x=-\frac{b}{2a}\pm\frac{\sqrt{b^2-4ac}}{2a}\\
\Longleftrightarrow&~x=\frac{-b\pm\sqrt{b^2-4ac}}{2a}
\end{align*}

証明終

\((1)\)は２つめの項までを\(a\)でくくりました。
\((2)\)は\(\left(\frac{b}{2a}\right)^2\)をたして，ひきました。プラマイゼロになるので結局\(0\)を加えているに過ぎず，したがって問題ありません。なぜそんなことをするのかというと，
\((3)\)で因数分解の公式\(x^2+2Ax+A^2=(x+A)^2\)が使えるようにするためです。
\((4)\)は分配法則により\(a\)を分配し，
\((5)\)は辺々\(\sqrt{　}\)をとりました。
\((6)\)は\(\sqrt{A^2}\)の定義を思い出しましょう。\(\sqrt{A^2}\)とは，「\(2\)乗して\(A^2\)となる正の数」でした。それは何ですか？「\(A\)」と答えた人，甘い。\(A\)が負の数である可能性は？例えば，\(A=-1\)なら？\(\sqrt{(-1)^2}=-1\)ってこと？「正の数」と定義したのに，負の数？？おかしい。つまり，\(A\)がたとえ負の数であっても，正の数として表したいわけです。いわば，\(A\)の中身が正であろうが負であろうが，正の数として表したい。そんなときのための記号が，絶対値でしたね（絶対値の定義を「距離」として覚えてる人がいますが，今すぐ止めましょう）。なので\(\sqrt{A}=|A|\)
\((7)\)絶対値の“中身”の起こり得る組合せに着目して
\begin{align*}
&\text{\(x\)+\(\frac{b}{2a}\)が正，\(2a\)が正}\\
&\text{\(x\)+\(\frac{b}{2a}\)が正，\(2a\)が負}\\
&\text{\(x\)+\(\frac{b}{2a}\)が負，\(2a\)が正}\\
&\text{\(x\)+\(\frac{b}{2a}\)が負，\(2a\)が負}\\
\end{align*}の４通りの組み合わせがあることに注意すれば
\begin{align*}
(6)\Longleftrightarrow &+\left(x+\frac{b}{2a}\right)=\frac{\sqrt{b^2-4ac}}{+(2a)} \lor +\left(x+\frac{b}{2a}\right)=\frac{\sqrt{b^2-4ac}}{-(2a)}\\
&\lor-\left(x+\frac{b}{2a}\right)=\frac{\sqrt{b^2-4ac}}{+(2a)} \lor -\left(x+\frac{b}{2a}\right)=\frac{\sqrt{b^2-4ac}}{-(2a)}\\
\Longleftrightarrow &\left(x+\frac{b}{2a}\right)=+\frac{\sqrt{b^2-4ac}}{2a} \lor \left(x+\frac{b}{2a}\right)=-\frac{\sqrt{b^2-4ac}}{2a}\\
&\lor \left(x+\frac{b}{2a}\right)=-\frac{\sqrt{b^2-4ac}}{2a} \lor \left(x+\frac{b}{2a}\right)=+\frac{\sqrt{b^2-4ac}}{2a}\\
\Longleftrightarrow &x+\frac{b}{2a}=+\frac{\sqrt{b^2-4ac}}{2a} \lor x+\frac{b}{2a}=-\frac{\sqrt{b^2-4ac}}{2a}\\
\Longleftrightarrow &x+\frac{b}{2a}=\pm\frac{\sqrt{b^2-4ac}}{2a}
\end{align*}となります。

投稿日:

★P270

\((a_n)_{n\in \mathbb{N}},(b_n)_{n\in \mathbb{N}}\)を\(\mathbb{R}\)の点列とする．このとき\[\lim_{n\rightarrow \infty} a_n =a,~\lim_{n\rightarrow \infty} b_n =b,~a_n\leq b_n \Longrightarrow a \leq b\]

証明の途中で出てきました。直観的にはマジで明らかだけどちょっと気になったので調べてみます。高校数学ではこれをアタリマエとして使っていると思います。\(a_n\leq b_n\)はもちろん\(\forall n \in \mathbb{N} [a_n\leq b_n]\)の略記です。

証明

\[\lim_{n\rightarrow \infty} a_n =a,\lim_{n\rightarrow \infty} b_n =b,a_n\leq b_n \land a > b\]と仮定する．\(\forall \epsilon >0 \exists n_1\in \mathbb{N} [n>n_1 \Rightarrow d(a_n,a)<\epsilon]\)であるから\(\epsilon\)として例えば\(\frac{a-b}{3}>0\)をとると，
\begin{align*}
d(a_n,a)<\frac{a-b}{3}\Longleftrightarrow~&|a_n-a| < \frac{a-b}{3}\\ \Longleftrightarrow~&-\frac{a-b}{3}< a_n-a < \frac{a-b}{3}\\ \Longleftrightarrow~&a-\frac{a-b}{3}< a_n < a+\frac{a-b}{3}\\ \end{align*}他方，\(\forall \epsilon >0 \exists n_2\in \mathbb{N} [n>n_2 \Rightarrow d(b_n,b)<\epsilon]\)であるから上と同様に\(\epsilon=\frac{a-b}{3}>0\)として\[d(b_n,b)<\frac{a-b}{3}\Longleftrightarrow~b-\frac{a-b}{3}< b_n < b+\frac{a-b}{3}\]ここで，\[a-\frac{a-b}{3}-\left(b+\frac{a-b}{3}\right)=\frac{a-b}{3}>0\]これは\(a_n \leq b_n\)に反する．

証明終

これで安心(^^)！（死んだ目）

投稿日:

★P263（問題4の一部）

\[\forall \epsilon >0 \exists \delta >0[d^{\prime\prime}(x,y) \Longrightarrow d(x,y)<\epsilon]\]を示せ．ただし，\(d^{\prime\prime}(x,y):=\min\{1,d(x,y)\}\)

証明

与えられた\(\epsilon\)が\(\epsilon < 1\)であれば\(\delta = \epsilon\)と定め，\(\epsilon \geq 1\)であれば\(\delta = \delta^{\prime} < 1 (\leq \epsilon)\)と定めればよい．以下，それを確かめる．

\(\epsilon < 1\)のとき：
\(d^{\prime\prime}(x,y):=\min\{1,d(x,y)\}<\epsilon \)．\(1 \leq d(x,y)\)とすれば\(\min\{1,d(x,y)\}=1<\epsilon\)となり矛盾．したがって\(1>d(x,y)\)である．このとき，\(\min\{1,d(x,y)\}=d(x,y)<\epsilon\)

\(\epsilon \geq 1\)のとき：
\(d^{\prime\prime}(x,y):=\min\{1,d(x,y)\}<\delta^{\prime}(<1)\)．\(1 \leq d(x,y)\)とすれば\(\min\{1,d(x,y)\}=1<\delta^{\prime}<1\)となり矛盾．したがって\(1>d(x,y)\)である．このとき\(\min\{1,d(x,y)\}=d(x,y)<\delta^{\prime}<1\leq \epsilon\)より\(d(x,y)<\epsilon\)

証明終

多分簡単な問題だと思うんですけど任意に与えられた正数\(\epsilon\)をそのままで\(\delta\)探しして結構時間がかかってしまった…

これ記法や表現を適当に変えれば高校生向けの論理の問題に出来る気がします。

© 2024 佐々木数学塾, All rights reserved.