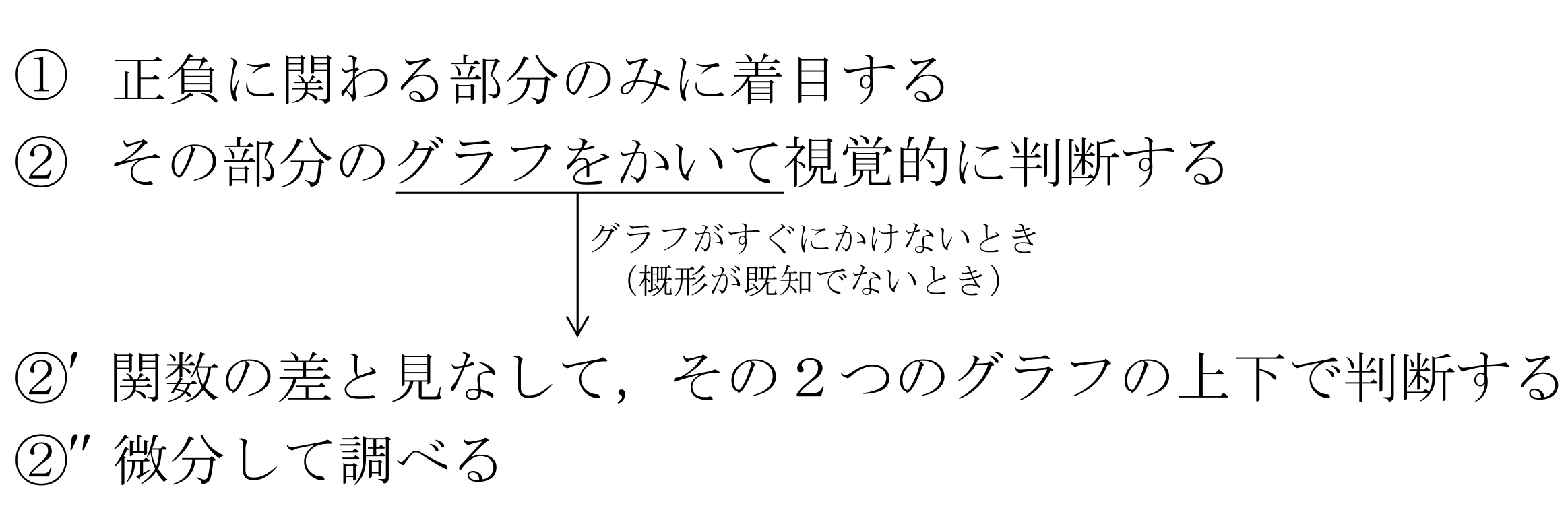
チャート式なんかによくみる解法
\(2\)次方程式\(f(x)=0\)が異なる\(2\)つの負の解をもつ\(~\Longleftrightarrow D>0,\alpha+\beta <0,\alpha\beta < 0\)
\(2\)次方程式\(f(x)=0\)が異符号の解をもつ\(~\Longleftrightarrow \alpha\beta < 0 \)
これを見てふと思う。最後のだけなんで\(D>0\)がないの?と。補足をよく見ると「このとき,\(D>0\)は成り立っている」と小さく書いてある。ここ,ちょっと疑問をもちつつも「まあそういうもんなんだろ~」程度のゆるい理解で済ませているひとも少なくないと思います。でも,ここをちゃんと確認しないまま結果だけ使うというのは,理由を納得しないまま覚えるということで,数学としてはその姿勢はちょっと不安です。
証明してみます。以下,\(\alpha,\beta\)を\(2\)次方程式\(f(x)=0\)の解とします。
証明
\(2\)次方程式\(f(x)=0\)が異符号の解をもつとする.
\begin{align*}
&~\text{\(2\)次不等式\(f(x)=0\)が異符号の解をもつ}\\
\Longleftrightarrow &~D>0 \land ((\alpha > 0 \land \beta < 0) \lor (\alpha < 0 \land \beta > 0))\\
\Longleftrightarrow &~D>0 \land \alpha\beta < 0\\
\Longrightarrow &~\alpha\beta < 0 \quad\text{※ 必要条件}
\end{align*}よって,\[\text{\(2\)次不等式\(f(x)=0\)が異符号の解をもつ}\Longrightarrow ~\alpha\beta < 0\]が成り立つ.逆に,\(\alpha\beta < 0\)とする.
\begin{align*}
\alpha\beta=\frac{c}{a}<0 \Longleftrightarrow~& ac<0\\ \Longleftrightarrow~& -4ac > 0\\
\Longrightarrow~& b^2-4ac > 0 \quad\text{※ 必要条件}\\
\Longleftrightarrow~& D > 0
\end{align*}ゆえに,
\begin{align*}
\alpha\beta < 0 \Longrightarrow~&D>0 \land \alpha\beta < 0\\
\Longleftrightarrow~&\text{\(2\)次不等式\(f(x)=0\)が異符号の解をもつ}
\end{align*}以上により,\[\text{\(2\)次不等式\(f(x)=0\)が異符号の解をもつ}\Longleftrightarrow~\alpha\beta < 0\]が示された.
証明終
判別式と解と係数の関係どーのこーのがこの分野のテーマだと思うんですが,そんなことより補足として小さく書かれたこっちの議論の方が大事だし面白いと個人的に思います^^;
そもそも,教科書や教科書準拠問題集はそもそもこの辺の論理にはあまり深入りしない傾向がある気がします。卑近な例ですが例えば「判別式は\(D\)じゃなくて\(\frac{D}{4}\)を使うと計算が楽だよ!」とか。これだって,「判別式はあくまで\(D\)であって,\(\frac{D}{4}\)だなんて勝手に\(\frac{1}{4}\)しちゃだめだろ」と思いませんでしたか…?僕は思ったなあ。実際楽なので正当性も確かめずに使ってましたが。まあともかくこれだって,なんのことはない,\begin{align*}D > 0 \Longleftrightarrow \frac{D}{4}>0\\
D = 0 \Longleftrightarrow \frac{D}{4}=0\\
D < 0 \Longleftrightarrow \frac{D}{4} <0\\
\end{align*}ということに過ぎず,したがって例えば\(\frac{D}{4}>0\)を変形して得られる結論は,\(D>0\)と同値であるわけです。だから\(\frac{D}{4}>0\)で考えてよい,という。
もっとも,細かいことは気にせずとりあえず使えるように(=問題が解けて,点数がもらえるように)なることを目指し,その後改めて,細部を振り返り精査していく…という勉強法は難しい内容を学びとるためのひとつの有効な姿勢であり,決して否定はできません。あまり細かいことを言うと敷居が高くなったり(※誤用の方),あるいは深入りしすぎて手段と目的が逆転してしまったりといいことばかりではありませんしね。どう導入するのか,というのは難しいところです。




 \((1)\)について:
\((1)\)について:
 \((3)\)について:
\((3)\)について: