この記事で絶対値を含む方程式,不等式に関する公式を証明しました。この公式は,右辺が正の定数であることしか仮定しておらず,したがって右辺が負の数や\(0\)の場合においても成り立つことは保証していません。なので,右辺に文字を含む場合は一般的には「(定義に従って)場合分けして解く」と学ぶことが多いと思います。しかし実は,右辺に文字を含む含まないに関わらず(つまり正か\(0\)か負かに関わらず),次が成り立ちます。
(1)\quad~&|\mathrm{A}|=B \Longleftrightarrow \mathrm{A}=\pm B \land \mathrm{B}>0 \\
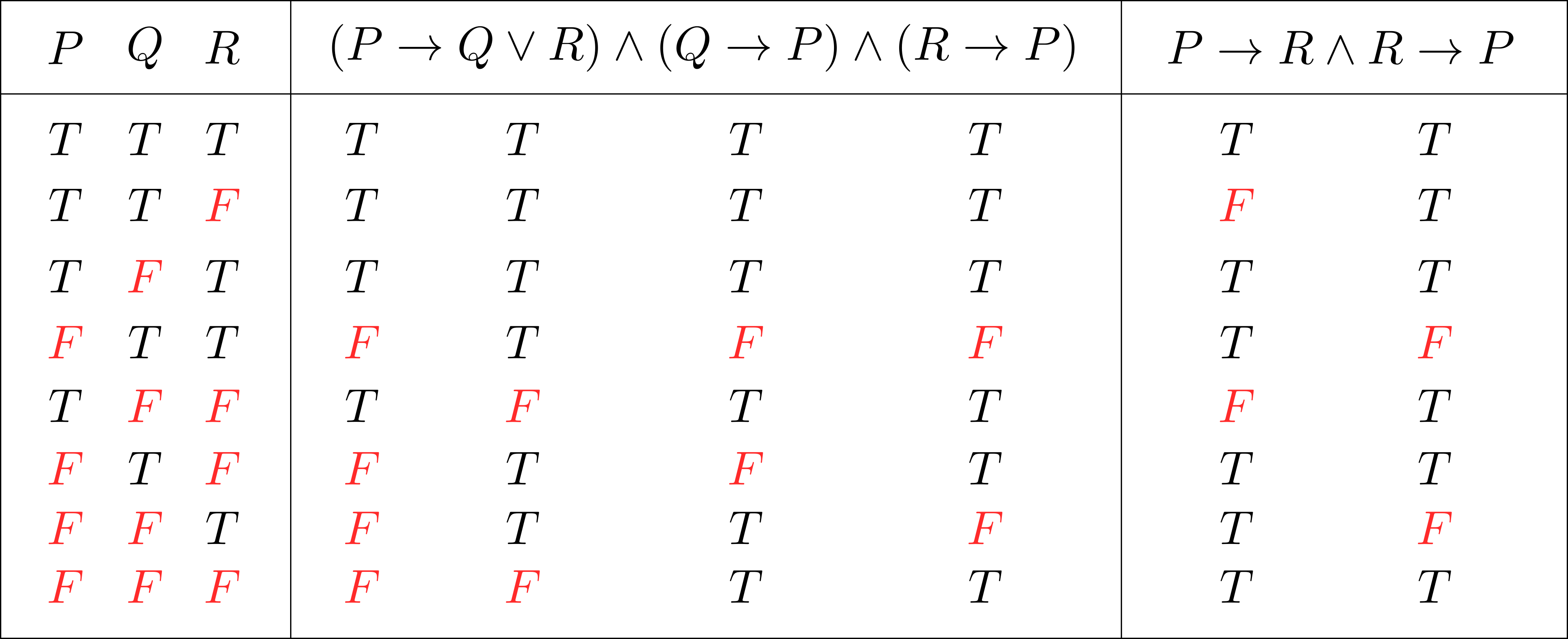
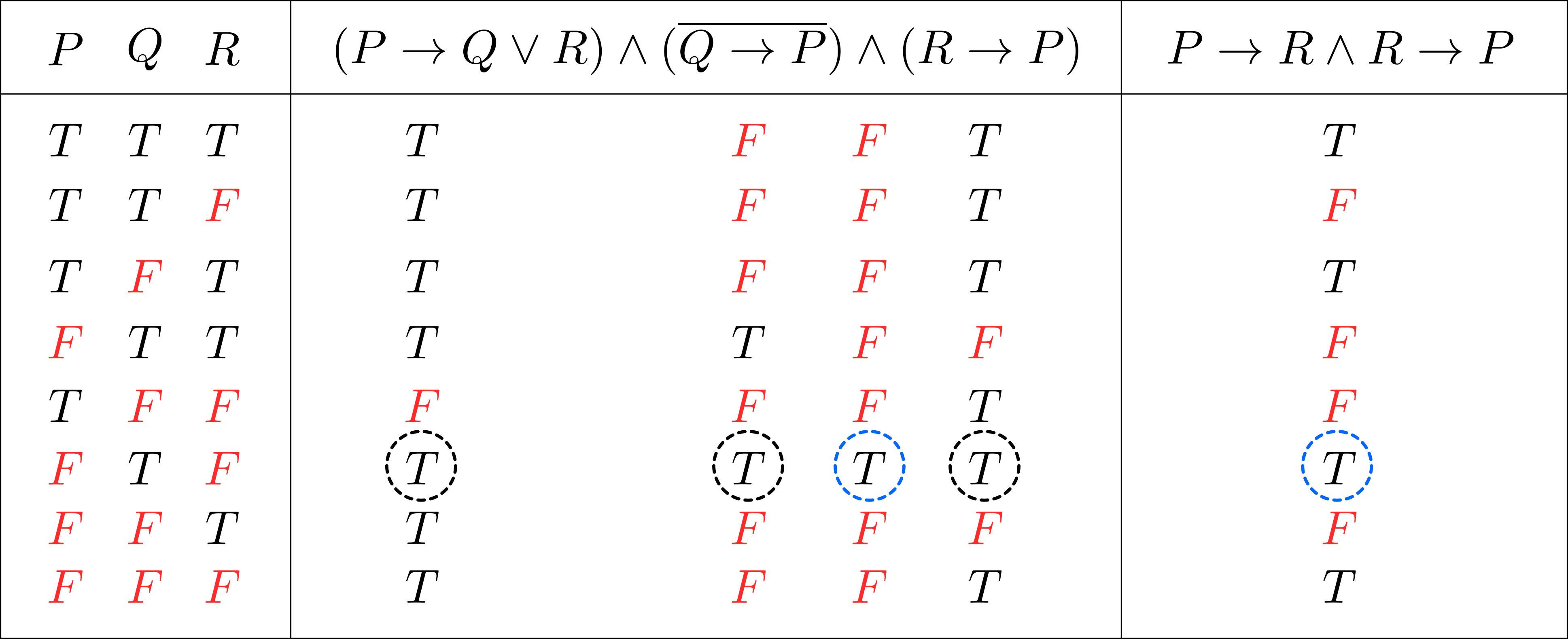
(2)\quad~&|\mathrm{A}| < \mathrm{B} \Longleftrightarrow -B < A < B \\ (3)\quad~&|\mathrm{A}|>\mathrm{B} \Longleftrightarrow \mathrm{A}<-B \lor \mathrm{B} < A \\
\end{align*}
\((1)\)は明らかなので,\((2)\)と\((3)\)を証明します。
\((2)\)の証明
\begin{align*}
&|\mathrm{A}| < \mathrm{B} \\
\Longleftrightarrow~&|\mathrm{A}| < \mathrm{B}\land(\mathrm{B}>0 \lor \mathrm{B}=0 \lor \mathrm{B}<0)\\
\Longleftrightarrow~&(|\mathrm{A}| < \mathrm{B}\land \mathrm{B}>0)\lor(|\mathrm{A}| < \mathrm{B}\land \mathrm{B}=0) \lor (|\mathrm{A}| < \mathrm{B} \land \mathrm{B}<0))\\
\Longleftrightarrow~&(|\mathrm{A}| < \mathrm{B}\land \mathrm{B}>0)\lor(|\mathrm{A}| < 0\land \mathrm{B}=0) \lor (|\mathrm{A}| < \mathrm{B} \land \mathrm{B}<0))\\
\Longleftrightarrow~&(-\mathrm{B} < \mathrm{A} < \mathrm{B}\land \mathrm{B}>0)\lor (\bot \land \mathrm{B}=0) \lor \bot\\
\Longleftrightarrow~&(-\mathrm{B} < \mathrm{A} < \mathrm{B}\land \mathrm{B}>0)\lor \bot \lor \bot\\
\Longleftrightarrow~&-\mathrm{B} < \mathrm{A} < \mathrm{B}\land \mathrm{B}>0\\
\Longleftrightarrow~&-\mathrm{B}<\mathrm{A}< \mathrm{B}
\end{align*}
\(|\mathrm{A}|=\max\{-\mathrm{A},\mathrm{A}\}\)であることに注意すると,下記のように簡潔に記述できます:
\begin{align*}
&|\mathrm{A}| < \mathrm{B} \\
\Longleftrightarrow~&\max\{\mathrm{A},-\mathrm{A}\} < \mathrm{B}\\
\Longleftrightarrow~&\mathrm{A}< \mathrm{B}\land-\mathrm{A}< \mathrm{B}\\
\Longleftrightarrow~&-\mathrm{B}<\mathrm{A}< \mathrm{B}
\end{align*}
\((3)\)の証明
&|\mathrm{A}| > \mathrm{B} \\
\Longleftrightarrow~&|\mathrm{A}| > \mathrm{B}\land(\mathrm{B}>0 \lor \mathrm{B}=0 \lor \mathrm{B}<0)\\ \Longleftrightarrow~&(|\mathrm{A}| > \mathrm{B}\land \mathrm{B}>0 )\lor(|\mathrm{A}| > \mathrm{B}\land \mathrm{B}=0) \lor (|\mathrm{A}| > \mathrm{B} \land \mathrm{B}<0))\\
\Longleftrightarrow~&((\mathrm{A} < -\mathrm{B} \lor \mathrm{B} < \mathrm{A}) \land \mathrm{B} >0) \lor (|\mathrm{A}|>0 \land B=0) \lor ( \mathrm{A}\in \mathbb{R} \land \mathrm{B}<0)\\
\Longleftrightarrow~&((\mathrm{A} < -\mathrm{B} \lor \mathrm{B} < \mathrm{A}) \land \mathrm{B} >0) \lor (\mathrm{A}\neq 0 \land B=0) \lor ((\mathrm{B} < \mathrm{A} \lor \mathrm{A} < -\mathrm{B}) \land \mathrm{B}<0)\\
\Longleftrightarrow~&((\mathrm{A} < -\mathrm{B} \lor \mathrm{B} < \mathrm{A}) \land \mathrm{B} >0) \lor ((\mathrm{A}<0\lor 0<\mathrm{A})\land B=0) \lor ((\mathrm{A} < -\mathrm{B} \lor \mathrm{B} < \mathrm{A}) \land \mathrm{B}<0)\\
\Longleftrightarrow~&((\mathrm{A} < -\mathrm{B} \lor \mathrm{B} < \mathrm{A}) \land \mathrm{B} >0) \lor ((\mathrm{A}<-B\lor B<\mathrm{A}) \land B=0) \lor ((\mathrm{A} < -\mathrm{B} \lor \mathrm{B} < \mathrm{A}) \land \mathrm{B}<0)\\
\Longleftrightarrow~& (\mathrm{A} < -\mathrm{B} \lor \mathrm{B} < \mathrm{A}) \land(\mathrm{B}>0 \lor \mathrm{B}=0 \lor \mathrm{B}<0)\\
\Longleftrightarrow~& (\mathrm{A} < -\mathrm{B} \lor \mathrm{B} < \mathrm{A}) \land \top\\
\Longleftrightarrow~& \mathrm{A} < -\mathrm{B} \lor \mathrm{B} < \mathrm{A}\\ \end{align*}
または上と同様に, \begin{align*} &|\mathrm{A}| > \mathrm{B} \\
\Longleftrightarrow~&\max\{\mathrm{A},-\mathrm{A}\} > \mathrm{B}\\
\Longleftrightarrow~&\mathrm{A} > \mathrm{B}\lor-\mathrm{A}> \mathrm{B}\\
\Longleftrightarrow~&\mathrm{A}>\mathrm{B} \lor \mathrm{A} < -\mathrm{B}\\
\Longleftrightarrow~&\mathrm{A} < -\mathrm{B} \lor \mathrm{B} < \mathrm{A}
\end{align*}
証明終
これでいちおう,機械的に解けます。