\((1)\)異なる\(4\)つの共有点をもつとき,定数\(k\)の値の範囲を求めよ.
\((2)\)放物線と円が接するとき,定数\(k\)の値を求めよ.
円と放物線が共有点をもつときの\(k\)の範囲を\(\mathcal{D}\)とおく.
\begin{align*}
&k\in\mathcal{D}\\
\Longleftrightarrow~ &\exists x \exists y \begin{cases}x^2+y^2=4 \\ y=x^2+k\end{cases}\\
\Longleftrightarrow~ &\exists x \exists y \begin{cases}x^2+y^2=4 \\ y=(4-y^2)+k\end{cases}\\
\Longleftrightarrow~ &\exists x \exists y \begin{cases}x^2=4-y^2 \\ y^2+y-4-k=0\end{cases}\\
\Longleftrightarrow~ &\exists y\left[\exists x [x^2=4-y^2] \land y^2+y-4-k=0 \right]\\
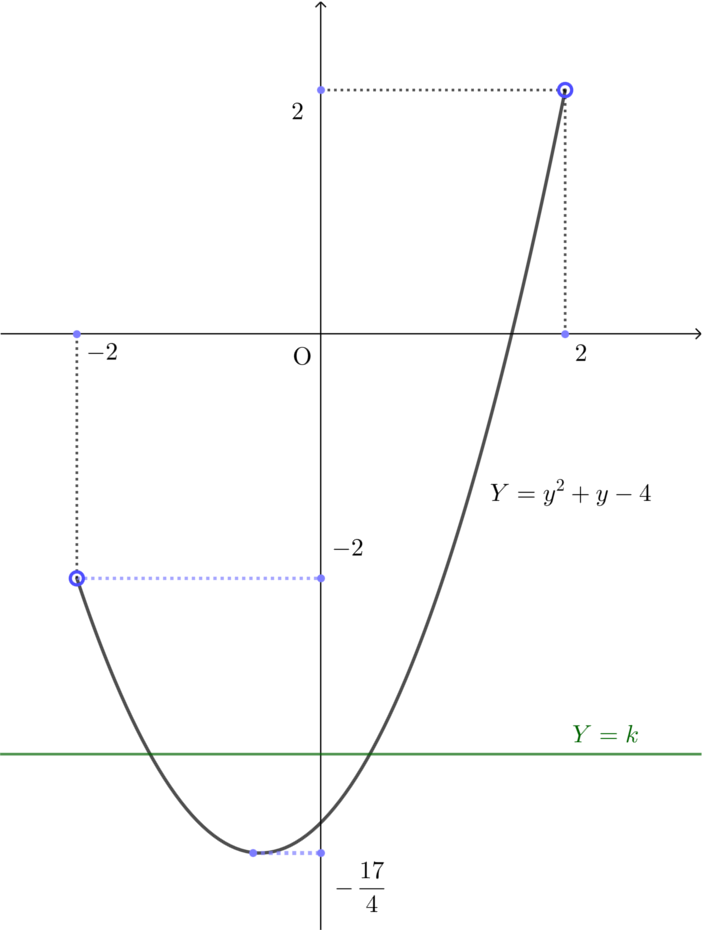
\Longleftrightarrow~ &\exists y\left[-2 \leq y \leq 2 \land y^2+y-4=k \right]\\
\Longleftrightarrow~ &\exists y\left[-2 \leq y \leq 2 \land \left(y+\frac{1}{2}\right)^2-\frac{17}{4}=k \right]\\
\Longleftrightarrow~ &-\frac{17}{4} \leq k \leq 2 \tag{\(\ast\)}
\end{align*}
\((2)~\)上の結果と下図から,接するとき,\(k=\pm 2\)または\(k=-\frac{17}{4}\).
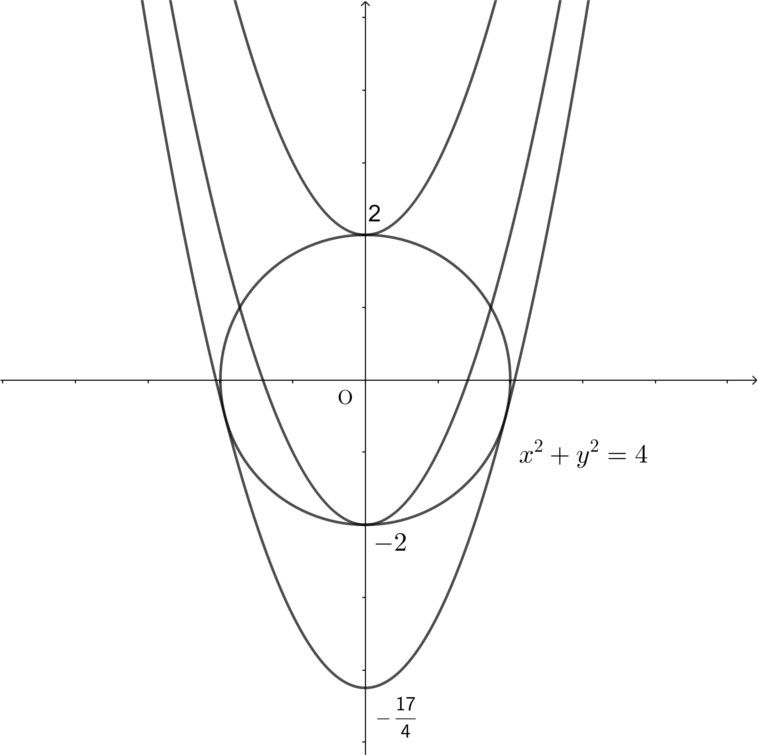
\((1)~\)\((2)\)の考察と上図から,異なる\(4\)つの共有点をもつとき,\(-\frac{17}{4} < k < -2\).
\((\ast)\)の考察は下図による(文字定数は分離せよ,の方針).