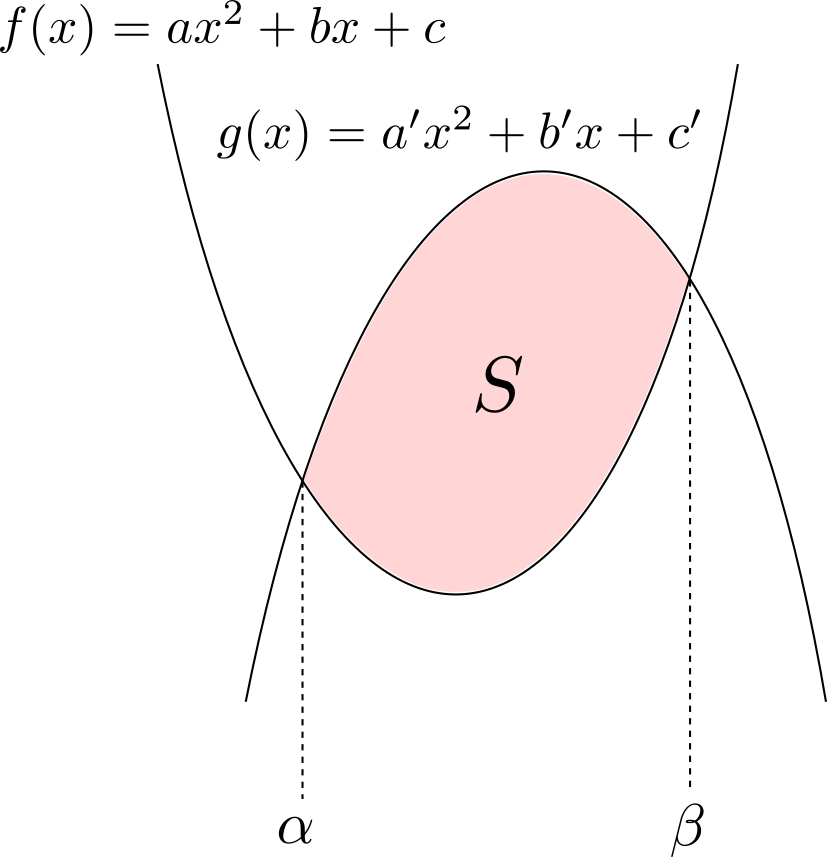
上の\(2\)つの放物線と直線で囲まれる部分の面積\(S\)は,\[S = \frac{|a’-a|(\beta-\alpha)^3}{6}\]で表される.
証明
被積分関数\(g(x)-f(x)\)がどんな関数になるかを考える.これは,
-
-
- \(2\)次式で,
- 次数が一番大きい項の係数は\(a’-a\)で,
- \(x=\alpha,x=\beta\)で交わる,すなわち\(g(x)-f(x)=0\)を解いて得られる\(2\)つの解が\(\alpha,\beta\)である
-
ことに着目すると,\[g(x)-f(x) = (a’-a)(x-\alpha)(x-\beta)\]とかける.したがって求める部分の面積は
\begin{align*}
&\displaystyle \int_{\alpha}^{\beta} (a’-a)(x-\alpha)(x-\beta) dx \\
=~&\displaystyle (a-a’)\int_{\alpha}^{\beta} -(x-\alpha)(x-\beta) dx\\
=~&\frac{(a-a’)(\beta-\alpha)^3}{6}\tag{1}\\
=~&\frac{|a’-a|(\beta-\alpha)^3}{6}
\end{align*}証明終
\(|a’-a|\)はもちろん\(|a-a’|\)でもいいです.要は上下関係なく機械的に‘係数の差’の絶対値をとればいい,ということです.\((1)\)はここの公式によります.

