高校教科書では,定積分を次のように定義しています.
\(f(x)\)の原始関数の1つを\(F(x)\)とする.
\[\int^b_af(x)dx:=F(b)-F(a)\]
そして,数学Ⅱまたは数学Ⅲで積分を既習の人はこの定積分を計算することによって「面積が求まる」ということも知っていると思います.
しかし,ここでひとつ疑問.なぜ定積分で面積が求まるのでしょうか?定積分の定義は上に示したようにあくまで「原始関数の差を『定積分』と呼ぶことにしましょう」と言っているに過ぎず,「面積」云々には一切触れていません.つまり(定積分の「定義」から)「面積が求まる」ということが「定理」として得られるはずですが,その理由はどこにあるのでしょうか?その辺を理解しないままにただただ計算している人も多いのではないでしょうか.
調べてみましょう.
今,\(y=f(x),~x\leq k,~y=0\)で示される部分の面積を\(S(k)\)と表すことにします.

すると,\(y=f(x),~x=x_1,~x=x_2,~y=0\)で囲まれる部分の面積は,\[S(x_2)-S(x_1)\]で表されることになります.
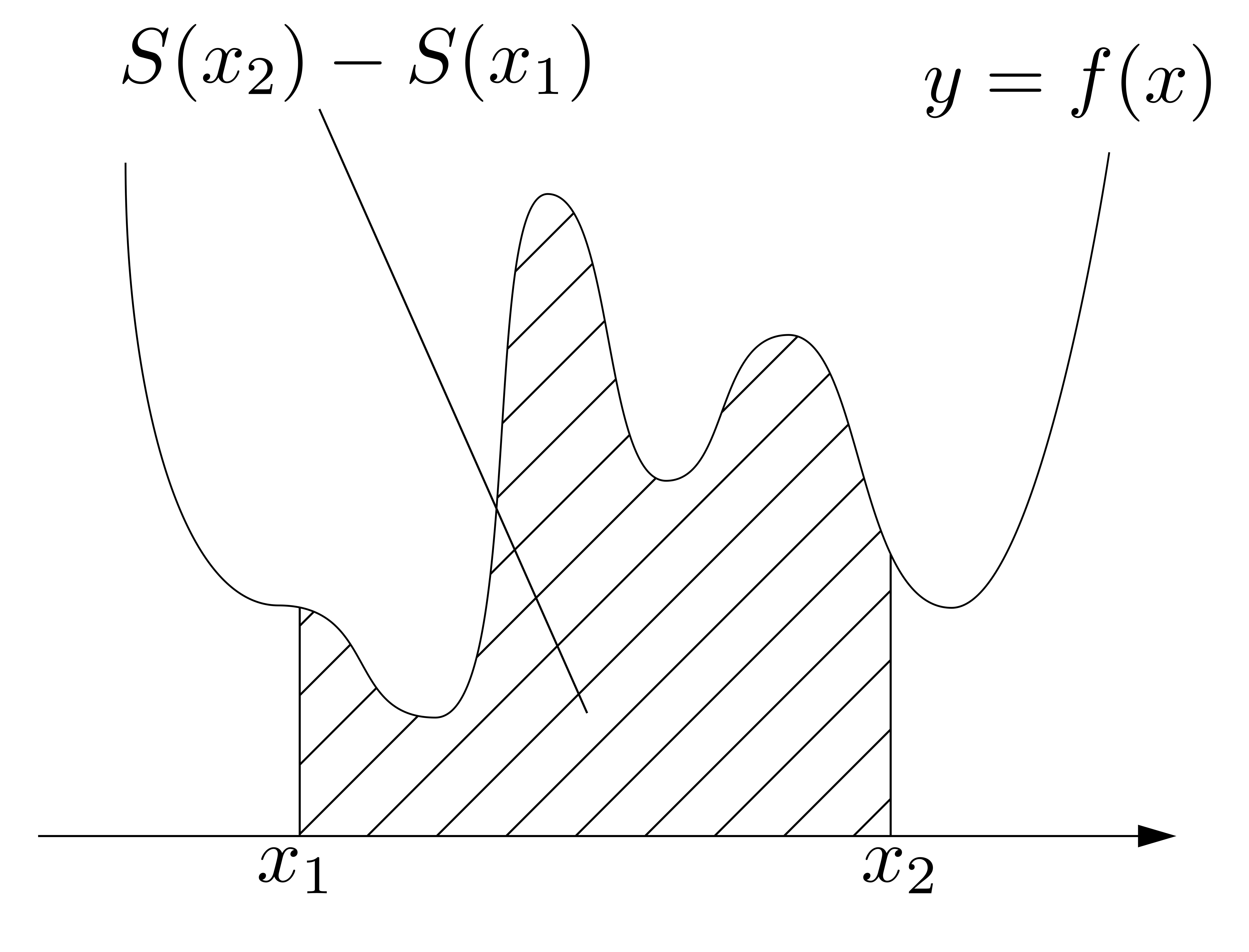
この斜線部分の面積を評価することを考えます.斜線部分の面積\(S(x_2)-S(x_1)\)は,区間\([x_1,~x_2]\)の幅\(x_2-x_1\)を「ヨコ」,区間\([x_1,~x_2]\)で一番大きい\(y\)の値\(f(x_{max})\)を「タテ」としたときの長方形の面積\((x_2-x_1)f(x_{max})\)より小さく,区間\([x_1,~x_2]\)の幅\(x_2-x_1\)を「ヨコ」,区間\([x_1,~x_2]\)で一番小さい\(y\)の値\(f(x_{min})\)を「タテ」としたときの長方形の面積\((x_2-x_1)f(x_{min})\)よりも大きいと言えます(下図参照.一番大きい,または小さい\(y\)の値を取るときの\(x\)をそれぞれ\(x_{max},~x_{min}\)とおきました).
したがって,以下の不等式が成り立ちます.
\[(x_2-x_1)f(x_{min})\leq S(x_2)-S(x_1)\leq (x_2-x_1)f(x_{max})\]
さらに,辺々を\(x_2-x_1\)で割ることで,
\[f(x_{min})\leq \frac{S(x_2)-S(x_1)}{x_2-x_1}\leq f(x_{max})\]
が得られます.
ここで,\(x_2\)を\(x_1\)に近づけてみます.すなわち,
\[\lim_{x_2\rightarrow x_1}f(x_{min})\leq \lim_{x_2\rightarrow x_1}\frac{S(x_2)-S(x_1)}{x_2-x_1}\leq \lim_{x_2\rightarrow x_1}f(x_{max})\]
まず中辺ですが,これは導関数の定義から\[S'(x_1)\]と書けます.
次に左辺と右辺について.\(x_2\)を\(x_1\)に近づけるというのは,区間\([x_1,x_2]\)の幅を縮めるということですから,図から\(f(x_{max}),~f(x_{min})\)はどちらも\(f(x_1)\)に近づくことが分かります(下図参照).

すなわち,
\[\lim_{x_2\rightarrow x_1}f(x_{max})=\lim_{x_2\rightarrow x_1}f(x_{max})=f(x_1)\]
したがって,はさみうちの原理から
\[S'(x_1)=f(x_1)\]
が得られますが,この式は
\[S(x_1)=\text{\(f(x_1)\)の原始関数}\]
であることを示しています.添え字がちょっとうるさいので\(x_1\)を\(x\)に置き換えておきます.
\[S(x)=\text{\(f(x)\)の原始関数}\]
準備は整いました.定積分の定義\(\displaystyle \int^b_a f(x)dx=F(b)-F(a)\)を変形してみます.
\[
\begin{align}
\int^b_a f(x)dx=&F(b)-F(a)\\
=&\text{\(f(x)\)の原始関数}|_{x=b}-\text{\(f(x)\)の原始関数}|_{x=a}\tag{1}\\
=&S(x)|_{x=b}-S(x)|_{x=a}\tag{2}\\
=&S(b)-S(a)
\end{align}
\]
\((1)\)は定義の仮定:「\(F(x)=\text{\(f(x)\)の原始関数}\)」から,
\((2)\)は先に導いた式:「\(S(x)=\text{\(f(x)\)の原始関数}\)」によるものです.
結局,
\[\int^b_a f(x)dx=S(b)-S(a)\]
が得られますが,\(S(b)-S(a)\)は\(y=f(x),~x=a,~x=b,~y=0\)で囲まれた面積を表しますから,定積分すなわち原始関数の差は確かに面積を表すことが確認でしました.
以上により定積分で面積が求められることが一応納得はできました.しかしながら,この「納得」は上でみたように複雑で,お世辞にも「直観的」とは言えません.一般に求積問題は図形が絡むので視覚情報から解法に繋げていくことが多いのですが,その視覚情報を数式に落とし込むにはある種の「直観的」な理解が必要になってきます.教科書の定義のままでは直観的な理解が伴わないゆえに求積問題等ではうまく発想・立式ができず,ほとんど使い物になりません.数学が得意な人,これから得意にしたい人,あるいは将来的に数学を使う学部学科に進みたい人は違う角度で定積分というものを捉える(理解する)べきです.
次回,「定積分」を教科書とは違う角度から(リーマン和の極限として)再定義し,今度は逆に「定積分が原始関数の差である」ことを定理として導いてみようと思います.すなわち,教科書が「定積分とは原始関数の差である(定義)→定積分は面積である(定理)」という流れであったのに対し,逆に「定積分はリーマン和の極限(=面積)である(定義)→定積分は原始関数の差である(定理)」という流れで定積分というものを捉え直します.この考え方自体がとりもなおさず受験数学における求積問題の肝にもなります.

