「ビュッフォンの針問題」と呼ばれる問題です.確率の問題なのに\(\pi\)が出てくるのでなんか不思議だよねーみたいな文脈で語られることが多いと思います.今回はこの確率を実際に求めてみます.
まず,「針が交わるか交わらないか」がどんな要素に依存するかを考えてみます.それは単純に,針がどこに落ちたか,そして,落ちた針がどんな角度で横たわっているか,という2つの要素であることは容易に予測できます.
ここで,前者「針がどこに落ちたか」について少し掘り下げて考えてみましょう.「どこに」というのはいわゆる位置情報ですから,縦・横という情報を含みます.「縦方向においてどの位置にいて・横方向においてどの位置にいるか」ということですね.しかし,この問題においては横方向においてどこにいるかによって針が交わるか交わらないかというその事実が変わることはありません.
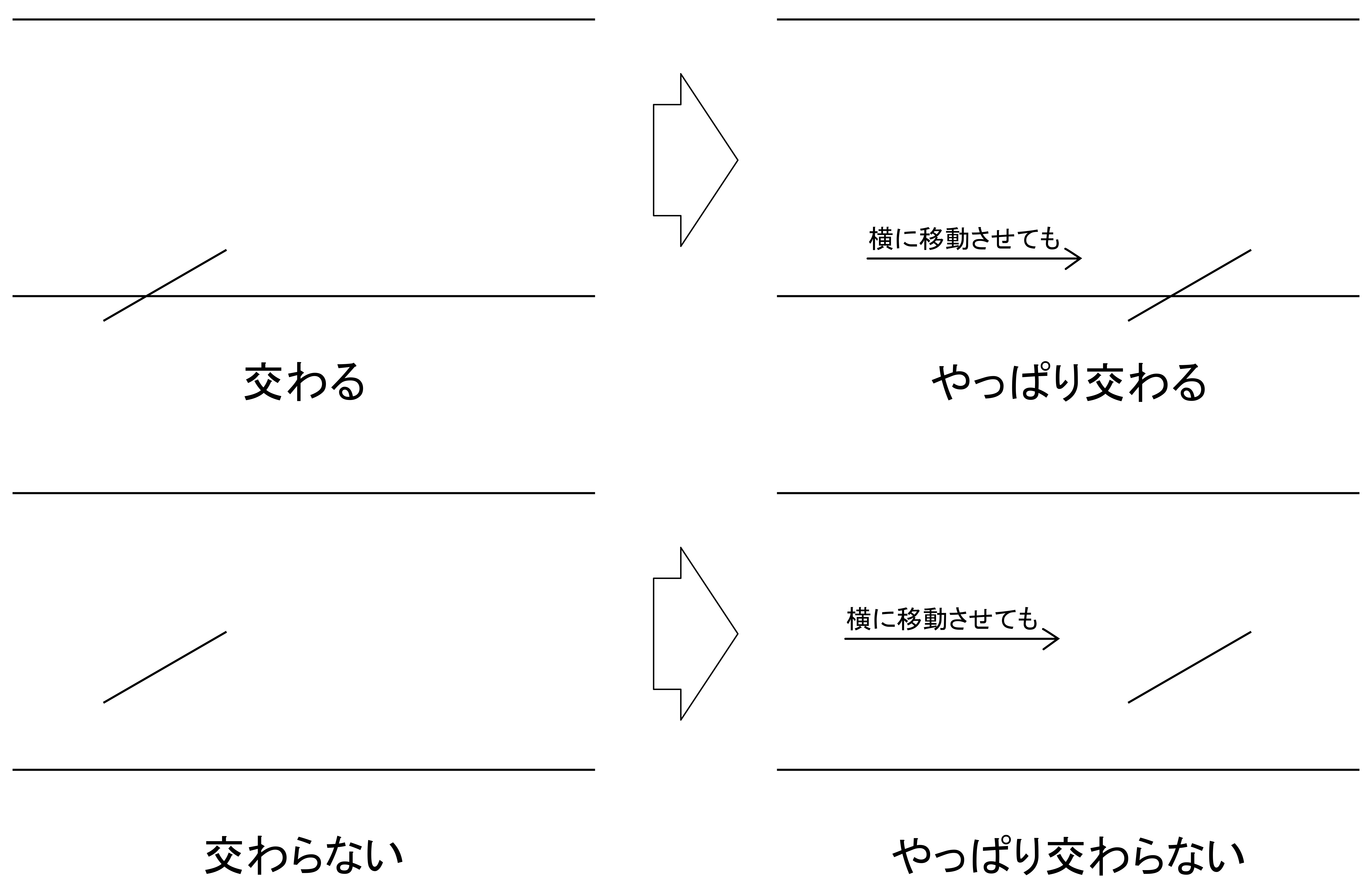
したがって「針がどこに落ちたか」に関しては縦方向のみを考えればよいことになります.
「針がどこに落ちたか(縦方向)」と「落ちた針がどんな角度で横たわっているか」をそれぞれ文字で表すことにします.
まず,「針がどこに落ちたか(縦方向)」:針の中心から,最寄りの平行線までの距離を\(d\)とします.
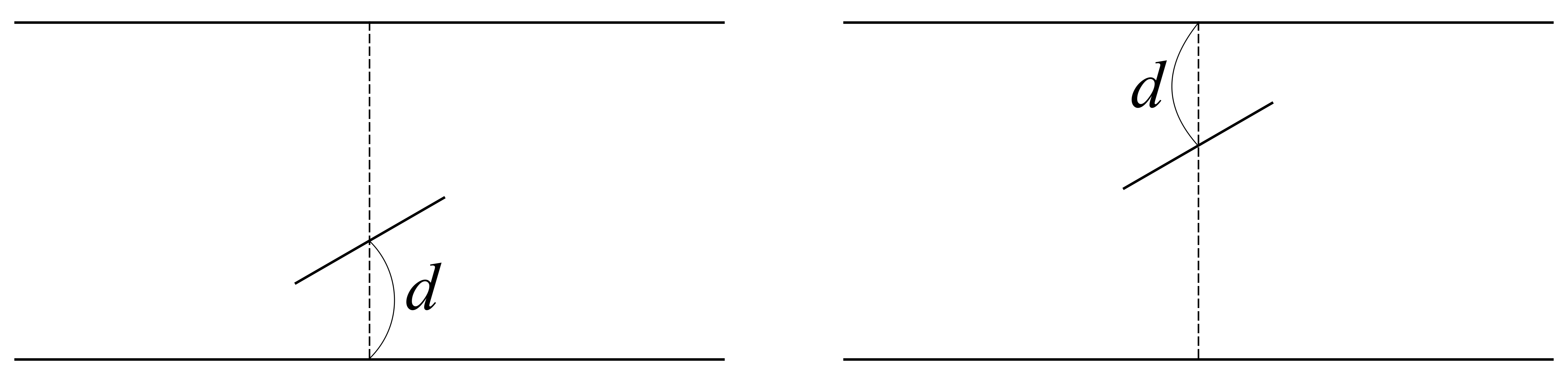
今,「最寄りの」と定義したので,この\(d\)は\(0\leq d \leq h\)です.
次に「落ちた針がどんな角度で横たわっているか」:最寄りの平行線と針のなす角を\(\theta\)とおきます.\(0\leq \theta \leq \pi\)です.

以上の準備の下に,「針が平行線と交わる」ことを数式に翻訳しましょう.図を用いて考えてみます.

このようにみると,どうやら\[d\leq l\sin\theta\]のとき針が交わることが分かります.
次に確率を求めます.
ここで,前述したように「針が平行線と交わるか交わらないか」は(平行線との縦方向の)距離\(d\)と角度\(\theta\)に依存するのでした.この二つの要素が問題なのですから,以下のような横軸が\(\theta\),縦軸が\(d\)であるような座標系を考えます.

この座標系における点のひとつひとつが,落ちた針の状況を表しています.例えば\(\left(\frac{\pi}{4},~\frac{h}{8}\right)\)なら,「最寄りの平行線からの距離が\(\frac{h}{8}\)で,その直線とのなす角が\(\frac{\pi}{4}\)」,例えば\(\left(\frac{5}{6}\pi,~\frac{3}{4}h\right)\)なら,「最寄りの平行線からの距離が\(\frac{3}{4}h\)で,その直線とのなす角が\(\frac{5}{6}\pi\)」のように.
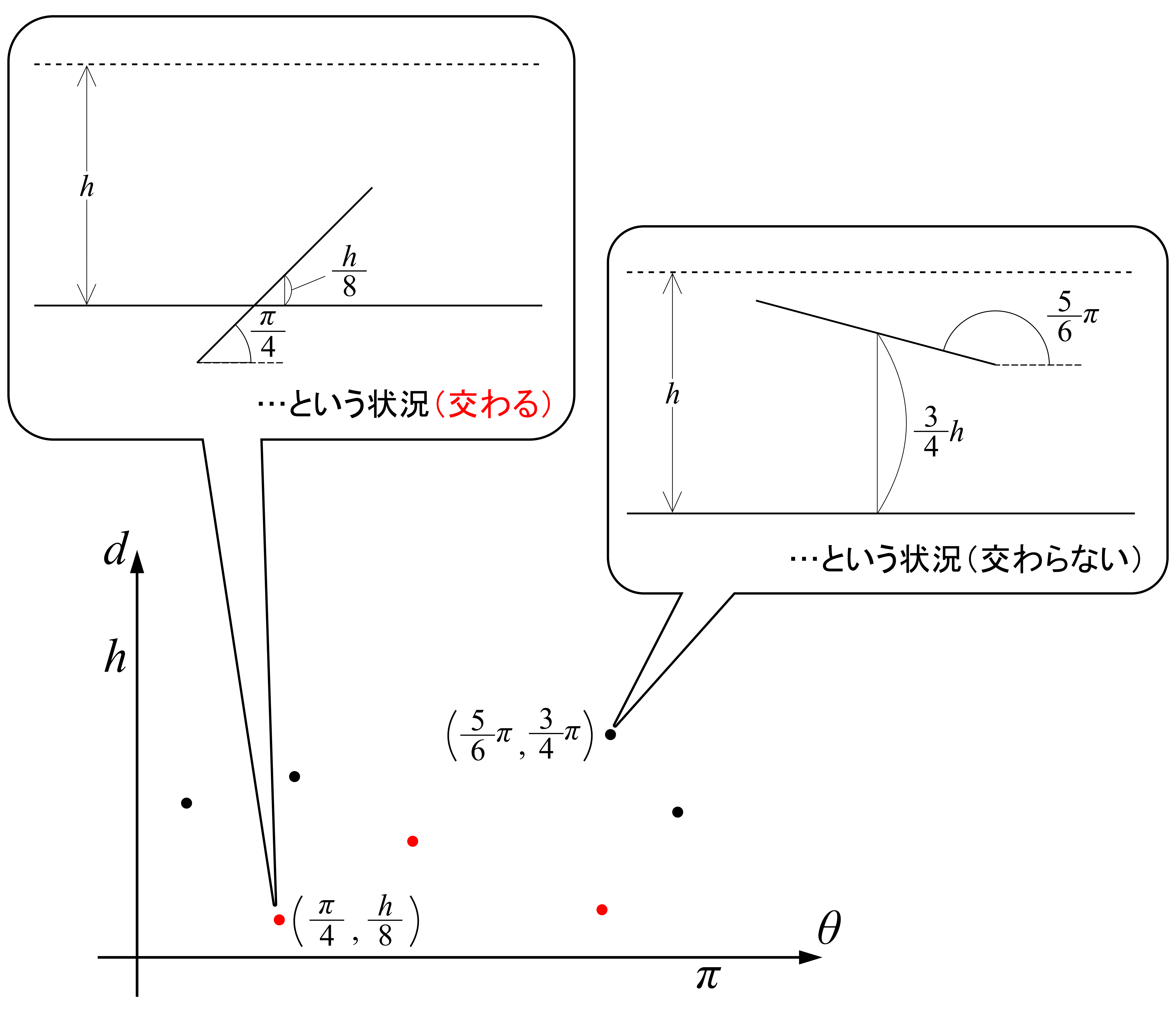
まず,針と平行線が交わるような点\((\theta,~d)\)たちを求めてみましょう.上で見たように「針と平行線が交わるような点\((\theta,~d)\)」とは,「\(d \leq l\sin\theta\)をみたす\((\theta,~d)\)」です.図示すると,下図の赤い点たちですね(イメージ).

です.この赤い部分の面積を求めると,
\[\displaystyle \int^{\pi}_0 l\sin\theta d\theta=l\Bigl[-\cos\theta\Bigl]^{\pi}_0=2l\quad\cdots(1)\]
となります.
他方,起こり得るすべての点\((\theta,~d)\)たちはどんな点たちでしょうか.今,\(\theta\)軸が\(0\leq \theta \leq \pi\),\(d\)軸が\(0\leq d \leq h\)ですから,起こり得るすべての点の集合は以下のような図になります(イメージ).
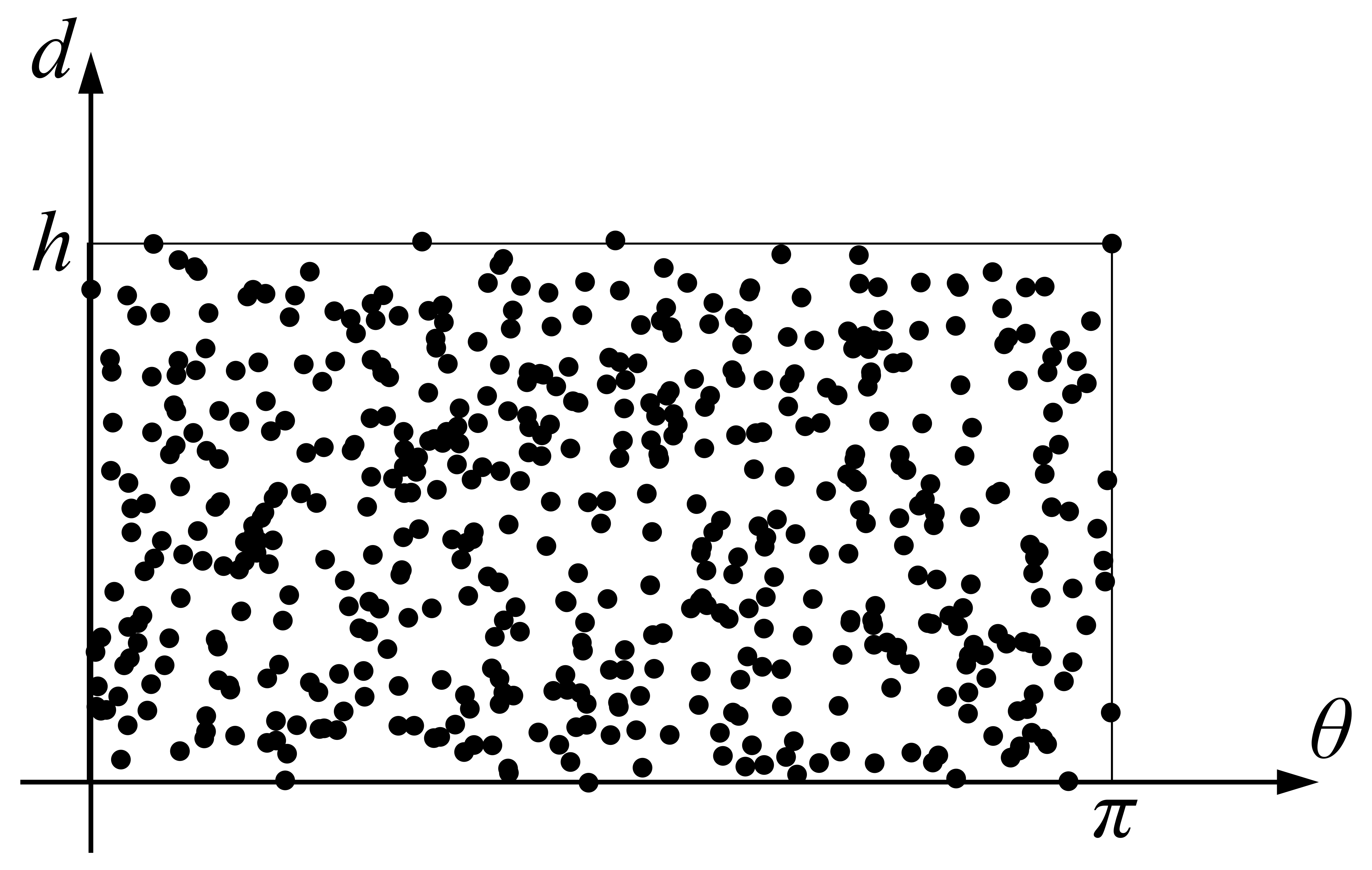
この部分の面積は\[h\times \pi=\pi h\quad\cdots(2)\]です.
以上より,題意の確率は,\((2)\)の面積を分母とし,\((1)\)の面積を分子として割合を作り,
\[\frac{\text{(1)の面積}}{\text{(2)の面積}}=\frac{2l}{\pi h}\]
となります.
以前,生徒に聞いたのですが,とあるクイズ番組で東大生がこの問題を問われた瞬間に結果を即答したそうです^^;結果を覚えていたのか,それとも・・・?

