ここに始点が揃った2つのベクトル\(\vec{a}\)と\(\vec{b}\)があります.\(\vec{a}\)による\(\vec{b}\)への落とした影となるベクトルを,「\(\vec{a}\)の正射影ベクトル」と呼びます.この\(\vec{a}\)の正射影ベクトルを求めてみましょう.

まず,\(\vec{b}\)と同じ向きの単位ベクトル\(\frac{\vec{b}}{|\vec{b}|}\)(下図青のベクトル)が1目盛りになるような軸(下図赤の軸)を設定します.このとき,正射影ベクトルの終点が指し示す場所の座標はいくらになるでしょうか.三角比の公式より,\(|\vec{a}|\cos\theta\)ですね.これは\(\theta\)が鈍角のときも成り立ちます.\[\text{正射影ベクトルの終点が指し示す座標は,}|\vec{a}|\cos\theta\text{で表される}\]
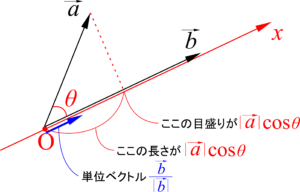
※ ここで「えっ?」と思った人は拡張された三角比の定義とそこから作られる定理(公式)が怪しい.定義を大切にしない人はこういうところで躓きます!※
したがって,単位ベクトル\(\frac{\vec{b}}{|\vec{b}|}\)に,この「座標」を掛けてやれば,正射影ベクトルが求まります.\[\text{正射影ベクトル}=\frac{\vec{b}}{|\vec{b}|}|\vec{a}|\cos\theta\]これで正射影ベクトルを表す式が手に入りました.
・・・と,上の式を公式としてもいいのですが,見た目がちょっと汚いので,もう少し手を加えてみましょう.上の単位ベクトル\(\frac{\vec{b}}{|\vec{b}|}\)を\(\vec{e}\)と表すことにして,さらに\(|\vec{a}|\cos\theta\)が
\[
\begin{align*}
|\vec{a}|\cos\theta&=|\vec{a}||\vec{e}|\cos\theta\\
&=\vec{a}\cdot\vec{e}
\end{align*}
\]
と表せることに注意すると,結局正射影ベクトルは,\[(\vec{a}\cdot\vec{e})\vec{e}\]とシンプルに記述できることになります.この結果は記憶に値します.というか常識にしておきたい知識です.なぜなら,「正射影ベクトル」が欲しくなるシチュエーションは入試その他で頻出だからです.
後日,この正射影ベクトルが使われる例を紹介してみたいと思います.

