shotasasaki – ページ 3 – 佐々木数学塾

2022年5月12日2022年5月12日

実験する

次の$2$つの条件$\mathrm{(i),(ii)}$をみたす自然数$n$について考える．

$\mathrm{(i)}~$$n$は素数ではない．
$\mathrm{(ii)}~$$l,m$を$1$でも$n$でもない$n$の正の約数とすると，必ず\[|l-m|\leq 2\]である．このとき，次の問いに答えよ．

1. $n$が偶数のとき，$\mathrm{(i),(ii)}$をみたす$n$をすべて求めよ．
2. $n$が$7$の倍数のとき，$\mathrm{(i),(ii)}$をみたす$n$をすべて求めよ．
3. $2\leq n \leq 1000$の範囲で，$\mathrm{(i),(ii)}$をみたす$n$をすべて求めよ．

（大阪大）

うーんわからない／(^o^)＼
なんかよくわからないので，実験してみます。

（考え方）

$\textbf{1.}$
偶数$2,4,6,8,\cdots$を順に調べてみます。

するとどうやら，$n$が$10$以降だと適するものが現れないのでは？と予想できます。そこで，「$n\geq 10$ならば$n$は$\mathrm{(i),(ii)}$を満たさない」という命題の証明を試みます。実際，$n=2k~(k\geq 5)$とおくと，$2$と$k$は$n(=2k)$の$1$でも$n$でもない正の約数ですが，\[|k-2|=k-2\geq 5-2 =3\]となり$(\mathrm{ii})$を満たしません。

これで$1.$の答えは$4,6,8$のみであることが分かりました。

$\textbf{2.}$
これも$1.$と同様に考えてみます。ただし$n$が偶数の場合は$1.$ですでに調べているので，これを除いて調べていきます：

すると$n$が$63$以降だと適するものが現れないのでは？と予想できます。そこで「$n\geq 63$ならば$n$は$\mathrm{(i),(ii)}$を満たさない」という命題の証明を試みると：

$n=7k~(k\geq 9)$とおく．$k=9$とき，$n=63$より正の約数は$1,3,7,9,21,63$だから$(\mathrm{ii})$を満たさない．$k \geq 11$のとき，$7$と$k$は$n(=7k)$の$1$でも$n$でもない正の約数だが，\[|k-2|=k-2\geq 11-2 =9\]となり$(\mathrm{ii})$を満たさない．

これで$2.$の答えは$35$と$49$のみであることが分かりました。

$\textbf{3}.$
上と同じように考えれば，$n$が$3$の倍数のとき，$5$の倍数のときも同じように$\mathrm{(i),(ii)}$を満たす$n$が簡単に見つかる気がします。もしそうであれば，結局$2,3,5,7$の倍数についてはすべて調べ上げたことになるので，調べるべき残りの$n$は（$\mathrm{(i)}$より$n$は素数でないことに注意すれば）$11$以上の素因数からなる合成数のみ調べればよいことが分かります（エラトステネスのふるい）。また，その合成数の因数の個数に着目すれば，因数の個数が$1$個のとき素数になるから$\mathrm{(i)}$を満たさず，因数の個数が$3$個以上のときは最小でも$11^{3}=1331$となり$1000$を超えてしまうことから，（素）因数の個数は$2$個であることが分かります。さらに，$37 \times 37 =1369>1000$より，$37$以降の素数については考える必要はありません。以上の考察から以下のように結論できます：

$n$が$3$の倍数の場合
$2,7$の倍数のときはすでに調べてあり，また$5$の倍数の場合はこのあと調べるのでこれらを除いて調べると

求める$n$は$9$のみであることが分かる（証明は上と同様なので割愛）．

$n$が$5$の倍数の場合

求める$n$は$15$と$25$のみであることが分かる（証明割愛）．
あとは素因数が$11$以上で$31$以下であり，かつその個数が$2$個である合成数のみを調べればよい．

するとそれは（$\mathrm{(ii)}$に注意して）\[11^2,13^2,17^2,19^2,23^2,29^2,31^2,11\times13,17\times19,29\times 31\]すなわち\[121,169,289,361,529,841,961,143,323,899\]のみであることがわかる．以上により求める$n$は\[4,6,8,9,15,25,35,49,121,143,169,289,323,361,529,841,899,961\]となる．

（考え方終わり）

既知の解法にはまらないとき，あるいは既知の解法に帰着しないとき（＝何をすればいいのか見通しが立たないとき），「とりあえず実験してみて，予想し，それを証明する」という姿勢はしばしば有効な気がします。（少なくとも泥臭く手を動かすだけで$2.$までは答えを導ける！）

2022年5月7日2022年5月8日

連立方程式（解の存在条件）

実数$m$を定数とする．$x$と$y$に関する連立1次方程式$\begin{cases}2x+y-2=0\\mx-y-3m+1=0\end{cases}$が$x>0$かつ$y>0$である解をもつための必要十分条件を求めよ．

（慶応大）

受験勉強を始めると最初の方で出会ってやる気を削ぐ系の問題＾＾；

解答

\begin{align*}
&~\exists x \exists y \left[\begin{cases}2x+y-2=0\\mx-y-3m+1=0\end{cases}\land x>0 \land y>0\right]\\
&~\exists x \exists y \left[\begin{cases}2x+y-2=0\\(m+2)x-3m-1=0\end{cases}\land x>0 \land y>0\right]\\
\Longleftrightarrow&~\exists x \exists y \left[2x+y-2=0 \land (m+2)x-3m-1=0 \land x>0 \land y>0 \right. \\
&\left.\land (m+2=0 \lor m+2 \neq 0)\right]\\
\Longleftrightarrow&~\exists x \exists y \left[(2x+y-2=0 \land (m+2)x-3m-1=0 \land x>0 \land y>0 \land m+2=0 )\right.\\
&\lor \left.(2x+y-2=0 \land (m+2)x-3m-1=0 \land x>0 \land y>0 \land m+2 \neq 0)\right]\\
\Longleftrightarrow&~\exists x \exists y \left[(2x+y-2=0 \land 5=0 \land x>0 \land y>0 \land m=-2) \right.\\
&\lor \left.(2x+y-2=0 \land (m+2)x-3m-1=0 \land x>0 \land y>0 \land m \neq -2)\right]\\
\Longleftrightarrow&~\exists x \exists y \left[y=-2x+2 \land x =\frac{3m+1}{m+2} \land x>0 \land y>0 \land m \neq -2)\right]\\
\Longleftrightarrow&~\exists x \exists y \left[y=-2\frac{3m+1}{m+2}+2 \land x =\frac{3m+1}{m+2} \land x>0 \land y>0 \land m \neq -2)\right]\\
\Longleftrightarrow&~\exists x \exists y \left[y=\frac{2-4m}{m+2} \land x =\frac{3m+1}{m+2} \land x>0 \land y>0 \land m \neq -2)\right]\\
\Longleftrightarrow&~\frac{2-4m}{m+2}>0 \land \frac{3m+1}{m+2}>0 \land m \neq -2\\
\Longleftrightarrow&~\frac{2-4m}{m+2}>0 \land \frac{3m+1}{m+2}>0 \land (m+2>0 \lor m+2<0)\\ \Longleftrightarrow&~ \left( \frac{2-4m}{m+2}>0 \land \frac{3m+1}{m+2}>0 \land m+2>0 \right)\\
&\lor \left(\frac{2-4m}{m+2}>0 \land \frac{3m+1}{m+2}>0 \land m+2<0\right)\\ \Longleftrightarrow&~ \left( 2-4m>0 \land 3m+1>0 \land m>-2 \right)\\
&\lor \left(2-4m<0 \land 3m+1<0 \land m<-2\right)\\
\Longleftrightarrow&~ \left( m<\frac{1}{2} \land m>-\frac{1}{3} \land m>-2 \right)\lor \left(m>\frac{1}{2} \land m<-\frac{1}{3} \land m<-2\right)\\
\Longleftrightarrow&~ m<\frac{1}{2} \land m>-\frac{1}{3} \land m>-2\\
\Longleftrightarrow&~ -\frac{1}{3} < m < \frac{1}{2}
\end{align*}

解答終

こう考えればただの（論理）計算問題なのでめっちゃ楽。

2022年4月30日2022年4月30日

tex備忘録

自分のためのノート（emathを置く場所）

コマンドプロンプトを開く（Windowsキー+r→cmdと入力，enter）
C:\Users\*****
*****の下にtexmfというフォルダを作る
コマンドプロンプトで
kpsewhich –expand-path=$TEXMF
と入力しenter
;の数+1=1ならそこを★とおき，6.へ
;の数+1>1ならコマンドプロンプトで
kpsewhich –expand-path=$TEXMFHOME
と入力しenter
返ってくるもの（3.の結果でみた〇;△;□のどれか）を★とおく
コマンドプロンプトで
kpsewhich –progname=platex jarticle.cls
と入力しenter
…/texmf/☆☆☆/☆☆☆/base/…
または
…/texmf-dist/☆☆☆/☆☆☆/base/…
と表示される
置き場所は
★/☆☆☆/☆☆☆/misc/emath
（フォルダmisc,emathは新規に作成する）
ここにsty.zipを解凍して得られるファイルをすべて置く

2022年4月20日2023年10月12日

合同式の応用

$10^{10}$を$2020$で割った余りを求めよ。
$100$桁の正の整数で各位の数の和が$2$となるもののうち，$2020$で割り切れるものの個数を求めよ。

（一橋大）

解答

$2020$を法として考える．以下，$\mod 2020$を省略して記述する．
$10000\equiv10000+2020\cdot(-5)\equiv-100$であるから，
\begin{align*}
10^{10}\equiv&10^2\cdot(10^4)^2\\
\equiv &10^2\cdot(-100)^2\\
\equiv &10^2\cdot10000\\
\equiv &10^2\cdot(-100)\\
\equiv &-10000\\
\equiv &-(-100)\\
\equiv &100
\end{align*}

ゆえに$10^{10}\equiv100$（$1.$の答え）

$100$桁の正の整数で各位の数の和が$2$であるような数は
\begin{align*}
\mathrm{(i)}\quad &2\underbrace{0\cdots0}_{99\text{個}}=2\times10^{99}\\
\mathrm{(ii)}\quad &1\underbrace{0\cdots01\overbrace{0\cdots0}^{k\text{個}}}_{99\text{個}}=10^{99}+10^k\quad(0\leq k \leq 98)
\end{align*}のいずれかである．

$\mathrm{(i)}$のとき
$1.$により$10^{10}\equiv10^2$であることに注意して，
\begin{align*}
2\times10^{99}\equiv&2\cdot10^{9}\cdot(10^{10})^9\\
\equiv&2\cdot10^{9}\cdot(10^{2})^9\\
\equiv&2\cdot 10^{27}\\
\equiv&2\cdot(10^{10})^2\cdot10^7\\
\equiv&2\cdot(10^{2})^2\cdot10^7\\
\equiv&2\cdot10^{11}\\
\equiv&2\cdot10^{10}\cdot10\\
\equiv&2\cdot10^{2}\cdot10\\
\equiv&2000\\
\end{align*}ゆえにこの数は$2020$で割り切れない．

$\mathrm{(ii)}$のとき
$10^{99}+10^{k}\equiv 1000 + 10^{k}$より（なぜならば$\mathrm{(i)}$の途中過程により$10^{99}\equiv1000$），$1000+10^k\equiv 0(\Leftrightarrow 10^{k}\equiv -1000)$を満たす$k~(0\leq k \leq 98)$の個数を調べればよい．$k$の値は高々$99$個なので，実際に調べてみると（やる気），

$1,10$から始まり，$100,1000,-100,-1000$と繰り返すことがわかる．したがって，$99=2+4\times 24+1$により求める個数は$24$個とわかる．（$2.$の答え）

解答終

2022年4月18日2022年4月18日

必要条件を追う

$a_0,a_1,a_2$を有理数とし，$f(x)=a_0+a_1x+\frac{a_2}{2}x(x-1)$とする．$1$つの整数$n$に対して，$f(n),f(n+1),f(n+2)$が整数ならば，$a_0,a_1,a_2$は整数であることを示せ．

（中央大）

示すべきは必要条件であること，つまり十分性（逆が言えるか？）を考える必要がないことに注意します。これは細かいことを考えず手元にある道具（仮定）を好き勝手にいじり倒して結論が言えればその時点で証明終わりということなので気楽です：\[f(n),f(n+1),f(n+2)\in\mathbb{Z}\overset{\text{ひつよう！}}{\Longrightarrow} a_0,a_1,a_2 \in\mathbb{Z}\]
とりあえず，$f(n)$と$f(n+1)$の$n$と$n+1$は連番なので，差をとってみたらどうか？と思いつきます。（邪魔者がもろもろ消えそうだから）\begin{align*}
&~f(n+1)-f(n)\in \mathbb{Z}\\
\Longleftrightarrow&~\left(a_0+a_1(n+1)+\frac{a_2}{2}(n+1)n\right)\\
&~-\left(a_0+a_1n+\frac{a_2}{2}n(n-1)\right)\in \mathbb{Z}\\
\Longleftrightarrow&~a_1+a_2n \in \mathbb{Z}\tag{1}
\end{align*}なんかうまくいきそうなので，$f(n+2)-f(n+1)$も同様に計算すると，\[f(n+2)-f(n+1)\in \mathbb{Z}\Longleftrightarrow a_1+a_2n+a_2 \in \mathbb{Z}\tag{2}\]が得られます。$(1)$と$(2)$において$a_1+a_2n$が共通していることに着目して$a_2$が整数であることがわかり，またこれと$(1)$により芋づるで$a_1$が整数であることが言えます。残りは$a_0$ですが，これは$f(n)=a_0+a_1+\frac{a_2}{2}n(n-1)\in\mathbb{Z}$であること，すでに示したように$a_1,a_2\in \mathbb{Z}$であること，そして$n(n-1)$は連続数だから偶数したがって$\frac{a_2}{2}n(n-1)\in\mathbb{Z}$であることからいうことができます。（証明終）

とりあえず必要性を追うという方針で証明してみましたが，こうしてみると次のように同値変形できることに気づきます：

証明

\begin{align*}
&~f(n),f(n+1),f(n+2)\in \mathbb{Z}\\
\overset{(\ast)}{\Longleftrightarrow}&~f(n+1)-f(n)\in\mathbb{Z} ,f(n+2)-f(n+1)\in\mathbb{Z},f(n)\in\mathbb{Z}\\
\Longleftrightarrow&~a_1+a_2n \in \mathbb{Z},a_1+a_2n+a_2\in\mathbb{Z},a_0+a_1+\frac{a_2}{2}n(n-1)\in\mathbb{Z}\\
\Longleftrightarrow&~a_1+a_2n \in \mathbb{Z},a_2\in\mathbb{Z},a_0+a_1+\frac{a_2}{2}n(n-1)\in\mathbb{Z}\\
\Longleftrightarrow&~a_1\in \mathbb{Z},a_2\in\mathbb{Z},a_0+a_1+\frac{a_2}{2}n(n-1)\in\mathbb{Z}\\
\Longleftrightarrow&~a_1\in \mathbb{Z},a_2\in\mathbb{Z},a_0\in\mathbb{Z}
\end{align*}
証明終

$(\ast)$において，\begin{align*}
&~f(n),f(n+1),f(n+2)\in \mathbb{Z}\\
\Longrightarrow&~f(n+1)-f(n)\in\mathbb{Z} ,f(n+2)-f(n+1)\in\mathbb{Z}
\end{align*}ですが，$f(n)\in\mathbb{Z}$を加えることで$\Leftarrow$も言え，上のように同値になるというカンジです。

2022年4月13日2024年2月27日

絶対値を含む方程式・不等式（その1）

新高１生向け。絶対値を含む方程式・不等式おいて，「場合分け」をし，「（得た結果について，場合分けで行った）条件を満たすかどうかを確認」または「共通部分」をとりました。以下はそこで「？」と思った人向けの話です。教える側としても一般的な「場合分け」で説明しているとどこか後ろめたさを感じるのでここにノートしておきたいと思います。

まず各種公式を証明します。$c>0$とします。

\begin{align*}
&(1)\quad |x|=c \Longleftrightarrow x=\pm c\\
&(2)\quad |x| < c \Longleftrightarrow -c < x < c\\
&(3)\quad |x| > c \Longleftrightarrow x < -c \lor c < x
\end{align*}

$(1)$の証明

\begin{align*}
&|x|=c\\
\Longleftrightarrow~ & |x|=c \land (x \geq 0 \lor x < 0)\\
\Longleftrightarrow~ & (|x|=c \land x \geq 0) \lor (|x|=c \land x < 0)\\
\Longleftrightarrow~ & (x=c \land x \geq 0) \lor (-x=c \land x < 0)\\
\Longleftrightarrow~ & (x=c \land x \geq 0) \lor (x=-c \land x < 0)\\
\Longleftrightarrow~ & (x=c \land c \geq 0) \lor (x=-c \land -c < 0)\\
\Longleftrightarrow~ & (x=c \land \top) \lor (x=-c \land \top)\\
\Longleftrightarrow~ & x=c \lor x=-c\\
\Longleftrightarrow~ & x=\pm c
\end{align*}

証明終

$(2)$の証明

\begin{align*}
&|x| < c\\
\Longleftrightarrow~ & |x| < c \land (x \geq 0 \lor x < 0)\\
\Longleftrightarrow~ & (|x| < c \land x \geq 0) \lor (|x| < c \land x < 0)\\
\Longleftrightarrow~ & (x < c \land x \geq 0) \lor (-x < c \land x < 0) \\
\Longleftrightarrow~ & (0 \leq x < c) \lor (-c < x < 0) \\
\Longleftrightarrow~ & -c < x < c
\end{align*}

証明終

$(3)$の証明

\begin{align*}
&|x| > c\\
\Longleftrightarrow~ & |x| > c \land (x \geq 0 \lor x < 0)\\ \Longleftrightarrow~ & (|x| > c \land x \geq 0) \lor (|x| > c \land x < 0)\\ \Longleftrightarrow~ & (x > c \land x \geq 0) \lor (-x > c \land x < 0) \\
\overset{(\ast)}{\Longleftrightarrow}~ & c <x \lor x < -c\\
\Longleftrightarrow~ & x < -c \lor c <x\\
\end{align*}

証明終

$(\ast)$の理解：
例えば，一般に$A\land B \Rightarrow A$ですから$x > c \land x \geq 0 \Rightarrow x > c$，逆に$x > c$であるとき，$c > 0$が議論の大前提であったことを思い出すと$x > 0$であることすなわち$x \geq 0$が言え，$x > c \land x \geq 0 \Leftarrow x > c$が得られます。

以上の考察をそのまま問題に適用してみます。

次の方程式・不等式を解け．
\begin{align*}
&(1)\quad|x+4|=3x\\
&(2)\quad|2x+1| < x + 5\\
&(3)\quad 4x^2+5x-12\leq 3|x|
\end{align*}

$(1)$の解答

$(2)$の解答

\begin{align*}
&|2x+1| < x + 5\\
\Longleftrightarrow~ & |2x+1| < x + 5 \land (2x+1 \geq 0 \lor 2x+1 < 0)\\
\Longleftrightarrow~ & (|2x+1| < x + 5 \land 2x+1 \geq 0) \lor (|2x+1| < x + 5 \land 2x+1 < 0)\\
\Longleftrightarrow~ & \left( 2x+1 < x + 5 \land x \geq -\frac{1}{2} \right) \lor \left( -2x-1 < x + 5 \land x < -\frac{1}{2}\right)\\
\Longleftrightarrow~ & \left( x < 4 \land x \geq -\frac{1}{2} \right) \lor \left( x > -2 \land x < -\frac{1}{2} \right) \\
\Longleftrightarrow~ & \left( -\frac{1}{2} \leq x < 4 \right) \lor \left(-2 < x < -\frac{1}{2}\right)\\
\Longleftrightarrow~ & -2 \leq x < 4
\end{align*}

解答終

$(3)$の解答

…ちなみに教科書等では上の公式$(3)$を$x < -r,r < x$と「,（カンマ）」と書いていますがこのカンマは「または」のカンマです。教科書は「かつ」も「または」をどちらも「，（カンマ）」で略記しているので注意が必要です。

2022年4月7日

三角形の成立条件

\begin{align*}
&|b-c| < a < b+c\\
\Longleftrightarrow~& |b-c| < a \land a < b+c\\ \Longleftrightarrow~& -a < b-c < a \land a < b+c\\ \Longleftrightarrow~& -a < b-c \land b-c < a \land a < b+c\\ \Longleftrightarrow~& c < a+b \land b < a+c \land a < b+c \end{align*} なのでどっち使ってもOKです。

2022年3月30日2022年3月30日

値域の問題

実数$a,b,c$が$a+b+c=a^2+b^2+c^2=1$を満たすとする．$c$のとりうる値の範囲を求めよ．

「☆という値をとる」という主張を「その値☆を実現するような★が存在する」と言い換えます。あとはそれを機械的に処理するだけ。

解答

\begin{align*}
&\text{$c$が$k$という値をとる}\\
\Longleftrightarrow&~\exists a\in \mathbb{R}\exists b\in \mathbb{R}[a+b+k=a^2+b^2+k^2=1]\\
\Longleftrightarrow&~\exists a\in \mathbb{R}\exists b\in \mathbb{R}[a+b+k=1 \land a^2+b^2+k^2=1]\\
\Longleftrightarrow&~\exists a\in \mathbb{R}\exists b\in \mathbb{R}[b=1-a-k \land a^2+b^2+k^2=1]\\
\Longleftrightarrow&~\exists a\in \mathbb{R}[a^2+(1-a-k )^2+k^2=1]\\
\Longleftrightarrow&~\exists a\in \mathbb{R}[a^2-(1-k )a+k^2-k=0]\\
\Longleftrightarrow&~(1-k )^2-4(k^2-k)\geq 0\\
\Longleftrightarrow&~3k^2-2k-1\leq 0\\
\Longleftrightarrow&~-\frac{1}{3}\leq k \leq 1\\
\end{align*}

解答終

2022年3月22日2022年4月12日

積の和

実数$x,y$が$|x|\leq 1$と$|y| \leq 1$を満たすとき，不等式\[0 \leq x^2+y^2-2x^2y^2+2xy \sqrt{1-x^2} \sqrt{1-y^2}\leq 1\]が成り立つことを示せ．

（大阪大学文系）

積の和の形$ax+by$を$\left(\begin{array}{c} a \\ b \\ \end{array}\right)\cdot\left(\begin{array}{c} x \\ y \\ \end{array}\right)$とみると事態が好転することが少なくない気がします。

証明

$2xy \sqrt{1-x^2} \sqrt{1-y^2}$という項に着目し，中辺は$\left(y\sqrt{1-x^2}+x\sqrt{1-y^2}\right)^2$の展開式ではないかと疑う．実際，展開してみると\begin{align*}
&\left(y\sqrt{1-x^2}+x\sqrt{1-y^2}\right)^2\\
=~&y^2(1-x^2)+2xy\sqrt{1-x^2}\sqrt{1-y^2}+x^2(1-y^2)\\
=~&x^2+y^2-2x^2y^2+2xy \sqrt{1-x^2} \sqrt{1-y^2}
\end{align*}ゆえに\[x^2+y^2-2x^2y^2+2xy \sqrt{1-x^2} \sqrt{1-y^2}\geq 0\]を得る．また，
\begin{align*}
&y\sqrt{1-x^2}+x\sqrt{1-y^2}\\
=&~\left(\begin{array}{c} y \\ x \\ \end{array}\right)\cdot\left(\begin{array}{c} \sqrt{1-x^2} \\ \sqrt{1-y^2} \\ \end{array}\right)\\
=&~\sqrt{x^2+y^2}\sqrt{1-x^2+1-y^2}\cos \theta\\
=&~\sqrt{x^2+y^2}\sqrt{2-(x^2+y^2)}\cos \theta\\
=&~\sqrt{2(x^2+y^2)-(x^2+y^2)^2}\cos \theta\\
\end{align*}より
\begin{align*}
&-\sqrt{2(x^2+y^2)-(x^2+y^2)^2}\leq y\sqrt{1-x^2}+x\sqrt{1-y^2} \leq \sqrt{2(x^2+y^2)-(x^2+y^2)^2}\\
\Longleftrightarrow&~\left|y\sqrt{1-x^2}+x\sqrt{1-y^2}\right|\leq\sqrt{2(x^2+y^2)-(x^2+y^2)^2}\\
\Longleftrightarrow&~\left(y\sqrt{1-x^2}+x\sqrt{1-y^2}\right)^2\leq 2(x^2+y^2)-(x^2+y^2)^2
\end{align*}
ここで$x^2+y^2=t$とおくと，$0\leq t \leq 2$より
\begin{align*}
2t-t^2=-(t-1)^2+1\leq 1
\end{align*}であるから\[\left(y\sqrt{1-x^2}+x\sqrt{1-y^2}\right)^2 \leq 1\]すなわち\[x^2+y^2-2x^2y^2+2xy \sqrt{1-x^2} \sqrt{1-y^2}\leq 1\]を得る．

証明終

昔こういった手法を「そんなものは受験テクニックだ！」と言ってやたら否定する人がいたけど高校数学や受験数学で「テクニック」と呼ばれるものが大学数学で再登場するということが少なくない気がする。（てか，それが元ネタ？）実際，上の\[a_1x_1+a_2x_2+\cdots+a_n x_n\]を$1$次結合といい，上でしたような変形は大学で学ぶ線型代数学ではよく見られるものです。

2022年3月21日2022年5月13日

中学数学

生徒（中学生）の考査で，論理的にはあっているのに０点にされている証明があった。…何でこれバツにされたの？？と聞くと「（証明自体はあっていても冒頭に）『$\triangle{ABC}$と$\triangle{DEF}$において』の一言がないから」とのこと…

「$\triangle{ABC}$と$\triangle{DEF}$において」という一言は「これから私はこの二つの三角形に着目しますよ」という記述する側が読み手の読み易さのために入れるいわば「気遣い」の一言に過ぎず，論理そのものには関わる部分ではないから，証明の記述としてはあってもなくてもいい（「$\triangle{ABC}$と$\triangle{DEF}$において（$\triangle{ABC}$と$\triangle{DEF}$に着目している）」という文は$\triangle{ABC}\equiv\triangle{DEF}$という結論を示すための仮定そのものではない）と僕は理解しているが，違うのだろうか？？

もしかしたら幾何学の世界では証明の冒頭に「$\triangle{ABC}$と$\triangle{DEF}$において」と書かなくてならないという「型」みたいなものがあるのかな？と思い（んなもんあるわけない）手元の初等幾何の本を見てみた。

定理

$1^{\circ})$ 平行四辺形の対辺は等しい．
$2^{\circ})$ 平行四辺形の対角は等しい．

証明

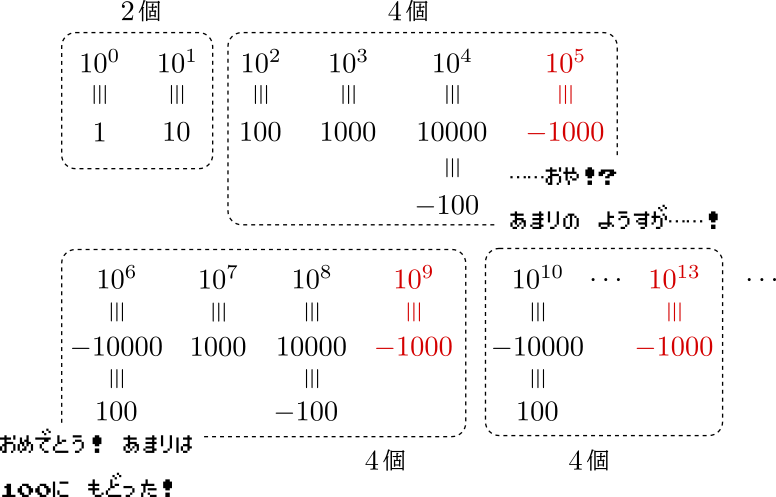
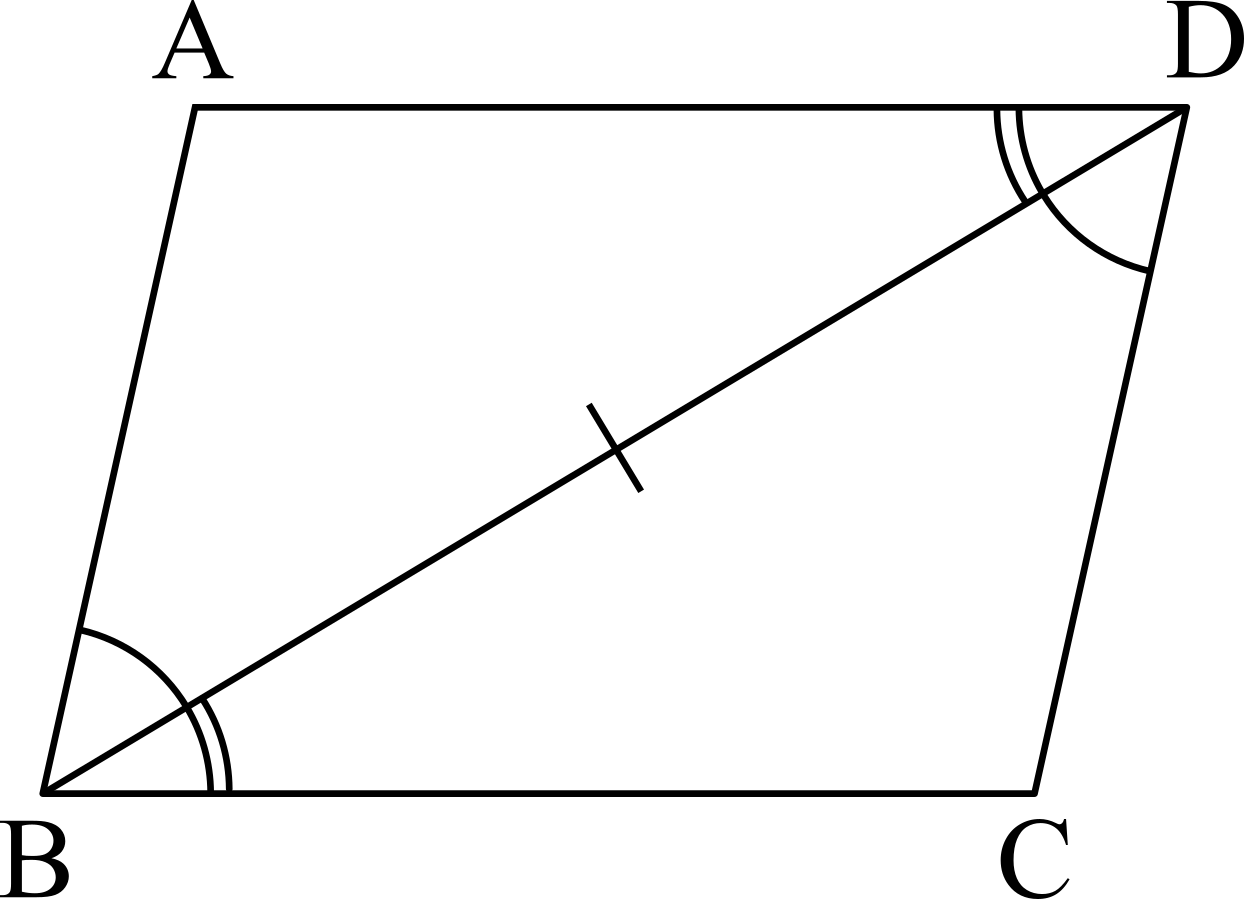右の図の四角形$ABCD$において\[AB\parallel DC,~AD\parallel BC\]とします．平行な二直線が第三の直線と交わってなす錯角は等しいから（63ページ，定理4.2），\[\angle{ABD}=\angle{CDB},~\angle{ADB}=\angle{CBD}\]となります．ゆえに，一辺両端角の合同定理（42ページ，定理3.2）により，\[\triangle{ABD}\equiv \triangle{CDB}\]ゆえに\[AB=CD,~AD=CB,~\angle{A}=\angle{C}\]

（証明終）

小平邦彦．幾何への誘い．岩波書店，2015

$\triangle{ABD}\equiv \triangle{CDB}$を示すにあたり「$\triangle{ABD}$と$\triangle{CDB}$において」なんてひとことは出てきてない。小平先生のこの証明も中学校の先生によれば０点なんだろうか。

他にも三角形がが合同であることを示すにあたり，辺の長さが等しい，ということを明示するのに$AE=AD$が正解で$AE=DA$と書くと減点対象だったりと，なんかよく分からん世界です。