証明
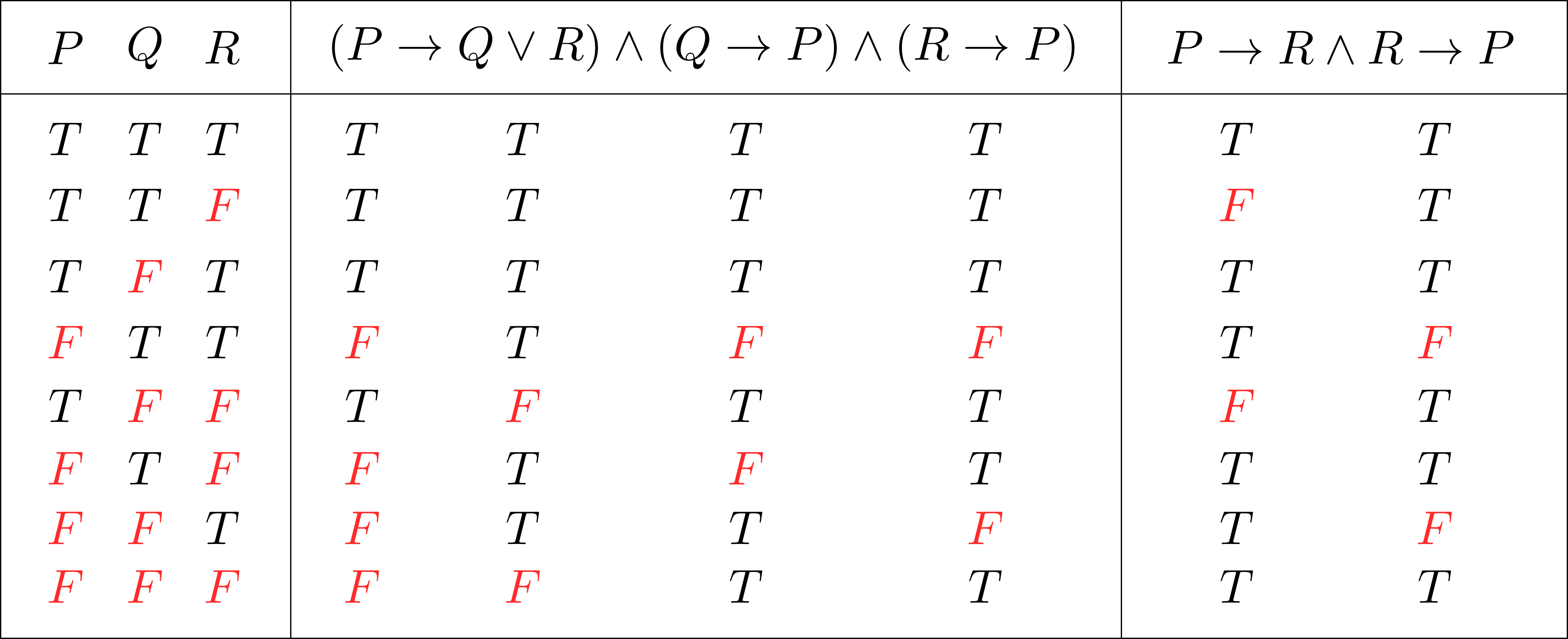


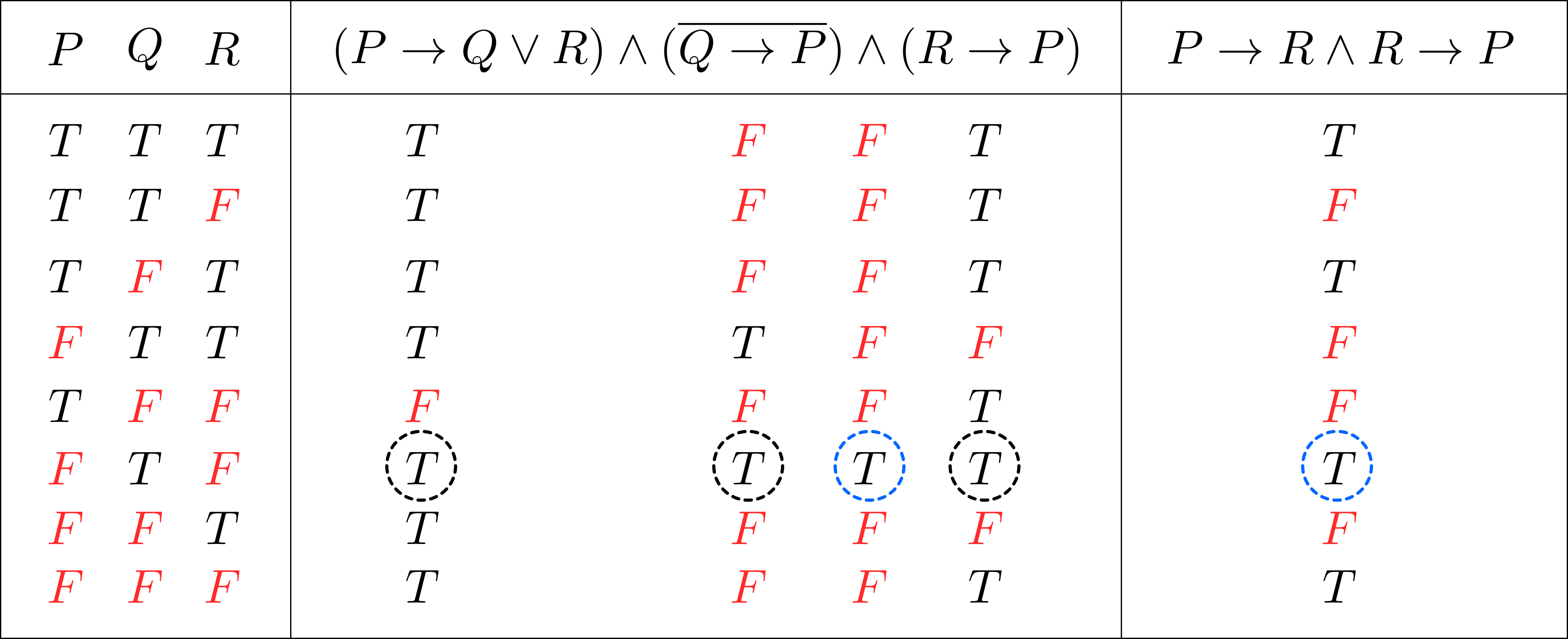
\(P\Rightarrow Q \lor R,\overline{Q\Rightarrow P},R \Rightarrow P\)となる行,すなわち\(P\rightarrow Q \lor R,\overline{Q\rightarrow P},R \rightarrow P\)が真となる行(上から6行目)に着目すると,\((P\rightarrow Q \lor R) \land \overline{Q\rightarrow P} \land (R \rightarrow P)\)と\(P \leftrightarrow R\)の真理値(青〇)が一致している.したがって\[(P\Rightarrow Q \lor R) \land \overline{Q\Rightarrow P} \land (R \Rightarrow P)\Longrightarrow~(P \Leftrightarrow R)\]を得る.
証明終
(関連:2次方程式の共通解問題(その2))


