タグ: 数学Ⅰ

投稿日:

\(p \rightarrow q \Longleftrightarrow \overline{p}\lor q\)

極めてよく使う同値変形\[p \rightarrow q \Longleftrightarrow \overline{p}\lor q\]を確認してみましょう．真理値表を書いて調べてみます．実際に紙の上で調べる際の手順を再現してみます（一緒に書いてみてくださいね）．

まず，命題\(p\)と命題\(q\)の真偽の組合せは以下のように\(2\times 2\)通りあります．


次に，\(p \rightarrow q\)について調べたいので，最上行にそれを書きこみましょう．\(\rightarrow\)の定義から，その真理値は以下のように書けます（\(p\)が真で\(q\)が偽であるときのみ，\(p \rightarrow q\)は偽であるのでした）．


次に，調べたい\(\overline{p}\lor q\)を同じく最上行に書き込みます．


いきなり\(\overline{p}\lor q\)の真理値を書き込むのは難しいので，順を追って書き込むことにします．まずは\(\overline{p}\)から．これは簡単ですね．定義により，次のように書き込めます．


次に\(q\)．これはそのまま．


いよいよ\(\overline{p}\lor q\)の真理値．\(\lor\)の定義により，


さて，\(p \rightarrow q\)と\(\overline{p}\lor q\)の真理値をながめてみましょう．真理値が一致しています．すなわちこの二つの命題は同値であることが確認できます．

※ 本来ならば，\(p,~\overline{p},~\overline{p}\lor q\)の真理値はそれぞれ別々の列に書くのが正しい（と思う）のですが，面倒なので上のように略記しています．

投稿日:

平行移動の公式

平行移動の公式
\(y=ax^2\)のグラフを，\(x\)軸方向に\(p\)，\(y\)軸方向に\(q\)だけ平行移動した放物線は\[y=a(x-p)^2+q\]である．

この公式を教科書ではどのように説明しているかというと…

\(y=2x^2,~y=2x^2+3\)という具体例を持ち出してこの二者の関係を調べて（表または実際にグラフを描き），そこから\(y=2x^3+3\)のグラフは，\(y=2x^2\)のグラフを\(y\)軸方向に\(3\)だけ平行移動したものである，と結論し，
\[\downarrow\]
\(y=2x^2,~y=2(x-3)^2\)という具体例を持ち出し，表からこの二者の関係を調べて\(y=2(x-3)^3\)のグラフは，\(y=2x^2\)のグラフを\(x\)軸方向に\(3\)だけ平行移動したものである，と結論し，
\[\downarrow\]
そしてこの二つから上の公式を結論しています（詳しくはお手持ちの教科書参照）．

この公式に限らず，高校の教科書は\[\textbf{具体例}\rightarrow\textbf{一般論}\]という書き方をしています．「この場合はこうだよね～，あの場合もこうだよね～，ということは一般にこう言えるよね～」という論法ですね．これで「ああなるほど！」と思えればいいんでしょうけど，なんか騙された気がするひとも少なくないはず．実際，数学を学ぶ姿勢としてはこれだけでは納得できない（しない）方がむしろよいと思います．二，三の例が正しいからとしって他の例も正しいとは限りませんからね．

というわけで証明（※注意 pdfファイルです）

いわゆる「教科書通り」にやるとこういったことを飛ばすことになるんですが，それが「数学を勉強している」ことになるんでしょうか…？もっとも，こういった話はテストに出ない（出せない）わけですからやったところでスコアにはならない．その意味においてはやる意味がない，のかもしれませんが…．でも，天下り的に与えられた解決策をただ覚えるだけではないある意味メタ的な能力を培うことも数学を学ぶ重要な意義のひとつだと思うんですが．まあ，教える側，教わる側共々様々な事情・制約がありますから，難しい問題です．

 

投稿日:

「ならば」の否定

問題
\(a,~b\)を有理数とするとき，\(\sqrt{3}\)が無理数であることを用いて，「\(a+b\sqrt{3}=0\)ならば\(a=0\)かつ\(b=0\)」であることを証明せよ．

定番問題です。解答を見ると，次のように始まります。

\(b\neq 0\)とすると…

 

賢明な生徒であればここで「背理法かな？」気付くはず。それは正しいです。では，与えられた命題「\(a+b\sqrt{3}=0\)ならば\(a=0\)かつ\(b=0\)」の否定が「\(b\neq 0\)」ということでしょうか？…うーん明らかに違う気が。。

「\(a+b\sqrt{3}=0\)ならば\(a=0\)かつ\(b=0\)」の否定がどうなるかに注意しつつ，証明を作ってみます。与えられた命題は論理記号を用いて「\(a+b\sqrt{3}=0\Longrightarrow a=0\land b=0\)」と書けることに注意して，

証明（その１）

\[\overline{ a+b\sqrt{3}=0 \Longrightarrow a=0 \land b=0}\]と仮定する．
\begin{align}
&\overline{ a+b\sqrt{3}=0 \Longrightarrow a=0 \land b=0}\\
\Longleftrightarrow~ &\overline{\overline{a+b\sqrt{3}=0} \lor (a=0 \land b=0)}&(\Rightarrow \text{の定義})\\
\Longleftrightarrow~ &a+b\sqrt{3}=0 \land \overline{a=0 \land b=0}&(\text{ドモルガンの法則})\\
\Longleftrightarrow~ &a+b\sqrt{3}=0 \land (a \neq 0 \lor b \neq 0)&(\text{ドモルガンの法則})\\
\Longleftrightarrow~ &(a+b\sqrt{3}=0 \land a \neq 0 ) \lor (a+b\sqrt{3}=0 \land b \neq 0)&(\text{分配法則})\\
\Longleftrightarrow~ &\left(1+\frac{b}{a}\sqrt{3}=0 \land a \neq 0 \right) \lor \left(\frac{a}{b}+1\sqrt{3}=0 \land b \neq 0\right)\\
\Longleftrightarrow~ &\left(\frac{-3b}{a}=\sqrt{3} \land a \neq 0 \right) \lor \left(-\frac{a}{b}=\sqrt{3} \land b \neq 0\right)\\
\Longleftrightarrow~ &\bot \lor \bot\\
\Longleftrightarrow~ &\bot
\end{align}

したがってもとの命題は正しい．

証明終

\(\bot\)は矛盾命題を表します。

…では，模範解答の「\(b\neq 0\)とすると～」は一体何をしているのでしょうか？これはおそらく以下のようだと思われます：

証明（その２）

\[
\begin{align}
&a+b\sqrt{3}=0 \Rightarrow b=0 \\
\overset{(\ast)}\Longleftrightarrow~&a+b\sqrt{3}=0 \Rightarrow a+b\sqrt{3}=0 \land b=0 \\
\Longleftrightarrow~ &a+b\sqrt{3}=0 \Rightarrow a=0 \land b=0
\end{align}
\]
であるから，\[a+b\sqrt{3}=0 \Rightarrow b=0\]を示せばよい．この命題を否定すると\[a+b\sqrt{3}=0 \land b\neq 0\]であるが，
\[a+b\sqrt{3}=0 \land b\neq 0\Longleftrightarrow\sqrt{3}=-\frac{a}{b} \land b\neq 0\]これは矛盾である．

証明終

上の証明における\((\ast)\)は，（直観的にはまあ明らか，ではありますが）\[(P\Rightarrow Q) \Longleftrightarrow (P\Rightarrow P \land Q)\]という論理式によります。いずれにしても，ならば（含意）の否定というものを学んでいない以上，上のような証明は作りようがない。いきなり「\(b \neq 0\)とする」なんて言われても納得しようがないし，安易に納得してはいけない。ちなみにこの解答の脚注にはこんな一言が載っています。「結論が\(p\)かつ\(q\)という命題を背理法を用いて証明するときは\(\overline{p}\)または\(\overline{q}\)のみを仮定して矛盾を導けばよい」…でもそうすべき理由とその方針が正しい理由は？

まあ，ある程度はブラックボックス化するのはやむを得ないとはいえ，ここは端折るところではないのでは…と思います。さもなければそもそも\(P\Rightarrow Q \land R\)なんて命題の証明なんて取り扱わないで欲しい。生徒に説明するとき誤魔化すハメになりほんと迷惑極まりない。

 

投稿日:

「でない」「かつ」「または」「ならば」の定義

最初に「命題」「条件」という言葉の確認から．

命題：正しいか正しくないかを一意的に判定できる主張
条件：変数（変項ともいいます）を含む命題

これらは高校生は数学Ⅰで既習だと思います．

以下，\(p,~q\)を命題とします．\(\overline{p},~p\land q,~p \lor q,~p\rightarrow q\)を改めて定義します．

定義

\(p\land q\)
\(p\)と\(q\)が両方真のときのみ真で，その他の場合はすべて偽となるような命題．この命題を「\(p\)かつ\(q\)」と呼び，\(p \land q\)と表す．

\(p \lor q\)
\(p\)と\(q\)が両方偽ときのみ偽で，その他の場合はすべて真となるような命題．この命題を「\(p\)または\(q\)」と呼び，\(p \land q\)と表す．

\(\overline{p}\)
\(p\)が真のときに偽で\(p\)が偽のときに真となるような命題．この命題を「\(p\)でない」あるいは「\(p\)の否定」と呼び，\(\overline{p}\)あるいは\(\lnot{p}\)と表す．

\(p\rightarrow q\)
\(p\)が真で\(q\)が偽のときのみ偽で，その他の場合はすべて真となるような命題．この命題を「\(p\)ならば\(q\)」と呼び，\(p\rightarrow q\)と表す．

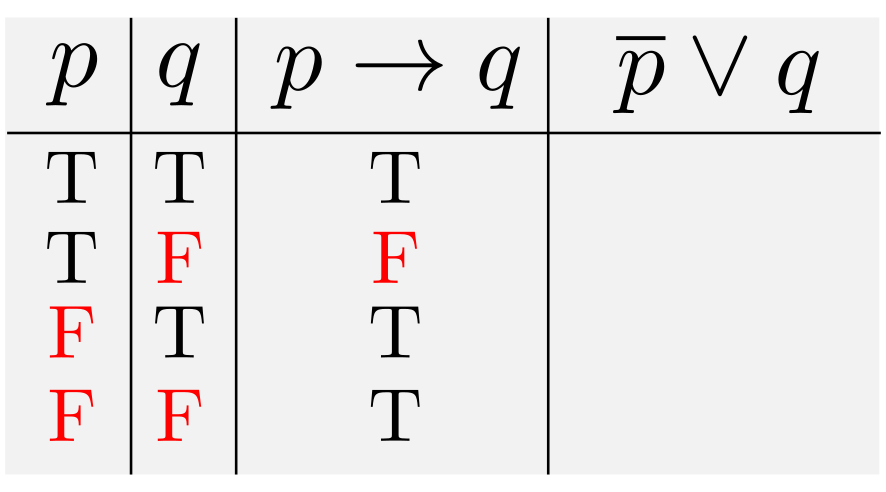
上が\(p\land q,~p \lor q,~\lnot p,~p\rightarrow q\)の定義です．…が，とても見にくいですね．そこで以下のような表でまとめてみます．Tは真(True)を，Fは偽(False)を表すとします．


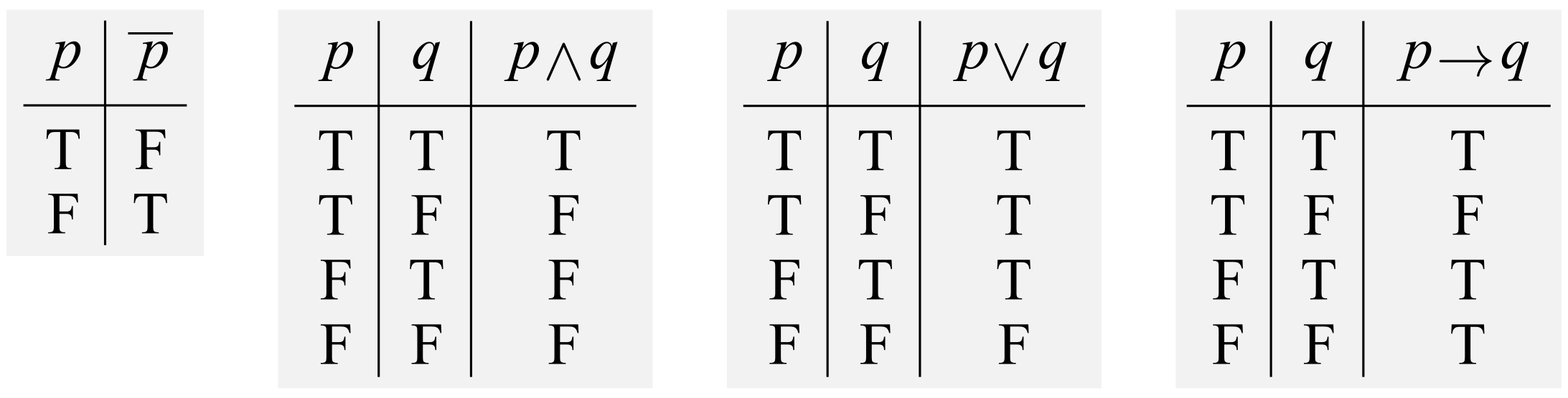
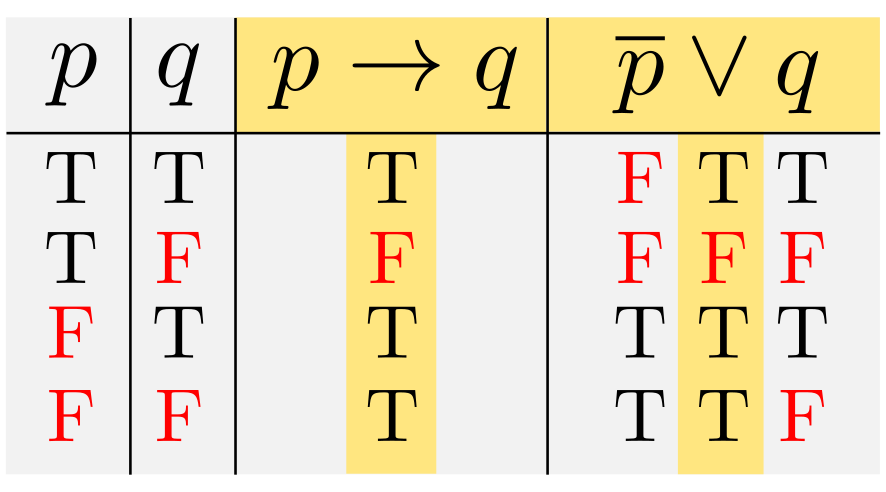
大分見やすくなりました．これを，「真理表（または真理値表）」と呼びます．以後，\(p\land q,~p \lor q,~\lnot p,~p\rightarrow q\)を上の表に従う命題とし，これらの表に基づき各種命題の真偽判定していくことになります．

（補足１）
ところで，この定義の中で唯一違和感があるとしたら，「『\(p\)ならば\(q\)』は，\(p\)が偽のとき\(q\)の真偽に関わらず真とする」という点かと思います．定義なんだからつべこべ言わず受け入れましょう，と言いたいところですが（「定義する」と言われたら受け入れるしかない？），あえて感覚的な説明をするとしたら，次のように考えると受け入れやすいかもしれません：

とある家庭で父親が息子に言いました「テストで満点をとったら，スマホを買ってあげるよ」と．

このとき，次の４つのケースが考えられます．

    1. 息子が満点をとり，父親がスマホを買ってあげる
    2. 息子が満点をとり，父親がスマホを買ってあげない
    3. 息子は満点をとれず，父親がスマホを買ってあげる
    4. 息子は満点をとれず，父親がスマホを買ってあげない

このうち，父親が「約束を守った・破った」ことになるのはどれかを考えてみます．１．これは父親はきちんと約束を守っています．２．これは父親は明らかに約束を破っていますね．さて，３と４についてはこのように考えられないでしょうか：

そもそも息子が満点を取ってない以上，父親が買ってあげようとも（満点とれなかったのにラッキーですね）買ってあげずとも，約束を破ったことにはならない，すなわち約束を守ったことになる．

このように考えると「ならば」を上のように定義することが感覚的に受け入れられるのではないでしょうか．

（補足２）
命題\[p \longrightarrow q\]
が真であることを，
\[p \Longrightarrow q\]
と表します．ですから，「\(p \Rightarrow q\)」は「\(p \rightarrow q\)が真である（成り立つ）」と読み替えられます．

© 2024 佐々木数学塾, All rights reserved.