(証明)
\[
\begin{align*}
P(B_i|A)&=\frac{P(B_i\cap A)}{P(A)}&\cdots~(1)\\
&=\frac{P(B_i)P(A|B_i)}{ \sum^{\infty}_{j=1}P(A\cap B_j)}&\cdots~(2)\\
&=\frac{P(B_i)P(A|B_i)}{ \sum^{\infty}_{j=1}P(A)P(B_j|A)}&\cdots~(3)
\end{align*}
\]
\((1)\)は条件付き確率の定義そのものです.\((2)\)の分子は確率の乗法定理より,分母は全確率の定理によります.\((2)\)の分母に再び確率の乗法定理を用いると\((3)\)となります.(証明終)
この「ベイズの定理」は,証明の過程を見て貰えば分かる通り,条件付き確率の定義式を確率の乗法定理と全確率の定理を用いて変形したものに過ぎません.なので,この式は「根っこはあくまで条件付き確率の定義式だ」という認識のもと,あとは(その条件付き確率の定義式を)問題に応じて便宜変形する,というような使い方をすればよいと思います(つまり「条件付き確率」の定義を納得しており,「確率の乗法定理」と「全確率の定理」を知ってさえいればベイズの定理そのものを覚える必要はない,ということ).
このベイズの定理を用いて,次の問題を解いてみます.早稲田大の問題です.
(早稲田・文)
「抜き出された1枚がダイヤ」という事象を\(A\),「3枚ともダイヤ」という事象を\(B\)とおきます.すると,求める確率は\(P(A|B)\)と表せます.これをベイズの定理を用いて計算してみましょう.
\[
\begin{align*}
P(A|B)&=\frac{P(A\cap B)}{P(B)}\\
&=\frac{P(A)P(B|A)}{P(B\cap A)+P(B\cap \overline{A})}\\
&=\frac{P(A)P(B|A)}{P(A\cap B)+P(\overline{A}\cap B)}\\
&=\frac{P(A)P(B|A)}{P(A)P(B|A)+P(\overline{A})P(B|\overline{A})}\\
&=\frac{\frac{{}_{13} \mathrm{C}_1}{{}_{54} \mathrm{C}_1}\times \frac{{}_{12} \mathrm{C}_3}{{}_{53} \mathrm{C}_3}}{\frac{{}_{13} \mathrm{C}_1}{{}_{54} \mathrm{C}_1}\times \frac{{}_{12} \mathrm{C}_3}{{}_{53} \mathrm{C}_3}+\frac{{}_{39} \mathrm{C}_1}{{}_{54} \mathrm{C}_1}\times \frac{{}_{13} \mathrm{C}_3}{{}_{53} \mathrm{C}_3}}\\
&=\frac{10}{49}
\end{align*}
\]
となります.


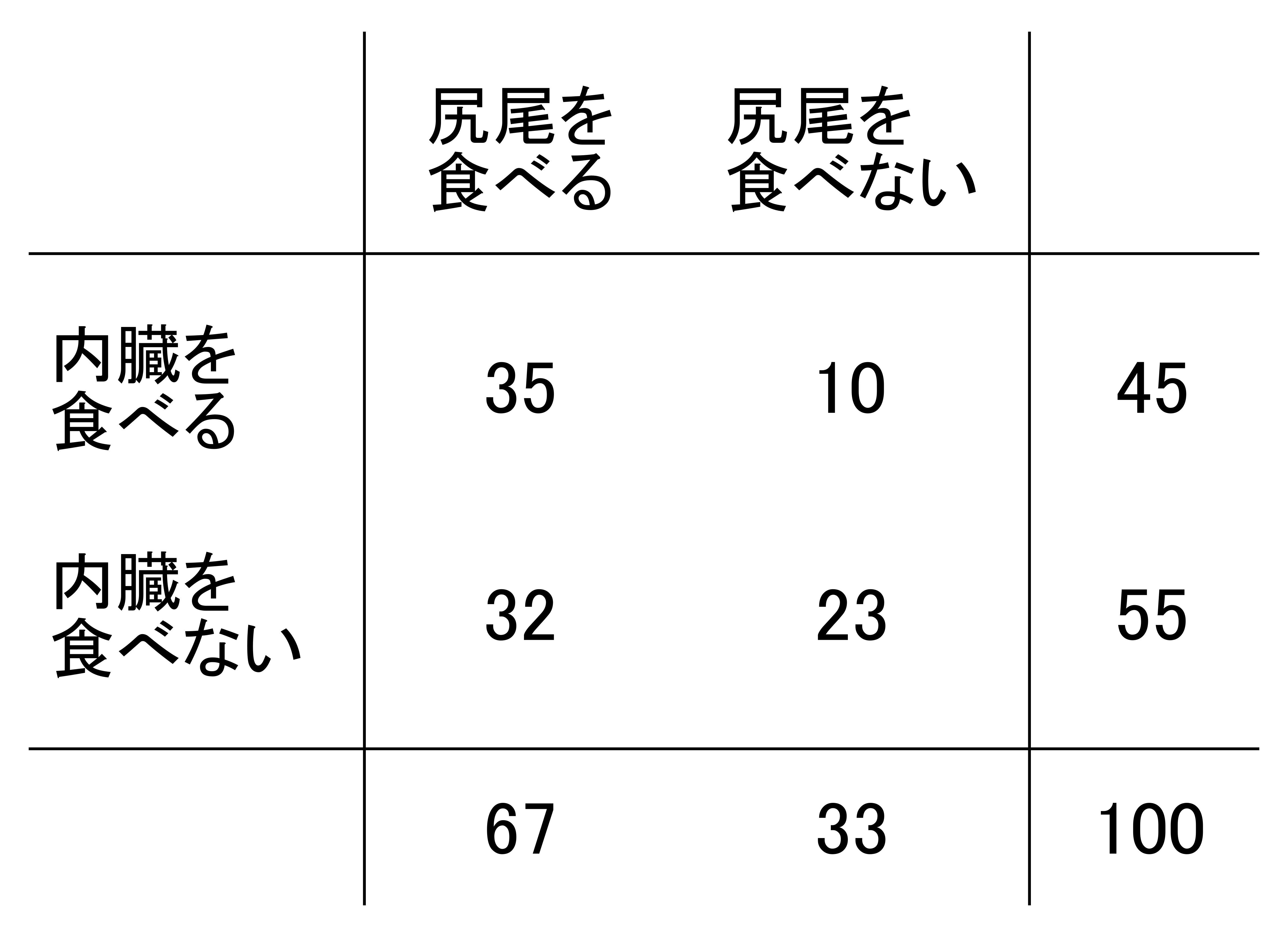 問題
問題