前回のプレゼント交換会を次の表で考えます.例えば前回の例
\[
\left(
\begin{array}{ccc}
1 & 2 & 3 & 4 & 5\\
2 & 1 & 4 & 5 & 3
\end{array}
\right)
\]であれば
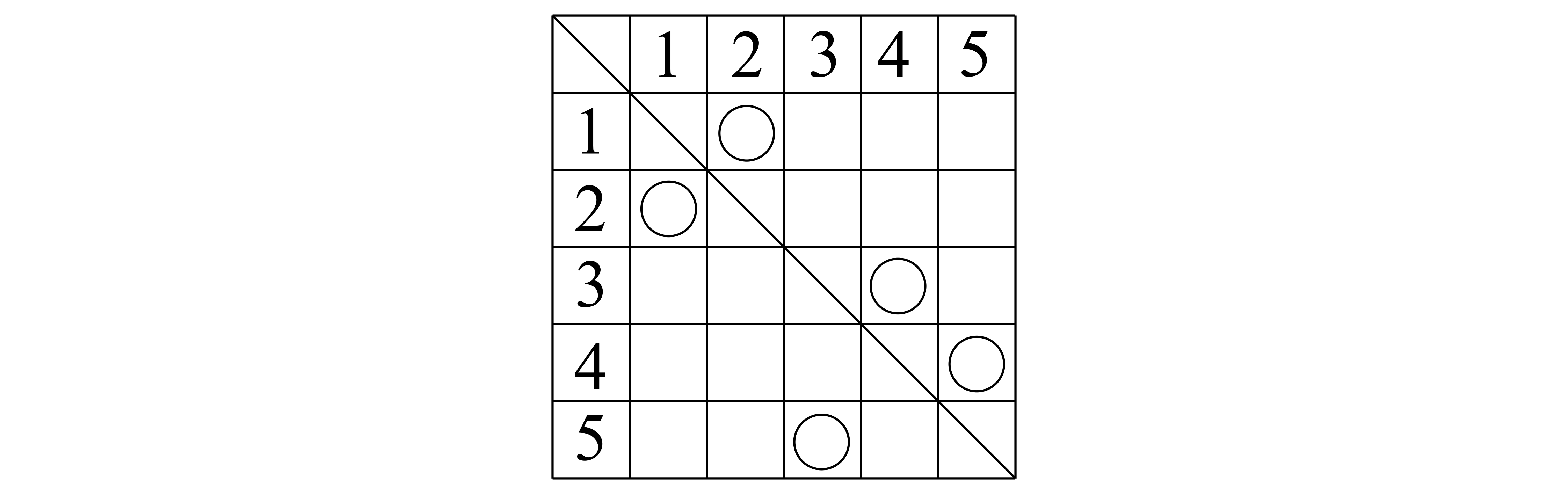
と表し,
\[
\left(
\begin{array}{ccc}
1 & 2 & 3 & 4 & 5\\
2 & 3 & 4 & 5 & 1
\end{array}
\right)
\]であれば
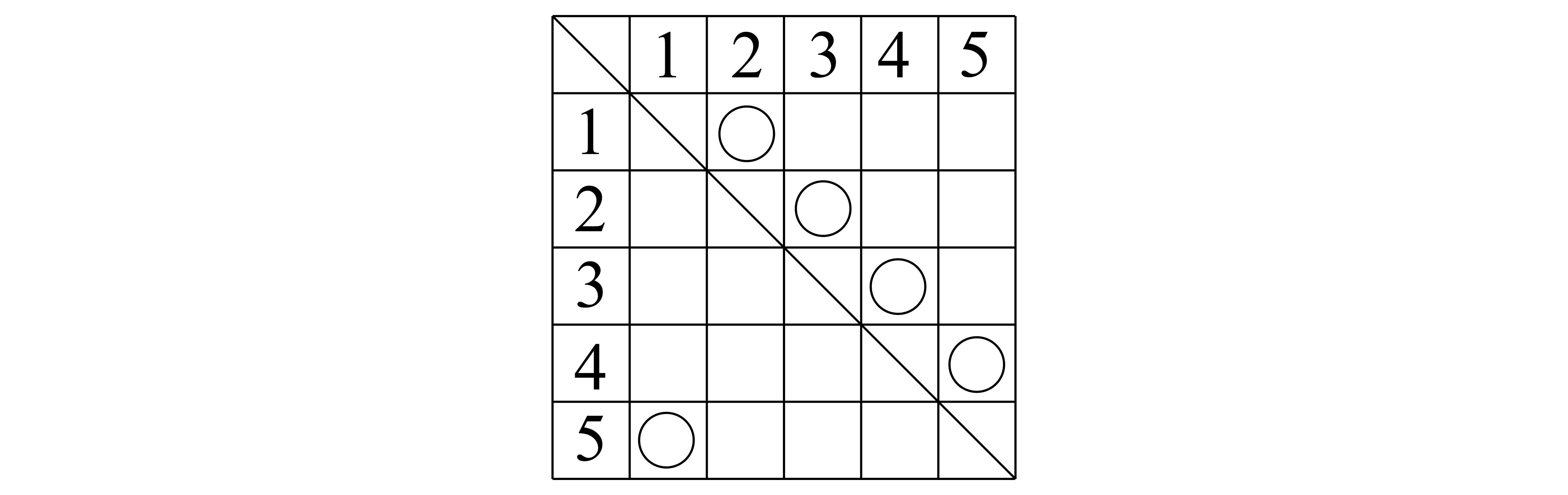
といった具合です.
以下,\(n\)個の完全順列の総数を\(f(n)\)で表すことにします(なので求めたいものは\(f(5)\)).また,\(i\)行\(j\)列にある欄を\((i,~j)\)と表すことにします.
ここで,まず1行目に着目します.1行目で〇が入り得るのは,2,3,4,5のいずれかです.
ここでは\((1,~2)\)に〇が入る場合を考えてみます.
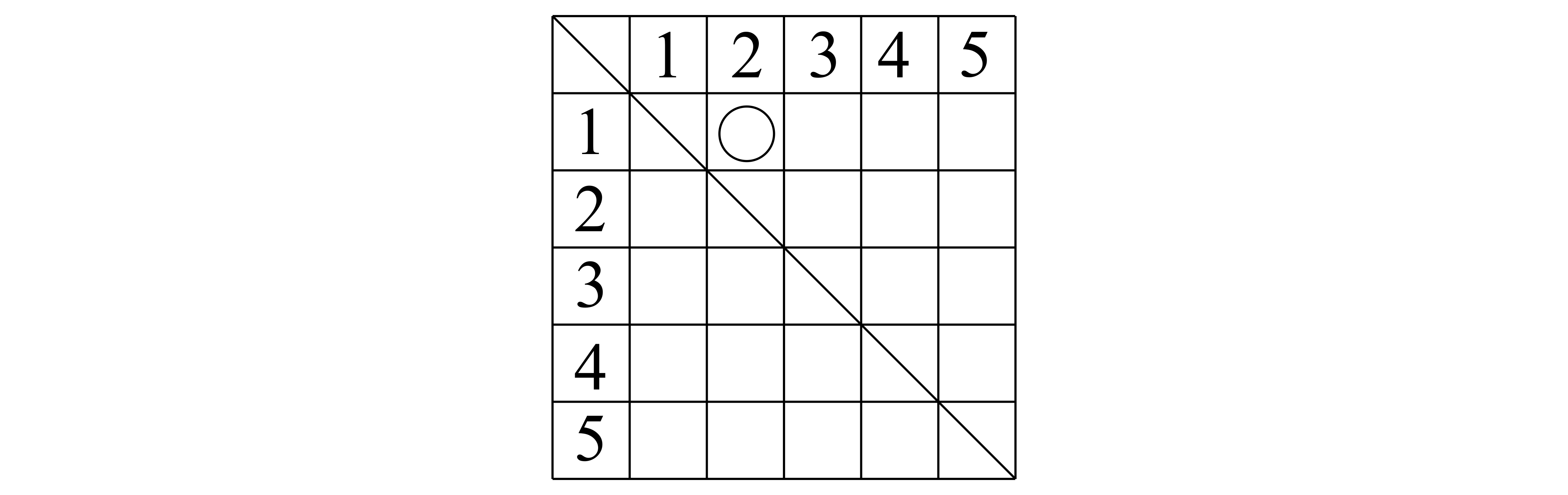
こんな場合です.
次に,2行目に着目します.ここでは,
(ⅰ)\((2,~1)\)に〇が入る場合
と,
(ⅱ)\((2,~1)\)に入らない場合(\((2,~3)\)か\((2,~4)\)か\((2,~5)\)に入る場合)
が考えられますので,場合分けしてみます.表で表すと,
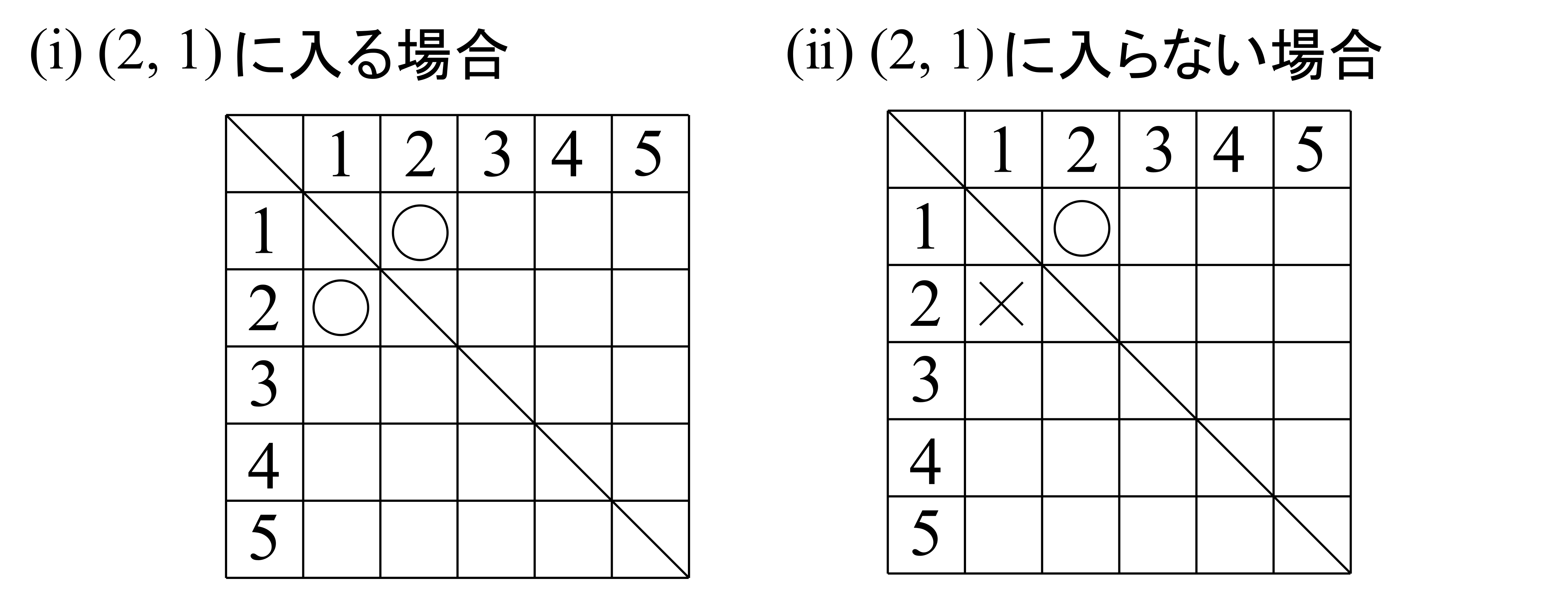
という具合です.
まず(ⅰ)の場合について考察してみます.
この場合,下図の黄色と緑のライン上に〇が来ることはありません(〇が同じ行または列でダブるとそれはプレゼントを2つ受け取るor与えることを意味してしまうから).なので,どうせ〇が来ないのならいっそのこと消しゴムで消して繋げてしまいましょう.
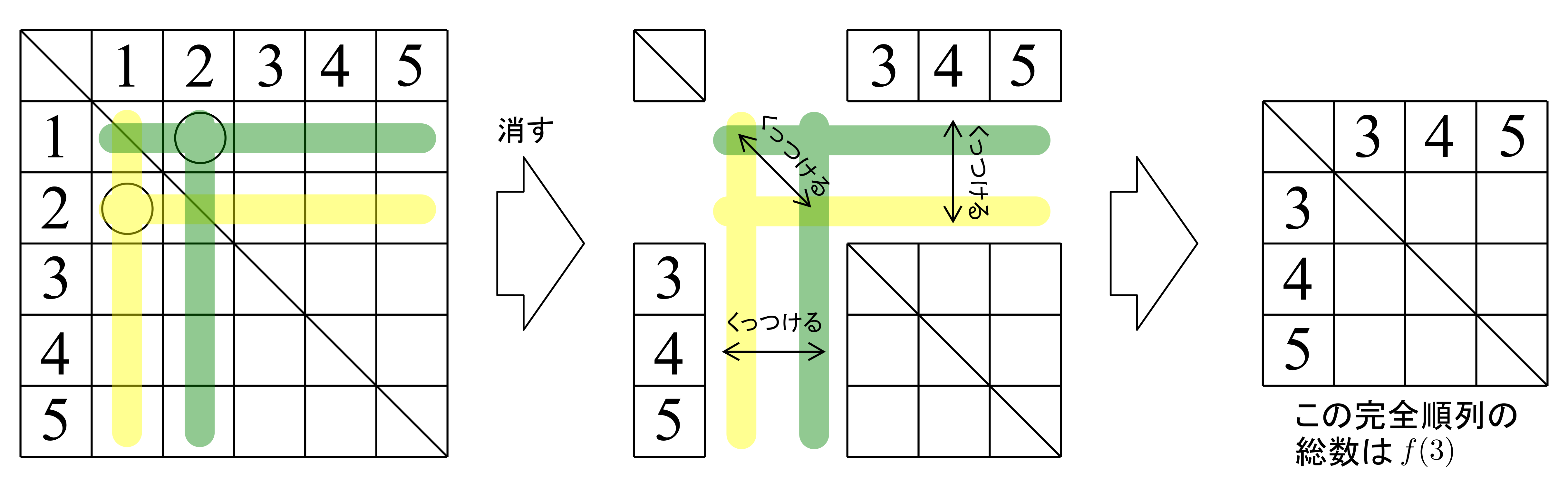
そうして出来上がった表を眺めると,この完全順列の総数は\(f(3)\)となることがわかります.これで(ⅰ)のときすなわち\((2,~1)\)に〇が入る場合その完全順列の総数は\(f(3)\)であることが分かりました.
次に(ⅱ)の場合について考えてみます.(ⅰ)のときと同様に考え,
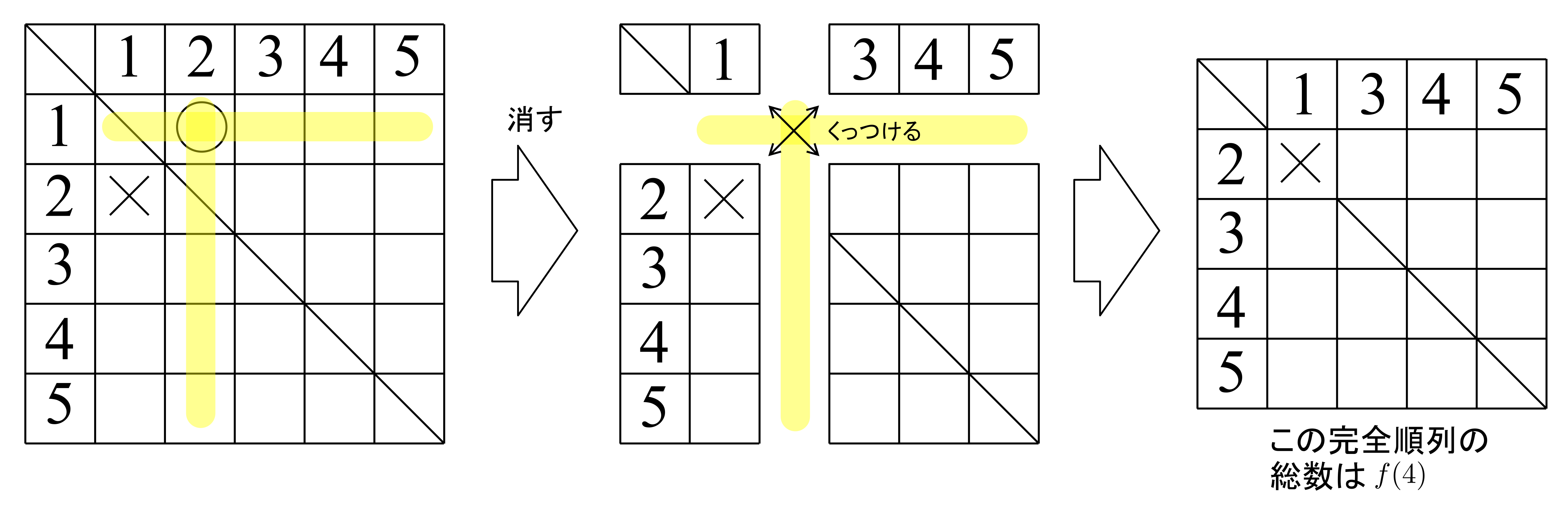
出来上がった表を眺めると,この完全順列の総数は\(f(4)\)となることがわかります.これで(ⅱ)のとき\((2,~1)\)に〇が入らない場合その完全順列の総数は\(f(4)\)であることが分かりました.
ここまででしたことをまとめます.
最初の場合分けで4通り,この4通りそれぞれにおいて,(ⅰ)タイプと(ⅱ)タイプに分類したので,結局,求める\(f(5)\)は,
\[f(5)=4(f(3)+f(4))\]
となります.
以上の議論を\(5\)人のプレゼント交換会ではなく,\(n\)人で置き換えると,
\[f(n+2)=(n+1)(f(n)+f(n+1))\]という漸化式が得られます.これを利用すれば,
\[
\begin{align*}
&f(3)=2(f(1)+f(2))\\
&f(4)=3(f(2)+f(3))\\
&f(5)=4(f(3)+f(4))\\
\end{align*}
\]
\(f(1)=0,~f(2)=1\)ですから,順次計算することで
\(f(3)=2,~f(4)=9,~f(5)=44\)となり答えを得ます.
このように考えると,プレゼント交換会の人数がそれなりに多くても,漸化式\(f(n+2)=(n+1)(f(n)+f(n+1))\)を考えることで単純な計算により完全順列の総数を算出できることが分かります.
次は,完全順列の総数の一般化を考えてみます.

