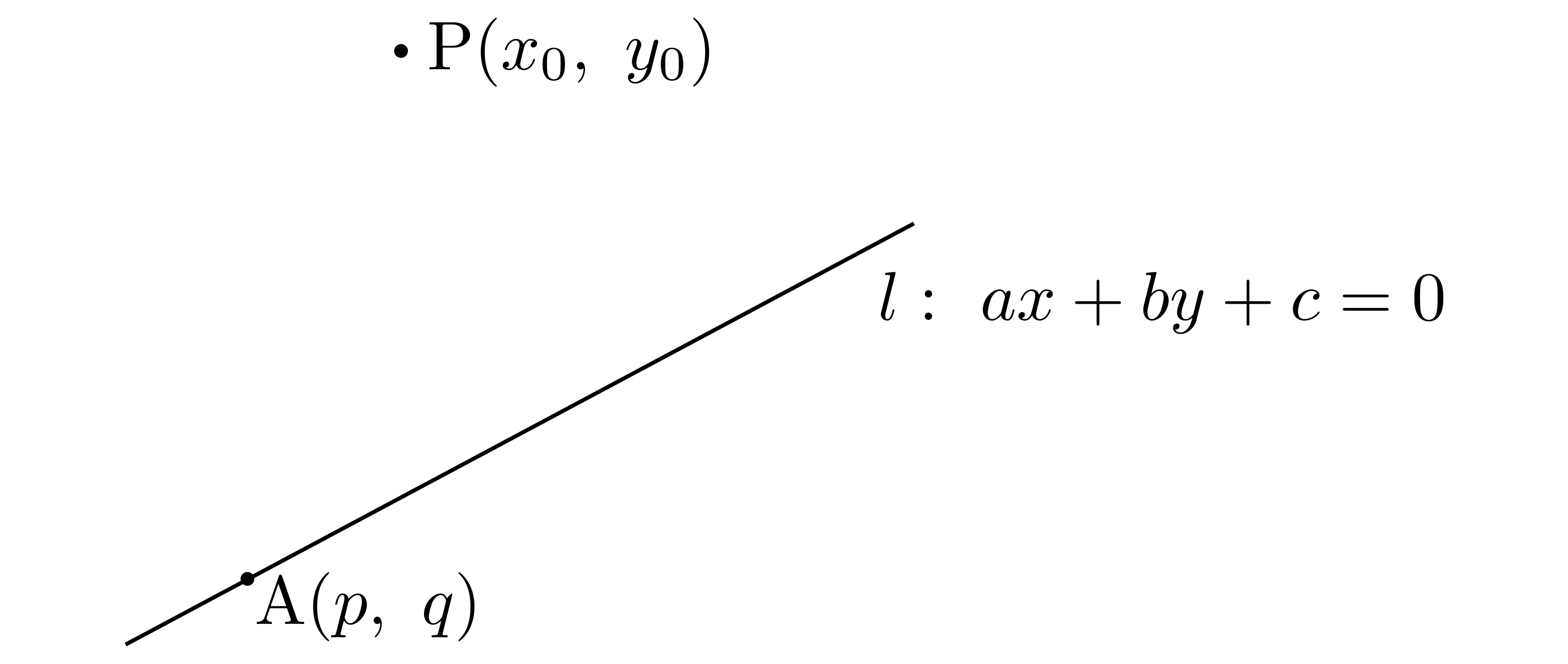位置ベクトルとは,「始点が原点であるようなベクトル」のことです.
平面上の任意の点\(\mathrm{A}\)に対して,ベクトル\(\overrightarrow{\mathrm{OA}}=\boldsymbol{a}\)をその位置ベクトルという.ただし\(\mathrm{O}\)は座標の原点である.
松坂和夫「線形代数入門」岩波書店
なぜ「始点が原点である」だけで「位置ベクトル」なんて名前をつけてまで差別化するのでしょうか.それは,始点が原点にあるがゆえに,ベクトルの成分とベクトルの先っぽ(終点)が指し示す点の座標が一致するからです.例えば,点\(\mathrm{P}\)の座標が\((2,1)\)であるならば,位置ベクトル\(\overrightarrow{\mathrm{OP}}\)の成分は\(\left(\begin{array}{c} 2 \\ 1 \\ \end{array} \right)\)だし,逆に位置ベクトル\(\overrightarrow{\mathrm{OP}}\)の成分が\(\left(\begin{array}{c} 2 \\ 1 \\ \end{array} \right)\)ならば点\(\mathrm{P}\)の座標は\((2,1)\)です.単純なことですが,位置ベクトルにおいてはこの性質-座標とベクトルが同一視できること-が極めて重要です.

※注意1 ベクトルの成分を縦に書いたものを「列ベクトル(または縦ベクトル)」と呼びます.他方,ベクトルの成分を横に書いたものを(高校教科書での記法)「行ベクトル(横ベクトル)」とよびます.どちらも同じものですがベクトルの成分を書くときは高校段階であっても行ベクトルではなく列ベクトルで表記した方がいいでしょう.どうせ大学へ行けば列ベクトル表記の方がむしろ当たり前になりますし,高校段階であってもそれが「成分」なのか「座標」なのかを意識するためにベクトル(の成分)は横,座標は縦,と区別して書くべきです.また列ベクトルだと成分計算がし易いという利点もあります.テスト・模試等でも列ベクトルを用いても大丈夫です.減点されることは絶対にありえませんから.
※注意2 問題によっては「点\(A\)に関する位置ベクトルを…」といい,始点を\(A\)などととることがあります.その場合には,「点\(A\)を自前で設定した座標系の原点」と考えればいいだけです.
位置ベクトルをこのように「始点を原点にとったときのベクトル;矢印の終点が指し示す座標」と見なせば,次のような問題も容易に発想できます.
半径の円\(a\)の円が\(x\)軸上を滑ることなく回転するとき,円上の定点\(\mathrm{P}\)の描くサイクロイドの媒介変数表示を求めよ.ただし,点\(\mathrm{P}\)の最初の位置を原点\(\mathrm{O}\),円の中心の最初の位置を\((0,a)\)とする.
どのような状況なのかイメージするは,言葉で説明するより図を見た方が早いでしょう.
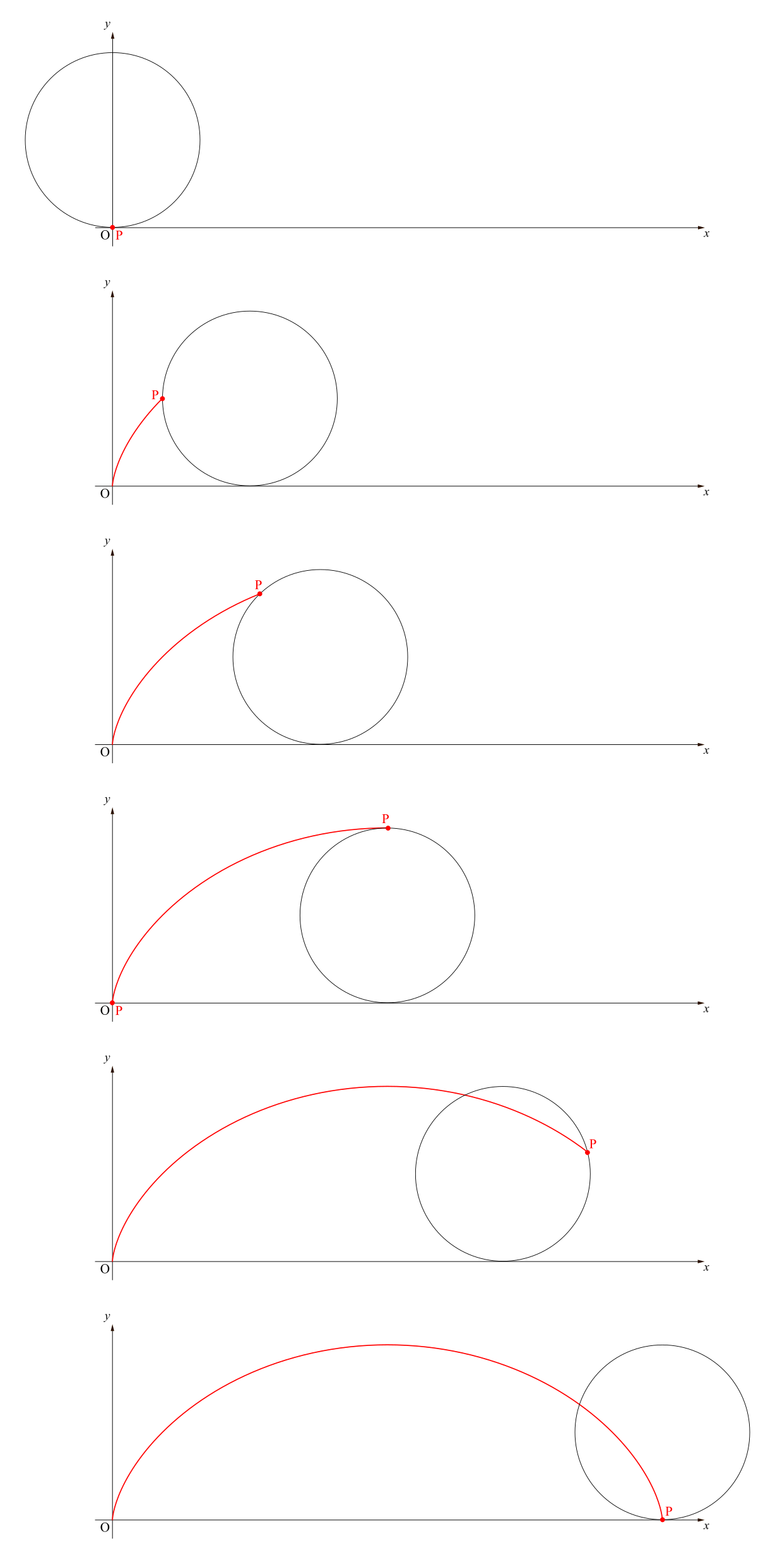
この赤線上の点\(\mathrm{P}\)の座標を求めることを考えます.欲しいものは点\(\mathrm{P}\)の座標なわけですが,『点\(\mathrm{P}\)の座標=\(\overrightarrow{\mathrm{OP}}\)の成分』でしたから,位置ベクトル\(\overrightarrow{\mathrm{OP}}\)を求めることにします.
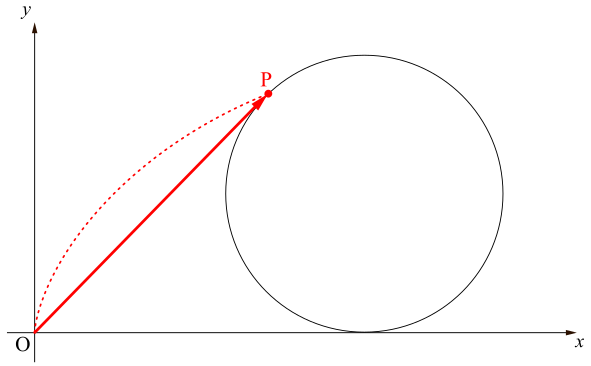
ベクトルなのだから,ベクトルの和の定義により,下図のように\[\overrightarrow{\mathrm{OP}}=\overrightarrow{\mathrm{OH}}+\overrightarrow{\mathrm{HC}}+\overrightarrow{\mathrm{CP}}\]と分解できます.
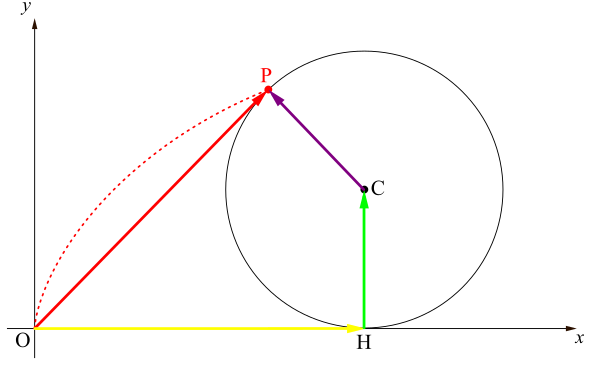
したがって\(\overrightarrow{\mathrm{OH}},~\overrightarrow{\mathrm{HC}},~\overrightarrow{\mathrm{CP}}\)をそれぞれ求めればよい.
まず\(\overrightarrow{\mathrm{OH}}\)から.
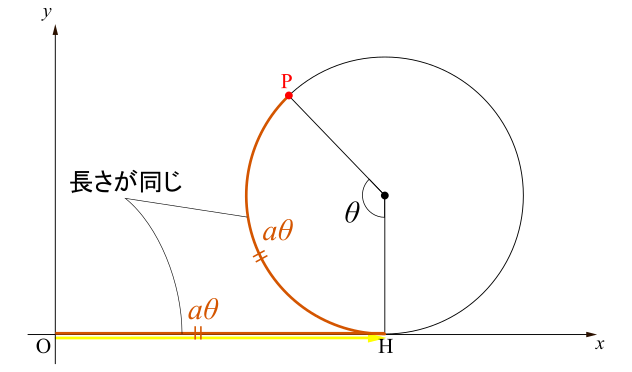 このベクトルは始点が既に原点にありますから,位置ベクトル,すなわちその成分と終点が指し示す座標が一致しているはずです.したがって\(\overrightarrow{\mathrm{OH}}\)の終点が指し示す座標を調べればよい.\(\mathrm{OH}=\text{孤}\mathrm{PH}\)であることに注意すると(「滑らずに」転がしたんだから!右図参照),\(\mathrm{OH}=a\theta\).したがって点\(\mathrm{H}\)の座標は\((a\theta,0)\)で,(座標と成分が対応するから)\(\overrightarrow{\mathrm{OH}}\)の成分は\(\left(\begin{array}{c} a\theta \\ 0 \\ \end{array} \right)\)となります.
このベクトルは始点が既に原点にありますから,位置ベクトル,すなわちその成分と終点が指し示す座標が一致しているはずです.したがって\(\overrightarrow{\mathrm{OH}}\)の終点が指し示す座標を調べればよい.\(\mathrm{OH}=\text{孤}\mathrm{PH}\)であることに注意すると(「滑らずに」転がしたんだから!右図参照),\(\mathrm{OH}=a\theta\).したがって点\(\mathrm{H}\)の座標は\((a\theta,0)\)で,(座標と成分が対応するから)\(\overrightarrow{\mathrm{OH}}\)の成分は\(\left(\begin{array}{c} a\theta \\ 0 \\ \end{array} \right)\)となります.
次に\(\overrightarrow{\mathrm{HC}}\).
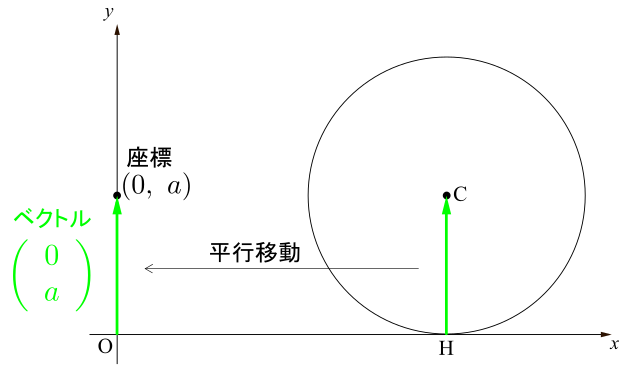 始点が原点にあれば,そのまま終点が指し示す座標を読めばいいのですが,これは始点は原点ではありませんね.しかしベクトルは向きと大きささえ変えさえしなければ自由に動かせるのでしたから,始点を原点にとってから,その終点の座標を読めばよいでしょう.始点を原点にとったときのベクトルの終点が指し示す座標は\((0,~a)\)ですから,そのベクトルの成分は\(\overrightarrow{\mathrm{OH}}\)の成分は\(\left(\begin{array}{c} 0 \\ a \\ \end{array} \right)\)となります.
始点が原点にあれば,そのまま終点が指し示す座標を読めばいいのですが,これは始点は原点ではありませんね.しかしベクトルは向きと大きささえ変えさえしなければ自由に動かせるのでしたから,始点を原点にとってから,その終点の座標を読めばよいでしょう.始点を原点にとったときのベクトルの終点が指し示す座標は\((0,~a)\)ですから,そのベクトルの成分は\(\overrightarrow{\mathrm{OH}}\)の成分は\(\left(\begin{array}{c} 0 \\ a \\ \end{array} \right)\)となります.
最後に\(\overrightarrow{\mathrm{CP}}\).
やはり始点を原点にとってから,その終点の座標を読みましょう.始点を原点にとったときのベクトルの終点が指し示す座標は
\begin{align*}
&(a\cos\left(-\left(\frac{\pi}{2}+\theta\right)\right),~a\sin\left(-\left(\frac{\pi}{2}+\theta\right)\right))\\
=&(a\cos\left(\frac{\pi}{2}+\theta\right),~-a\sin\left(\frac{\pi}{2}+\theta\right))\\
=&(-a\sin \theta,~-a \cos \theta)
\end{align*}
ですから,求めるベクトルの成分は\(\left(\begin{array}{c} -a\sin \theta \\ -a \cos \theta \\ \end{array} \right)\)となります.

以上により,
\begin{align*}
\overrightarrow{\mathrm{OP}}&=\overrightarrow{\mathrm{OH}}+\overrightarrow{\mathrm{HC}}+\overrightarrow{\mathrm{CP}}\\
&=\left(\begin{array}{c} a\theta \\ 0 \\ \end{array} \right)+\left(\begin{array}{c} 0 \\ a \\ \end{array} \right)+\left(\begin{array}{c} -a\sin \theta \\ -a \cos \theta \\ \end{array} \right)\\
&=\left(\begin{array}{c} a(\theta-\sin \theta) \\ a(1 – \cos \theta) \\ \end{array} \right)\\
\end{align*}
(くどいようですが)位置ベクトルの成分とその終点が指し示す座標は対応しているのですから,結局,
\[
\begin{eqnarray}
\begin{cases}
x = a(\theta-\sin \theta) & \\
y = a(1 – \cos \theta) &
\end{cases}
\end{eqnarray}
\]
が得られたことになります.
位置ベクトルについて強調すべきはその定義「始点が原点であるようなベクトル」であり,ゆえに,「ベクトルを座標と見なせる」点だと思うのですが,教科書はそこが強調されていない.僕はかつて予備校でこれを習いましたが,ベクトルが初めて「道具として役に立つ」と感じられたこと,そしてベクトルを座標とみなすという別の概念を同一視するという感覚が新鮮で嬉しかった記憶があります.実際,位置ベクトルを用いるとカージオイドやエピサイクロイドなどの他の曲線もまったく同様に媒介変数表示できますし,また数学Ⅲで学ぶ複素数平面においても有用です(例によって教科書では位置ベクトルを用いた説明などしてはくれません).教科書を機械的・天下り的になぞるのもひとつの学習法ではありますが,こういったことを学ぶのもまた大事です.
ついでながら.教科書は「誤り・誤植がほとんどない」という意味においては最も信頼できる本のひとつだと思います.が,しかし,「誤りがないこと=最善」であるとは限りません.教科書と違う考え方・解法というものに抵抗を感じる人も少なくないと思いますが,食わず嫌いせずに興味をもって身に付けてみましょう.きっともう一皮むけますから.
もっと積極的に使おうぜ,位置ベクトル.
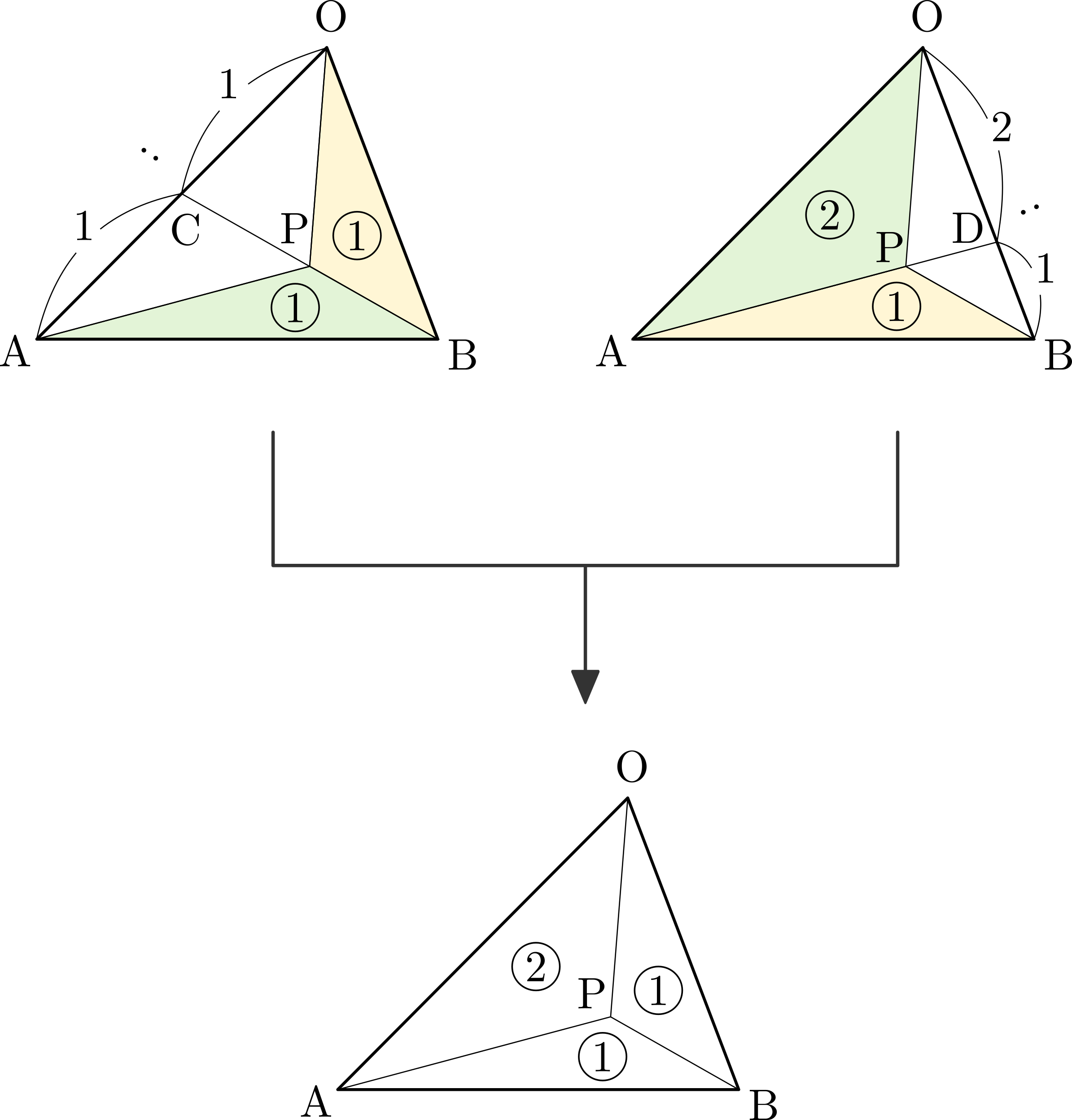
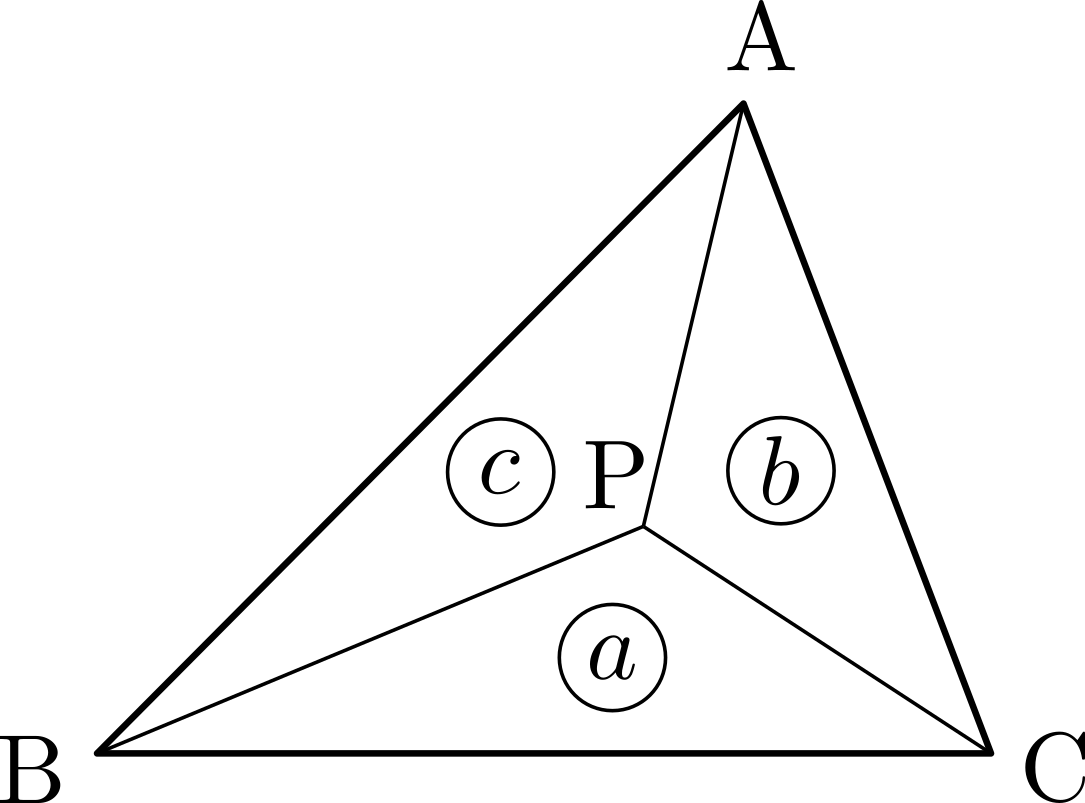 \(\triangle{\mathrm{ABC}}\)において,\(\triangle{\mathrm{PBC}}:\triangle{\mathrm{PCA}}:\triangle{\mathrm{PAB}}=a:b:c~\)のとき,\[\overrightarrow{\mathrm{AP}}=\frac{1}{a+b+c}(b\overrightarrow{\mathrm{AB}}+c\overrightarrow{\mathrm{AC}})\]
\(\triangle{\mathrm{ABC}}\)において,\(\triangle{\mathrm{PBC}}:\triangle{\mathrm{PCA}}:\triangle{\mathrm{PAB}}=a:b:c~\)のとき,\[\overrightarrow{\mathrm{AP}}=\frac{1}{a+b+c}(b\overrightarrow{\mathrm{AB}}+c\overrightarrow{\mathrm{AC}})\]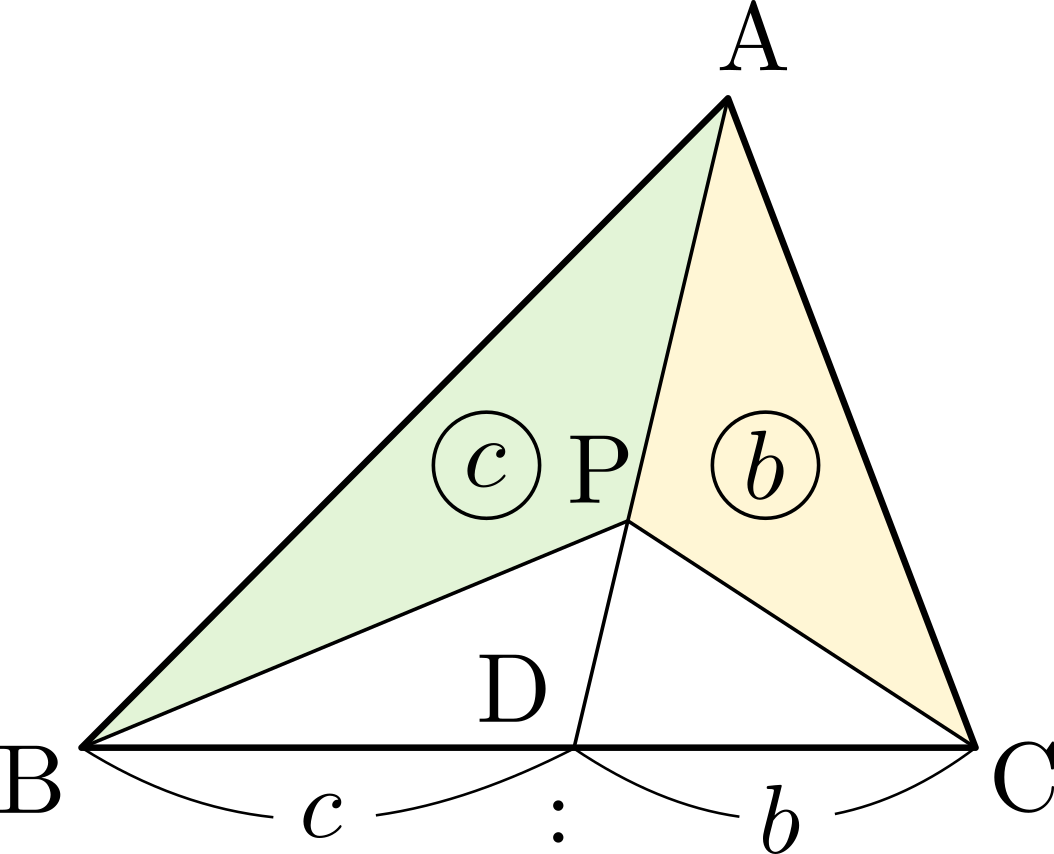 直線\(\mathrm{AP}\)と辺\(\mathrm{BC}\)との交点を\(\mathrm{D}\)とおくと,\(\triangle{\mathrm{PCA}}:\triangle{\mathrm{PAB}}=b:c\)より\(\mathrm{BD}:\mathrm{DC}=c:b\)であるから,内分の公式により\[\overrightarrow{\mathrm{AD}}=\frac{b\overrightarrow{\mathrm{AB}}+c\overrightarrow{\mathrm{AC}}}{c+b}\]
直線\(\mathrm{AP}\)と辺\(\mathrm{BC}\)との交点を\(\mathrm{D}\)とおくと,\(\triangle{\mathrm{PCA}}:\triangle{\mathrm{PAB}}=b:c\)より\(\mathrm{BD}:\mathrm{DC}=c:b\)であるから,内分の公式により\[\overrightarrow{\mathrm{AD}}=\frac{b\overrightarrow{\mathrm{AB}}+c\overrightarrow{\mathrm{AC}}}{c+b}\]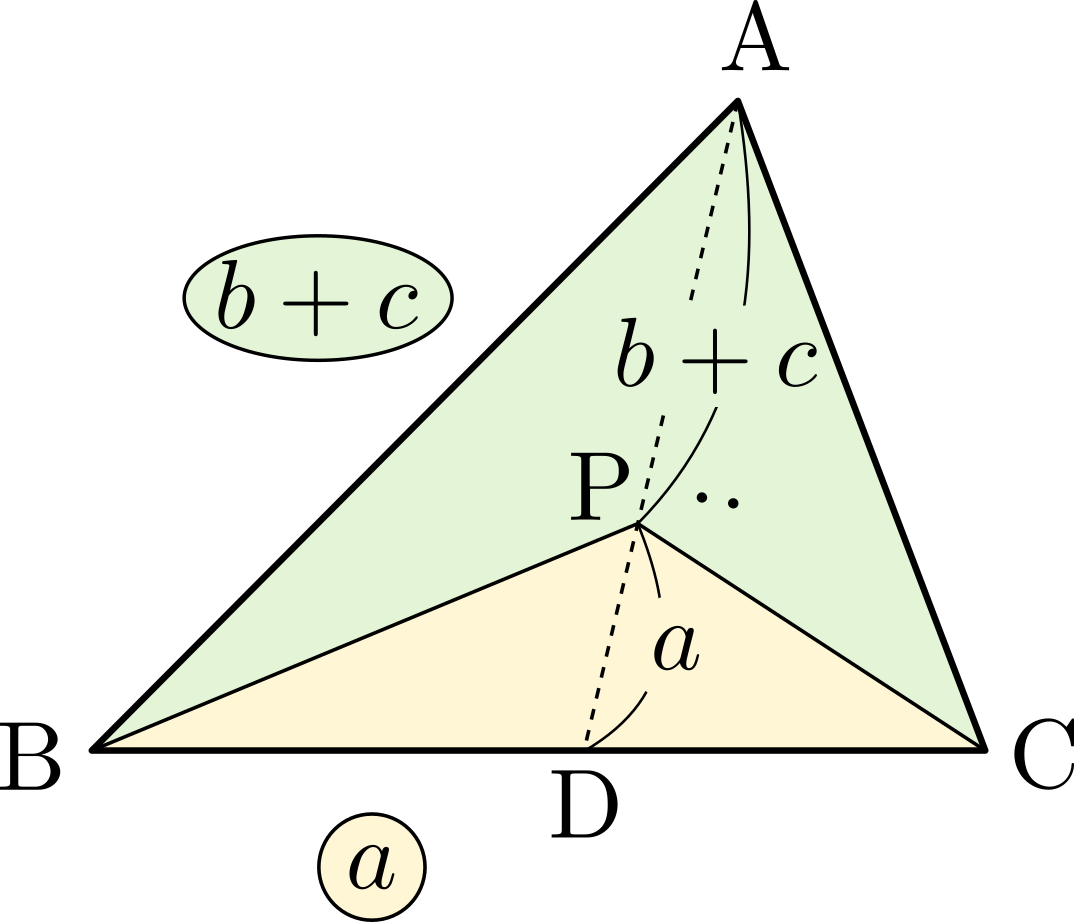 また,凹四角形\(\mathrm{ABPC}\)と\(\triangle{\mathrm{PBC}}\)の面積比が\(b+c:a\)であることから\(\mathrm{AP}:\mathrm{PD}=b+c:a\)だから\[\overrightarrow{\mathrm{AP}}=\frac{b+c}{a+b+c}\overrightarrow{\mathrm{AD}}\]
また,凹四角形\(\mathrm{ABPC}\)と\(\triangle{\mathrm{PBC}}\)の面積比が\(b+c:a\)であることから\(\mathrm{AP}:\mathrm{PD}=b+c:a\)だから\[\overrightarrow{\mathrm{AP}}=\frac{b+c}{a+b+c}\overrightarrow{\mathrm{AD}}\]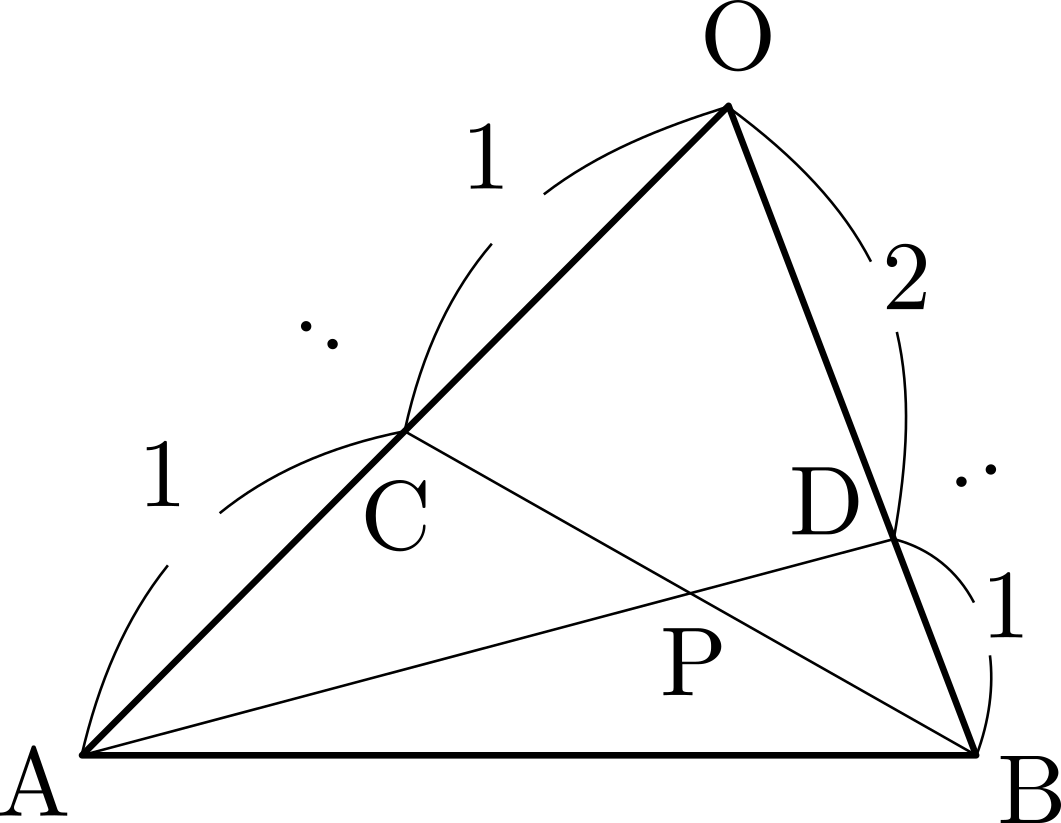


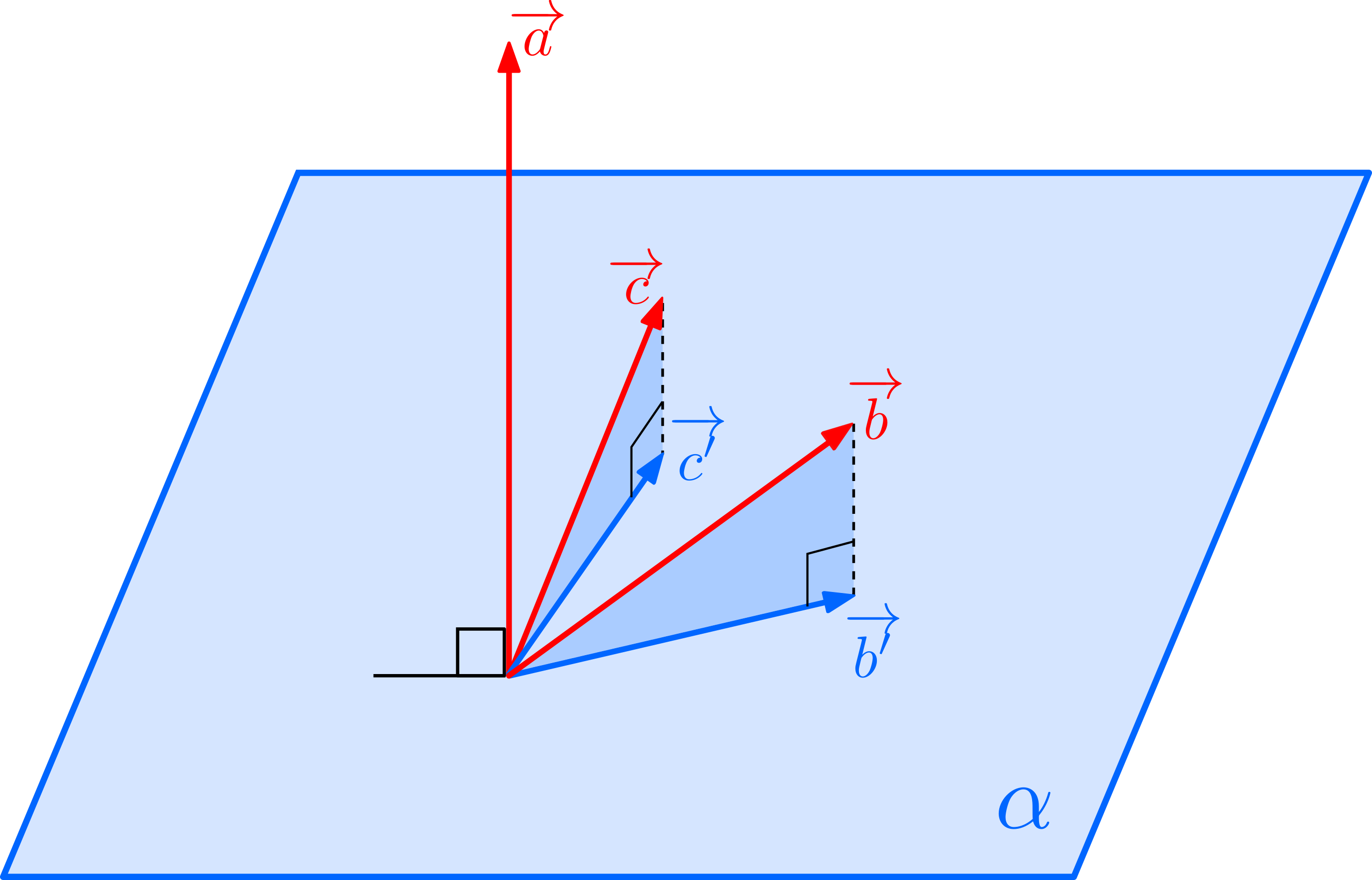
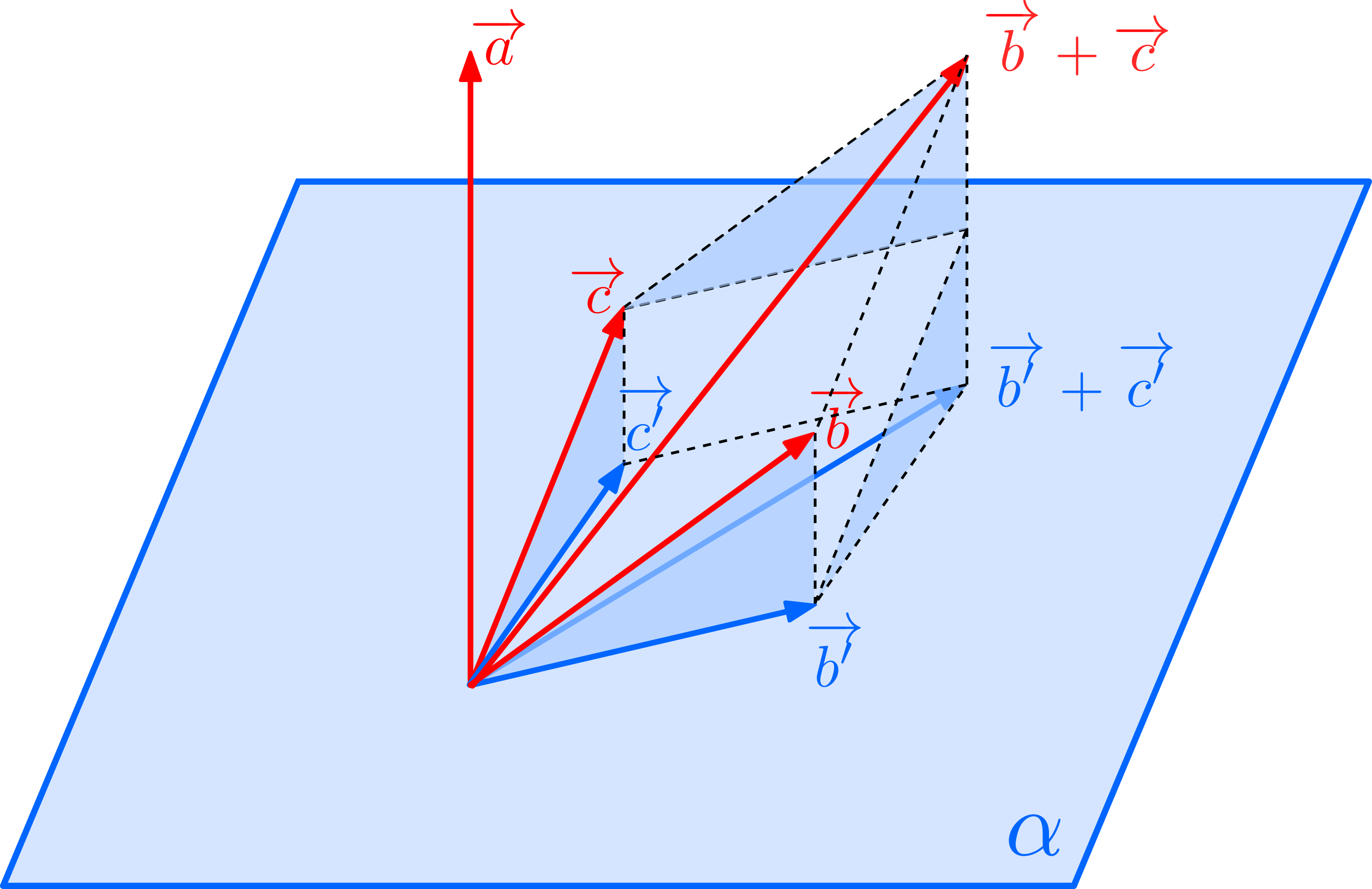
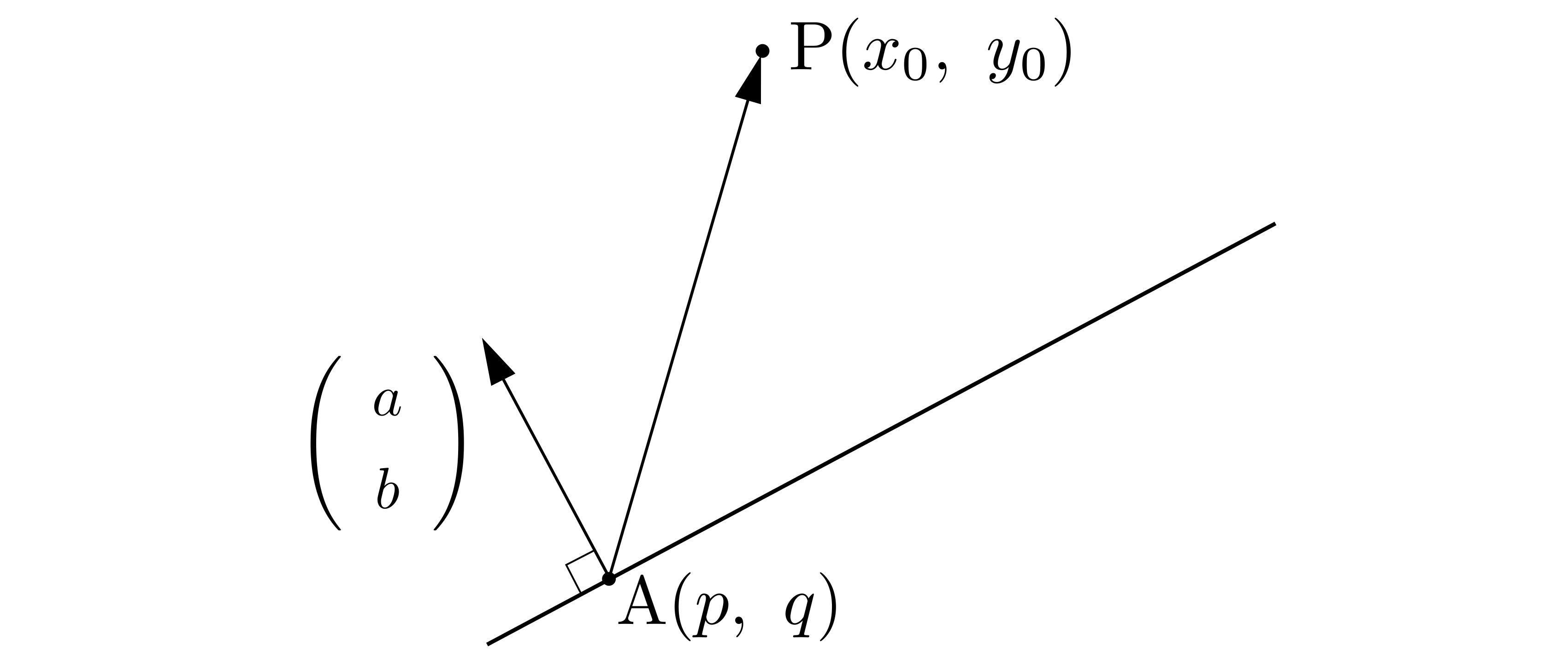
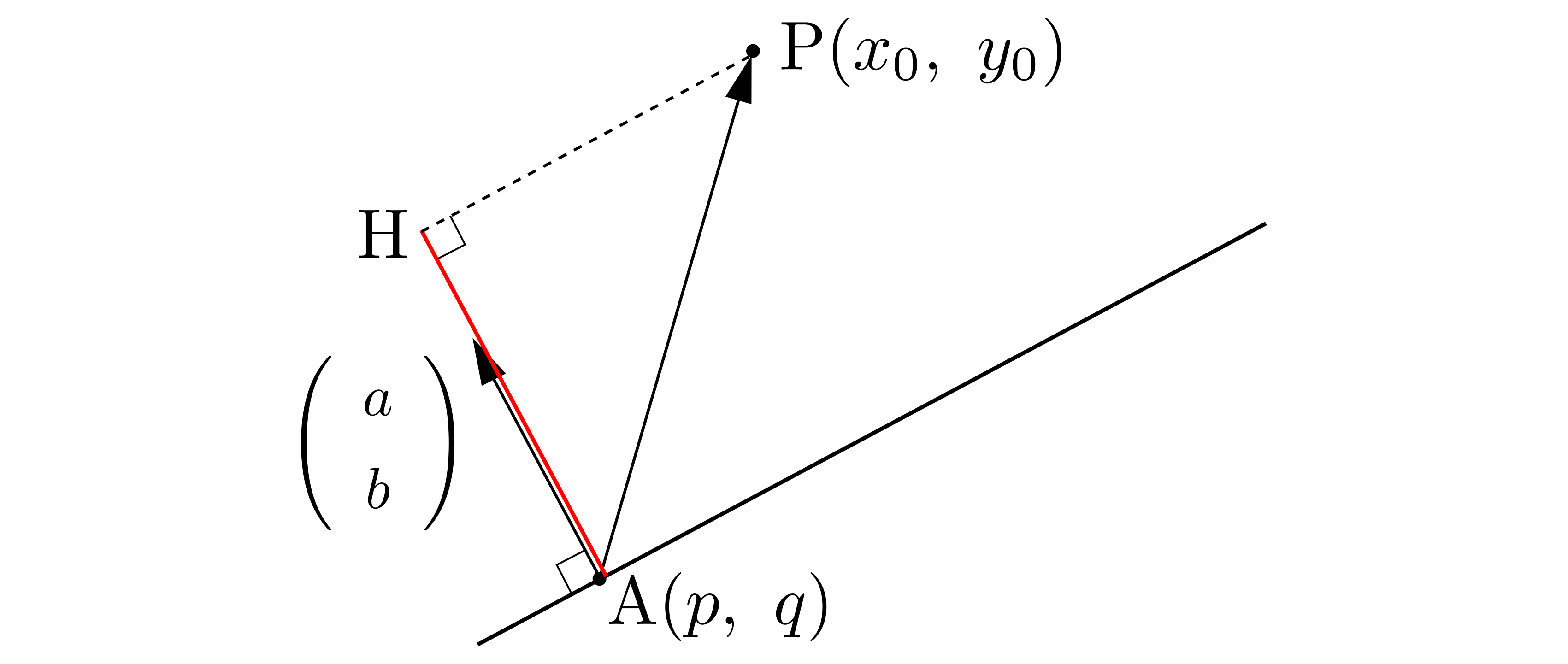
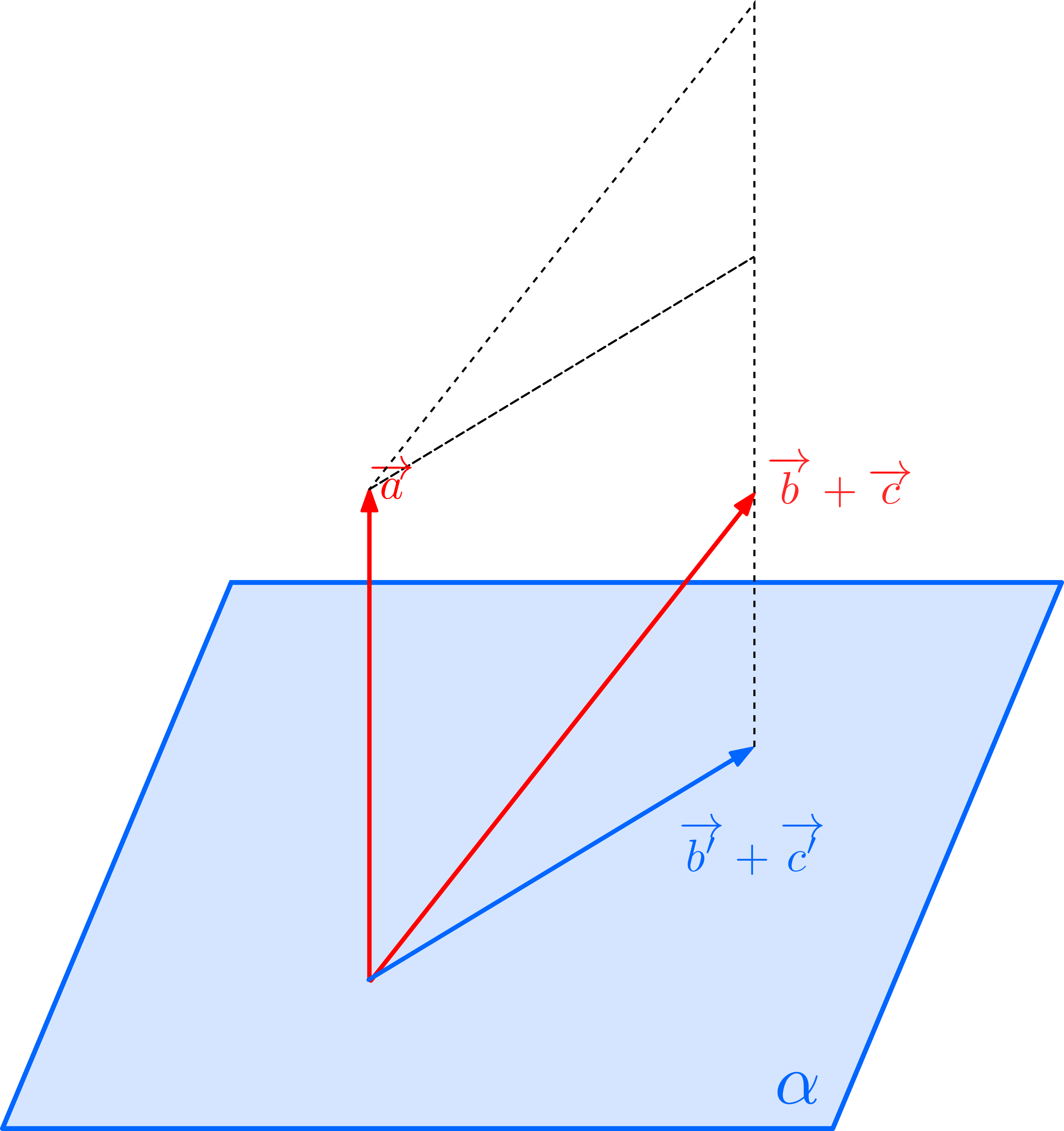 \((1)\)について:
\((1)\)について: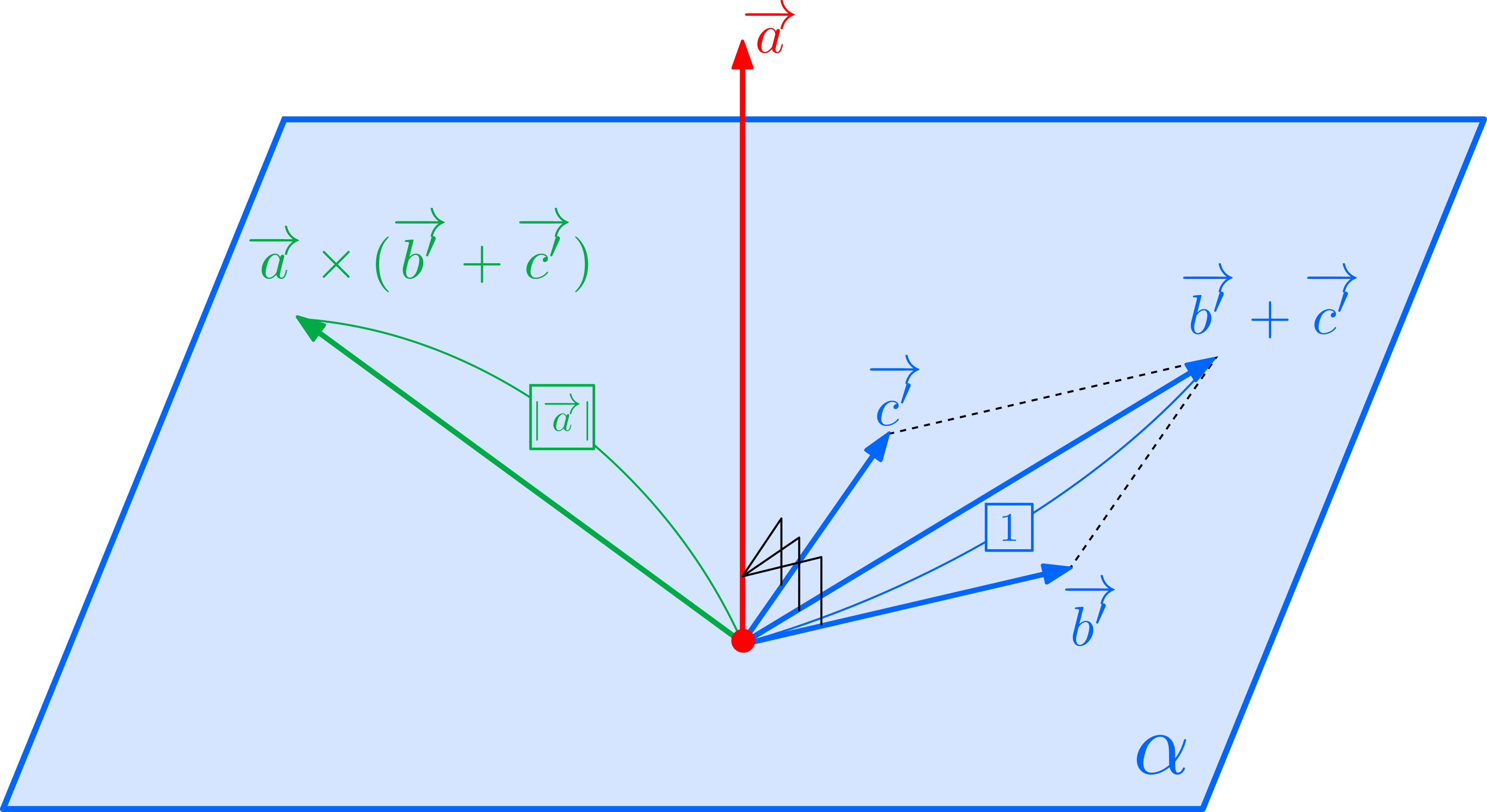
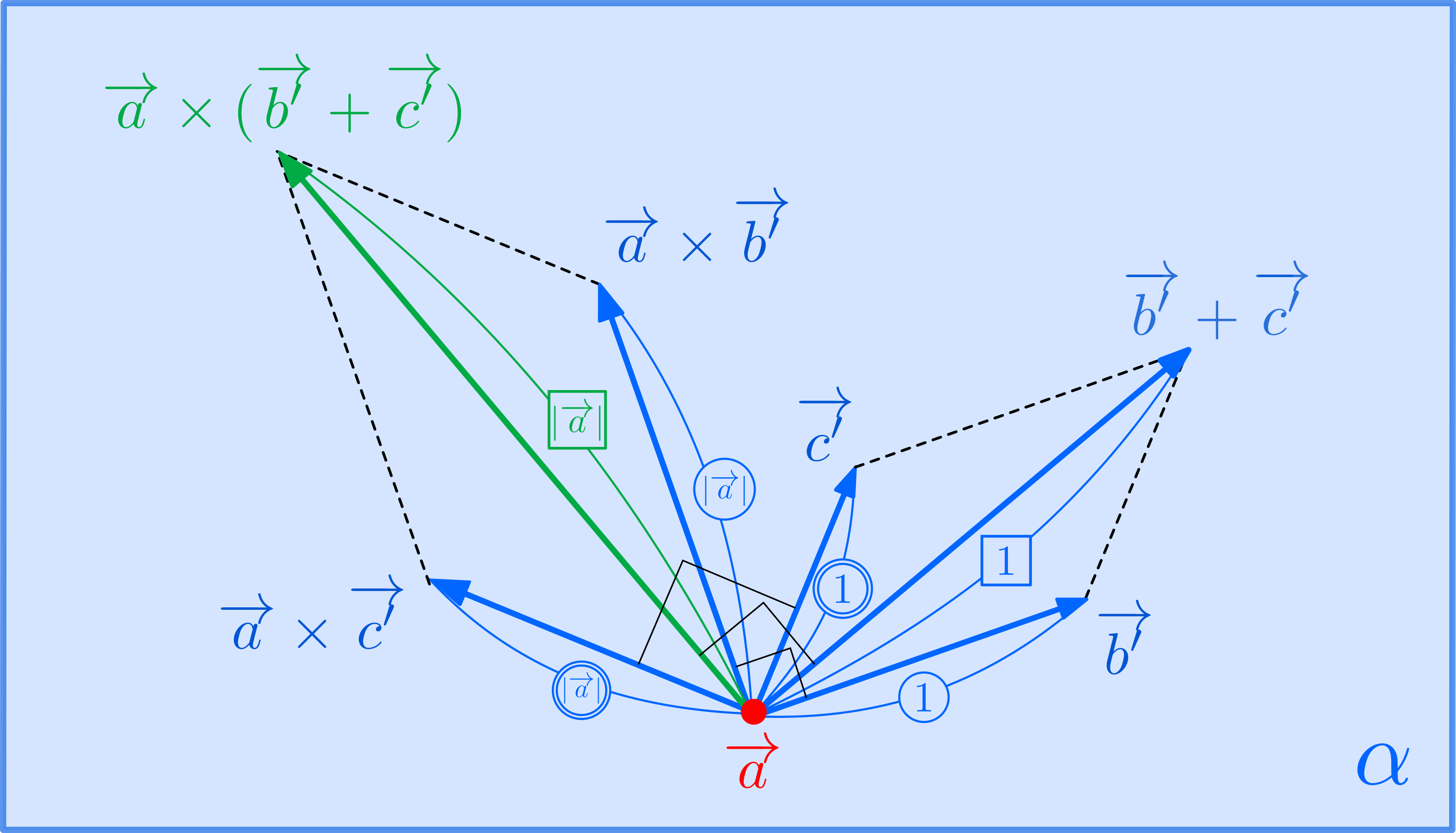
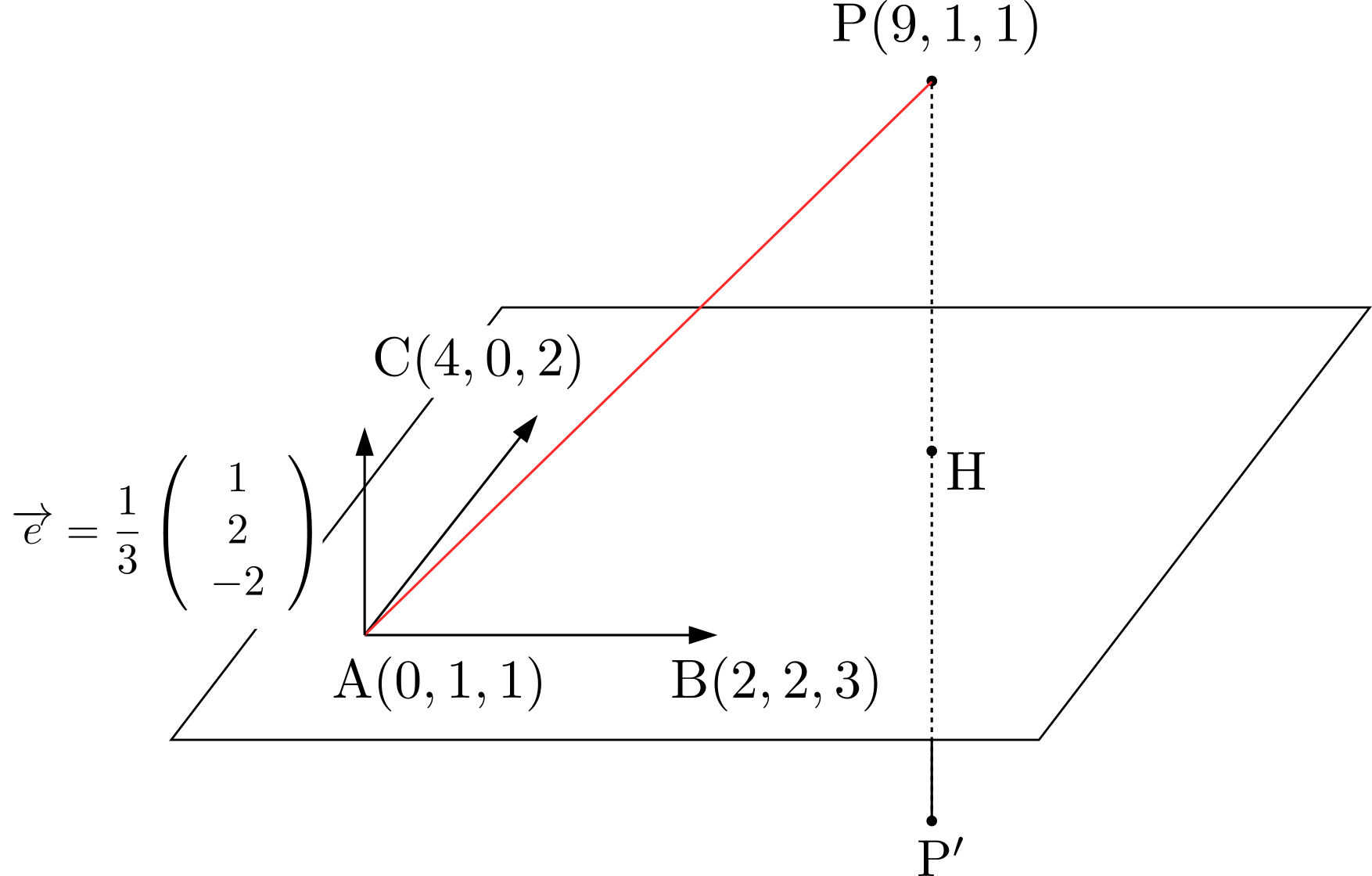
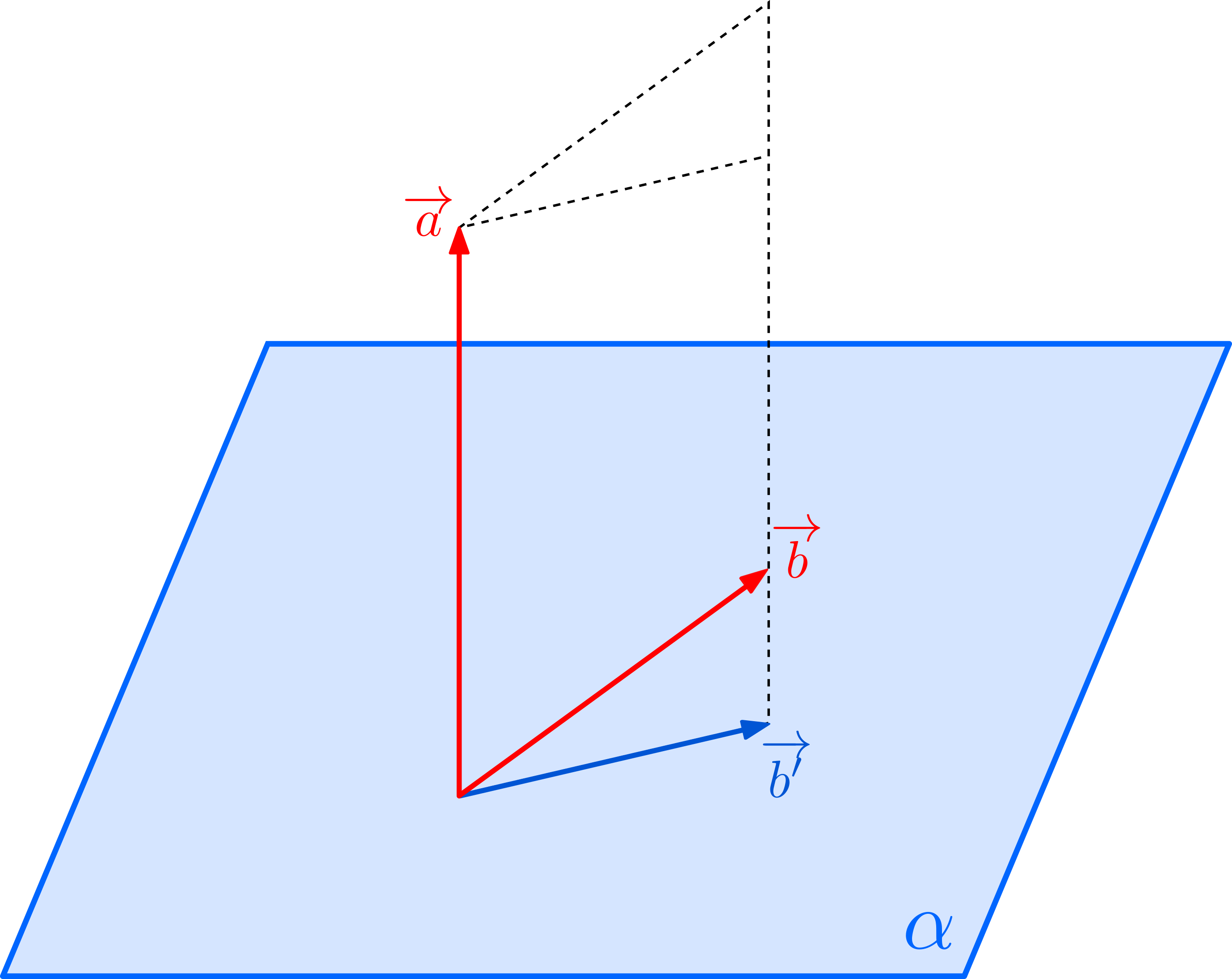 \((3)\)について:
\((3)\)について: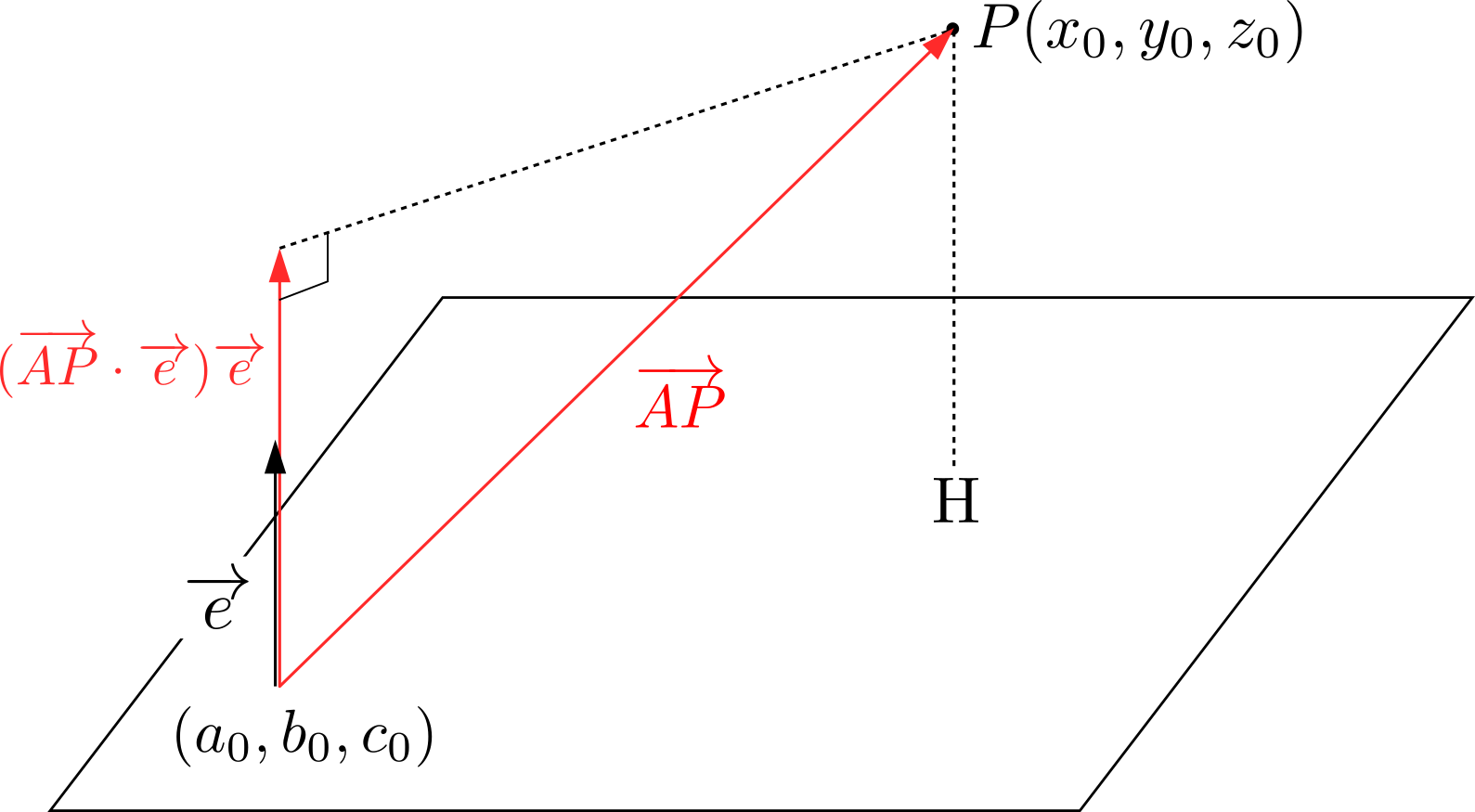 \((a_0,b_0,c_0)\)を平面上の点とする.点\(P\)から平面へおろした足を\(H\)とおけば,線分\(PH\)の長さは
\((a_0,b_0,c_0)\)を平面上の点とする.点\(P\)から平面へおろした足を\(H\)とおけば,線分\(PH\)の長さは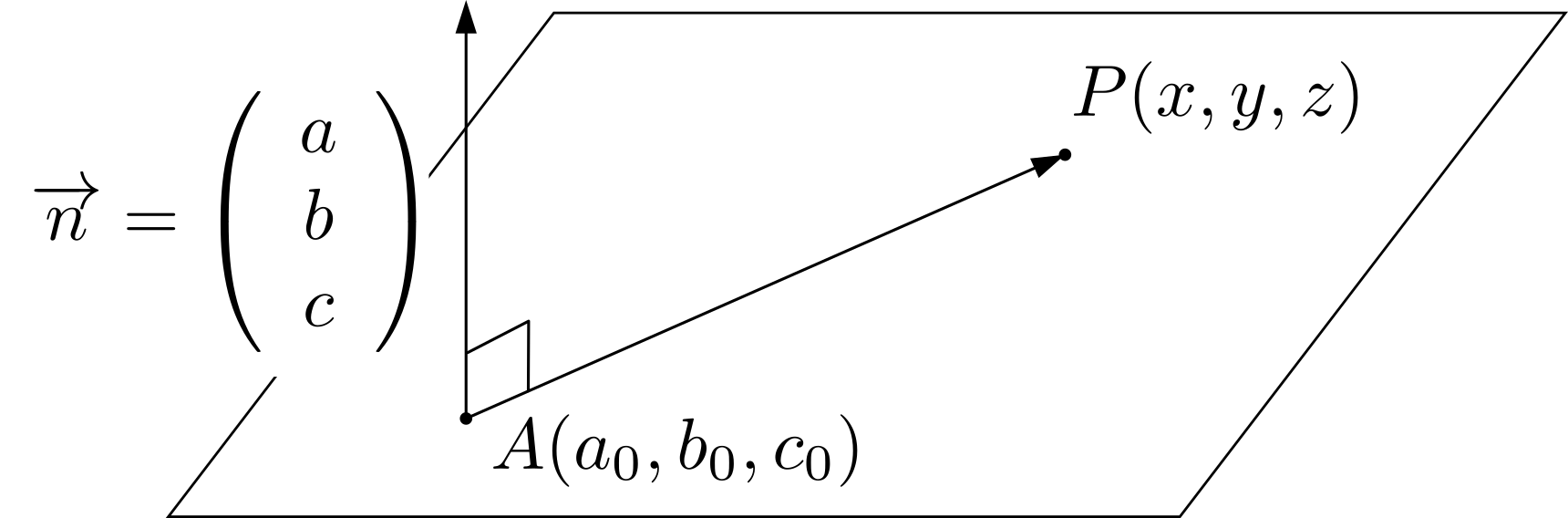 ここでは,平面はその平面の垂直方向とその平面が通る1点が定まれば決定することに着目します。平面の法線ベクトルを\(\overrightarrow{n}=(a,b,c)\),平面が通る1点の座標を\(A(a_0,b_0,c_0)\),平面上の任意の点を\(P(x,y,z)\)とおくことにします。\begin{align*}
ここでは,平面はその平面の垂直方向とその平面が通る1点が定まれば決定することに着目します。平面の法線ベクトルを\(\overrightarrow{n}=(a,b,c)\),平面が通る1点の座標を\(A(a_0,b_0,c_0)\),平面上の任意の点を\(P(x,y,z)\)とおくことにします。\begin{align*}
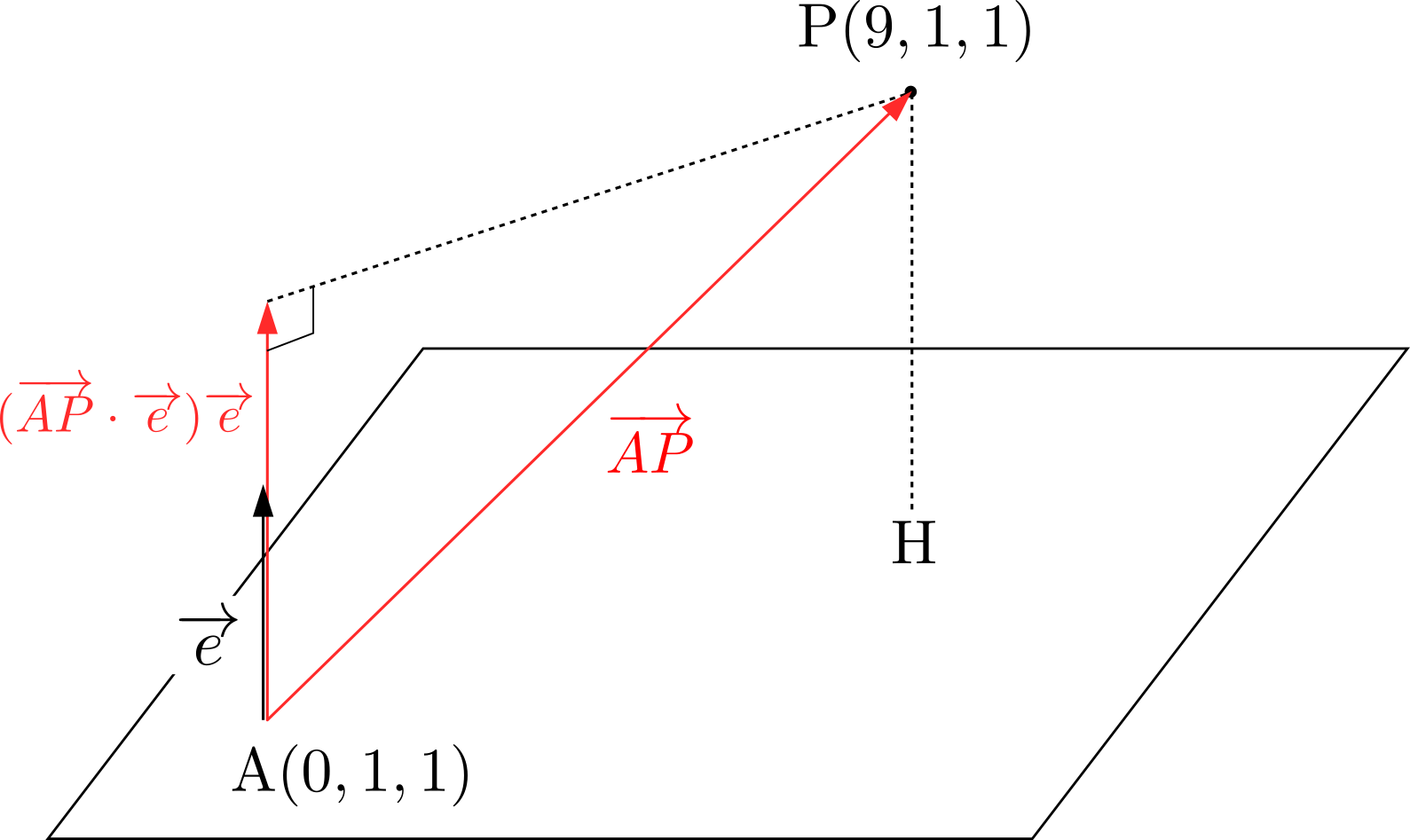 ここで,
ここで,



 このベクトルは始点が既に原点にありますから,位置ベクトル,すなわちその成分と終点が指し示す座標が一致しているはずです.したがって\(\overrightarrow{\mathrm{OH}}\)の終点が指し示す座標を調べればよい.\(\mathrm{OH}=\text{孤}\mathrm{PH}\)であることに注意すると(「滑らずに」転がしたんだから!右図参照),\(\mathrm{OH}=a\theta\).したがって点\(\mathrm{H}\)の座標は\((a\theta,0)\)で,(座標と成分が対応するから)\(\overrightarrow{\mathrm{OH}}\)の成分は\(\left(\begin{array}{c} a\theta \\ 0 \\ \end{array} \right)\)となります.
このベクトルは始点が既に原点にありますから,位置ベクトル,すなわちその成分と終点が指し示す座標が一致しているはずです.したがって\(\overrightarrow{\mathrm{OH}}\)の終点が指し示す座標を調べればよい.\(\mathrm{OH}=\text{孤}\mathrm{PH}\)であることに注意すると(「滑らずに」転がしたんだから!右図参照),\(\mathrm{OH}=a\theta\).したがって点\(\mathrm{H}\)の座標は\((a\theta,0)\)で,(座標と成分が対応するから)\(\overrightarrow{\mathrm{OH}}\)の成分は\(\left(\begin{array}{c} a\theta \\ 0 \\ \end{array} \right)\)となります. 始点が原点にあれば,そのまま終点が指し示す座標を読めばいいのですが,これは始点は原点ではありませんね.しかしベクトルは向きと大きささえ変えさえしなければ自由に動かせるのでしたから,始点を原点にとってから,その終点の座標を読めばよいでしょう.始点を原点にとったときのベクトルの終点が指し示す座標は\((0,~a)\)ですから,そのベクトルの成分は\(\overrightarrow{\mathrm{OH}}\)の成分は\(\left(\begin{array}{c} 0 \\ a \\ \end{array} \right)\)となります.
始点が原点にあれば,そのまま終点が指し示す座標を読めばいいのですが,これは始点は原点ではありませんね.しかしベクトルは向きと大きささえ変えさえしなければ自由に動かせるのでしたから,始点を原点にとってから,その終点の座標を読めばよいでしょう.始点を原点にとったときのベクトルの終点が指し示す座標は\((0,~a)\)ですから,そのベクトルの成分は\(\overrightarrow{\mathrm{OH}}\)の成分は\(\left(\begin{array}{c} 0 \\ a \\ \end{array} \right)\)となります.