カテゴリー: 数学Ⅰ

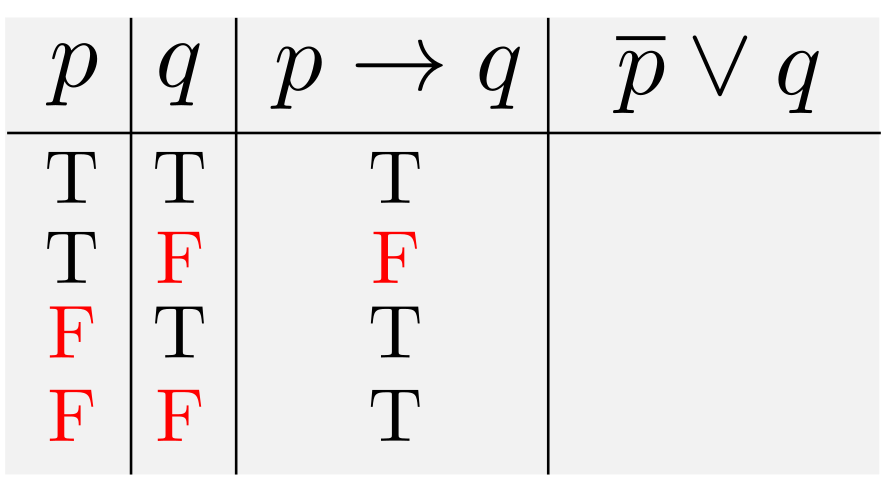
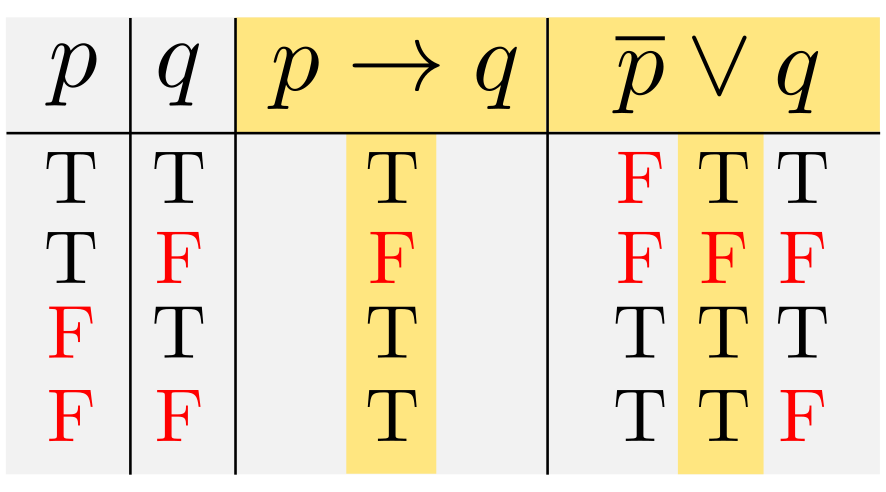
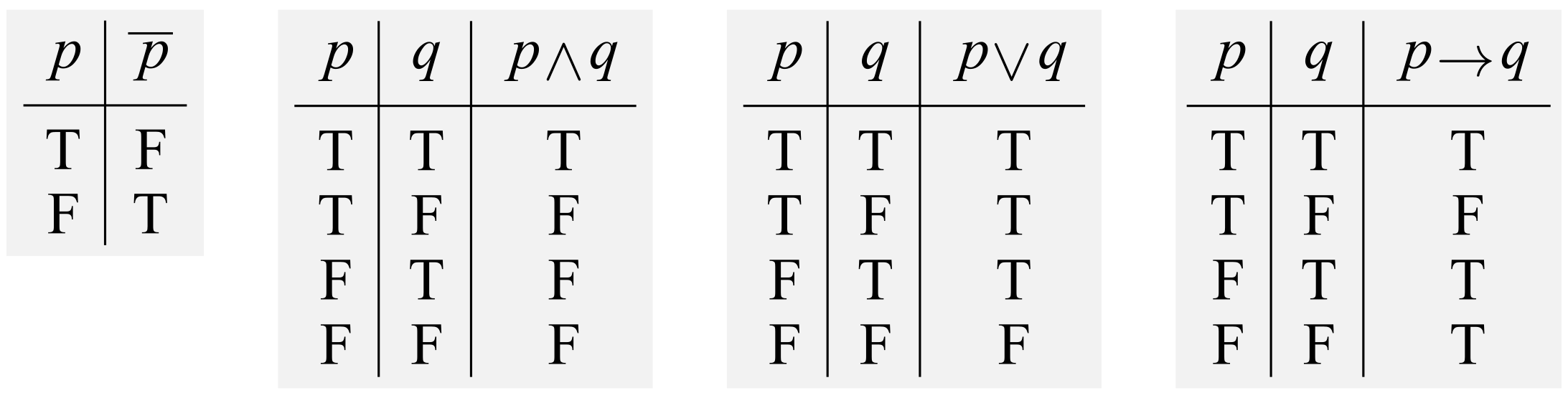
下の記事を見直してたらちょっと気になったので一言．「文字を減らす」という方針について以前の記事に追加です．

です．

（理由）
\(\Rightarrow\)は第１式の\(s\)と\(t\)に第２，３式により\(s=g(x,y),~t=h(x,y)\)をそれぞれ代入すれば得られます．
\(\Leftarrow\)はは第１式の\(g(x,y)\)と\(h(x,y)\)を第２，３式により\(g(x,y)=s,~h(x,y)=t\)とおき直せば得られます．（ちなみにこれは，もし第２，３式\(g(x,y)=s,~h(x,y)=t\)がなければ逆が成り立たない，すなわち
\[
\begin{cases}
f(s,~t)=0\\
s=g(x,y)\\
t=h(x,y)
\end{cases}
\Longrightarrow
f(g(x,y),~h(x,y))=0\\
\]
であることを意味します．）

…（同値性という観点から言えば）文字は別に減らしてなんかいないことに注意．

しかしもし，
\[
\exists s \exists t\begin{cases}
f(s,~t)=0\\
s=g(x,y)\\
t=h(x,y)
\end{cases}
\]
なら，存在記号を処理することで，

となります．見た目通り，文字\(s,t\)は消えます．

\[\exists s \exists t \left[s = \frac{2Y}{2-X} \land t = \frac{X}{2-X} \land s^2=4t \right]\]という主張の同値変形について見てみます．

【変形１】
\begin{align*}
&\exists s \exists t \left[s = \frac{2Y}{2-X} \land t = \frac{X}{2-X} \land s^2=4t \right]&(0)\\
\Longleftrightarrow~&\exists s \exists t \left[s = \frac{2Y}{2-X} \land t = \frac{X}{2-X} \land \frac{4Y^2}{(2-X)^2}=\frac{4X}{2-X}\right]&(1)\\
\Longleftrightarrow~&\exists s \exists t \left[s = \frac{2Y}{2-X} \land t = \frac{X}{2-X} \land Y^2=X(2-X) \land X \neq 2 \right]&(2)\\
\Longleftrightarrow~&\exists s \exists t \left[s = \frac{2Y}{2-X} \land t = \frac{X}{2-X} \right] \land Y^2=X(2-X) \land X \neq 2&(3)\\
\Longleftrightarrow~&X \neq 2 \land Y^2=X(2-X) \land X \neq 2&(4)\\
\Longleftrightarrow~&Y^2=X(2-X) \land X \neq 2&(5)\\
\Longleftrightarrow~&(X-1)^2+Y^2=1 \land X \neq 2
\end{align*}

\((2)\)は\(\frac{4Y^2}{(2-X)^2}=\frac{4X}{2-X} \Longleftrightarrow Y^2=X(2-X) \land X \neq 2\)
\((3)\)は\(Y^2=X(2-X) \land X \neq 2\)が変数\(s,t\)を含まないので，\(\exists s\exists t\)の支配域を変更することができるから
\((4)\)は\(\exists s \exists t \left[s = \frac{2Y}{2-X} \land t = \frac{X}{2-X} \right] \Longleftrightarrow X \neq 2\)より
\((5)\)は
\[p \land q \Leftrightarrow q \land p,\quad p \land p \Leftrightarrow p\]
によります（いずれも真理値表から明らか）

【変形２】
\begin{align*}
&\exists s \exists t \left[s = \frac{2Y}{2-X} \land t = \frac{X}{2-X} \land s^2=4t \right]&(0)’\\
\Longleftrightarrow~&\exists s \left[ \exists t \left[s = \frac{2Y}{2-X} \land t = \frac{X}{2-X} \land s^2=4t\right]\right] &(1)’\\
\Longleftrightarrow~&\exists s \left[s = \frac{2Y}{2-X} \land \exists t\left[ t = \frac{X}{2-X} \land s^2=4t\right]\right] &(2)’\\
\Longleftrightarrow~&\exists s \left[s = \frac{2Y}{2-X} \land s^2=\frac{4X}{2-X}\right] &(3)’\\
\Longleftrightarrow~&\left(\frac{2Y}{2-X}\right)^2=\frac{4X}{2-X} &(4)’\\
\Longleftrightarrow~&Y^2=X(2-X) \land X \neq 2&(5)’\\
\Longleftrightarrow~&(X-1)^2+Y^2=1 \land X \neq 2
\end{align*}

\((1)’\)はそもそも\(\exists s\left[ \exists t[p(s,t)]\right]\)の略記が\(\exists s \exists t[p(s,t)]\)だから
\((2)’\)は支配域の変更．\((2)\)と同じ
\((3)’\)は\(\exists t\)の処理
\((4)’\)は\(\exists s\)の処理
\((5)’\)は\((1)\)と同様の同値変形によります

\((0)’\)から\(~(4)’\)までの同値変形はこのように書くと厳ついですがやってることは結局\(s,t\)の消去です．通常は\((0)’\)から\((4)’\)まで一気に一行で処理してしまうところだと思います．

\((0)\)から\((1)\)への変形と\((0)’\)から\((4)’\)への変形に違いに注意しましょう（詳しくはこの記事にて．関連：「『存在する』の扱い」，「連立方程式の解法は…『文字を減らす』方針？」）．文字を「消去する」ことを正しく認識していないとこういう箇所で間違えてしまうので注意．

【変形１】【変形２】いずれにしても同じ結論です．途中のアプローチが違えど，論理式を正しく扱いすれば必然的に同じ結論が得られる，ということでした．

\(\exists x[a \leq x \leq b] \Longleftrightarrow a\leq b\)

証明

（\(\Rightarrow\)）
存在する\(x\)を\(c\)とおくと，\(a \leq c \leq b\)が成り立つ．ゆえに\(a \leq b\)がいえる．

（\(\Leftarrow\)）
\(a \leq b\)とする．このとき，\(\frac{a+b}{2}\)をとれば，\(a \leq \frac{a+b}{2} \leq b\)とかける．すなわち\(a \leq x \leq b\)をみたす\(x\)が（\(\frac{a+b}{2}\)として）存在する．

（証明終）

この問題で使いました．

教科書では「点\(P\)の軌跡を求める手順」を次のように言っています

1. 1. 条件を満たす点\(P\)の座標を\((x,~y)\)として，点\(P\)に関する条件を\(x,~y\)の式で表し，この方程式が表す図形が何かを調べる．
   2. 逆に，で求めた図形上のすべての点\(P\)が，与えられた条件を満たすことを確かめる．

引用元：『高等学校　数学Ⅱ』数研出版

で，その解法に従った解答が，

点\(P\)に関する条件は\[OP:AP=2:1\]
これより\[2AP=OP\]
すなわち\[4AP^2=OP^2\]
\(AP^2=(x-3)^2+y^2,~OP^2=x^2+y^2\)を代入すると\(4\left\{(x-3)^2+y^2\right\}=x^2+y^2\)
整理すると\(x^2-8x+y^2+12=0\)すなわち\((x-4)^2+y^2=2^2\)．
よって点\(P\)は円\((x-4)^2+y^2=2^2\)上にある．
逆に，この円上のすべての点\(P(x,~y)\)は，条件を満たす．
したがって，求める軌跡は，点\((4,~0)\)を中心とする半径\(2\)の円である．

引用元：『高等学校　数学Ⅱ』数研出版

とあります．ここで疑問．

「逆に，この円上のすべての点\(P(x,~y)\)は，条件を満たす」これは何？っていうか，なぜこんなことが言えるの？実際にその「すべての点」について「距離の比が\(2:1\)である」と調べたってこと？でも「すべての点」って，得られた図形は円だから円上の点，すなわち「無限個の点」ということでしょ？無限回計算して調べるわけ…？？

…と思った人も少なくないはず．これ，疑問を持つほうが自然で，その人の理解力が無いんじゃなく，はっきり言って教科書のほうが悪い．まさに教科書特有のダメダメ記述の代表格．にもかかわらず何のフォローもないという．結果どうするか？「良く分からないから覚えよう」になる．だからあまり深く考えない人ほどテキトーにスルーして得点できる．こんな勉強を強いられる（真面目な）高校生が本当かわいそう．

別解を示します．

解答
\[
\begin{align}
&OP:AP=2:1\\
\Longleftrightarrow &~2AP=OP\\
\Longleftrightarrow &~4AP^2=OP^2\\
\Longleftrightarrow &~4\left\{(x-3)^2+y^2\right\}=x^2+y^2\\
\Longleftrightarrow &~x^2-8x+y^2+12=0\\
\Longleftrightarrow &~(x-4)^2+y^2=2^2\\
\end{align}
\]
したがって，求める軌跡は，点\((4,~0)\)を中心とする半径\(2\)の円．

このようにかけば逆の考察など必要ありません．その理由は，上のように一連の式の間の論理関係を見てらえればわかりますが，どれも同値変形だからです．このような同値記号を用いた記述であれば，このこと，すなわち「各式は明らかに同値だから，逆の考察はしないよ」という意思表示になっています．だから逆の考察は必要ない，というわけです．

対して，教科書の解答はどういう意図のもとに「逆に～」を書いているのでしょうか．解答では「これより」「すなわち」「整理すると」「よって」…という（数学的定義のない）日本語を多用しているところを見るに，各段階において十分性を意識せずに変形している，と考えられます（「最初に十分性を追わずに必要性だけ追っていき，あとで別枠で十分性を調べる」という論法自体は数学ではよく見られる方法で，それ自体は問題はありません）．論理式で書けば

\[
\begin{align}
&OP:AP=2:1\\
\Longrightarrow &~2AP=OP\\
\Longrightarrow &~4AP^2=OP^2\\
\Longrightarrow &~4\left\{(x-3)^2+y^2\right\}=x^2+y^2\\
\Longrightarrow &~x^2-8x+y^2+12=0\\
\Longrightarrow &~(x-4)^2+y^2=2^2\\
\end{align}
\]

という構造になっているので，最後に元の条件と同値であるかどうか確認が求められる，だから上の論理式において「\(\Leftarrow\)も言えるよ」という意味で「逆に，この円上のすべての点\(P(x,~y)\)は，条件を満たす．」と書いたのでしょう．しかしこれもかなり譲歩して読み取ればの話で，解答の書き方では冒頭に記したように「\((x-4)^2+y^2=2^2\)をみたすすべての点，つまり無限個の点について距離の比が\(2:1\)であると無限回調べた」としか読み取れないと思うんですがね．

もちろん教科書特有の色々な制約の下でのやむを得ない記述なんでしょうけど，正直者が馬鹿を見る（真面目な；思慮深い生徒が躓く）的な記述はいかがなものか，と思う．せめて解答欄外でフォローしようよ，と思いますね．これだから教科書至上主義は危険です．

「いやそんなややこしいこと考えずともに最後に『逆に～』の一言を書いときゃそれでOKでしょ点数は貰えるし」と思う人．それは教科書レベルでの話．少し発展的な問題になると痛い目にあいますよ．

網羅系問題集には必ず載ってる軌跡の有名問題です．この手の問題に難儀した人は少なくないと思います．初めて見る人はこれを教科書で学んだ方法で解答を作成してみましょう．正解ならOK（軌跡に「漏れ」や「余計なもの」が入っていたらそれは正解とはいいませんよ）．不正解なら以下を読んでみてください．

論理式で記述してみます．

求める軌跡上の点を\((X,~Y)\)とします．「\((X,~Y)\)が軌跡上の点である」ということを「\((X,~Y)\in\text{軌跡}\)」と表すことにします．この「\((X,~Y)\in\text{軌跡}\)」を同値変形することを考えます．

\[
\begin{align*}
&(X,~Y)\in\text{軌跡}\\
\Longleftrightarrow~&\exists k\begin{cases}
kX+2Y-k+4=0\\
2X-kY+6-2k=0
\end{cases}\tag{1}\\
\Longleftrightarrow~&\exists k\begin{cases}
(X-1)k=-2Y-4\\
2X-kY+6-2k=0
\end{cases}\\
\Longleftrightarrow~&\exists k\begin{cases}
(X-1)k=-2Y-4\land(X-1=0 \lor X-1\neq 0)\\
2X-kY+6-2k=0\tag{2}
\end{cases}\\
\Longleftrightarrow~&\exists k\begin{cases}
((X-1)k=-2Y-4\land X-1=0) \lor ((X-1)k=-2Y-4\land X-1\neq 0)\\
2X-kY+6-2k=0\tag{3}
\end{cases}\\
\Longleftrightarrow~&\exists k\begin{cases}
(0\cdot k=-2Y-4\land X=1) \lor (k=\frac{-2Y-4}{X-1}\land X\neq 1)\\
2X-kY+6-2k=0
\end{cases}\\
\Longleftrightarrow~&\exists k\begin{cases}
(X=1\land Y=-2) \lor (k=\frac{-2Y-4}{X-1}\land X\neq 1)\\
2X-kY+6-2k=0
\end{cases}\\
\Longleftrightarrow~&\exists k\left(((X=1\land Y=-2) \lor (k=\frac{-2Y-4}{X-1}\land X\neq 1))\land 2X-kY+6-2k=0\right)\\
\Longleftrightarrow~&\exists k\left((X=1\land Y=-2\land 2X-kY+6-2k=0) \lor (k=\frac{-2Y-4}{X-1}\land X\neq 1\land 2X-kY+6-2k=0)\right)\tag{4}\\
\Longleftrightarrow~&\exists k(X=1\land Y=-2\land 2X-kY+6-2k=0) \lor \exists k(k=\frac{-2Y-4}{X-1}\land X\neq 1\land 2X-kY+6-2k=0)\tag{5}\\
\Longleftrightarrow~&\exists k(X=1\land Y=-2\land 2\cdot 1-k\cdot (-2)+6-2k=0) \lor (X\neq 1\land 2X-\frac{-2Y-4}{X-1}Y+6-2\frac{-2Y-4}{X-1}=0)\tag{6}\\
\Longleftrightarrow~&\exists k(X=1\land Y=-2\land 0\cdot k+8=0) \lor (X\neq 1\land X^2+2X+Y^2+4Y+1=0)\tag{7}\\
\Longleftrightarrow~&X\neq 1\land (X+1)^2+(Y+2)^2=4\tag{8}\\
\end{align*}
\]

となって求める軌跡の方程式を得ます．通常の解答を見るとわかりますが，読めばとりあえず理解はできるものの，いざ自分で解答をつくれと言われると次に何をやればよいのか見えずらく（必然性が感じられず）不安に感じるタイプの問題ではないでしょうか．で，結局半ば流れを「覚えよう」となるっていう．しかし，上で見るように論理式で記述すると機械的な変形（次にすべきことが明解で迷いがない，もはや「計算」するような感覚）により答えを得ることがきます．これが論理式の強力な点だと思います．

ただし上の変形は論理に関する様々な知識を使っています．

\((1)\)は存在条件への言い換えです．
\((2)\)は恒真条件\(X-1=0\lor X-1\neq 0\)の追加
\((3)\)は分配法則
\((4)\)は分配法則
\((5)\)は存在記号の分配法則
\((6)\)後半は存在記号があるので\(k\)を消去できて
\((7)\)の前半は矛盾命題なので\((8)\)と同値になります．

（というか数式がはみ出て見づらくてすみません…）

できます（かつ（\(\land\)）に関して）．なぜなら，

\[\forall x[p(x)\land q(x)]~\Longleftrightarrow \forall x p(x)\land \forall x q(x)\]であるから，この命題の待遇を考えると，

\[\lnot(\forall x[p(x)\land q(x)])~\Longleftrightarrow \lnot(\forall x p(x)\land \forall x q(x))\]

すなわち

\[\exists x[\lnot p(x)\lor \lnot q(x)]~\Longleftrightarrow \exists x \lnot p(x)\lor \exists x \lnot q(x)\]

となります．\(\lnot\)は否定を表す記号です．ですから，

\[\exists x[\overline{p(x)}\lor \overline{q(x)}]~\Longleftrightarrow \exists x \overline{ p(x)}\lor \exists x \overline{q(x)}\]

とも書けますね．見やすさのために\(\overline{p(x)}\)を\(p(x)\)に，\(\overline{q(x)}\)を\(q(x)\)に改めて書き換えれば，
\[\exists x[p(x) \lor q(x)]~\Longleftrightarrow \exists x p(x)\lor \exists x q(x)\]
となります．

注意：ただし，存在記号はかつ（\(\land\)）に関しては分配できません！すなわち，\[\exists x[p(x) \land q(x)] \Longrightarrow \exists x p(x) \land \exists xq(x)\]であって，この逆は成り立ちません．これは具体例を考えれば分かりやすい．仮に全体集合をあるクラスだとして，\(p(x)\)を「\(x\)は勉強が得意」\(q(x)\)を「\(x\)はスポーツが得意」だとします．すると，\(\exists x[p(x) \land q(x)]\)は「勉強もスポーツも両方得意な生徒がいる」となり，\(\exists x p(x) \land \exists xq(x)\)は「勉強が得意な生徒がいて，かつ，スポーツが得意な生徒もいる」となります．\(\Longrightarrow\)が成り立つのは当たり前でしょう．\(\Longleftarrow\)について考えます．「（そのクラスに）勉強が得意な生徒がいて，スポーツが得意な生徒もいるのなら，勉強もスポーツも両方得意な生徒がいる」となりますが，これは正しいでしょうか．少し考えればわかるように明らかに正しくないですね．反例．仮定を満たすクラスとして，「勉強は超得意だけどスポーツはダメダメな秀才君がいて，スポーツは超得意だけど勉強はからっきしの脳筋君がいる．そしてクラスの他の生徒たちは勉強もスポーツもとくに得意とは言えない，いたってフツーの生徒，そんなクラスが例えば考えられます．このクラスには明らかに「勉強もスポーツも両方得意な生徒」はいることにはなりませんね．