とある軌跡の問題の模範解答に関して次のような質問がありました.
模範解答では,\(X=\frac{16m^2}{4m^2+1}\)を得たのち
\[\text{「\(m^2<\frac{1}{12}\)を満たす実数の存在条件は\(0 \leq m^2<\frac{1}{12}\)だから,\(0 \leq X <1\)」}\]
とあるが,これは論理的にはどのように導いたのか?
模範解答だとたしかに何をやっているのか,というか何をいっているのかよくわかりません.
そこで論理式で考えます.模範解答の論理の流れはおそらくは以下です(代入法による解答との分岐点は\((1)\)からです):
\begin{align*}
&\exists m \left[X=\frac{16m^2}{4m^2+1} \land Y=m(X-4)\land m^2<\frac{1}{12}\right]\\
\Longleftrightarrow~&\exists m\left[X=\frac{16m^2}{4m^2+1} \land Y=m(X-4)\land m^2<\frac{1}{12} \land (X=4 \lor X \neq 4)\right]\\
\Longleftrightarrow~&\exists m\left[\left(X=\frac{16m^2}{4m^2+1} \land Y=m(X-4)\land 0\leq m^2<\frac{1}{12} \land X=4 \right)\right.\\
&\lor \left.\left(X=\frac{16m^2}{4m^2+1} \land Y=m(X-4)\land m^2<\frac{1}{12} \land X \neq 4\right)\right]\\
\Longleftrightarrow~&\exists m\left[X=\frac{16m^2}{4m^2+1} \land m=\frac{Y}{X-4}\land m^2<\frac{1}{12} \land X \neq 4\right]\tag{0}\\
\Longleftrightarrow~&\exists m\left[X=\frac{16m^2}{4m^2+1} \land m=\frac{Y}{X-4}\land m^2<\frac{1}{12} \land X \neq 4 \land \exists t\geq 0 [t=m^2]\right]\tag{1}\\
\Longleftrightarrow~&\exists m\left[X=\frac{16m^2}{4m^2+1} \land m=\frac{Y}{X-4}\land m^2<\frac{1}{12} \land X \neq 4 \land \exists t[t\geq 0 \land t=m^2]\right]\tag{2}\\
\Longleftrightarrow~&\exists m \exists t\left[X=\frac{16m^2}{4m^2+1} \land m=\frac{Y}{X-4}\land m^2<\frac{1}{12} \land X \neq 4 \land t \geq 0 \land t=m^2\right]\tag{3}\\
\Longleftrightarrow~&\exists m \exists t\left[X=\frac{16t}{4t+1} \land m=\frac{Y}{X-4}\land t<\frac{1}{12} \land X \neq 4 \land t \geq 0 \land t=m^2\right]\tag{4}\\
\Longleftrightarrow~&\exists t\left[t=\frac{1}{4}\left(\frac{X}{4-X}\right) \land 0\leq t<\frac{1}{12} \land X \neq 4 \land t=\left(\frac{Y}{X-4}\right)^2\right]\tag{5}\\
\Longleftrightarrow~&0\leq \frac{1}{4}\left(\frac{X}{4-X}\right)<\frac{1}{12} \land X \neq 4 \land \frac{1}{4}\left(\frac{X}{4-X}\right)=\left(\frac{Y}{X-4}\right)^2\tag{6}\\
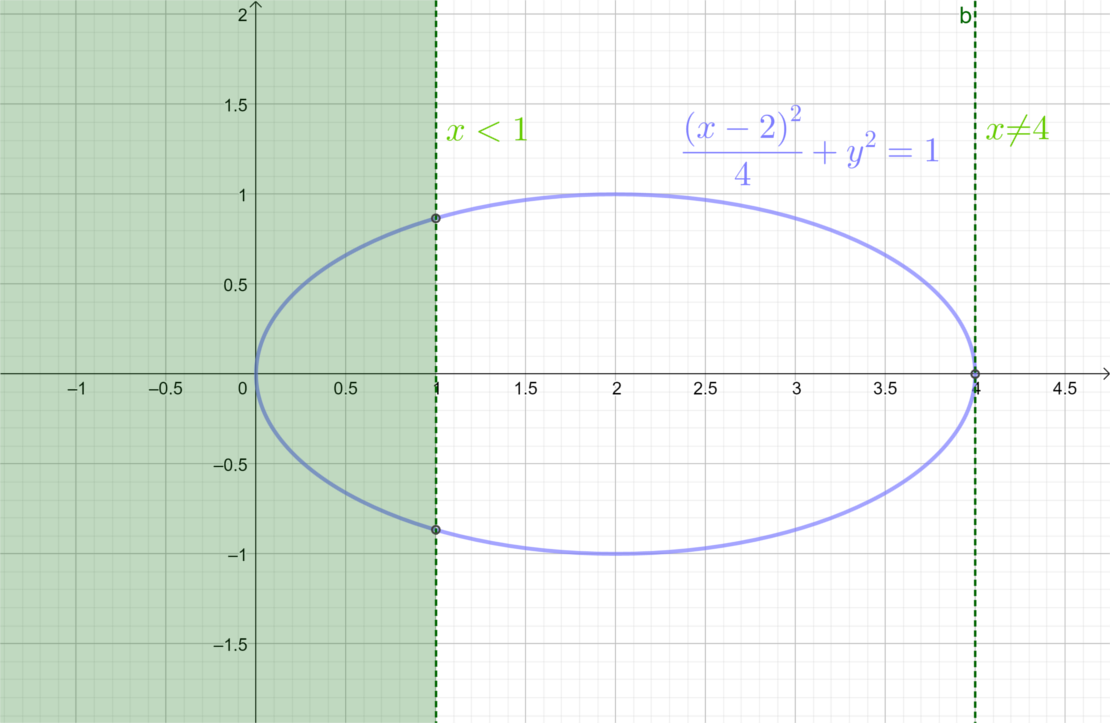
\Longleftrightarrow~&\frac{(X-2)^2}{4}+Y^2 = 1 \land 0 \leq X < 1 \land X \neq 4 \\
\Longleftrightarrow~&\frac{(X-2)^2}{4}+Y^2 = 1 \land 0 \leq X < 1
\end{align*}
\((0)\)ここまでこれと同じ
\((1)\)恒真条件\(\exists t \geq 0 [t=m^2]\)の追加.\(\exists m\)の支配域の下で考えているので,当然\(m^2\)すなわち\(0\)以上の\(t\)が存在しますから,恒真条件です.
\((2)\)略記の書き直し
\((3)\)\(\exists t\)の支配域の変更.自分\((t=m^2)\)以外はどれも変数\(t\)を含んでいないのでいちばん外側に追い出せます.
\((4)\)代入法(\(m^2\)に\(t\)を代入)
\((5)\)\(\exists m\)の処理
\((6)\)\(\exists t\)の処理
こうしてみると,模範解答での「(\(X=\frac{16m^2}{4m^2+1}\)において)\(m^2<\frac{1}{12}\)を満たす実数の存在条件は\(0 \leq m^2<\frac{1}{12}\)だから,\(0 \leq X <1\)」とは,厳密には以下のような操作を指して言っているのだと分かります:
-
- \(m^2\)を\(t\)とおき\(\left((0) \Leftrightarrow (1)\right)\),
- 支配域の変更を経て\(\left((3)\right)\),
- 代入法により\(X=\frac{16t}{4t+1}\left(\Leftrightarrow t=\frac{1}{4}\left(\frac{X}{4-X}\right)\right)\)と(★)\(0\leq t<\frac{1}{12}\)が出現するわけですが\(\left((4)\right)\),
- 前者は\(t\)についての1次式ですから,\(\exists t\)により\(t\)を同値変形として「消去」できて,\(\left((5) \Leftrightarrow (6)\right)\)
- 結果,(★★)同値性を保ったまま\(0 \leq X < 1\)が得られる.
模範解答にある
\[\text{「\(m^2<\frac{1}{12}\)を満たす実数の存在条件は\(0 \leq m^2<\frac{1}{12}\)だから,」}\]
に対応する部分が(★),そして
\[\text{「\(0 \leq X <1\)」}\]
に対応する部分が(★★),であろうとおそらくは考えられます.…確かに,このような内容になると「端折る」ことも必要になってくるのかもしれません.
他方,次のような「置き換え」をしない変形も考えられます.
(別解釈)
\begin{align*}
&\exists m \left[X=\frac{16m^2}{4m^2+1} \land Y=m(X-4)\land m^2<\frac{1}{12}\right]\\
\Longleftrightarrow~&\exists m\left[X=\frac{16m^2}{4m^2+1} \land Y=m(X-4)\land m^2<\frac{1}{12} \land (X=4 \lor X \neq 4)\right]\\
\Longleftrightarrow~&\exists m\left[\left(X=\frac{16m^2}{4m^2+1} \land Y=m(X-4)\land m^2<\frac{1}{12} \land X=4 \right)\right.\\
&\lor \left.\left(X=\frac{16m^2}{4m^2+1} \land Y=m(X-4)\land m^2<\frac{1}{12} \land X \neq 4\right)\right]\\
\Longleftrightarrow~&\exists m\left[X=\frac{16m^2}{4m^2+1} \land m=\frac{Y}{X-4}\land m^2<\frac{1}{12} \land X \neq 4\right] \tag{0}\\
\Longleftrightarrow~&\exists m\left[m^2=\frac{1}{4}\left(\frac{X}{4-X}\right)\land m=\frac{Y}{X-4}\land m^2<\frac{1}{12} \land X \neq 4 \right] \tag{1}\\
\Longleftrightarrow~&\exists m \left[m^2=\frac{1}{4}\left(\frac{X}{4-X}\right) \land m=\frac{Y}{X-4}\land \frac{1}{4}\left(\frac{X}{4-X}\right)<\frac{1}{12} \land X \neq 4 \right]\tag{2}\\
\Longleftrightarrow~&\left(\frac{Y}{X-4}\right)^2=\frac{1}{4}\left(\frac{X}{4-X}\right) \land \frac{1}{4}\left(\frac{X}{4-X}\right)<\frac{1}{12} \land X \neq 4 \tag{3}\\
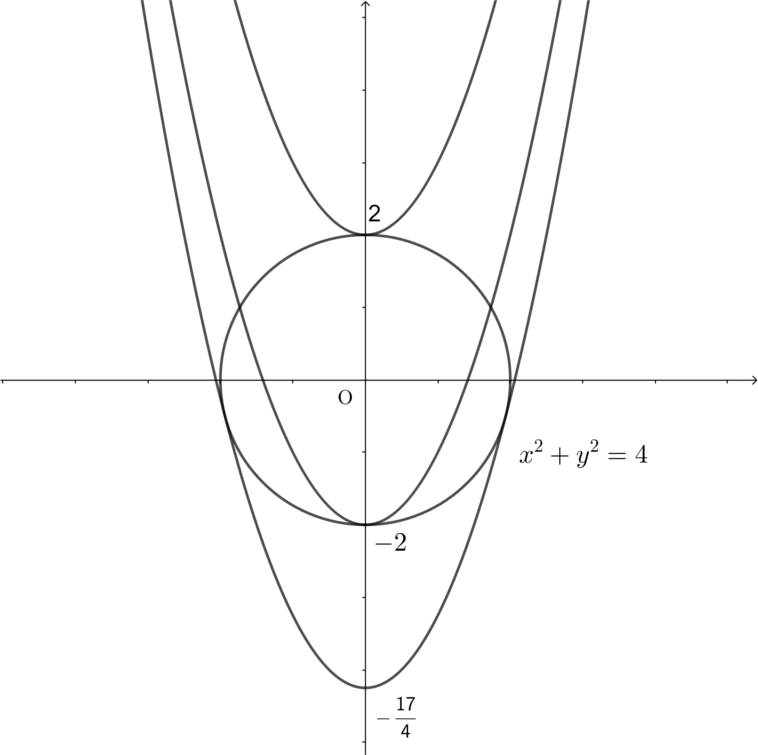
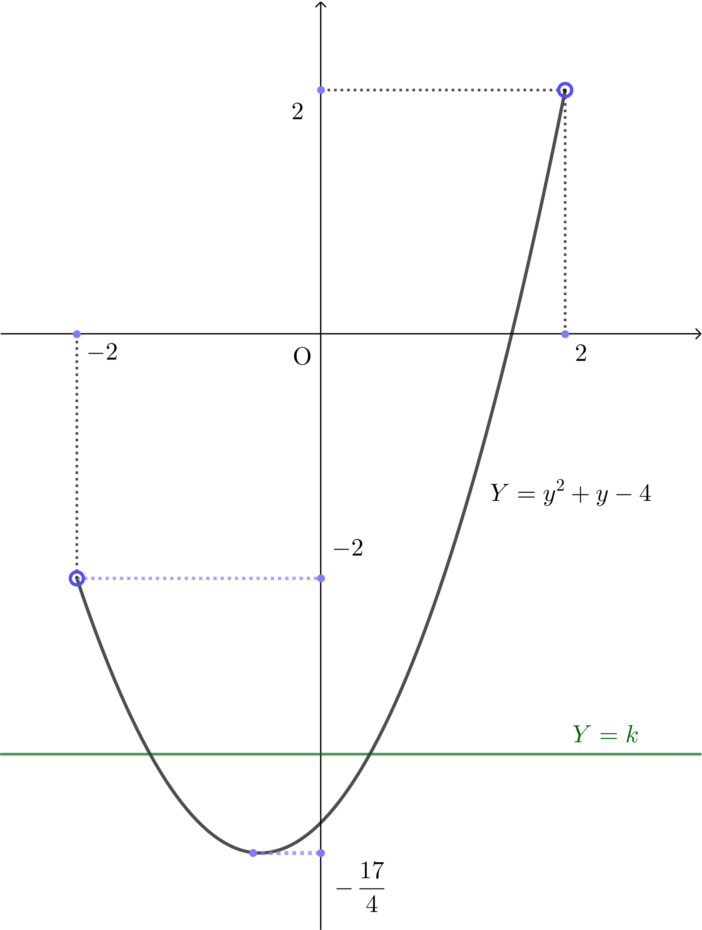
\Longleftrightarrow~&\frac{(X-2)^2}{4}+Y^2 = 1 \land (X < 1 \lor 4 < X) \land X \neq 4\\
\Longleftrightarrow~&\left(\frac{(X-2)^2}{4}+Y^2 = 1 \land X \neq 4 \land X < 1 \right) \lor \left( \frac{(X-2)^2}{4}+Y^2 = 1\land X \neq 4 \land 4 < X \right) \\
\Longleftrightarrow~&\frac{(X-2)^2}{4}+Y^2 = 1 \land X \neq 4 \land X < 1 \tag{\(\ast\)}\\
\Longleftrightarrow~&\frac{(X-2)^2}{4}+Y^2 = 1 \land 0 \leq X < 1 \tag{\(\ast\)}
\end{align*}
\((1)\)は第一式を\(m^2\)について解いた
\((2)\)代入法
\((3)\)\(\exists m\)の処理
\((\ast)\)は下図による.