天下りですが以下のような\(2\)変数関数\(B(p,~q)\)を定義します.
ベータ関数\[\displaystyle B(p,~q):=\int^1_0x^{p-1}(1-x)^{q-1}dx\]
(「\(:=\)」は「左辺を右辺で定義する」という意味です.)
この関数をベータ関数と呼びます.こいつを計算してみましょう.
直接的に求まりそうにないので,部分積分してみます(\(x^{p-1}\)を積分側,\((1-x)^{q-1}\)を微分側にしましょう).すると,
\[\displaystyle
\begin{align*}
&\int^1_0 x^{p-1}(1-x)^{q-1}dx\\
=&\biggl[\frac{x^p}{p}(1-x)^{q-1}\biggl]^1_0+\int^1_0\frac{x^p}{p}(q-1)(1-x)^{q-2}dx\\
=&\frac{q-1}{p}\int^1_0x^p(1-x)^{q-2}dx\\
=&\frac{q-1}{p}B(p+1,~q-1)
\end{align*}
\]
より,
\[B(p,~q)=\frac{q-1}{p}B(p+1,~q-1)\]という漸化式を得ます.この漸化式から,
\[
\begin{align*}
&B(p,~q)=\frac{q-1}{p}B(p+1,~q-1)\\
&B(p+1,~q-1)=\frac{q-2}{p+1}B(p+2,~q-2)\\
&B(p+2,~q-2)=\frac{q-3}{p+2}B(p+3,~q-3)\\
&B(p+3,~q-3)=\frac{q-4}{p+3}B(p+4,~q-4)\\
&\hspace{40mm}\vdots
\end{align*}
\]
が得られますが,例えば上の四つの式から,
\[B(p,~q)=\frac{q-1}{p}\frac{q-2}{p+1}\frac{q-3}{p+2}\frac{q-4}{p+3}B(p+4,~q-4)\]
が得られますので,この調子で続ければ\(B(\text{☆},\text{★})\)の\(\text{★}\)がどんどん小さくなり,うまく計算が出来そうです.
では,★はどこまで下げましょうか?\(B(\text{☆},\text{★})\)の定義をみると,★は1であると計算しやすいですね.なぜなら\((1-x)^{q-1}\)が\(0\)乗で1になってくれますから.
\(B(\text{☆},\text{★})\)の\(\text{★}\)が1になるまで下げてみます.
\[
\begin{align*}
&B(p,~q)=\frac{q-1}{p}B(p+1,~q-1)\\
&B(p+1,~q-1)=\frac{q-2}{p+1}B(p+2,~q-2)\\
&B(p+2,~q-2)=\frac{q-3}{p+2}B(p+3,~q-3)\\
&B(p+3,~q-3)=\frac{q-4}{p+3}B(p+4,~q-4)\\
&\hspace{40mm}\vdots\\
&B(p+(q-2),~q-(q-2))=\frac{q-(q-1)}{p+(q-2)}B(p+(q-1),~q-(q-1))
\end{align*}
\]
(4行目の\(\displaystyle B(p+3,~q-3)=\frac{q-4}{p+3}B(p+4,~q-4)\)の「\(4\)」を「\(q-1\)」に,「\(3\)」を「\(q-2\)」に置き換えるイメージ!)
したがって,
\[
\begin{align*}
B(p,~q)&=\frac{q-1}{p}\frac{q-2}{p+1}\frac{q-3}{p+2}\frac{q-4}{p+3}~\cdots~\frac{q-(q-1)}{p+(q-2)}B(p+(q-1),~q-(q-1)\\
&=\frac{q-1}{p}\frac{q-2}{p+1}\frac{q-3}{p+2}\frac{q-4}{p+3}~\cdots~\frac{1}{p+q-2}B(p+q-1,~1)\\
&=\frac{(p-1)!(q-1)!}{(p+q-2)!}B(p+q-1,~1)\\
&=\frac{(p-1)!(q-1)!}{(p+q-2)!}\int^1_0x^{p+q-2}(1-x)^0dx\\
&=\frac{(p-1)!(q-1)!}{(p+q-2)!}\int^1_0x^{p+q-2}dx\\
&=\frac{(p-1)!(q-1)!}{(p+q-2)!}\biggl[\frac{x^{p+q-1}}{p+q-1}\bigg]^1_0\\
&=\frac{(p-1)!(q-1)!}{(p+q-1)!}
\end{align*}
\]
できました.\(\displaystyle B(p,~q)=\frac{(p-1)!(q-1)!}{(p+q-1)!}\).定義より\(\displaystyle B(p,~q)=\int^1_0x^{p-1}(1-x)^{q-1}dx\)でしたから,結局,
\[\displaystyle \int^1_0x^{p-1}(1-x)^{q-1}dx=\frac{(p-1)!(q-1)!}{(p+q-1)!}\]
が得られたことになります.
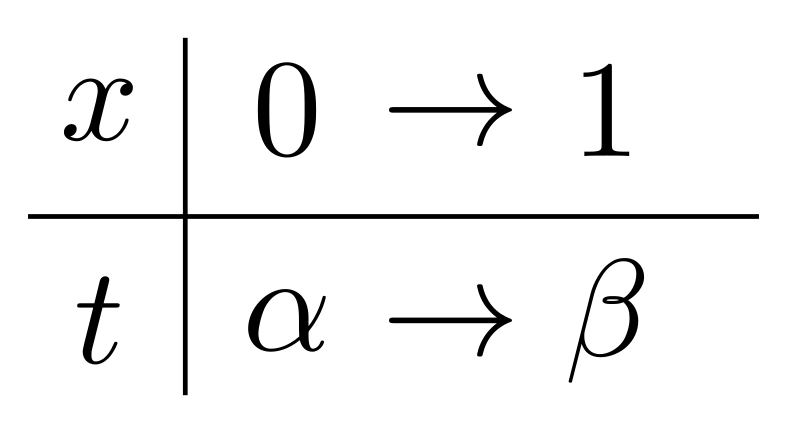 さて次に,\(\displaystyle \int^1_0x^{p-1}(1-x)^{q-1}dx\)の積分区間\([0,~1]\)が,\([\alpha,~\beta]\)となるような置換を考えてみましょう.すなわち右のような置換です(新たな変数\(t\)としました).この場合,どのように置換すればよいでしょうか?\(t\)が\(\alpha\)のとき\(x\)が\(0\)ですから,さしあたり\[x=t-\alpha\]という置換が思い浮かびます.しかし,\(t=\beta\)のとき\(x\)は\(\beta-\alpha\)ではなく\(1\)であってほしい.であれば,\(t-\alpha\)を\(\beta-\alpha\)で割ればいいのでは?と考え,\[\displaystyle x=\frac{t-\alpha}{\beta-\alpha}\]という置換に気付きます.置換してみましょう.\(\displaystyle dx=\frac{1}{\beta-\alpha}dt\)ですから,
さて次に,\(\displaystyle \int^1_0x^{p-1}(1-x)^{q-1}dx\)の積分区間\([0,~1]\)が,\([\alpha,~\beta]\)となるような置換を考えてみましょう.すなわち右のような置換です(新たな変数\(t\)としました).この場合,どのように置換すればよいでしょうか?\(t\)が\(\alpha\)のとき\(x\)が\(0\)ですから,さしあたり\[x=t-\alpha\]という置換が思い浮かびます.しかし,\(t=\beta\)のとき\(x\)は\(\beta-\alpha\)ではなく\(1\)であってほしい.であれば,\(t-\alpha\)を\(\beta-\alpha\)で割ればいいのでは?と考え,\[\displaystyle x=\frac{t-\alpha}{\beta-\alpha}\]という置換に気付きます.置換してみましょう.\(\displaystyle dx=\frac{1}{\beta-\alpha}dt\)ですから,
\[
\begin{align*}
\displaystyle \int^1_0x^{p-1}(1-x)^{q-1}dx&=\int^{\beta}_{\alpha}\left(\frac{t-\alpha}{\beta-\alpha}\right)^{p-1}\left(1-\frac{t-\alpha}{\beta-\alpha}\right)^{q-1}\frac{1}{\beta-\alpha}dt\\
&=\frac{1}{(\beta-\alpha)^{p+q-1}}\int^{\beta}_{\alpha}(t-\alpha)^{p-1}(\beta-t)^{q-1}dt
\end{align*}
\]
ゆえに,
\[\displaystyle \frac{1}{(\beta-\alpha)^{p+q-1}}\int^{\beta}_{\alpha}(x-\alpha)^{p-1}(\beta-x)^{q-1}dx=\frac{(p-1)!(q-1)!}{(p+q-1)!}\]
すなわち,
\[\displaystyle \int^{\beta}_{\alpha}(x-\alpha)^{p-1}(\beta-x)^{q-1}dx=\frac{(p-1)!(q-1)!}{(p+q-1)!}(\beta-\alpha)^{p+q-1}\]
が得られたことになります(ダミー変数を\(t\)から見慣れた\(x\)に変えました).
…で,結局何がいいたいの??というと…
この式の\((p,~q)\)に例えば\((2,~2),~(2,~3)\)と代入してみてください.前者は
\[\displaystyle \int^{\beta}_{\alpha}(x-\alpha)(\beta-x)dx=\frac{1}{6}(\beta-\alpha)^3\]
後者は
\[\displaystyle \int^{\beta}_{\alpha}(x-\alpha)(\beta-x)^2dx=\frac{1}{12}(\beta-\alpha)^4\]
となり,例の有名公式が得られます.つまり,数学Ⅱで学ぶ例の有名公式は,実はベータ関数の特殊な場合でもあった,ということがわかります.
このベータ関数は大学の微分積分学で学ぶかと思いますが,実は今回のこの記事の内容自体が大学入試問題として出題されたこともあります.実際,上の解説を見て分かるように導出には部分積分,漸化式,置換積分と高校数学範囲の知識しか使っていません.


 問題
問題


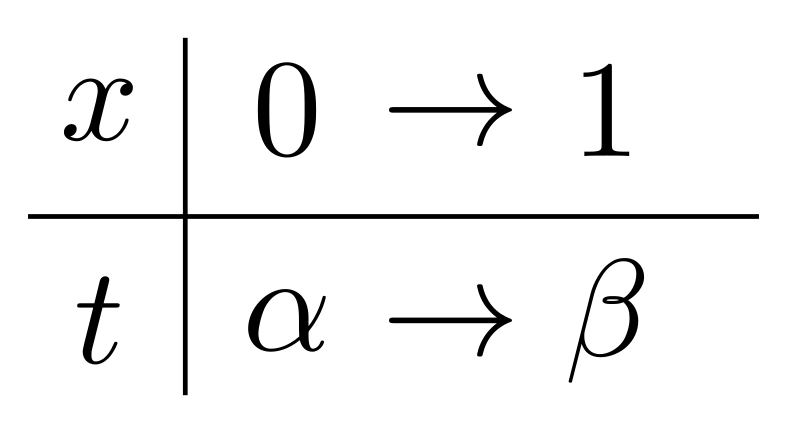 さて次に,\(\displaystyle \int^1_0x^{p-1}(1-x)^{q-1}dx\)の積分区間\([0,~1]\)が,\([\alpha,~\beta]\)となるような置換を考えてみましょう.すなわち右のような置換です(新たな変数\(t\)としました).この場合,どのように置換すればよいでしょうか?\(t\)が\(\alpha\)のとき\(x\)が\(0\)ですから,さしあたり\[x=t-\alpha\]という置換が思い浮かびます.しかし,\(t=\beta\)のとき\(x\)は\(\beta-\alpha\)ではなく\(1\)であってほしい.であれば,\(t-\alpha\)を\(\beta-\alpha\)で割ればいいのでは?と考え,\[\displaystyle x=\frac{t-\alpha}{\beta-\alpha}\]という置換に気付きます.置換してみましょう.\(\displaystyle dx=\frac{1}{\beta-\alpha}dt\)ですから,
さて次に,\(\displaystyle \int^1_0x^{p-1}(1-x)^{q-1}dx\)の積分区間\([0,~1]\)が,\([\alpha,~\beta]\)となるような置換を考えてみましょう.すなわち右のような置換です(新たな変数\(t\)としました).この場合,どのように置換すればよいでしょうか?\(t\)が\(\alpha\)のとき\(x\)が\(0\)ですから,さしあたり\[x=t-\alpha\]という置換が思い浮かびます.しかし,\(t=\beta\)のとき\(x\)は\(\beta-\alpha\)ではなく\(1\)であってほしい.であれば,\(t-\alpha\)を\(\beta-\alpha\)で割ればいいのでは?と考え,\[\displaystyle x=\frac{t-\alpha}{\beta-\alpha}\]という置換に気付きます.置換してみましょう.\(\displaystyle dx=\frac{1}{\beta-\alpha}dt\)ですから,




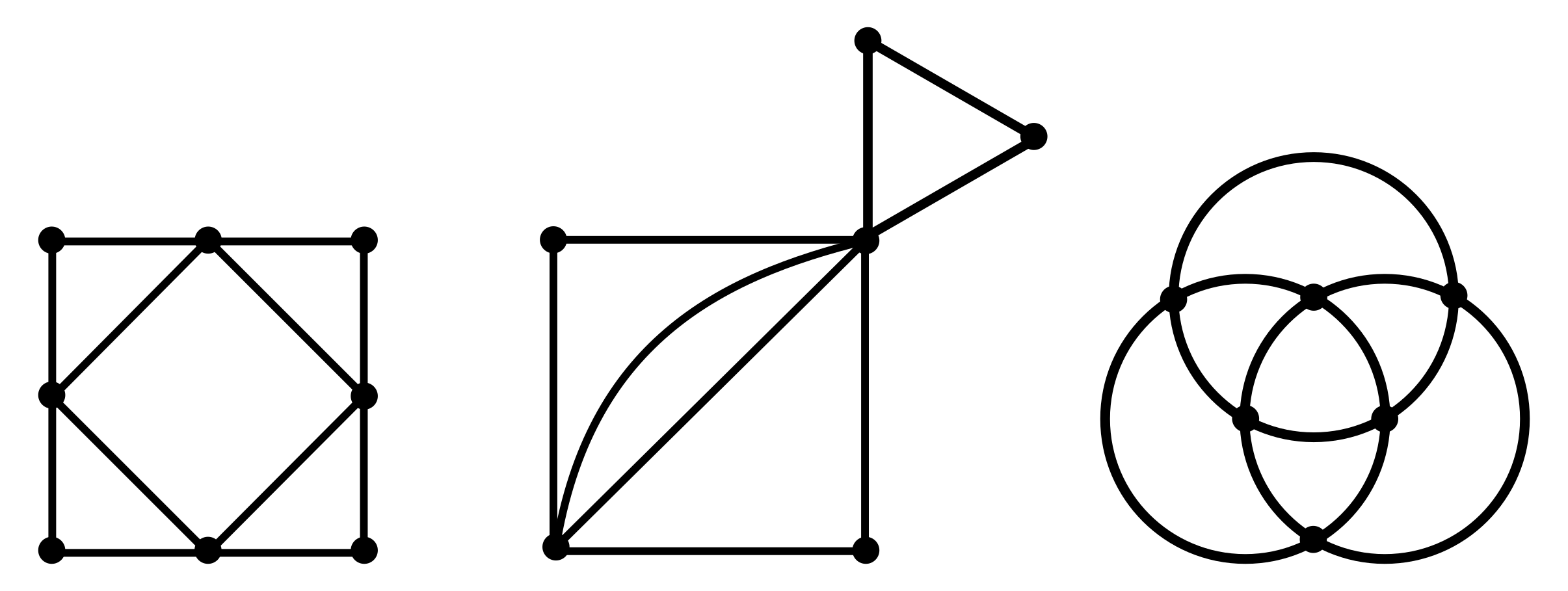
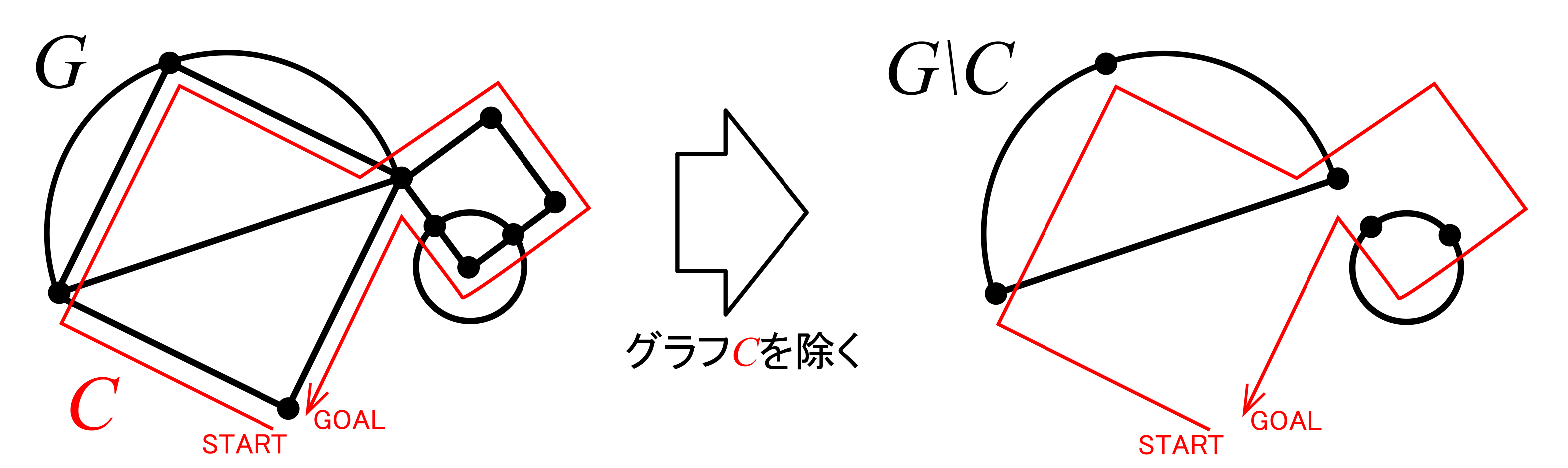
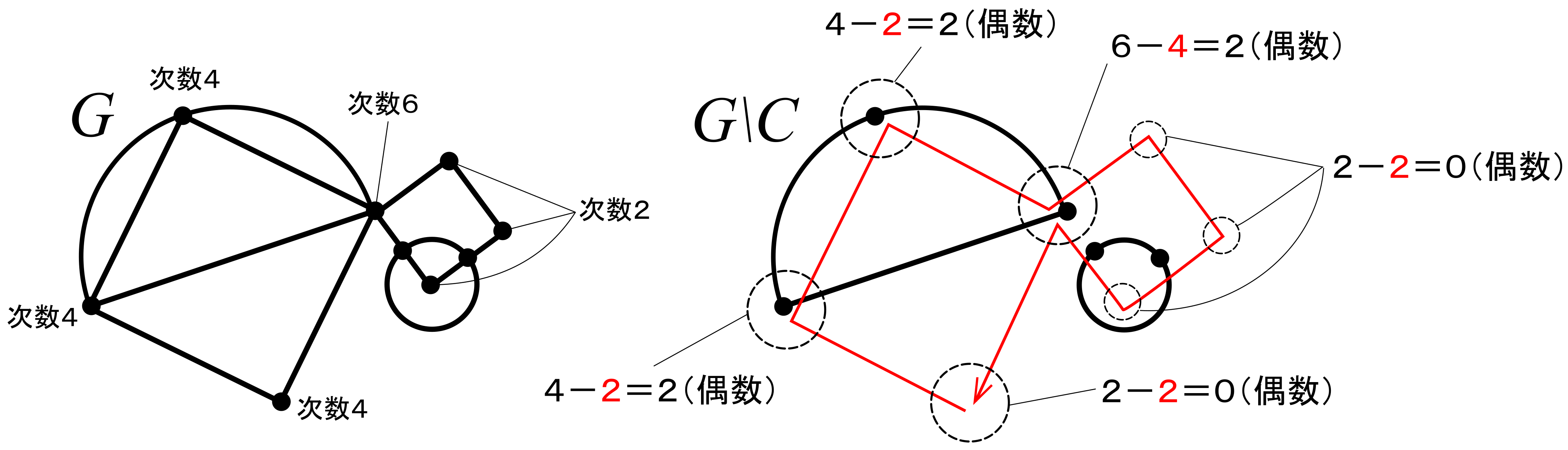
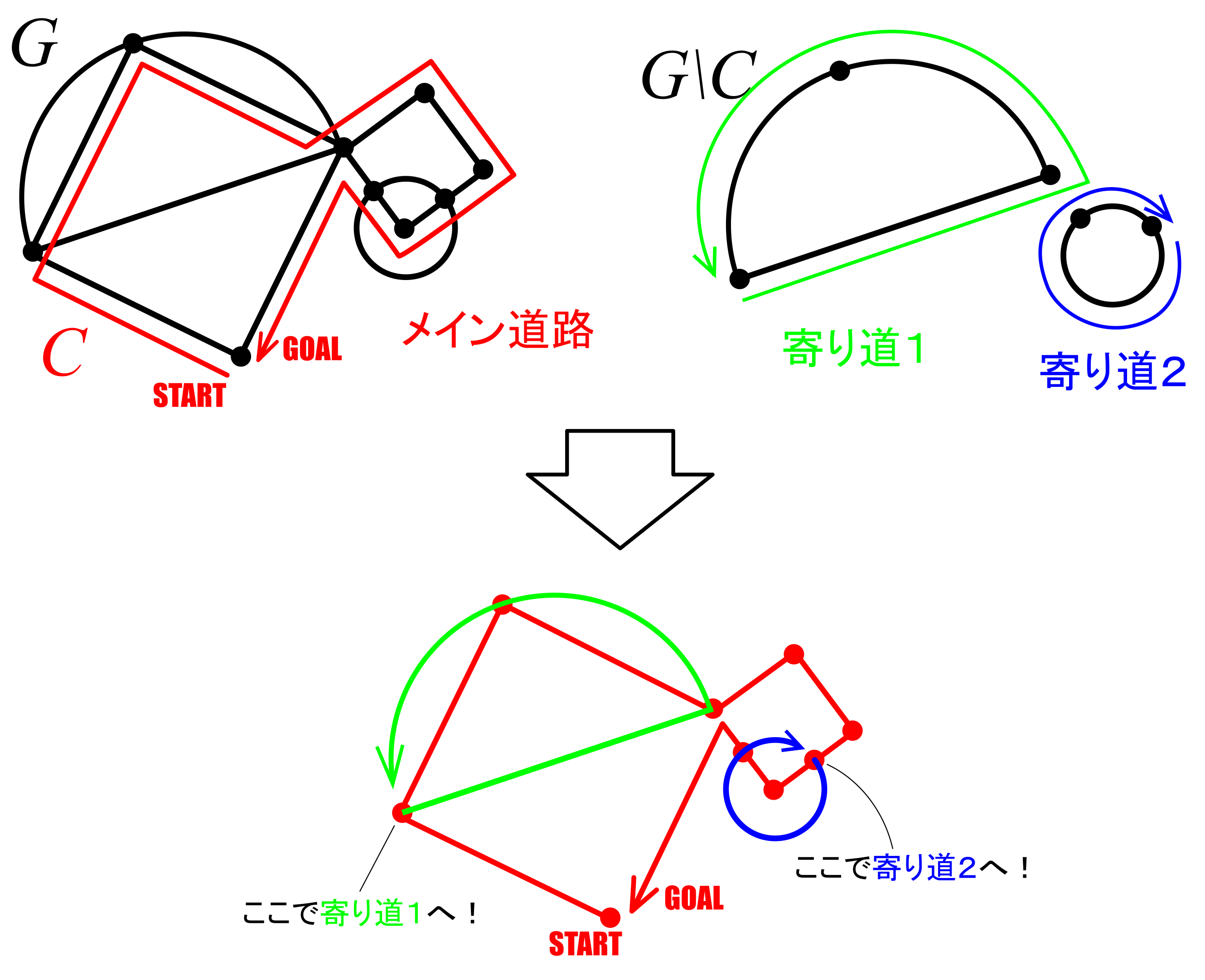
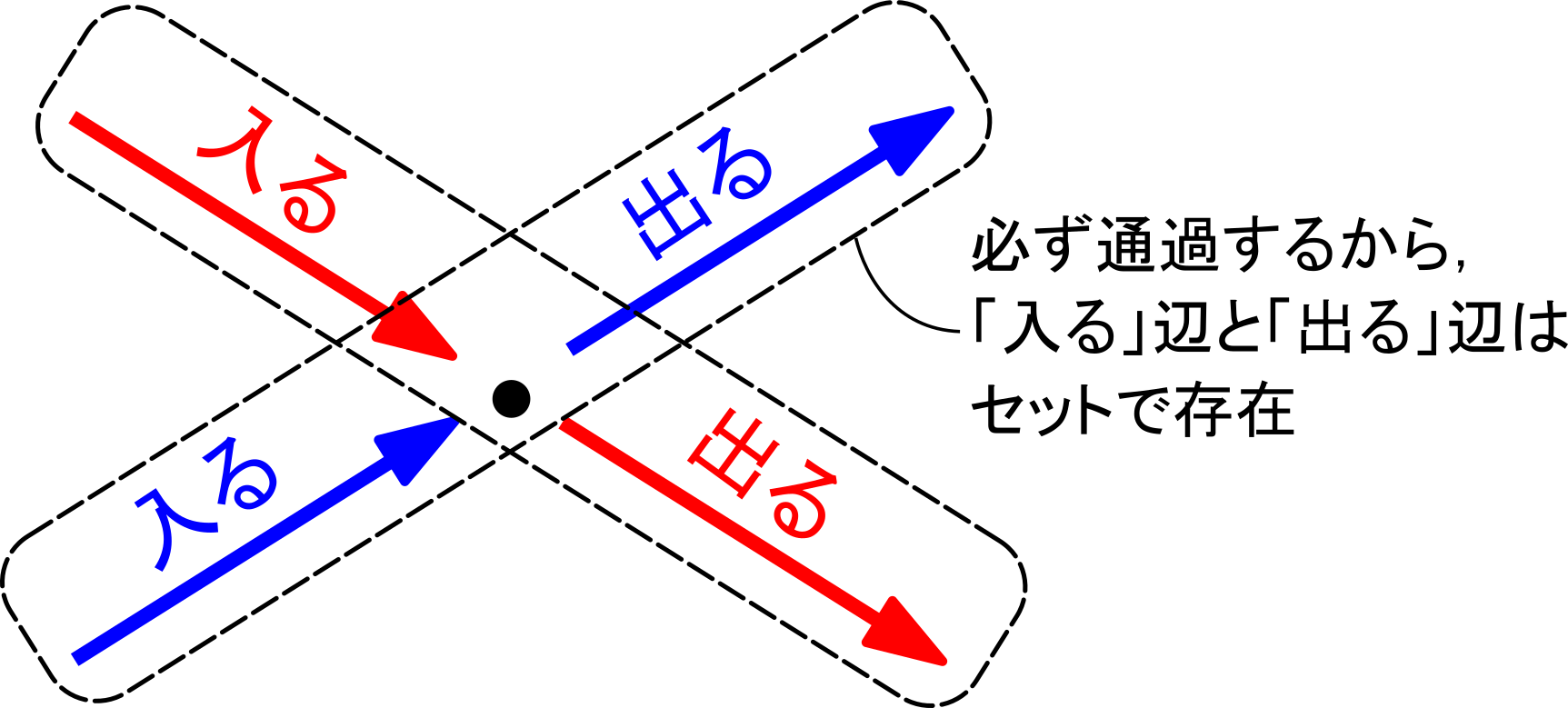 グラフがオイラーグラフであるとする.オイラーグラフとはいわば「一筆書きして出発点に戻ってこられる」ようなグラフであるから,各頂点において,その頂点で袋小路になることなく通過できることになる.これはその頂点に「入る」辺があれば必ず「出ていく」辺もセットで存在することを意味する(2本がセットとなる).したがって各頂点における次数は2の倍数となる.ゆえに,すべての頂点は偶点であるといえる.
グラフがオイラーグラフであるとする.オイラーグラフとはいわば「一筆書きして出発点に戻ってこられる」ようなグラフであるから,各頂点において,その頂点で袋小路になることなく通過できることになる.これはその頂点に「入る」辺があれば必ず「出ていく」辺もセットで存在することを意味する(2本がセットとなる).したがって各頂点における次数は2の倍数となる.ゆえに,すべての頂点は偶点であるといえる.