カテゴリー: 大学数学

投稿日:

★解析演習（アルキメデスの公理）

\(a\)が正の定数で，\(n\)が自然数ならば，
\[\text{\(n \rightarrow \infty\)のとき\(\frac{a}{n} \rightarrow 0\)，すなわち\(\lim_{n \rightarrow \infty}\frac{a}{n}=0\)}\]
であることをアルキメデスの公理から導け．（田島一郎 解析入門 P19問10）

（証明）
示したいことは，\(a>0,~n\in \mathbb{N}\)であるから，
\[
\begin{align*}
&\forall \epsilon>0 \exists m \left[n>m \Longrightarrow \left|\frac{a}{n}-0\right|<\epsilon \right]\\ \Longleftrightarrow~&\forall \epsilon>0 \exists m \left[n>m \Longrightarrow \frac{a}{n}<\epsilon \right]\\ \Longleftrightarrow~&\forall \epsilon>0 \exists m \big[n>m \Longrightarrow n\epsilon >a \big]\tag{\(\ast\)}\\
\end{align*}
\]である．

ここで，アルキメデスの公理とは，\(h\)を正の定数として，
\[\forall K>0 \exists N \big[n>N \Longrightarrow nh > K \big]\]
というものであった．

今，この公理における大前提として与えられている正の定数\(h\)を\(\epsilon\)であるとする．すなわち
\[\forall K>0 \exists N \big[n>N \Longrightarrow n\epsilon > K \big]\]
\(K\)は任意であるから，\(K=a\)とすると，この\(a\)に対応して\(N\)が存在して，
\[n>N \Longrightarrow n\epsilon > a\]
が成り立つと言える\((\ast\ast)\)．

ここで改めて\((\ast)\)について考える．\(\epsilon\)は任意に与えられるわけだが，いちど与えらえた以上それは定数であることに注意すると，結局
\[n>m \Longrightarrow n\epsilon >a\]
をみたす\(m\)の存在を示せばよいが，これは\((\ast\ast)\)により\(m=N\)と提示できる．（証明終）

投稿日:

★解析学演習（はさみうちの原理）

\(x_n \leq a_n \leq y_n\)であって，\(\displaystyle \lim_{n \rightarrow \infty}x_n=\lim_{n \rightarrow \infty}y_n=a\)であれば，\(\displaystyle \lim_{n \rightarrow \infty}a_n=a\)であることを証明せよ．（はさみうちの原理）
（田島一郎 解析入門 P14問7）

（証明）

仮定より，
\[\forall \epsilon >0 \exists N_1\big[n>N_1 \Longrightarrow |x_n-a|<\epsilon \big]\] \[\forall \epsilon >0 \exists N_2\big[n>N_2 \Longrightarrow |y_n-a|<\epsilon \big]\] であるから，\(N=max\{N_1,~N_2\}\)ととれば，\(n>N\)のとき，
\[|x_n-a|<\epsilon,\quad|y_n-a|<\epsilon\]
すなわち
\[a-\epsilon < x_n < a+\epsilon,\quad a-\epsilon < y_n < a+\epsilon\]
これと仮定\(x_n \leq a_n \leq y_n\)から
\[a-\epsilon < x_n \leq a_n \leq y_n < a+\epsilon\]
より
\[a-\epsilon < a_n < a+\epsilon \Longleftrightarrow |a_n-a|<\epsilon\] が言える．以上まとめると， \[\forall \epsilon >0 \exists N\big[n>N \Longrightarrow |x_n-a|<\epsilon \big]\]
すなわち
\[\lim_{n \rightarrow \infty}a_n=a\]
となる．（証明終）

投稿日:

★解析学演習

\(\displaystyle \lim_{n\rightarrow \infty}x_n=a,~\lim_{n\rightarrow \infty}y_n=b\)のとき，\[(1)\quad\lim_{n\rightarrow \infty}x_ny_n=ab\hspace{30mm}(2)\quad\lim_{n\rightarrow \infty}\frac{x_n}{y_n}=\frac{a}{b}\]を示せ．\((2)\)では\(y_n\neq 0,~b\neq 0\)とする．

仮定は
\[\forall \epsilon>0 \exists N_1 \big[n>N_1 \Longrightarrow |x_n-a|<\epsilon\big]\tag{ア}\] および \[\forall \epsilon>0 \exists N_2 \big[n>N_2 \Longrightarrow |y_n-b|<\epsilon\big]\tag{イ}\]
である．

\((1)\)の証明（割愛）

\((2)\)の証明

\(\displaystyle \frac{x_n}{y_n}=x_n\cdot\frac{1}{y_n}\)だから，もし\(\displaystyle\lim_{n\rightarrow \infty}\frac{1}{y_n}=\frac{1}{b}\)が証明できれば，\((2)\)より
\[\lim_{n\rightarrow \infty}\frac{x_n}{y_n}=\lim_{n\rightarrow \infty}x_n\cdot\frac{1}{y_n}=a\cdot\frac{1}{b}=\frac{a}{b}\]
となり証明が完了する．以下，その証明：

示したいことは
\[\forall \epsilon>0 \exists N \left[n>N \Longrightarrow \left|\frac{1}{y_n}-\frac{1}{b}\right|<\epsilon\right]\]
である．一部計算すると，
\[
\begin{align*}
\left|\frac{1}{y_n}-\frac{1}{b}\right|&=\left|\frac{b-y_n}{by_n}\right|=\frac{|y_n-b|}{|b||y_n|}
\end{align*}
\]
より
\[\forall \epsilon>0 \exists N \left[n>N \Longrightarrow \frac{|y_n-b|}{|b||y_n|}<\epsilon\right]\tag{\(\ast\)}\]
である．

任意に与えれらた\(\epsilon\)に対して\(n>N_2\)とすれば，仮定（イ）により\(\displaystyle \frac{|y_n-b|}{|b||y_n|}<\frac{\epsilon}{|b||y_n|}\)と言えるが，しかしそれだけでは分母に\(y_n\)（\(n\)の式）が残っていて\(\epsilon\)（を含む定数）にならない．そこで仮定（イ）において，\(\epsilon\)として\(\displaystyle \epsilon < \frac{|b|}{2}\)をみたす\(\epsilon\)をとる．この\(\epsilon\)に対応する番号\(n\)を\(N’\)とする．すると\(n>N’\)をみたす\(n\)に対して
\[|y_n-b|<\epsilon<\frac{|b|}{2}\]
すなわち
\[b-\frac{|b|}{2} < y_n < b+\frac{|b|}{2}\]
が成り立つ．この式を以下のように考え，変形する：

\(b\geq 0\)のとき，\(b\)の\(\epsilon(<\frac{|b|}{2})\)近傍はすべて正だからそこに入る\(y_n~(n>N’)\)たちももちろん正．ゆえに\(y_n=|y_n|\)．また，\(b=|b|\)．したがって，
\[
\begin{align*}
&b-\frac{|b|}{2} < y_n < b + \frac{|b|}{2}\\
\Longleftrightarrow~&|b|-\frac{|b|}{2} < |y_n| < |b| + \frac{|b|}{2}\\
\Longleftrightarrow~&\frac{|b|}{2} < |y_n| < \frac{3}{2}|b|
\end{align*}
\]

\(b < 0\)のとき，\(b\)の\(\epsilon(<\frac{|b|}{2})\)近傍はすべて負だからそこに入る\(y_n~(n>N’)\)たちももちろん負．ゆえに\(-y_n=|y_n|\)．また，\(b=-|b|\)．したがって，
\[
\begin{align*}
&b-\frac{|b|}{2} < y_n < b + \frac{|b|}{2}\\
\Longleftrightarrow~&-|b|-\frac{|b|}{2} < -|y_n| < -|b| + \frac{|b|}{2}\\
\Longleftrightarrow~&-\frac{3}{2}|b| < -|y_n| < -\frac{|b|}{2}\\
\Longleftrightarrow~&\frac{|b|}{2} < |y_n| < \frac{3}{2}|b|
\end{align*}
\]

つまり\(b\geq 0\)，\(b<0\)に関わらず\(\frac{|b|}{2} < |y_n| < \frac{3}{2}|b|\)が成り立つ．整理すると，
\[\forall \epsilon <\frac{|b|}{2}\exists N’\left[n>N’ \Longrightarrow \frac{|b|}{2} < |y_n| < \frac{3}{2}|b|\right]\tag{ウ}\]
が言えたことになる．この準備のもとで，改めて\((\ast)\)を示す．

（イ），（ウ）により，任意の\(\epsilon < \frac{|b|}{2}\)に対して，\(N’\)が存在し，\(n>N’\)をみたす\(n\)について，次の式が成り立つ：
\[\frac{|y_n-b|}{|b||y_n|}<\frac{\epsilon}{|b|\cdot \frac{|b|}{2}}=\frac{2\epsilon}{|b|^2}\]

すなわち
\[\forall \epsilon<\frac{|b|}{2} \exists N’ \left[n>N’ \Longrightarrow \left|\frac{1}{y_n}-\frac{1}{b}\right|<\frac{2\epsilon}{|b|^2}\right]\]
したがって
\[\lim_{n\rightarrow \infty}\frac{1}{y_n}=\frac{1}{b}\]

（証明終）

投稿日:

定積分の再定義

（高校生へ注意）この記事を読む際は，教科書の定積分の定義は忘れて読んで下さい．一旦無の状態に戻るのが理解のポイントです．

私たちは四角形の面積なら求められます．タテ\(\times\)ヨコ．さらにここから，三角形の面積やら台形の面積やらをも求められることになります．では，下のような曲線を含む図形Aの面積はどうやって求めればいいのでしょうか．というか，何を指して曲線を含む図形Aの「面積」とすればいいのでしょうか？

下図のような\(x\)軸，\(y=f(x)\)，\(x=a\)，\(x=b\)状況を仮定した上で，次のように考えてみます：

まず，図形を分割します．何個に分割してもいいのですが，ここでは\(n\)個に分割（等分でなくともよい）することにします．\[a=x_0<x_1<x_2<x_3<\cdots<x_{n-1}<x_{n}=b\]という分割です．

次に，これら\(n\)個の図形を，長方形に近似します．区間\([x_{i-1},~x_{i}]\)において「高さ」をとる\(x\)を\(\xi_i\)とします．区間\([x_{i-1},~x_{i}]\)上のどの点\(x\)を\(\xi_i\)とするかは任意です（ちなみに\(\xi\)はギリシャ文字で「グザイ」「クシー」などと読みます）．

これらの長方形の面積を求めます．例えば左から\(i\)番目の長方形の面積なら，横幅は\(x_{i}-x_{i-1}\)です．高さは\(f(\xi_i)\)です．したがって左から\(i\)番目の長方形の面積は
\[f(\xi_i)(x_{i+1}-x_i)\]
と書けます．さらに，\(x_{i+1}-x_i=\Delta x_i\)とおけば，
\[f(\xi_i)\Delta x_i\]
と書けます．これを\(n\)個寄せ集めるのですから，敷き詰めた長方形の面積の和は
\[\sum^{n}_{i=0}f(\xi_i)\Delta x_i\]
と表されることになります．これをリーマン和と呼びます．

この「リーマン和」をもってして図形Aの「面積」とするのはどうでしょうか？…それはちょっとマズイ気がします．なぜなら，図形Aとリーマン和とではスキマ（誤差）が大きすぎますから（下図参照）．

どうすればスキマ（誤差）は小さくなるでしょうか？各長方形の幅を小さくすれば，細長い長方形になって，スキマは小さくなります．当然，スキマは小さければ小さいほど，今私たちにとって欲しいものが正確に求まりそうな気がします．各長方形の幅を小さくするには，\(n\)を大きく，すなわち分割の数を大きくしてやればいいでしょう．


式で表すと，
\[\lim_{n\rightarrow \infty}\sum^{n}_{i=0}f(\xi_i)\Delta x_i\]
これなら，図形の「面積」と呼んでも差し支えなさそうです．そこで，この極限値を図形Ａの「面積」と定義し，「定積分」と名付け，記号\[\int^b_a f(x)dx\]で表すことにします．

定積分の定義\[\int^b_a f(x)dx:=\lim_{n\rightarrow \infty}\sum^{n}_{i=0}f(\xi_i)\Delta x_i\]

\(:=\)は「左辺を右辺で定義する」という意味です．

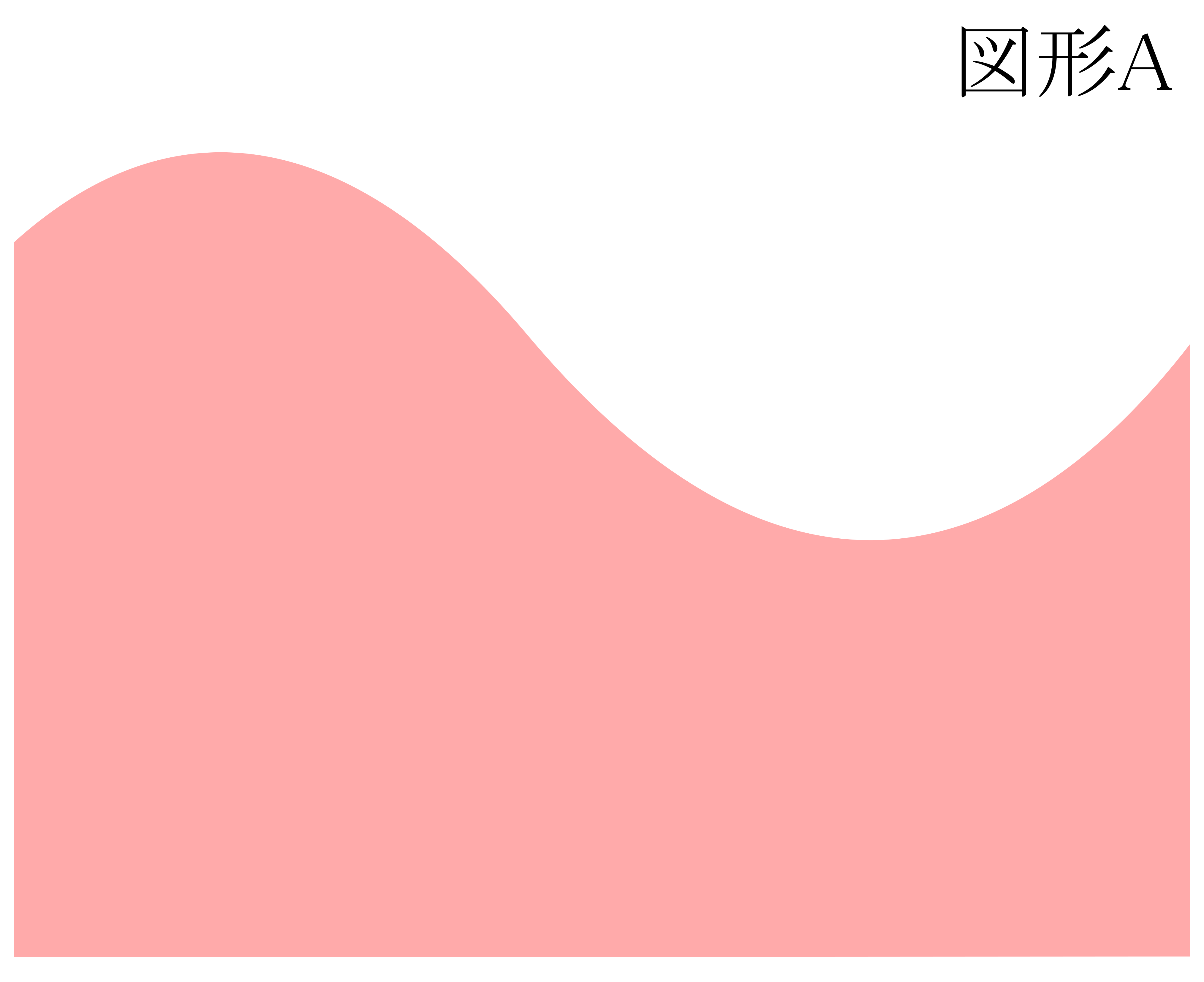
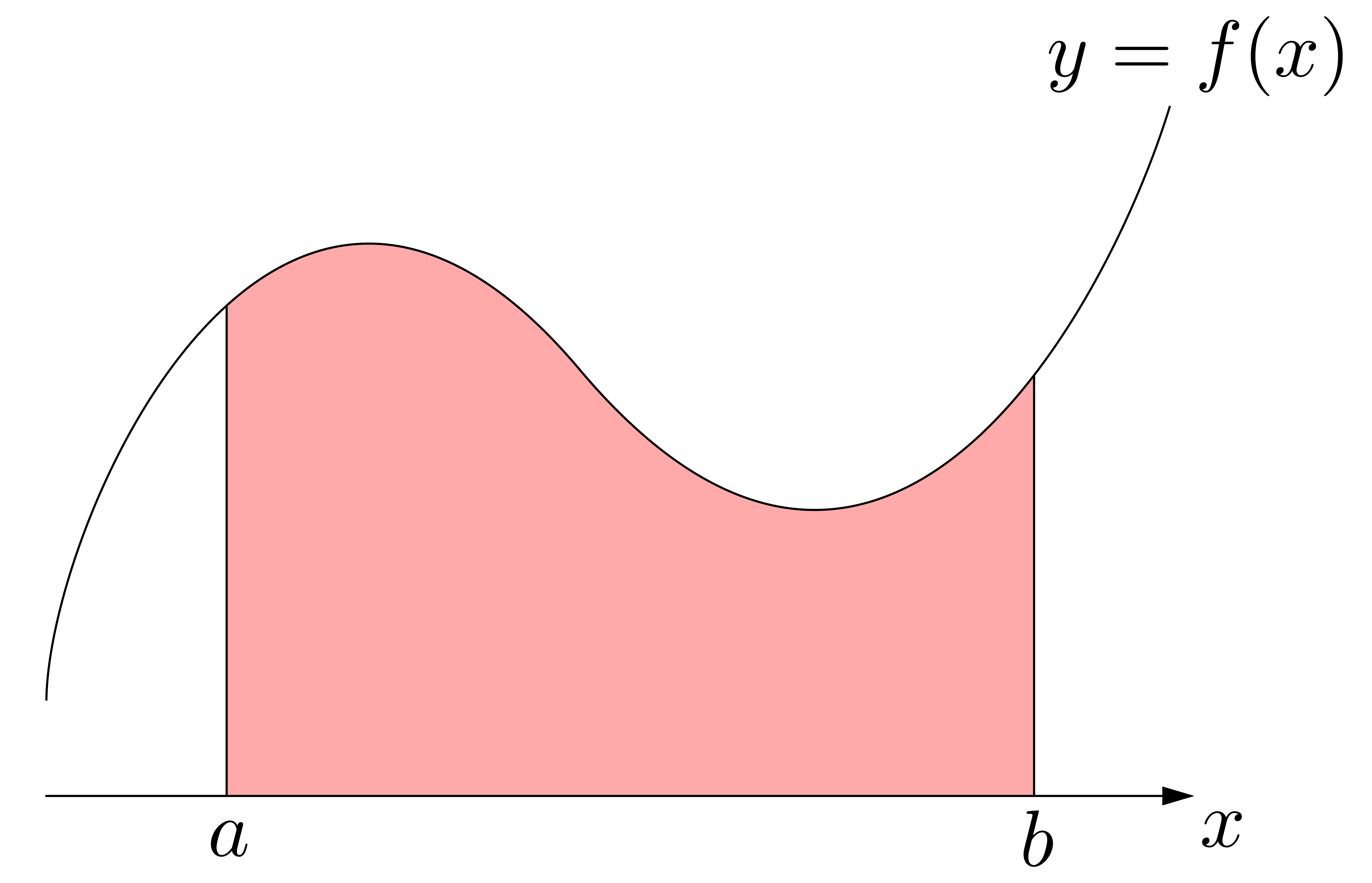
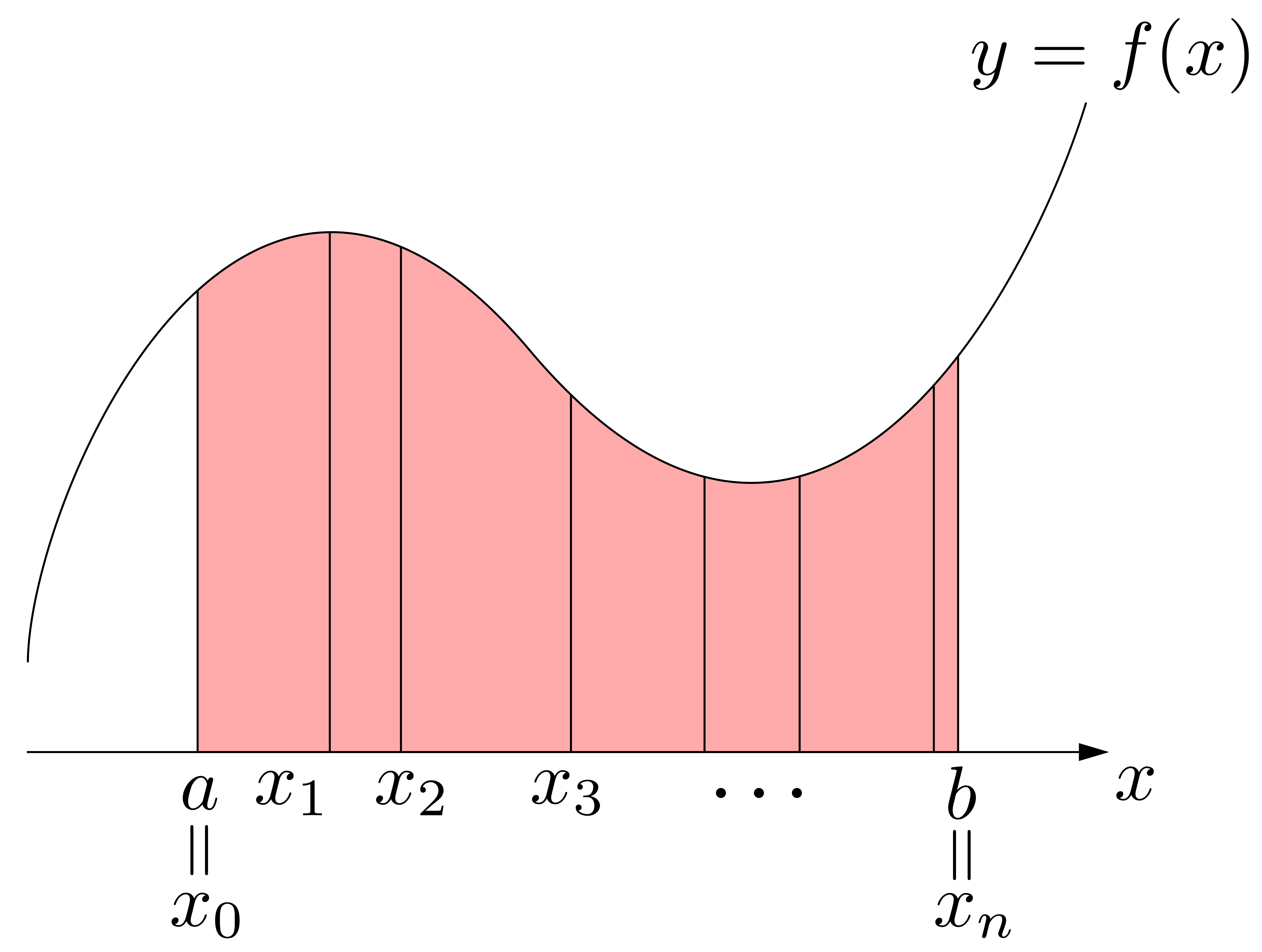
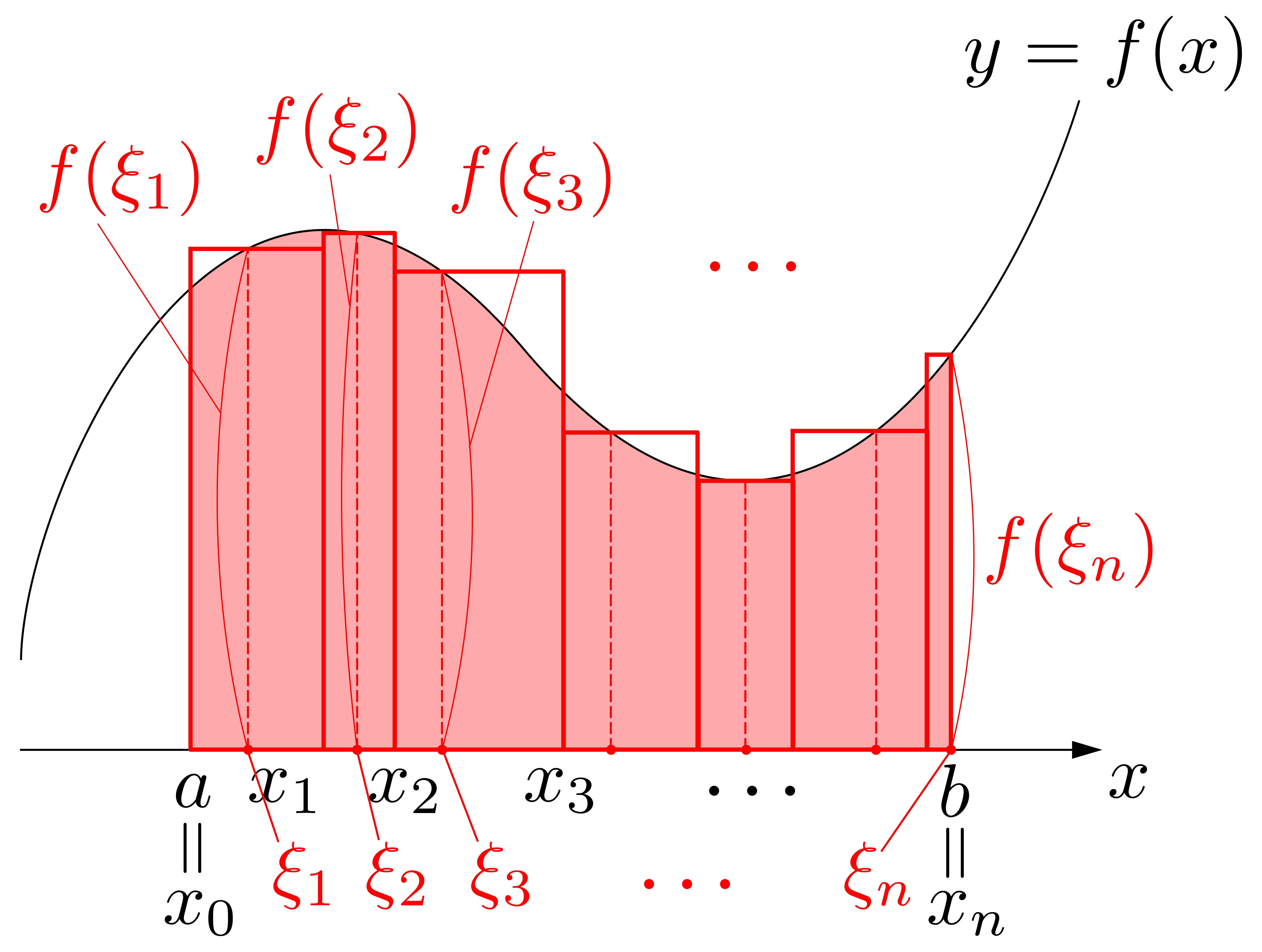
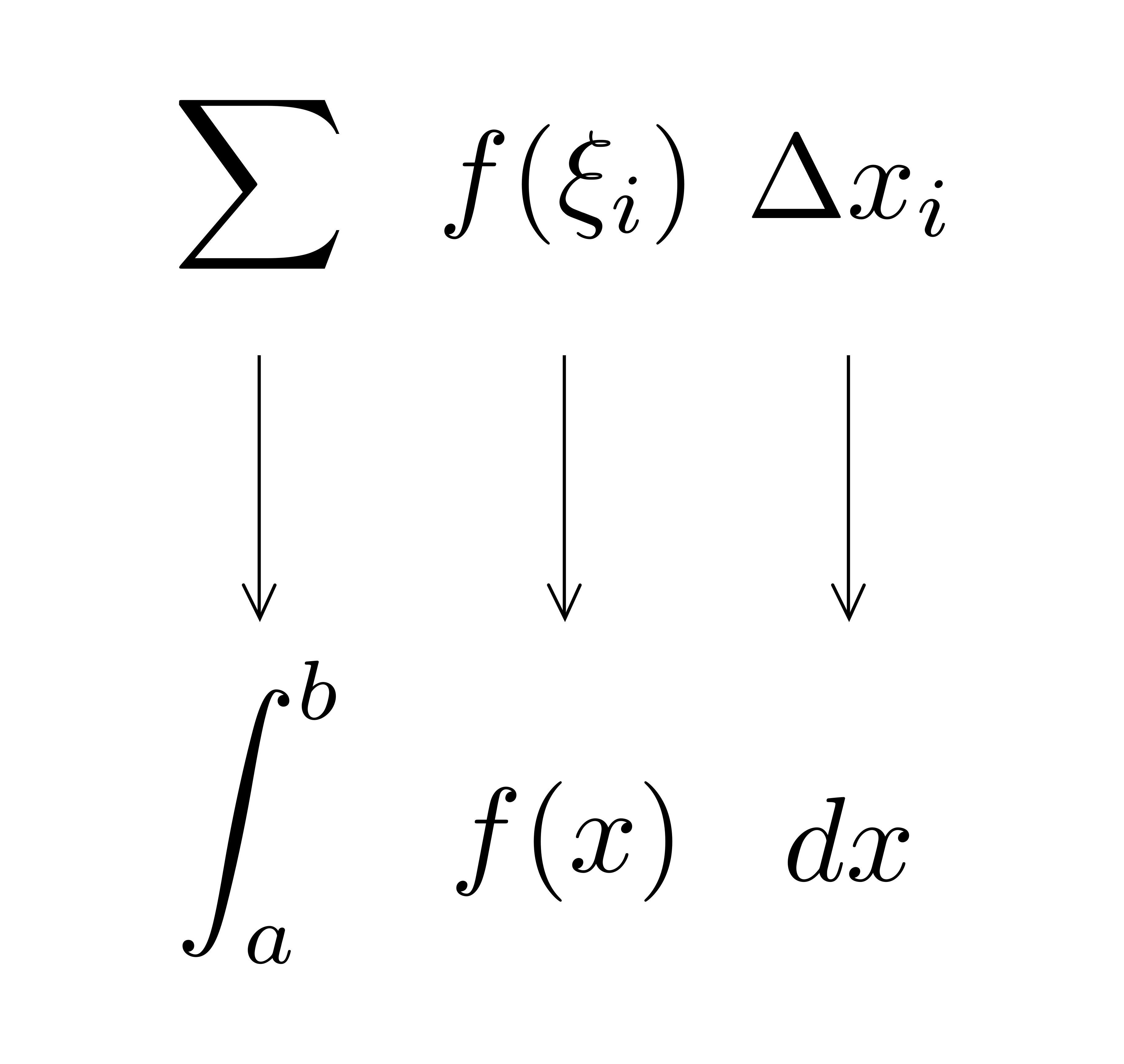以上を見ると，\(\displaystyle \int^b_a f(x)dx\)の\(\displaystyle \int\)や\(dx\)の「イメージ」が見えてきます．右図に示すように，\(\displaystyle \sum\)が\(\displaystyle \int\)に，\(\Delta x_i\)が\(dx\)と対応しているわけです．

 

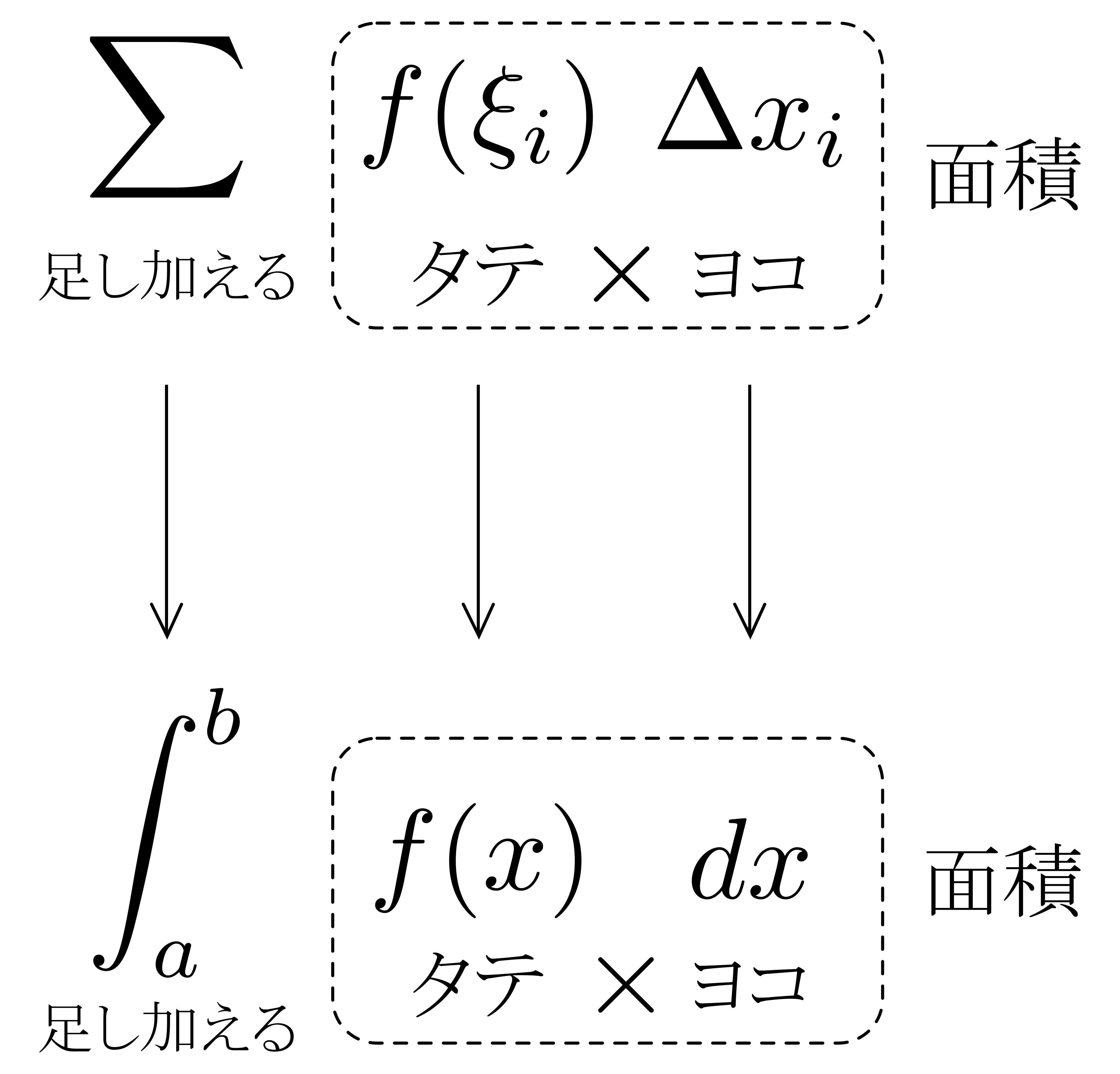ここで，\(\displaystyle \sum\ f(\xi_i)\Delta x_i\)の意味を思い出しましょう．\(f(\xi_i)\)が「タテ」，\(\Delta x_i\)が「ヨコ」を表すのでしたから，\(f(\xi_i)\times\Delta x_i\)は「長方形の面積」を意味し，その長方形の面積\(f(\xi_i)\Delta x_i\)を\(\displaystyle \sum\)する（足し加える），という意味でした．

以上を踏まえて\(\displaystyle \int^b_a f(x)dx\)を眺めると，これは「微小面積\(f(x)\times dx\)を\(\displaystyle \int\)したもの（連続的に足し加えたもの）」と読み取れることが分かります！

定積分を「リーマン和の極限」とみなす捉え方は，とても自然で，記号の導入も全く違和感がありません．さらに，右図に示した記号の解釈は，定積分の問題を扱う上で極めて重要な解釈になります．

次回はこの定積分の定義に従って図形の面積を計算してみます．すると，大きな問題に直面します…．

投稿日:

★解析学演習

すべての\(n\)で\(x_n>p\)，かつ\(\displaystyle \lim_{n\rightarrow \infty}x_n=a\)ならば\(a\geq p\)であることを証明せよ．
（田島一郎 解析入門 P10問3(2)）

（証明）

背理法で示す．与えられた命題は
\[\left(\forall n[x_n>p]\land \lim_{n\rightarrow \infty}x_n=a \right)\Longrightarrow a \geq p\]
である．この命題の否定をとると
\[\overline{\left(\forall n[x_n>p]\land \lim_{n\rightarrow \infty}x_n=a \right)\Longrightarrow a \geq p}\]
であるから，
\[
\begin{align*}
&\overline{\left(\forall n[x_n>p]\land \lim_{n\rightarrow \infty}x_n=a \right)\Longrightarrow a \geq p}\\
\Longleftrightarrow~&\overline{\overline{\forall n[x_n>p]\land \lim_{n\rightarrow \infty}x_n=a} \lor a \geq p}\\
\Longleftrightarrow~&\forall n[x_n>p]\land \lim_{n\rightarrow \infty}x_n=a \land a < p\\ \Longleftrightarrow~&\forall n[x_n>p]\land \left(\forall \epsilon>0 \exists N\big[n>N \Longrightarrow |x_n-a|<\epsilon\big]\right) \land a < p\\
\end{align*}
\]

\(a<p\)より\(p-a>0\)だから，\(\epsilon=p-a\)ととると，\(n>N\)をみたす\(n\)に対して
\[|x_n-a|<p-a\]
すなわち
\[
\begin{align*}
|x_n-a|<p-a~\Longleftrightarrow~&a-(p-a)< x_n <a+(p-a)\\
\Longleftrightarrow~&2a-p< x_n < p
\end{align*}
\]
が成り立つが，これは\[\forall n[x_n>p]\]に反する．（証明終）

投稿日:

★上に有界で単調増加な数列は収束する

上に有界で単調増加な数列\[a_1\leq a_2 \leq a_3 \leq \cdots \leq a_n\leq \cdots\]は収束する．

証明

上に有界であるから，上界が存在し，したがって上限（最小の上界）が存在する（なぜ？）．この上限を\(c\)とおき，この\(c\)に収束することを以下に示す．

任意の\(\epsilon>0\)に対して，\(c-\epsilon\)を考える．今，\(c\)が上限，すなわち最小の上界であるから，\(c-\epsilon\)はもはや上界ではない．したがって，\(c-\epsilon\)より大きく\(c\)以下の項（☆）が存在する．
\[a_1\leq a_2 \leq a_3 \leq \cdots \leq a_n \leq \cdots \leq c-\epsilon < \text{（☆）} \leq c\]
（☆）の項たちを
\[a_N \leq a_{N+1} \leq a_{N+2} \leq \cdots\]
とおく．すると，
\[c-\epsilon < a_N \leq a_{N+1} \leq a_{N+2} \leq \cdots \leq c < c+\epsilon \]
すなわち，\(N\)以上の\(i\)について
\[|a_{i}-c|<\epsilon\] が成り立つ．また，この\(N\)は，\(\epsilon\)に応じて定まる（存在する）ので，結局 \[\forall \epsilon>0 \exists N \big[i > N \Longrightarrow |a_{i}-c|<\epsilon\big]\]
と言える．したがって
\[\lim_{n\rightarrow \infty}a_n=c\]
よって数列\(\{a_n\}\)は収束する．（証明終）

投稿日:

否定をとることの難しさと論理式の有用性

背理法で示す方針の場合，与えられた命題を否定する必要がありますが，これが意外と難しいケースがあります．

\(xy\)平面内の相異なる４点\(P_1,~P_2,~P_3,~P_4\)とベクトル\(\overrightarrow{v}\)に対し，\(k\neq m\)のとき\(\overrightarrow{P_kP_m}\cdot \overrightarrow{v}\neq 0\)が成り立っているとする．このとき，\(k\)と異なるすべての\(m\)に対し\[\overrightarrow{P_kP_m}\cdot\overrightarrow{v}<0\]が成り立つような点\(P_k\)が存在することを示せ．（京都大・文）

この問題の場合，与えられた命題は

「\(k\neq m\)のとき\(\overrightarrow{P_kP_m}\cdot \overrightarrow{v}\neq 0\)が成り立っているとする．このとき，\(k\)と異なるすべての\(m\)に対し\(\overrightarrow{P_kP_m}\cdot\overrightarrow{v}<0\)が成り立つような点\(P_k\)が存在する」

です．この否定をとればいいわけですが，どこからどう手をつければいいのかいまいちわからない，できたとしてもなんだか不安…．そこで，ここでは論理記号を用いて捉えてみます．与えられた命題を次の４つの部分に分けて翻訳していきます．

      1. \(k\neq m\)のとき\(\overrightarrow{P_kP_m}\cdot \overrightarrow{v}\neq 0\)が成り立っているとする．
      2. このとき，
      3. \(k\)と異なるすべての\(m\)に対し\(\overrightarrow{P_kP_m}\cdot\overrightarrow{v}<0\)が成り立つ
      4. ような点\(P_k\)が存在する

１．「\(k\neq m\)のとき\(\overrightarrow{P_kP_m}\cdot \overrightarrow{v}\neq 0\)が成り立っているとする」は
\[k\neq m \Longrightarrow \overrightarrow{P_kP_m}\cdot \overrightarrow{v}\neq 0\]

２．「このとき」は\[\Longrightarrow\]

３．「\(k\)と異なるすべての\(m\)に対し\(\overrightarrow{P_kP_m}\cdot\overrightarrow{v}<0\)が成り立つ」は\[\forall m \big[m\neq k \Longrightarrow \overrightarrow{P_kP_m}\cdot\overrightarrow{v}<0\big]\]

４．「ような点\(P_k\)が存在する」は
\[\exists P_k\]

ですから，以上を繋げると，
\[\big(k\neq m \Longrightarrow \overrightarrow{P_kP_m}\cdot \overrightarrow{v}\neq 0\big)\Longrightarrow\exists P_k\forall m \big[m\neq k \Longrightarrow \overrightarrow{P_kP_m}\cdot\overrightarrow{v}<0\big]\]
となります．これの否定を考えます．
\[\overline{\big(k\neq m \Longrightarrow \overrightarrow{P_kP_m}\cdot \overrightarrow{v}\neq 0\big)\Longrightarrow\exists P_k\forall m \big[m\neq k \Longrightarrow \overrightarrow{P_kP_m}\cdot\overrightarrow{v}<0\big]}\]

ここで，一般に
\[
\begin{align*}
&(A\rightarrow B)\Longleftrightarrow \overline{A}\lor B
\end{align*}
\]
ですから，
\[\overline{A\rightarrow B}\Longleftrightarrow \overline{\overline{A} \lor B}\Longleftrightarrow A \land \overline{B}\]
です．したがって，
\[
\begin{align*}
&\overline{\big(k\neq m \Longrightarrow \overrightarrow{P_kP_m}\cdot \overrightarrow{v}\neq 0\big)\Longrightarrow\exists P_k\forall m \big[m\neq k \Longrightarrow \overrightarrow{P_kP_m}\cdot\overrightarrow{v}<0\big]}\\
\Longleftrightarrow~&\big(k\neq m \Longrightarrow \overrightarrow{P_kP_m}\cdot \overrightarrow{v}\neq 0\big)\land \overline{\exists P_k\forall m \big[m\neq k \Longrightarrow \overrightarrow{P_kP_m}\cdot\overrightarrow{v}<0\big]}\\
\Longleftrightarrow~&\big(k\neq m \Longrightarrow \overrightarrow{P_kP_m}\cdot \overrightarrow{v}\neq 0\big)\land \forall P_k\exists m \big[\overline{m\neq k \Longrightarrow \overrightarrow{P_kP_m}\cdot\overrightarrow{v}<0}\big]\\
\Longleftrightarrow~&\big(k\neq m \Longrightarrow \overrightarrow{P_kP_m}\cdot \overrightarrow{v}\neq 0\big)\land \forall P_k\exists m \big[m\neq k \land \overline{\overrightarrow{P_kP_m}\cdot\overrightarrow{v}<0}\big]\\ \Longleftrightarrow~&\big(k\neq m \Longrightarrow \overrightarrow{P_kP_m}\cdot \overrightarrow{v}\neq 0\big)\land \forall P_k\exists m \big[m\neq k \land \overrightarrow{P_kP_m}\cdot\overrightarrow{v}\geq0\big]\\ \Longleftrightarrow~&\big(k\neq m \Longrightarrow \overrightarrow{P_kP_m}\cdot \overrightarrow{v}\neq 0\big)\land \forall P_k\exists m \big[(m\neq k \land \overrightarrow{P_kP_m}\cdot\overrightarrow{v}>0)\lor(m\neq k \land\overrightarrow{P_kP_m}\cdot\overrightarrow{v}=0)\big]\\
\Longleftrightarrow~&\big(k\neq m \Longrightarrow \overrightarrow{P_kP_m}\cdot \overrightarrow{v}\neq 0\big)\land \forall P_k\big[\exists m(m\neq k \land \overrightarrow{P_kP_m}\cdot\overrightarrow{v}>0)\lor\exists m(m\neq k \land\overrightarrow{P_kP_m}\cdot\overrightarrow{v}=0)\big]\\
\Longleftrightarrow~&\big(k\neq m \Longrightarrow \overrightarrow{P_kP_m}\cdot \overrightarrow{v}\neq 0\big)\land \forall P_k\exists m(m\neq k \land \overrightarrow{P_kP_m}\cdot\overrightarrow{v}>0)
\end{align*}
\]
となります．

もとの問題の解説では他の解法があったのですが，別解としての上記のように否定をとり矛盾を示す方針が載っていました．が，その「否定をとる」という作業の時点で既に難しく，ならば論理式で記述したらどうなるかなと思い考えてみました．見た目こそ厳ついものの，論理式の扱いに慣れさえすればとても分かりやすく明解です．

投稿日:

原因の確率

教科書では「研究」「発展」などに分類され，端っこの方に追いやれている話題です．授業でも扱わないことが多いので，無視して先に進む人も多いと思いますが，これは実はとても面白い話題です．今回はこの話題について触れてみます．

Ａさんはがん検査を受けた．その結果は「要精密検査」であった．この検査は，実際にがんの人が要精密検査とされる確率が\(90\%\)で，実際にはがんではないのに要精密検査とされる確率が\(10\%\)であるような検査である．検診を受ける人の１０００人に１人は実際にがんにかかっているとすると，Ａさんが実際にがんである確率はいくらか．

Ａさんを自分に置き換えて考えてみましょう．検査を受けたら「要精密検査」で，実際にがんの人が要精密検査とされる確率が\(90\%\)と言われたら，「ああ自分はがんなんだ…」と考え落ち込むのではないでしょうか．が，落ち着むのは尚早です．今置かれた状況をよく見ると「『要精密検査』という結果が与えられたときの，実際にがんである確率」ですから，これは条件付き確率です．では，実際に計算して自分ががんである確率を求めてみましょう！（注意：条件付き確率とベイズの定理についての知識が必要になります．未習の人はこれらの記事を先に読んでみてください．）条件付き確率の定義より，

\[P(\text{実際にがん}|\text{要精密検査})=\frac{P(\text{実際にがん}\cap\text{要精密検査})}{P(\text{要精密検査})}\]

まず，分子から求めてみます．確率の乗法定理より，
\[P(\text{実際にがん}\cap\text{要精密検査})=P(\text{実際にがん})P(\text{要精密検査}|\text{実際にがん})\]
です．問題文より，
\[P(\text{実際にがん})=\frac{1}{1000},\quad P(\text{要精密検査}|\text{実際にがん})=\frac{90}{100}\]
です．ですから分子は\[\frac{1}{1000}\times\frac{90}{100}\]となります．

次に分母．\(P(\text{要精密検査})\)つまり「『要精密検査』とされる確率」です．「『要精密検査』とされる」という状況には２通りあります．すなわち，

          • 「実際にがんで，『要精密検査』」
          • 「実際にはがんではないのに，『要精密検査』」

という２通りの場合です．それぞれ

          • \(P(\text{実際にがん}\cap \text{要精密検査})\)
          • \(P(\text{実際はがんではない}\cap \text{要精密検査})\)

と表されますから，結局分母は\[P(\text{実際にがん}\cap \text{要精密検査})+P(\text{実際はがんではない}\cap \text{要精密検査})\]と表されます（全確率の定理）．さらに，確率の乗法定理より，この式は
\[P(\text{実際にがん})P(\text{要精密検査}|\text{実際にがん})+P(\text{実際はがんではない})P(\text{要精密検査}|\text{実際はがんではない})\]と表されます．前の項は前半で求めました．\(\frac{1}{1000}\times \frac{90}{100}\)．後ろの項は，問題文より，
\[P(\text{実際はがんではない})=\frac{999}{1000},\quad P(\text{要精密検査}|\text{実際はがんではない})=\frac{10}{100}\]ですから\(\frac{999}{1000}\times\frac{10}{100}\)．ですから分母は
\[\frac{1}{1000}\times \frac{90}{100}+\frac{999}{1000}\times\frac{10}{100}\]となります．したがって，求める確率\(P(\text{実際にがん}|\text{要精密検査})\)は，
\[
\begin{align*}
P(\text{実際にがん}|\text{要精密検査})&=\frac{\frac{1}{1000}\times\frac{90}{100}}{\frac{1}{1000}\times \frac{90}{100}+\frac{999}{1000}\times\frac{10}{100}}\\
&=\frac{1\times 90}{1\times 90 +999\times 10}\\
&=\frac{9}{9+999}\\
&=\frac{1}{112}\approx 0.00893
\end{align*}
\]となります．なんと，「要精密検査」と言われ実際にがんである確率はたったの\(0.00893\)，つまり\(1\%\)にも満たない，ということです！

このように，確率は時として人間の直感を大きく裏切ります．しかし，論理によってはじき出された結果である以上，人間の感情としてどう感じようとそれは受け入れざるを得ない．そこが数学の面白さ・頼もしさのひとつだと思います．

投稿日:

全確率の定理

Ａ君が友人とストリートファイターⅡ（スーファミ）で友人Ｂと対戦している．Ａ君が勝つ確率は？

という問題があったとしましょう．こんな問題を見たらどう思いますか？（勝つか負けるか，２分の１だ！は間違いですよ～）当然，こう思うと思います「そらＡ君が誰使うかによるだろ」と．では，どんな場合があるでしょうか．リュウを使う場合，ケンを使う場合，ガイルを使う場合，春麗を使う場合…．いろいろ考えられます．そして，ストⅡは２人同時に操作はできません（そのラウンドで１人のプレイヤーがリュウとケンと同時に操作し味方２人状態で戦うことはできません！）．つまり同時に起こることはありませんから，これらの場合は互いに排反です．したがって，求める確率は
\[
\begin{align*}
P(\text{A君が勝つ})=&P(\text{A君が勝つ}\cap\text{リュウを使う})+P(\text{A君が勝つ}\cap\text{ケンを使う})\\
&+P(\text{A君が勝つ}\cap\text{エドモンド本田を使う})+P(\text{A君が勝つ}\cap\text{春麗を使う})\\
&+P(\text{A君が勝つ}\cap\text{ブランカを使う})+P(\text{A君が勝つ}\cap\text{ザンギエフを使う})\\
&+P(\text{A君が勝つ}\cap\text{ガイルを使う})+P(\text{A君が勝つ}\cap\text{ダルシムを使う})
\end{align*}
\]
「Ａ君が勝つ」という事象を\(A\)，「リュウを使う」という事象を\(B_1\)，「ケンを使う」という事象を\(B_2\)，「エドモンド本田を使う」という事象を\(B_3\)，・・・，「ダルシムを使う」という事象を\(B_8\)とおくことにすれば，上の式は
\[
\begin{align*}
P(A)=&P(A\cap B_1)+P(A\cap B_2)+P(A\cap B_3)+P(A\cap B_4)\\
&+P(A\cap B_5)+P(A\cap B_6)+P(A\cap B_7)+P(A\cap B_8)\\
&=\displaystyle \sum^{8}_{i=1}P(A\cap B_i)
\end{align*}
\]すなわち\[P(A)=\displaystyle \sum^{8}_{i=1}P(A\cap B_i)\]と書けることがわかります．これを一般化すると，

全確率の定理\[P(A)=\displaystyle \sum^{\infty}_{i=1}P(A\cap B_i)\]

であると言えそうです．これを全確率の定理と呼びます．

ところで「ストリートファイター」ってゲーム自体今はどれくらい知名度あるんだろう？僕の時代は知らない人はいないくらいに流行っていました（スクリューパイルドライバーが出せたらまさにヒーロー）．なので馴染みやすいかなと思って例に挙げましたが…．調べると今はストリートファイター５まであるみたいですね．プレイアブルキャラは４０人（！）らしいですから，この場合は\[P(A)=\displaystyle \sum^{40}_{i=1}P(A\cap B_i)\]ですね＾＾；

投稿日:

確率の乗法定理

条件付き確率の定義より，\[P(B|A)=\frac{P(B\cap A)}{P(A)}\]
両辺に\(P(A)\)を掛けることによって，\[P(A \cap B)=P(A)P(B|A)\]が得られます．（\(P(B \cap A)=P(A\cap B)\)としました）これを確率の乗法定理といいます．

確率の乗法定理（その１）\[P(A \cap B)=P(A)P(B|A)\]

日本語に翻訳すると「事象\(A\)と事象\(B\)が同時に起こる確率は，事象\(A\)の確率と，事象\(A\)の影響を受けた事象\(B\)の確率（条件付き確率）との積に等しい」ということで，少し確率の問題に慣れた人であればいつも無意識にやっている計算だと思います．例題で確認してみます．
当たりくじ３本を含む１０本のくじの中から，引いたくじはもとに戻さないで，１本ずつ２回続けてくじを引く．２本とも当たる確率を求めよ．また，２回目が当たる確率いくらか．

１回目が当たるという事象を\(A\)，２回目が当たるという事象を\(B\)とします．

（２本とも当たる確率）
求める確率は\(P(A\cap B)\)です．確率の乗法定理より，\(P(A \cap B)=P(A)P(B|A)\)ですから，\(P(A)\)と\(P(B|A)\)を求めましょう．\(P(A)=\frac{3}{10}\)なのは問題ないでしょう．\(P(B|A)\)を求めます．これは「１回目が当たったという事実のもとで２回目が当たる確率」ですから，「引いたくじはもとに戻さない（当たりが１枚減る）」ことに注意せねばなりません．１回目に当たりを引けば，その後全体の枚数は９枚，当たりは２枚になりますから，\(P(B|A)=\frac{2}{9}\)です．したがって求める確率は\[P(A \cap B)=P(A)P(B|A)=\frac{3}{10}\cdot\frac{2}{9}=\frac{1}{15}\]となります．

（２回目が当たる確率）
求める確率は\(P(B)\)です．まず気をつけて欲しいのは，求めようとしているのは確率\(P(B)\)であって確率\(P(B|A)\)ではない，ということ．すなわち，確率を求めようとしている今この時，まだ１回目は引いてもいない！何もしていない！ということです．まだなにもしていない，くじの前で黙って腕を組んだまま２回目を予想している（\(P(B)\)を求めようとしている）…そんなイメージです．１回目は引いてもいないし眼中にもありません．２回目だけを見つめています．以上に留意して，実際に\(P(B)\)を求めてみましょう．確率の定義に従います．２回目に起こりうるすべての場合の数は？２回目において，１０枚のくじのどれが引きやすくどれが引きにくいなどということはありません（同様に確からしい）．よって１０通り．題意に適する場合の数は？当たり３枚のうちどれが引きやすくどれが引きにくいということはやはりありません．よって３通り．したがって求める確率は，\[P(B)=\frac{3}{10}\]となります．\(P(B|A)\neq P(B)\)であることに注目してください．

次の問題です．

当たりくじ３本を含む１０本のくじの中から，１本ずつ２回続けてくじを引く．２本とも当たる確率を求めよ．ただし，引いたくじはもとに戻すものとする．また，２回目に当たる確率はいくらか．

（２本とも当たる確率）
求める確率は\(P(A\cap B)\)です．確率の乗法定理より，\(P(A \cap B)=P(A)P(B|A)\)ですから，\(P(A)\)と\(P(B|A)\)を求めましょう．\(P(A)=\frac{3}{10}\)なのは問題ないでしょう．\(P(B|A)\)を求めます．これは「１回目が当たったという事実のもとで２回目が当たる確率」なわけですが，今回は引いたくじをもとに戻しています．ですから，２回目の状況は１回目の状況となんら変化がないことになります．したがって，\(P(B|A)=\frac{3}{10}\)となります．よって，求める確率は\[P(A \cap B)=P(A)P(B|A)=\frac{3}{10}\cdot\frac{3}{10}=\frac{9}{100}\]となります．

（２回目が当たる確率）
求める確率は\(P(B)\)です．前問同様に考えます．２回目に起こりうるすべての場合の数は？２回目において１０枚のくじのどれもが同様に確からしい．よって１０通り．題意に適する場合の数は？当たり３枚のうちどれもがやはり同様に確からしい．よって３通り．したがって求める確率は，\[P(B)=\frac{3}{10}\]となります．前問と全く同じです．

さて，今回は\(P(B|A)\)，\(P(B)\)はどちらも\(\frac{3}{10}\)ですから\(P(B|A)=P(B)\)です．この，\[P(B|A)=P(B)\]が成り立つとき，事象\(A\)と事象\(B\)は独立であるといいます．この式を「翻訳」すると，「\(B\)の確率は\(A\)が起きたかどうかなんて関係ない」と，すなわち「事象\(A\)と事象\(B\)が互いに影響を及ぼしていない」と読み取ることができます．

以上の準備のもと，次の定理が成り立ちます．

確率の乗法定理（その２）事象\(A\)と事象\(B\)が独立，すなわち\(P(B|A)=P(B)\)のとき\[P(A \cap B)=P(A)P(B)\]

高校教科書では上の話を，「２つの試行同士が互いに影響を与えない」ことを「独立」であると定義し，そのもとで確率の乗法定理（その２）を紹介しています．そしてこの話とは別の話題として（大分後になってから）「条件付き確率」から「確率の乗法定理（その２）」を導く，という順序で説明しています．なので，確率の乗法定理が２回（しかもそのあいだかなり間を挟んでから）登場することになり，それらにどのような関係があるのかがいまいち見えづらいのではないでしょうか．

しかし，上でみたように\[\text{条件付き確率の定義}\rightarrow\text{確率の乗法定理その１}\rightarrow\text{「独立」の定義}\rightarrow\text{確率の乗法定理その２}\]という流れで理解すると，高校教科書では「別々のもの」として載っている２つの確率の乗法定理が同じもの（その１を特殊化したものがその２）であることが明解で，論理的にはしっくりくると個人的に思います．

もっとも，実用上においては（実際問題を解く上では）どちらの理解でも大差はないと思いますが…

© 2024 佐々木数学塾, All rights reserved.