数Ⅰの問題です。
まず,「~するときの範囲を求めよ」(「~するための条件を求めよ」)というのは「~するための必要十分条件を求めよ」と問うていると思われます。したがって「\(y=p(x-q)^2+q\)上のすべての点が放物線\(y=x^2-1\)の下側にあるような実数\(q\)が存在する」を同値変形することを考えます。日本語のままでは考えづらいので,この主張を論理記号を用いて表わしてみます。すると\[\exists q \in \mathbb{R} \forall x \in \mathbb{R}[x^2-1>p(x-q)^2+q]\]となります。したがって,
解答
\begin{align*}
&\exists q \in \mathbb{R} \forall x \in \mathbb{R}[x^2-1>p(x-q)^2+q]\\
\Longleftrightarrow~&\exists q \in \mathbb{R} \forall x \in \mathbb{R}[(1-p)x^2+2pqx-pq^2-q-1>0]\\
\Longleftrightarrow~&\exists q \in \mathbb{R} \forall x \in \mathbb{R} \begin{cases}(1-p)x^2+2pqx-pq^2-q-1>0 \\ 1-p>0 \lor 1-p=0 \lor 1-p < 0 \end{cases}\\
\Longleftrightarrow~&\exists q \in \mathbb{R} \forall x \in \mathbb{R}[((1-p)x^2+2pqx-pq^2-q-1>0\land p<1)\\
&\lor ((1-p)x^2+2pqx-pq^2-q-1>0\land p=1) \\
&\lor ((1-p)x^2+2pqx-pq^2-q-1>0\land p>1) ]\tag{1}
\end{align*}
ここで,\[\forall x\in \mathbb{R}[(1-p)x^2+2pqx-pq^2-q-1>0\land p=1]\]と\[\forall x\in \mathbb{R}[(1-p)x^2+2pqx-pq^2-q-1>0\land p>1]\]は偽の命題であるから,\((1)\)は
\[(1)\Longleftrightarrow~\exists q \in \mathbb{R} \forall x \in \mathbb{R}[(1-p)x^2+2pqx-pq^2-q-1>0\land p<1]\]とできる(※).したがって,
\begin{align*}
(1)\Longleftrightarrow~&\exists q \in \mathbb{R} \forall x \in \mathbb{R}[(1-p)x^2+2pqx-pq^2-q-1>0\land p<1]\\
\Longleftrightarrow~&\exists q \in \mathbb{R} [\forall x \in \mathbb{R}[(1-p)x^2+2pqx-pq^2-q-1>0]\land p<1]\\
\Longleftrightarrow~&\exists q \in \mathbb{R} [p^2q^2-(1-p)(-pq^2-q-1)<0\land p<1]\\
\Longleftrightarrow~&\exists q \in \mathbb{R} [p^2q^2-(1-p)(-pq^2-q-1)<0]\land p<1\\
\Longleftrightarrow~&\begin{cases}\exists q \in \mathbb{R} [pq^2+(1-p)q+1-p<0\land (p >0 \lor p < 0)]\\ p<1 \end{cases}\\
\Longleftrightarrow~&\begin{cases}\exists q \in \mathbb{R} [(pq^2+(1-p)q+1-p<0\land p >0) \lor (pq^2+(1-p)q+1-p<0\land p < 0)]\\ p<1 \end{cases} \\
\Longleftrightarrow~&\begin{cases}\exists q \in \mathbb{R}[pq^2+(1-p)q+1-p<0\land p >0] \lor \exists q \in \mathbb{R}[pq^2+(1-p)q+1-p<0\land p < 0]\\ p<1 \end{cases}\\
\Longleftrightarrow~&\begin{cases}(\exists q \in \mathbb{R}[pq^2+(1-p)q+1-p<0]\land p >0) \lor (\exists q \in \mathbb{R}[pq^2+(1-p)q+1-p<0]\land p < 0)\\ p<1 \end{cases}\\
\Longleftrightarrow~&\begin{cases}((1-p)^2-4p(1-p)>0 \land p>0)\lor p < 0\\ p<1 \end{cases}\\
\Longleftrightarrow~&\begin{cases}((p-1)(5p-1)>0 \land p>0)\lor p < 0\\ p<1 \end{cases}\\
\Longleftrightarrow~&\begin{cases}0 < p < \frac{1}{5}\lor p < 0\\ p<1 \end{cases}\\
\Longleftrightarrow~&0 < p < \frac{1}{5}\lor p < 0
\end{align*}
解答終
一般的な解答においてやっている(であろう)ことの正当性が個人的にいまいち納得できないので,論理式で考えてみました。一般的な解答において感じるその不安感というか気持ち悪さは,上の解答で行っている恒真命題の追加,分配法則,\(\forall\)や\(\exists\)の支配域の変更などがぼかされているためではないかと思います。さらに,この解答においても一つ気になるのが(※)の部分です。一般に,\[\forall x[p(x)\lor q(x)] \Longleftarrow \forall x p(x)\lor \forall x q(x)\]すなわち全称記号は\(\lor\)に関して分配は出来ませんから,そこだけちょっと誤魔化しています。これについては別記事で詳しく考えてみようと思います。


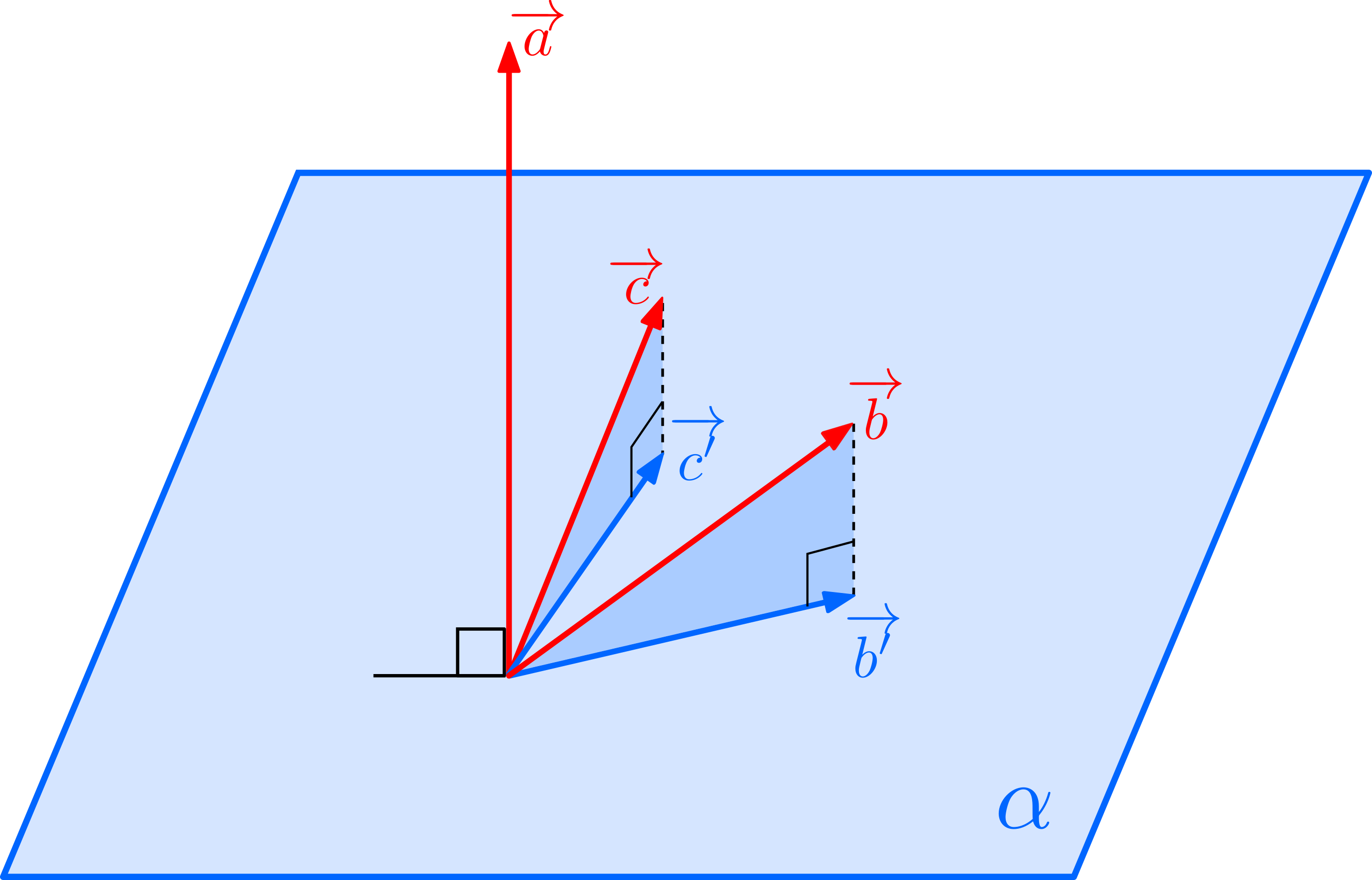
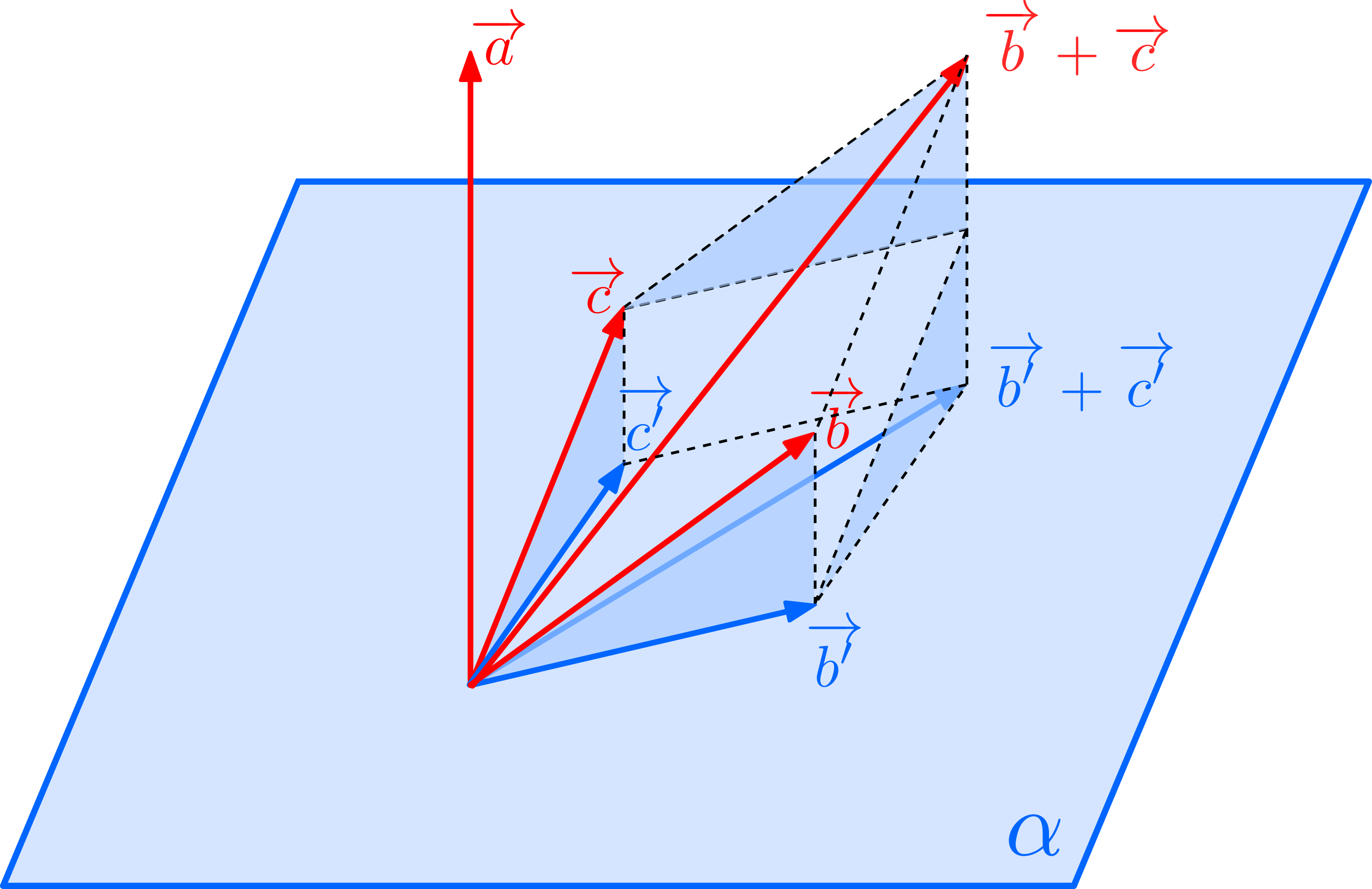
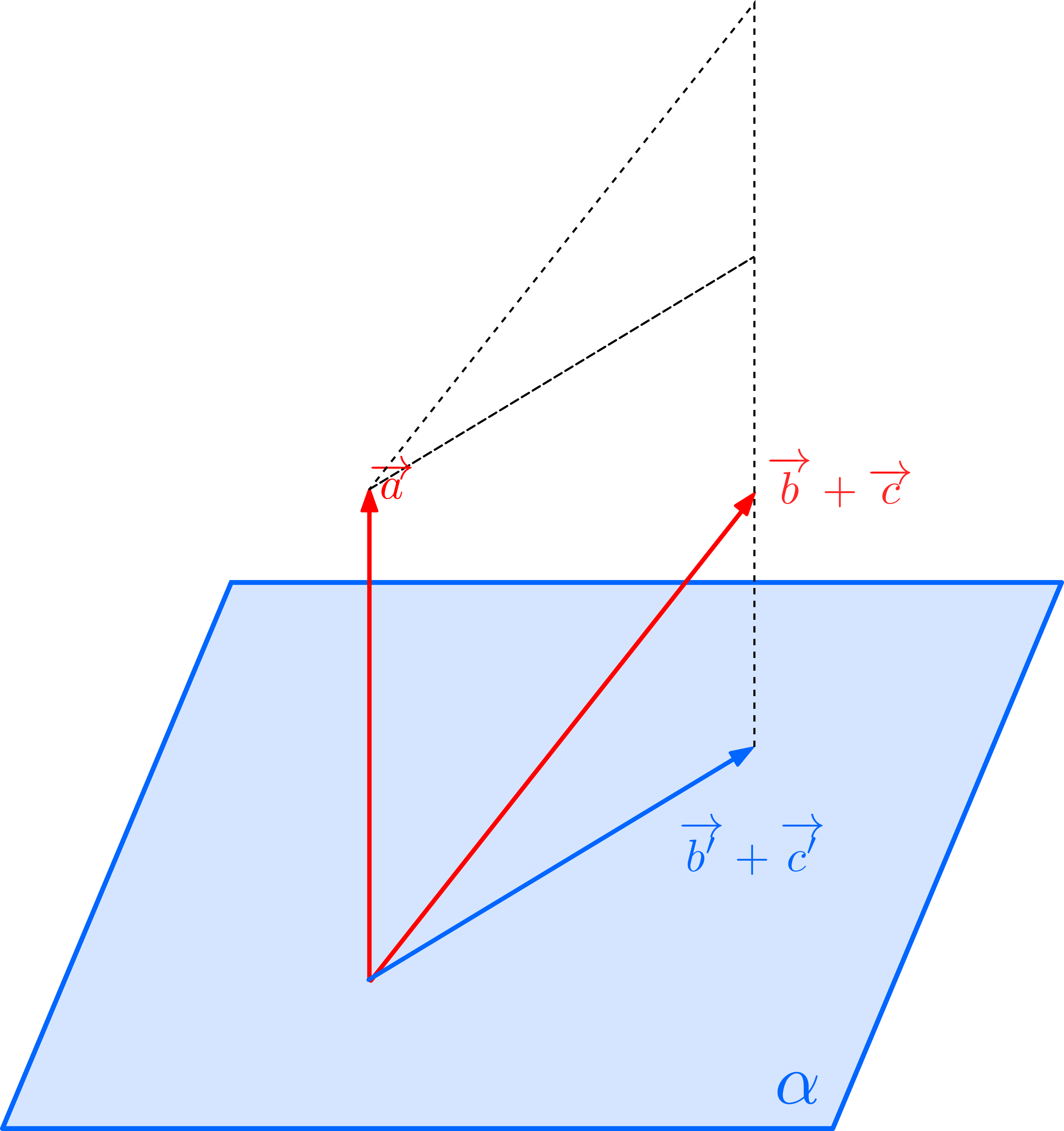 \((1)\)について:
\((1)\)について: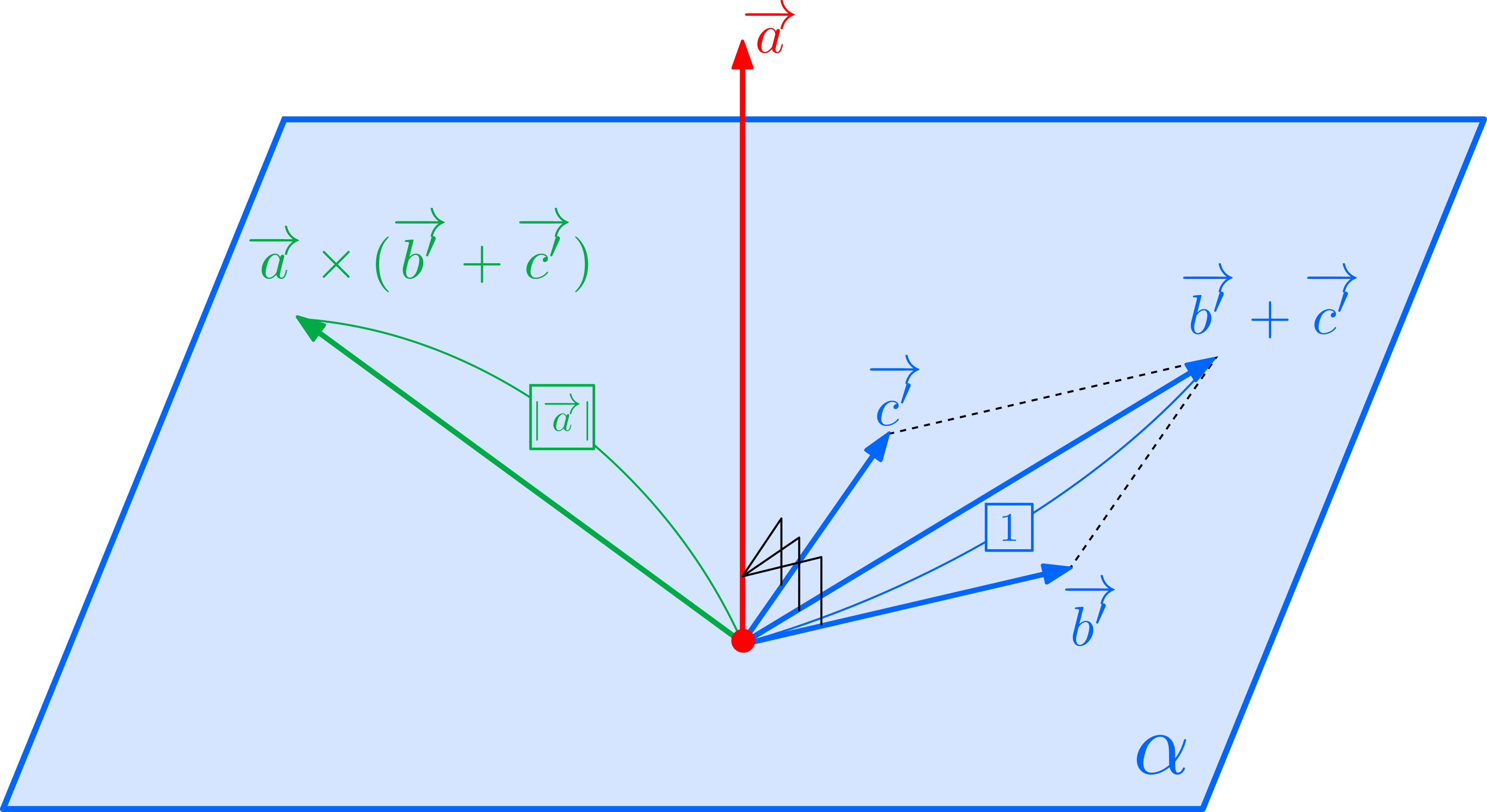
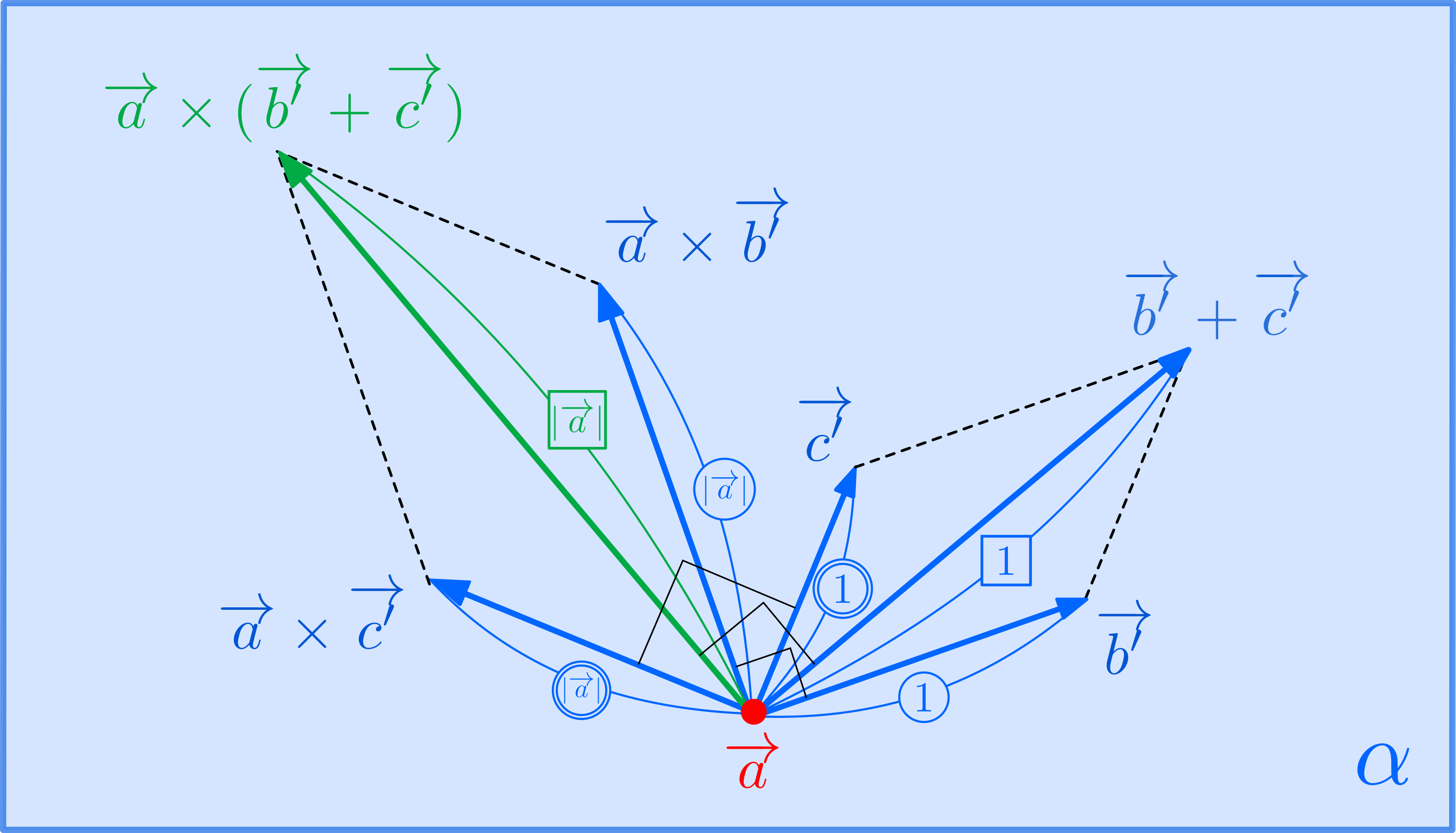
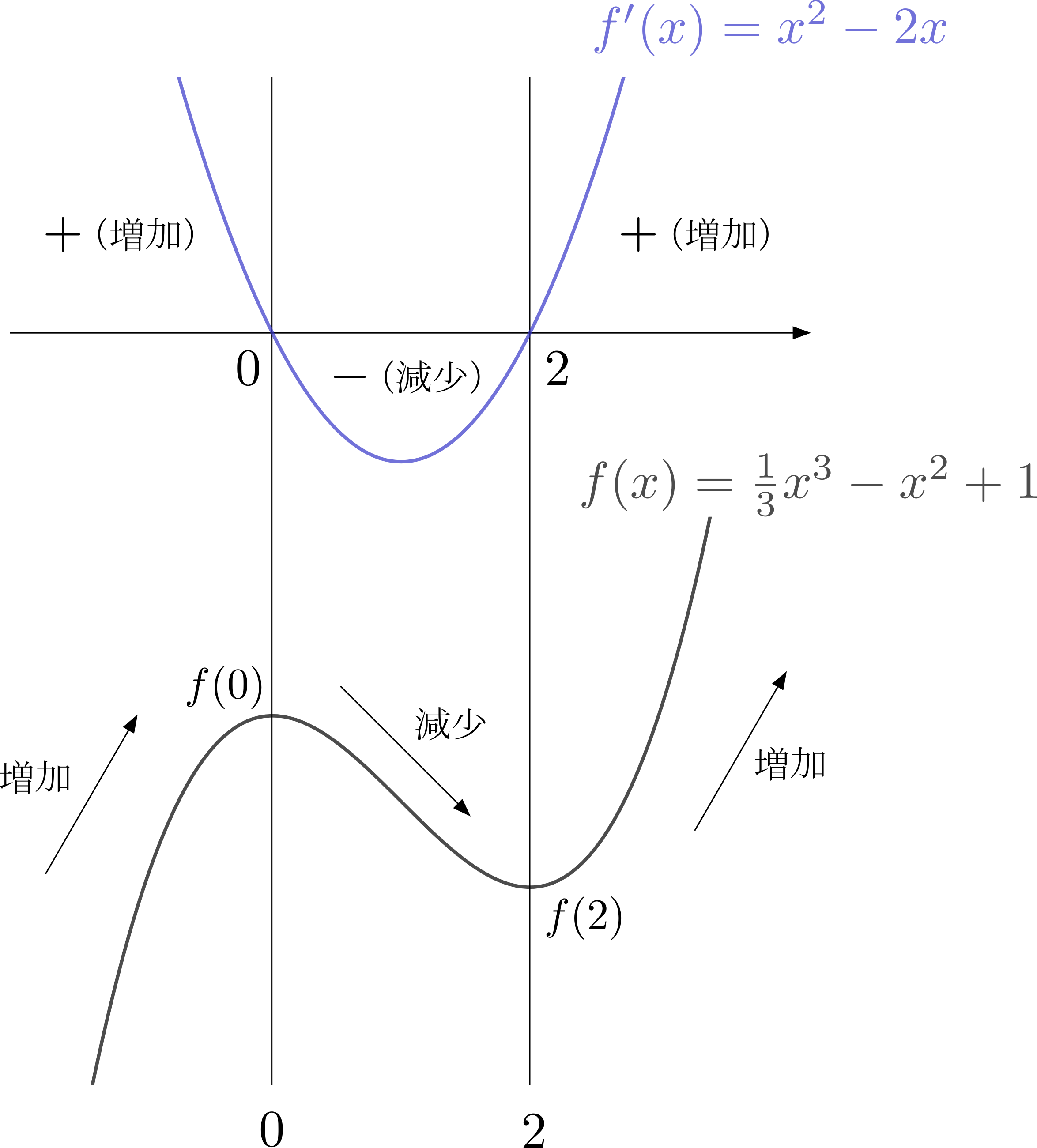
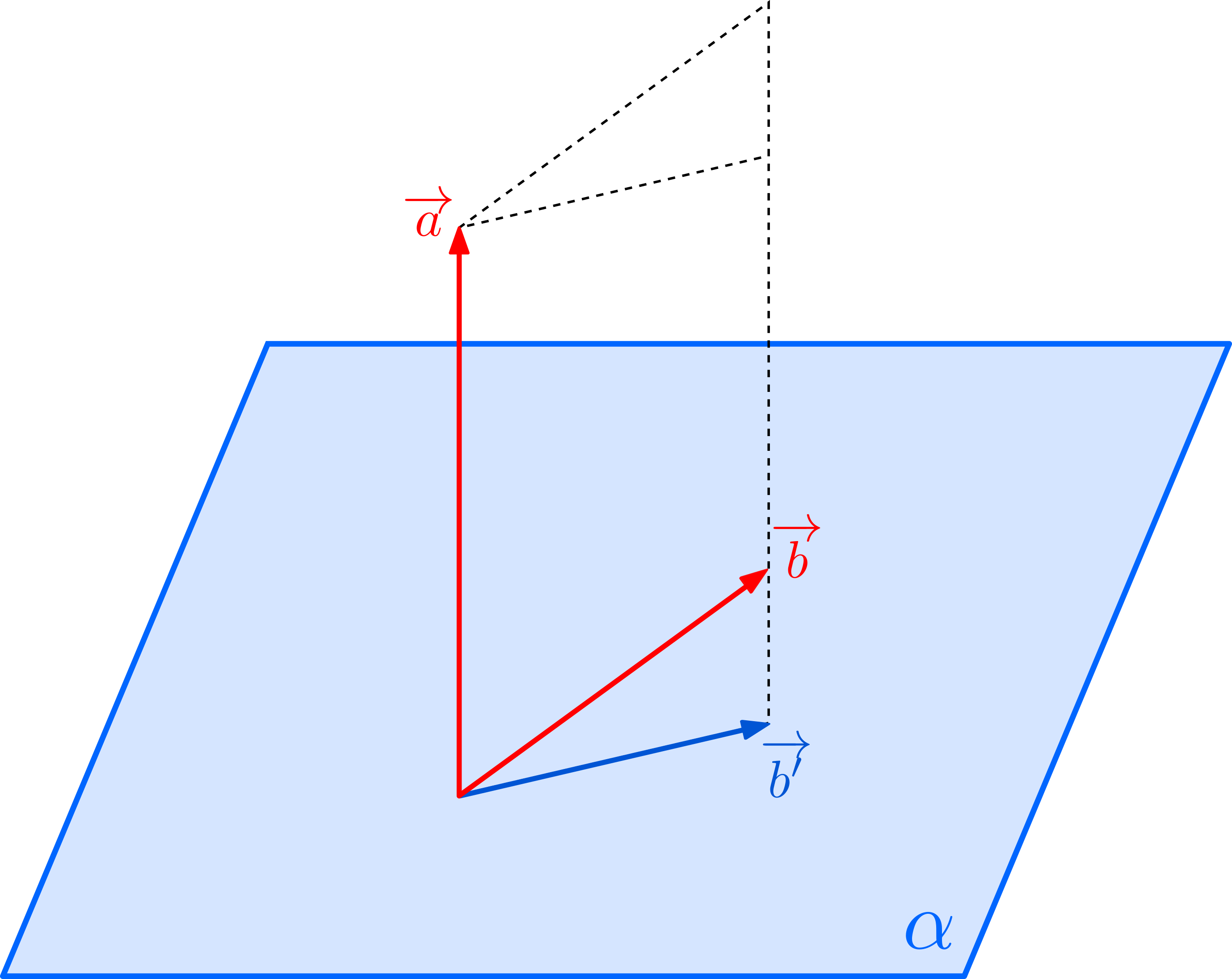 \((3)\)について:
\((3)\)について:
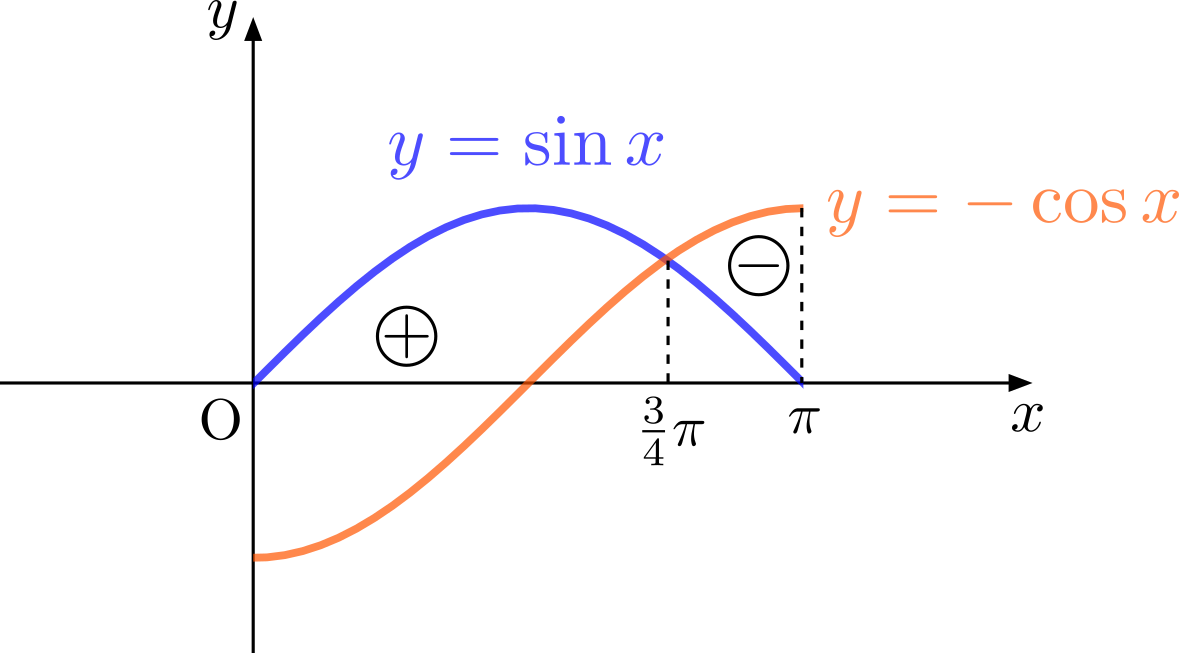


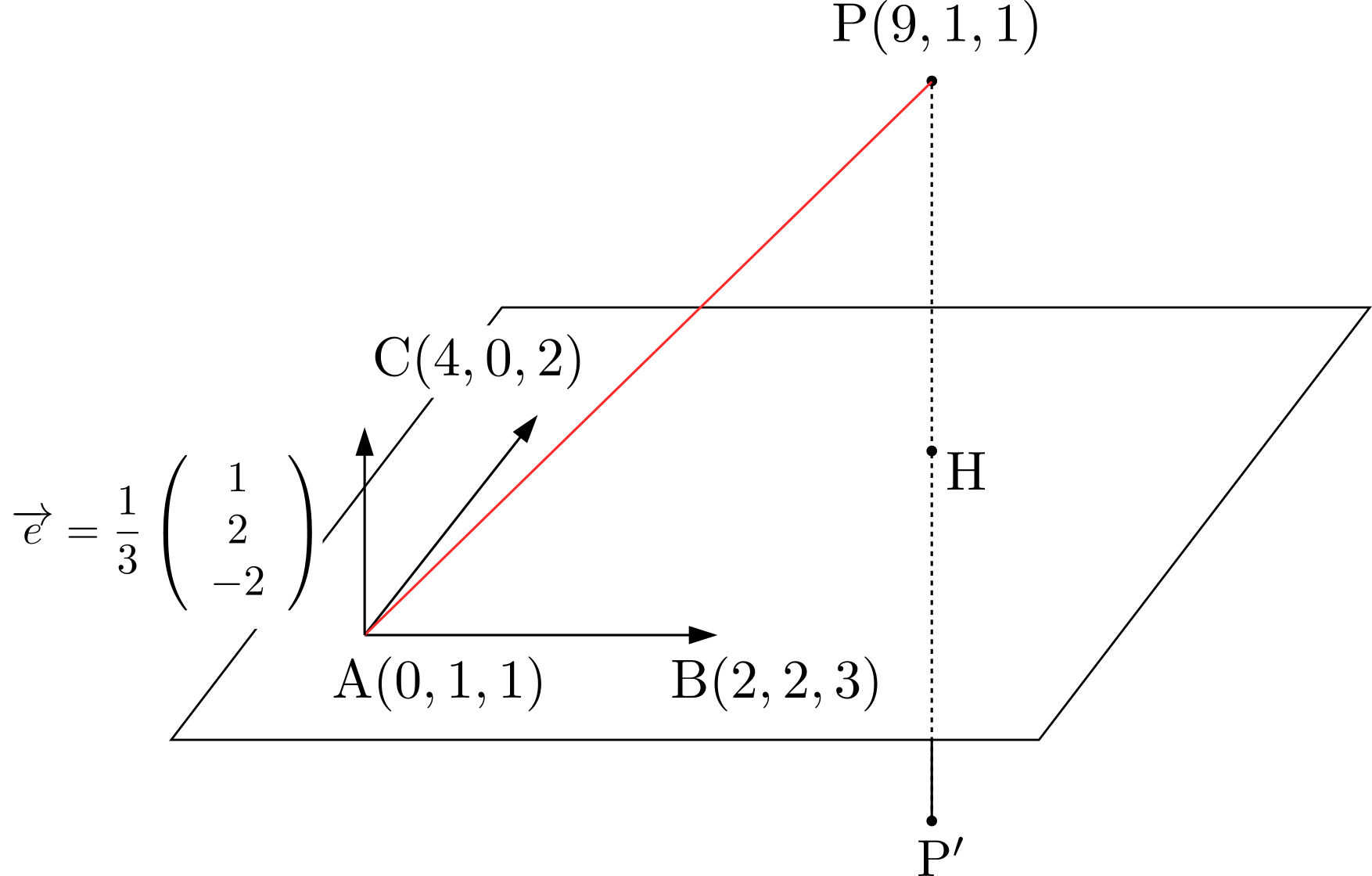
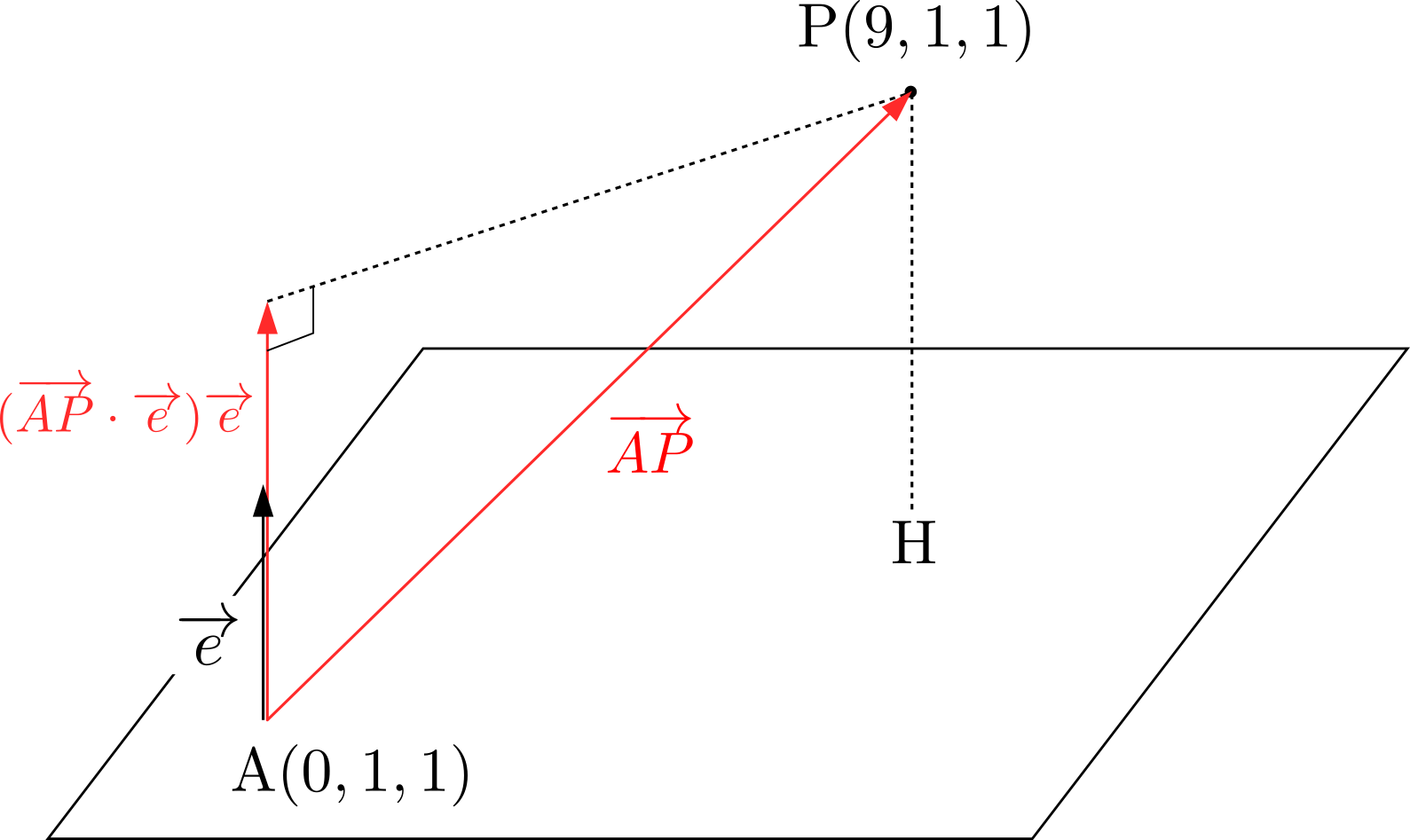
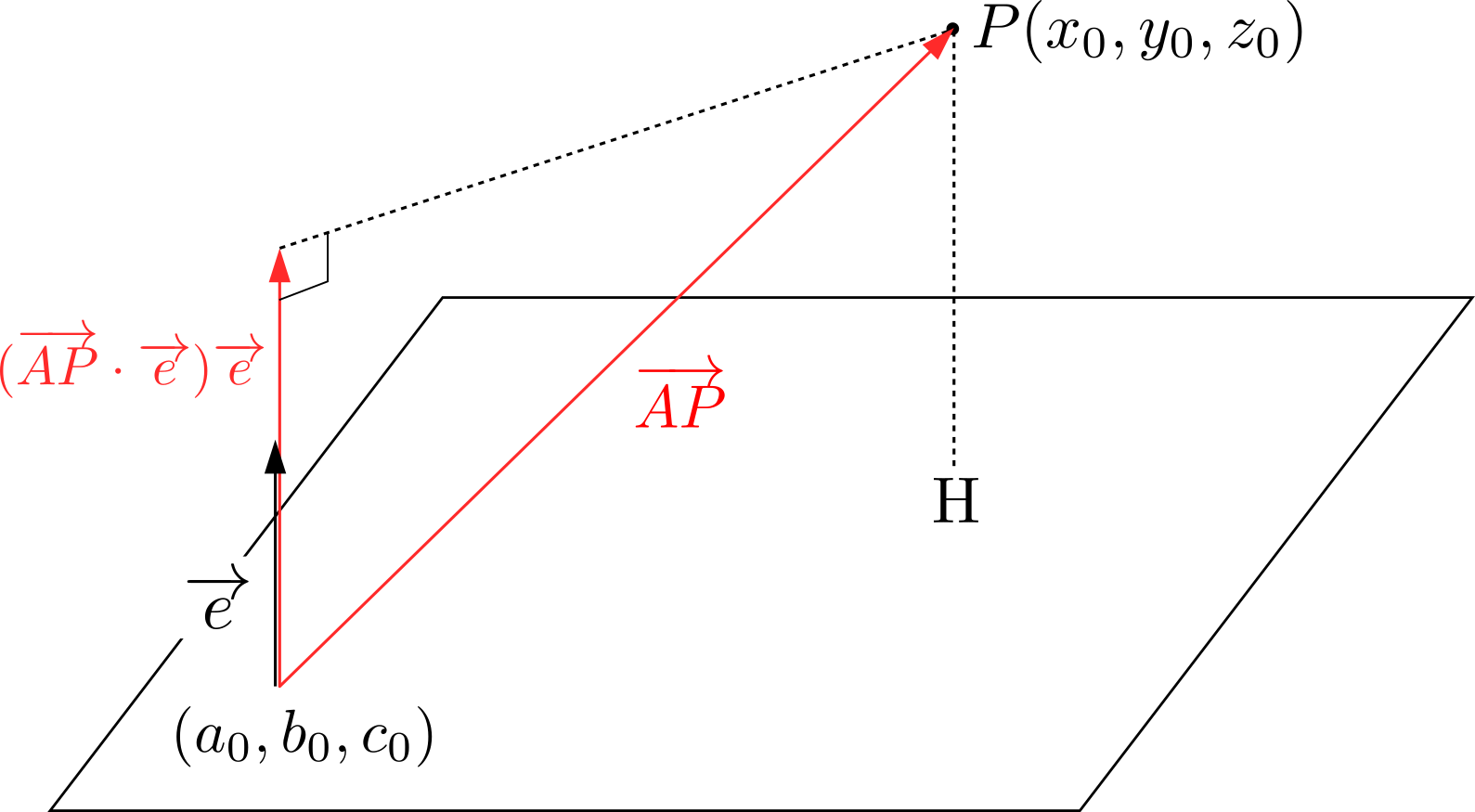 \((a_0,b_0,c_0)\)を平面上の点とする.点\(P\)から平面へおろした足を\(H\)とおけば,線分\(PH\)の長さは
\((a_0,b_0,c_0)\)を平面上の点とする.点\(P\)から平面へおろした足を\(H\)とおけば,線分\(PH\)の長さは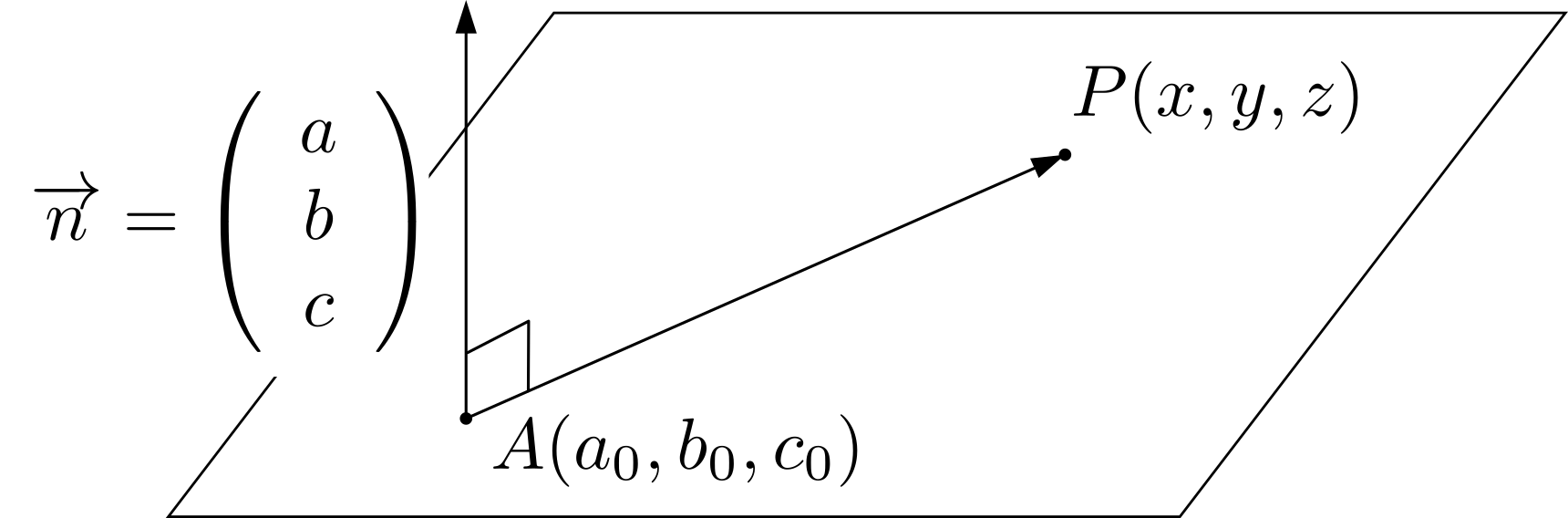 ここでは,平面はその平面の垂直方向とその平面が通る1点が定まれば決定することに着目します。平面の法線ベクトルを\(\overrightarrow{n}=(a,b,c)\),平面が通る1点の座標を\(A(a_0,b_0,c_0)\),平面上の任意の点を\(P(x,y,z)\)とおくことにします。\begin{align*}
ここでは,平面はその平面の垂直方向とその平面が通る1点が定まれば決定することに着目します。平面の法線ベクトルを\(\overrightarrow{n}=(a,b,c)\),平面が通る1点の座標を\(A(a_0,b_0,c_0)\),平面上の任意の点を\(P(x,y,z)\)とおくことにします。\begin{align*}
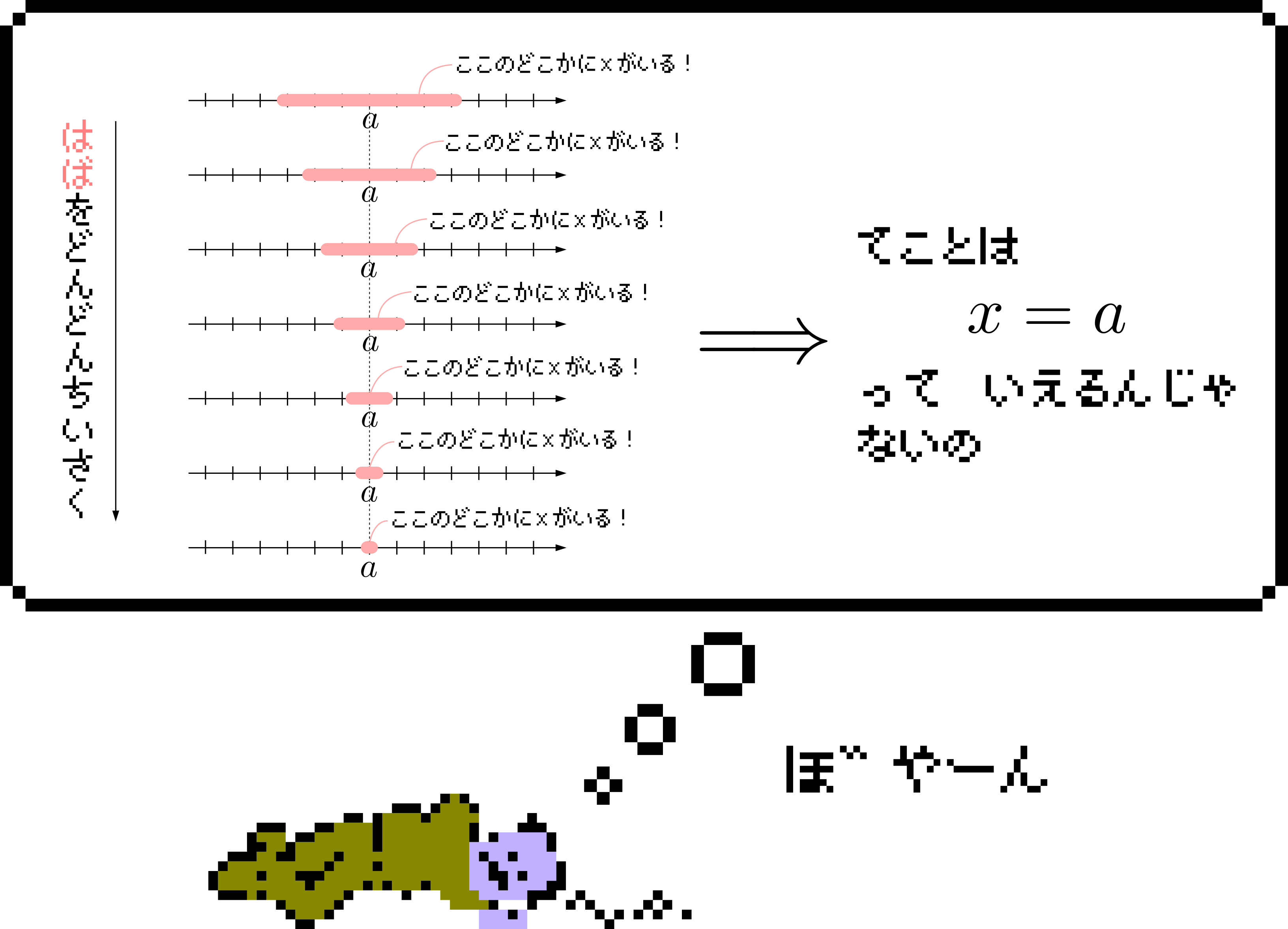
 ここで,
ここで,