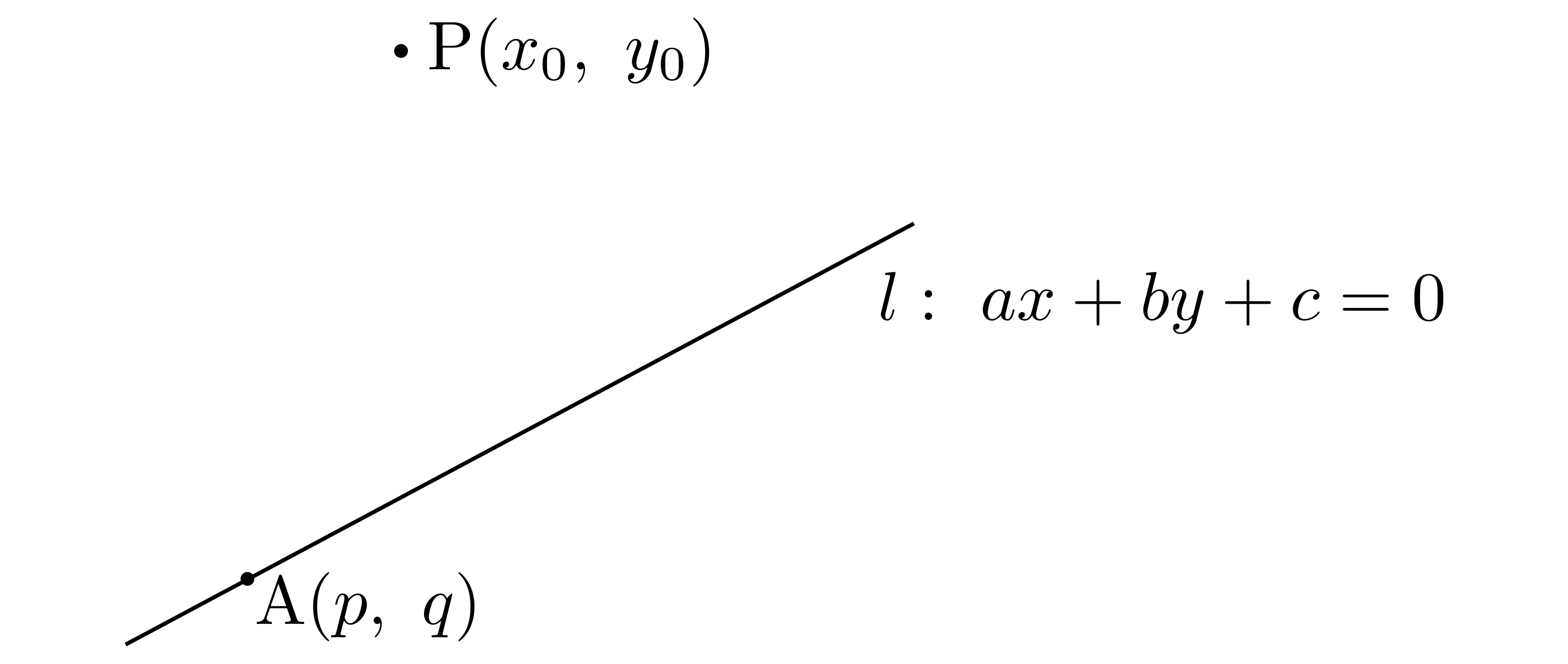数学Bで学びますが,この話題が教科書の例題や練習題に登場する際は,部分分数分解済の式が問題文中で天下りに与えれるのみで,肝心の「どう部分分数分解」するのかには全く触れていません.しかし,実戦では部分分数分解済の式が与えられることなどまずなく,自分で部分分数分解しなければなりません.そこで,ここでは「部分分数分解の仕方」について書いていきたいと思います.
・・・ところで,そもそもなぜ部分分数分解をするのでしょうか?というか,なぜ部分分数分解をしようと思うのでしょうか?方法論の前に,まずこの点にから見ていこうと思います.
少し話が飛びますが,\(\Sigma k^2\)や\(\Sigma k^3\)の公式を導出する際にどんなアイデアを使ったかを思い出しましょう.前者は\((k+1)^3-k^3=3k^2+2k+1\)という恒等式を,後者は\((k+1)^4-k^4=4k^3+6k^2+4k+1\)という恒等式を考え,\(k\)を\(1\)から\(n\)まで変えて辺々足し加えた,つまり
\[
\begin{align*}
&\sum^n_{k=1}\{ (k+1)^3-k^3\}=\sum^n_{k=1}(3k^2+2k+1)\\
&\sum^n_{k=1}\{ (k+1)^4-k^4\}=\sum^n_{k=1}(4k^3+6k^2+4k+1)
\end{align*}
\]
を計算することで例の公式\(\Sigma k^2=\frac{1}{6}n(n+1)(2n+1)\)や\(\Sigma k^3=\left\{\frac{1}{2}n(n+1)\right\}^2\)が得られたのでした.
なぜうまく計算ができて,このような公式をつくることができたのしょうか?
左辺の\(\Sigma\)のうしろ\((k+1)^3-k^3\)を見てみましょう.\(f(k)=k^3\)とおくと,\(f(k+1)=(k+1)^3\)となりますから\((k+1)^3-k^3\)は\(f(k+1)-f(k)\)と表せます.
\((k+1)^4-k^4\)についても同様に\(f(k)=k^4\)とおくと,\(f(k+1)=(k+1)^4\)となりますからやはり\((k+1)^4-k^4\)も\(f(k+1)-f(k)\)と表せます.
どうやら,「\(\Sigma\)の後ろを\(f(k+1)-f(k)\)という形にする」というところに秘密がありそうです.実際,\(\sum (f(k+1)-f(k))\)を計算してみると
\[
\begin{align*}
&\sum^n_{k=1}(f(k+1)-f(k))\\
=&(f(2)-f(1))+(f(3)-f(2))+(f(4)-f(3))+\cdots+(f(n+1)-f(n))\\
=&f(n+1)-f(1)
\end{align*}
\]
となって途中項同士が打ち消しあい,いわば「中抜け」現象がおきて生き残りが\(f(n+1)\)と\(f(1)\)だけになってくれるという,とても嬉しいことが起きます.
このように,\(\Sigma k^2\)や\(\Sigma k^3\)の公式を教科書で導出する際は\((k+1)^3-k^3=3k^2+2k+1\)や\((k+1)^4-k^4=4k^3+6k^2+4k+1\)という恒等式が天下りに与えらえていましたが,どちらも実は「\(f(k+1)-f(k)\)という形を作りたい」という積極的な動機のもとに用意する式だった,と言えます.
\(\Sigma\)計算はその背景に「\(f(k+1)-f(k)\)という形を作りたい」という気持ちがある,ということが分かりました.この点を踏まえた上で,改めて部分分数分解を眺めてみましょう.
例えば\(\sum^n_{k=1}\frac{1}{k(k+2)}\).これもやはり\(f(k+1)-f(k)\)という形を作りたいわけですから,「\(\frac{1}{k}-\frac{1}{k+2}\)と部分分数分解できたら嬉しいなあ・・・」と予想(というか願望?)します.なぜなら\(f(k)=\frac{1}{k}\)とおけば\(\frac{1}{k+2}\)は\(f(k+2)\)と表せることになり,\(f(k)-f(k+2)\)が現れるからです(\(f(k+1)-f(k)\)でなく\(f(k)-f(k+2)\)でいいの?と思った人.大丈夫,これらに本質的な違いはありません,どちらも「中抜け現象」がおきますから).
しかしあくまでこれは「予想」なので,確かめてみる必要があるわけです.予想した\(\frac{1}{k}-\frac{1}{k+2}\)を計算して\(\frac{1}{k(k+2)}\)になるか確かめてみましょう.
\[\frac{1}{k}-\frac{1}{k+2}=\frac{(k+2)-k}{k(k+2)}=\frac{2}{k(k+2)}\]
失敗しました.欲しいのは\(\frac{1}{k(k+2)}\)であって,\(\frac{2}{k(k+2)}\)ではありません.しかし,これは実りある失敗です.なぜなら,今得た式
\[\frac{1}{k}-\frac{1}{k+2}=\frac{2}{k(k+2)}\]
は,ちょっと細工すれば,すなわち両辺を2で割ってやれば,
\[
\begin{align*}
&\frac{1}{k}-\frac{1}{k+2}\times\frac{1}{2}=\frac{2}{k(k+2)}\times\frac{1}{2}\\
&\frac{1}{k(k+2)}=\frac{1}{2}\left(\frac{1}{k}-\frac{1}{k+2}\right)
\end{align*}
\]
が得られます.\(\frac{1}{2}\)がついているものの,ちゃんと\(f(k)-f(k+2)\)という形になっています.これならうまくいきそうです.
このように,部分分数分解は,「\(f(k+1)-f(k)\)のような形を作りたい」という動機がまず最初にあり,その気持ちから然るべき予想をし,「予想を計算,その結果をあとで微調整」と考えるのが肝というわけです.
練習問題
\(S_n=\sum^{n}_{k=1}a_k\)とする.このとき,
\[\sum^n_{k=1}\frac{a_{k+1}+a_{k+2}}{S_kS_{k+1}S_{k+2}}\]を\(S_1,~S_2,~S_{n+1},~S_{n+2}\)で表せ.
\(\sum\)のうしろを\(f(k+1)-f(k)\)や\(f(k+2)-f(k)\)のような形にしたいという気持ちから,\(\frac{a_{k+1}+a_{k+2}}{S_kS_{k+1}S_{k+2}}=\frac{1}{S_{k+2}S_{k+1}}-\frac{1}{S_{k+1}S_{k}}\)ではないか?と予想します(\(f(k)=\frac{1}{S_{k+1}S_{k}}\)とおくと\(f(k+1)=\frac{1}{S_{k+2}S_{k+1}}\)となって\(f(k+1)-f(k)\)という形が現れますから).
この予想が正しいか,計算して確認してみます.
\[
\begin{align*}
&\frac{1}{S_{k+2}S_{k+1}}-\frac{1}{S_{k+1}S_{k}}=\frac{S_{k}-S_{k+2}}{S_kS_{k+1}S_{k+2}}\\
=&\frac{(a_1+a_2+\cdots+a_k)-(a_1+a_2+\cdots+a_k+a_{k+1}+a_{k+2})}{S_kS_{k+1}S_{k+2}}\\
=&-\frac{a_{k+2}+a_{k+1}}{S_kS_{k+1}S_{k+2}}
\end{align*}
\]
すなわち
\[\frac{1}{S_{k+2}S_{k+1}}-\frac{1}{S_{k+1}S_{k}}=-\frac{a_{k+2}+a_{k+1}}{S_kS_{k+1}S_{k+2}}\]
を得ます.\(-\)(マイナス)が邪魔ですね.両辺に\(-1\)を掛けて微調整しましょう.
\[\frac{a_{k+2}+a_{k+1}}{S_kS_{k+1}S_{k+2}}=\frac{1}{S_{k+1}S_{k}}-\frac{1}{S_{k+2}S_{k+1}}\]
よって,
\[\sum^{n}_{k=1}\frac{a_{k+2}+a_{k+1}}{S_kS_{k+1}S_{k+2}}=\sum^{n}_{k=1}\left(\frac{1}{S_{k+1}S_{k}}-\frac{1}{S_{k+2}S_{k+1}}\right)\]
「\(f(k)-f(k+1)\)」という形が作れたので,これでうまく「中抜け現象」を作り出せそうですね(以下解答は割愛).
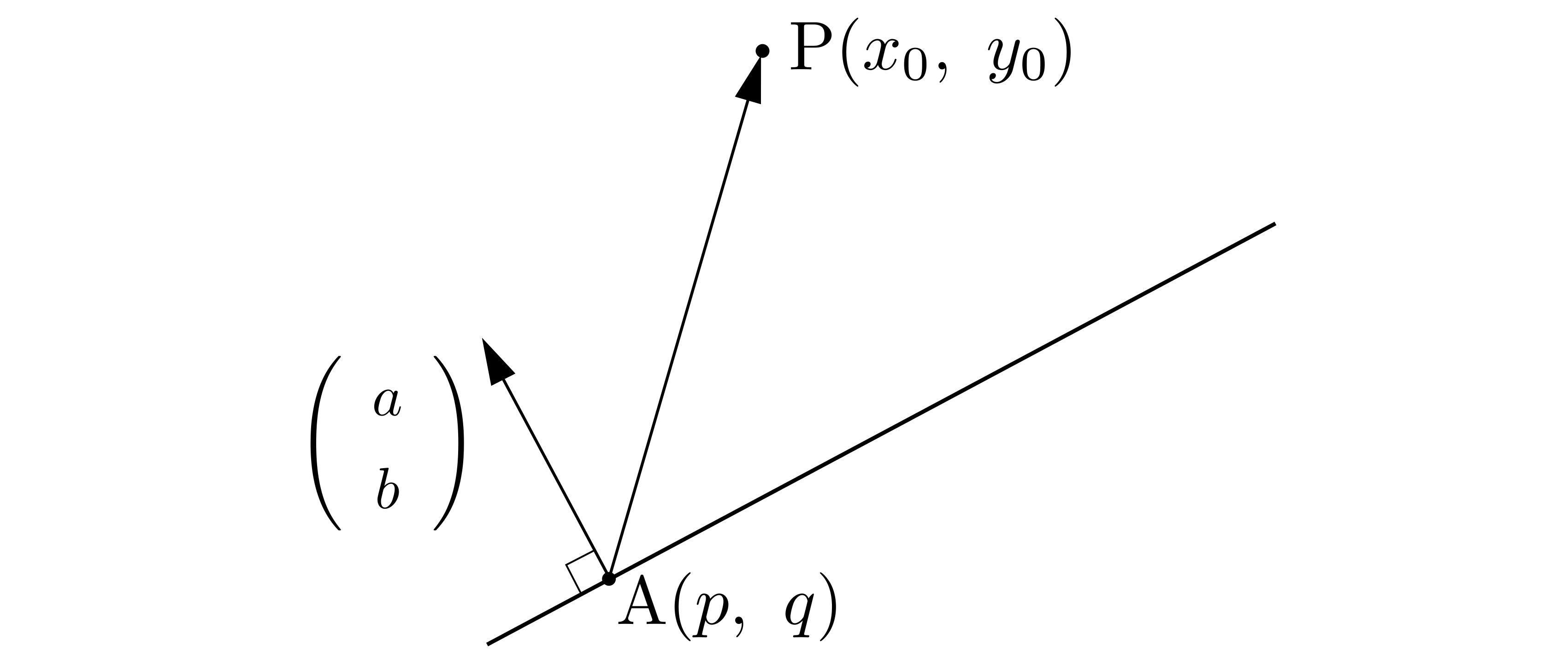
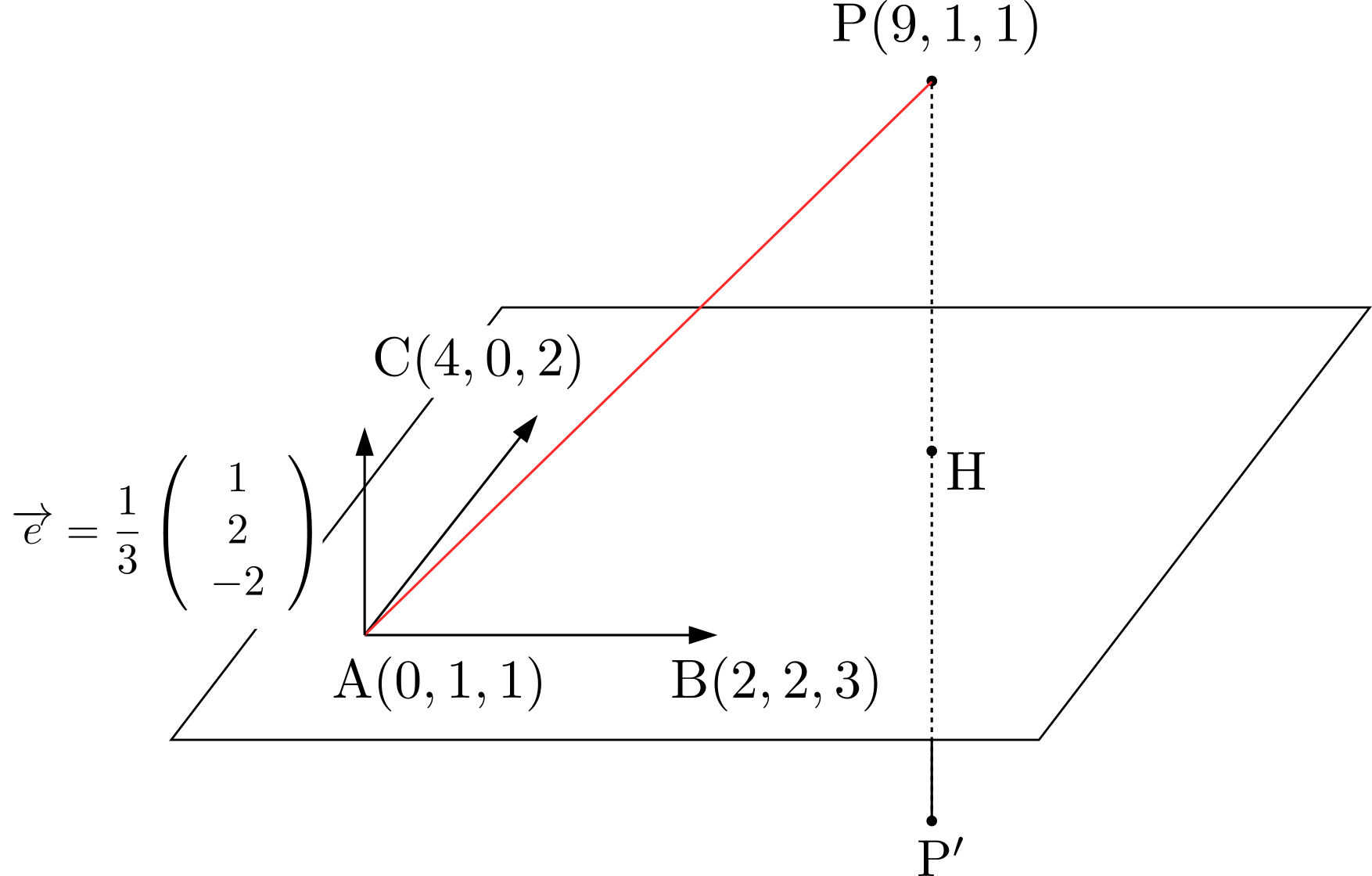 位置ベクトルの定義により,空間上の座標\(P’\)とベクトル\(\overrightarrow{OP’}\)の成分は1対1に対応してますから,\(\overrightarrow{OP’}\)を求まるということそれは空間上の座標\(P’\)が求まることに等しい.そこで\(\overrightarrow{OP’}\)を求めることにします.点\(P\)から平面上に下した垂線の足の座標を\(H\)とおけば,\(\overrightarrow{OP’}=\overrightarrow{OP}+2\overrightarrow{PH}\)とできます.\(\overrightarrow{PH}\)を求めます.
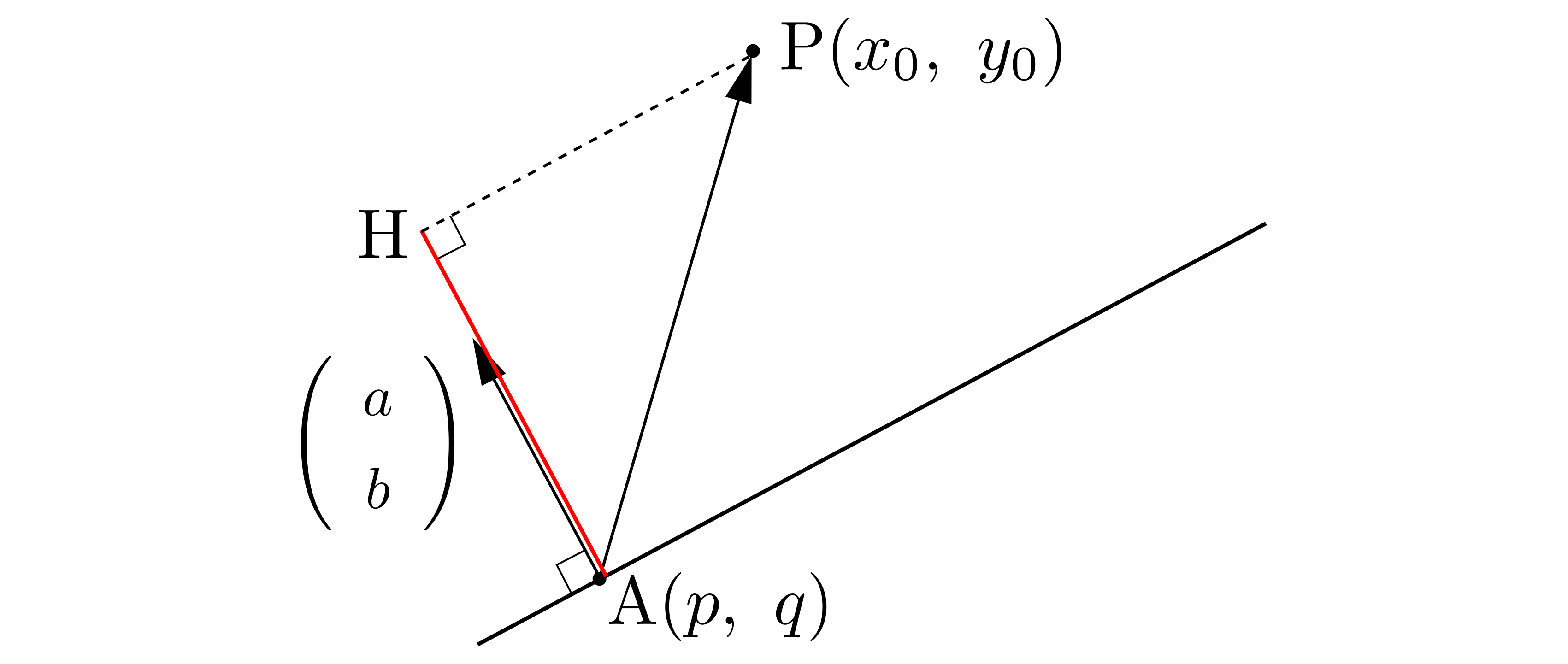
位置ベクトルの定義により,空間上の座標\(P’\)とベクトル\(\overrightarrow{OP’}\)の成分は1対1に対応してますから,\(\overrightarrow{OP’}\)を求まるということそれは空間上の座標\(P’\)が求まることに等しい.そこで\(\overrightarrow{OP’}\)を求めることにします.点\(P\)から平面上に下した垂線の足の座標を\(H\)とおけば,\(\overrightarrow{OP’}=\overrightarrow{OP}+2\overrightarrow{PH}\)とできます.\(\overrightarrow{PH}\)を求めます.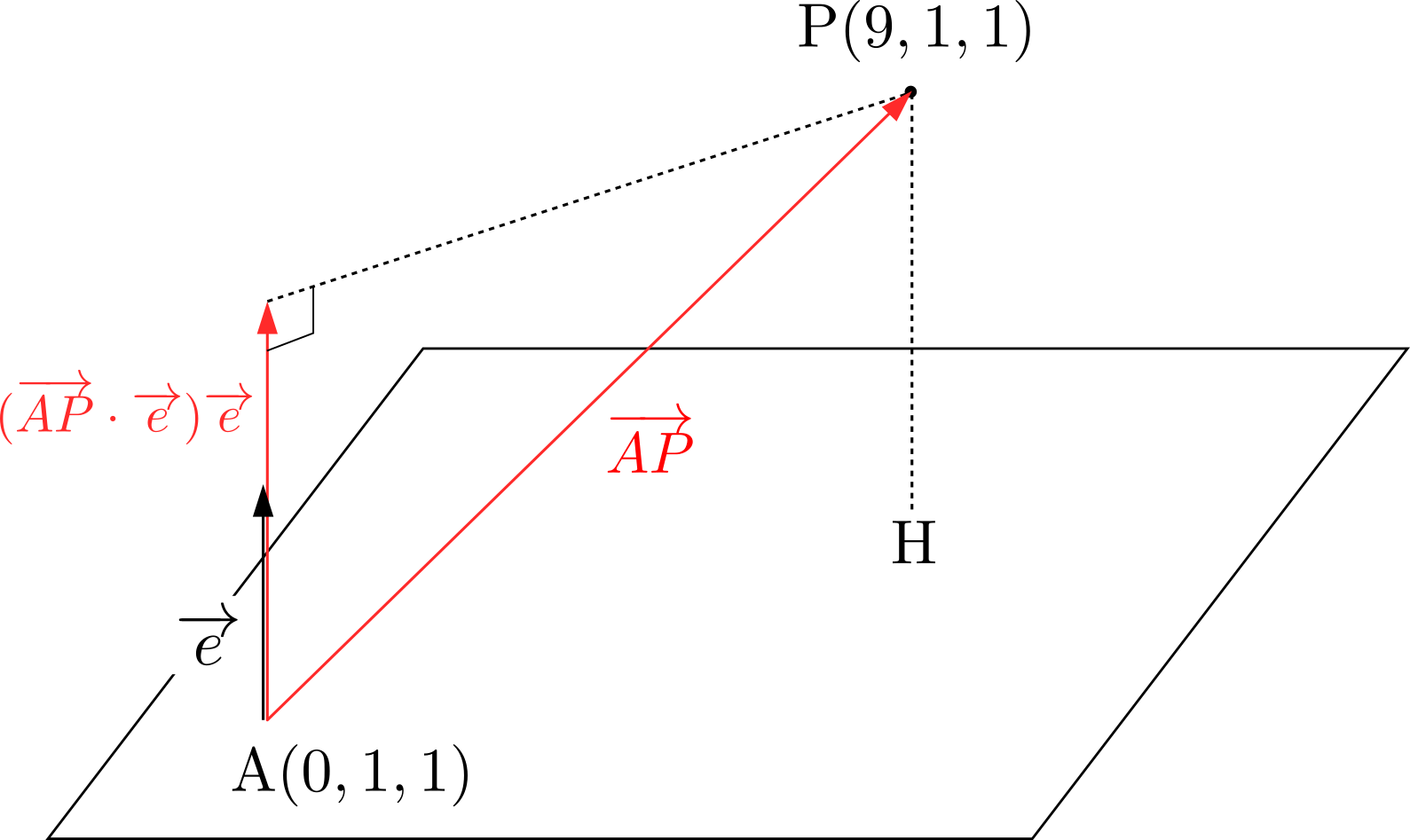 ここで,正射影ベクトル\((\overrightarrow{AP}\cdot\overrightarrow{e})\overrightarrow{e}\)は\(\overrightarrow{HP}\)に等しい(\(\overrightarrow{e}\)は平面に垂直な単位ベクトル,外積によって直ちに求まる).したがって\begin{align*}
ここで,正射影ベクトル\((\overrightarrow{AP}\cdot\overrightarrow{e})\overrightarrow{e}\)は\(\overrightarrow{HP}\)に等しい(\(\overrightarrow{e}\)は平面に垂直な単位ベクトル,外積によって直ちに求まる).したがって\begin{align*}

 と考えることで
と考えることで

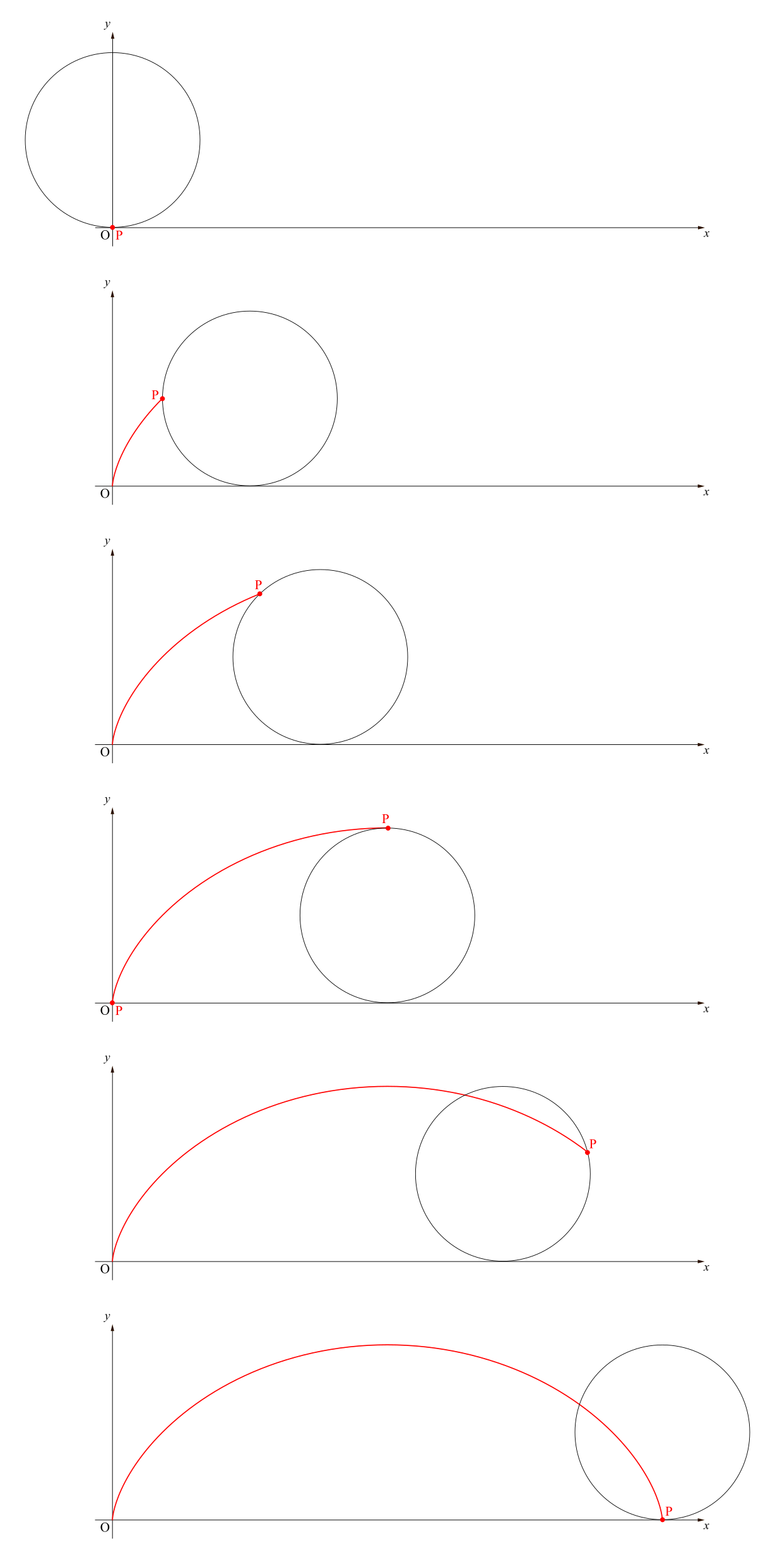
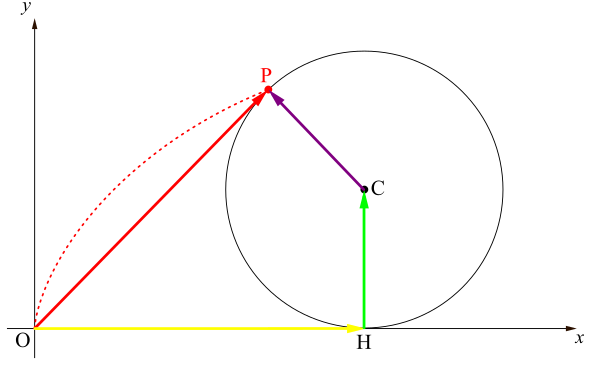
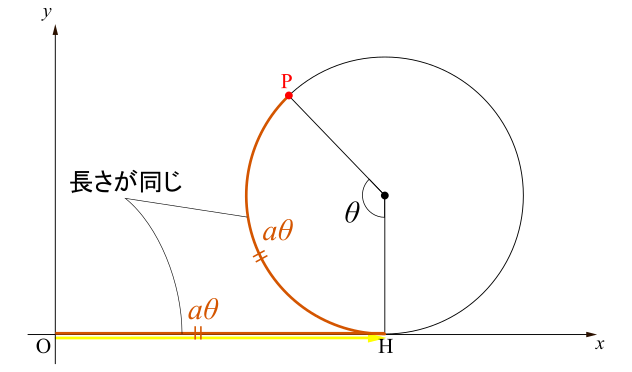 このベクトルは始点が既に原点にありますから,位置ベクトル,すなわちその成分と終点が指し示す座標が一致しているはずです.したがって\(\overrightarrow{\mathrm{OH}}\)の終点が指し示す座標を調べればよい.\(\mathrm{OH}=\text{孤}\mathrm{PH}\)であることに注意すると(「滑らずに」転がしたんだから!右図参照),\(\mathrm{OH}=a\theta\).したがって点\(\mathrm{H}\)の座標は\((a\theta,0)\)で,(座標と成分が対応するから)\(\overrightarrow{\mathrm{OH}}\)の成分は\(\left(\begin{array}{c} a\theta \\ 0 \\ \end{array} \right)\)となります.
このベクトルは始点が既に原点にありますから,位置ベクトル,すなわちその成分と終点が指し示す座標が一致しているはずです.したがって\(\overrightarrow{\mathrm{OH}}\)の終点が指し示す座標を調べればよい.\(\mathrm{OH}=\text{孤}\mathrm{PH}\)であることに注意すると(「滑らずに」転がしたんだから!右図参照),\(\mathrm{OH}=a\theta\).したがって点\(\mathrm{H}\)の座標は\((a\theta,0)\)で,(座標と成分が対応するから)\(\overrightarrow{\mathrm{OH}}\)の成分は\(\left(\begin{array}{c} a\theta \\ 0 \\ \end{array} \right)\)となります.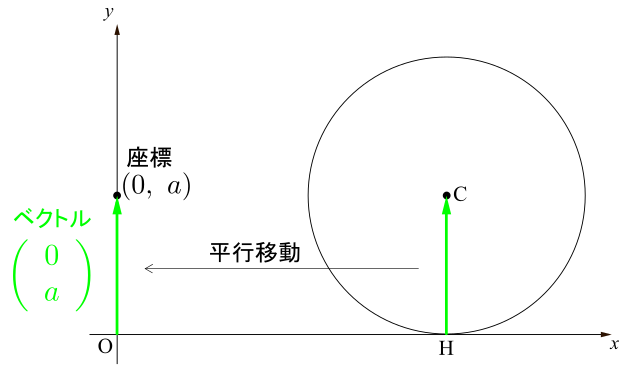 始点が原点にあれば,そのまま終点が指し示す座標を読めばいいのですが,これは始点は原点ではありませんね.しかしベクトルは向きと大きささえ変えさえしなければ自由に動かせるのでしたから,始点を原点にとってから,その終点の座標を読めばよいでしょう.始点を原点にとったときのベクトルの終点が指し示す座標は\((0,~a)\)ですから,そのベクトルの成分は\(\overrightarrow{\mathrm{OH}}\)の成分は\(\left(\begin{array}{c} 0 \\ a \\ \end{array} \right)\)となります.
始点が原点にあれば,そのまま終点が指し示す座標を読めばいいのですが,これは始点は原点ではありませんね.しかしベクトルは向きと大きささえ変えさえしなければ自由に動かせるのでしたから,始点を原点にとってから,その終点の座標を読めばよいでしょう.始点を原点にとったときのベクトルの終点が指し示す座標は\((0,~a)\)ですから,そのベクトルの成分は\(\overrightarrow{\mathrm{OH}}\)の成分は\(\left(\begin{array}{c} 0 \\ a \\ \end{array} \right)\)となります.